距離空間の完備化を丁寧に筋よく
$(X,d),(Y,d')$を距離空間とする.写像$f:(X,d)\to (Y,d')$が等長であるとは任意の$x,y\in X$に対して$d'(f(x),f(y))=d(x,y)$が成り立つときをいう.
等長写像$f:X\to Y$はうめこみである.つまり$f$は単射かつ連続であって$X$の位相がちょうど$Y$の位相の$f$による引き戻しに合致する.
$X,Y$を距離空間,$f:X\to Y$をその間の写像とする.$Y$が$f$に関する$X$の完備化であるとは以下の3条件を満たすことをいう:
(1) $f$は等長.
(2) $\overline{f(X)}=Y$,すなわち$X$の像$f(X)$が$Y$で稠密
(今$Y$は距離空間であるからこれは「任意の$y\in Y$に対してある$X$内の点列$\{a_n\}_{n\geq 1}$が存在して$\displaystyle Y\mbox{-}\lim_{n\to \infty} f(a_n)=y$」と言い換えられる（ここで$Y\mbox{-}\lim$は$Y$（の位相）における極限であることを強調した記法).
(3) $Y$は完備.
$(X,d)$を距離空間とする.$X$のCauchy列全体の集合を$ X^{\N}_{\rm{Cauchy}}$と書くことにし，その上の同値関係$\sim$を
$$\left\{x_n\right\}_{n\geq 1}
\sim \left\{y_n\right\}_{n\geq 1}
\iff d(x_n,y_n)\to 0$$によって定め，$\hat{X}:= X^{\N}_{\rm{Cauchy}}/\sim$とおく.以下$\{x_n\}_{n\geq 1}\in X^{\N}_{\rm{Cauchy}}$の同値類を$[\{x_n\}_{n\geq 1}]\in\hat{X}$で表す.
次に$\hat{X}$上の距離関数$\hat{d}$を以下のように定める:
$$\hat{d}([\{x_n\}_{n\geq 1}],[\{y_n\}_{n\geq 1}])
:=\lim_{n\to \infty}d(x_n,y_n).$$($\hat{d}$のwell-defined性は容易に確かめられる （下に書く）.)
ここで$X$を定数列に対応させる写像$\iota \colon X\to \hat{X};x\mapsto [\left\{x\right\}_{n\geq 1}]$によって$\hat{X}$に埋め込む（$\left\{x\right\}_{n\geq 1}$は$x$がずっと並ぶ定数列$x,x,x,\ldots$である。これはもちろんCauchy列なのでこの写像はwell-defined）.
このとき$(\hat{X},\hat{d})$は$\iota$に関する$(X,d)$の完備化である.
任意の$\left\{x_n\right\}_{n\geq 1}, \left\{y_n\right\}_{n\geq 1}\in X^{\N}_{\rm{Cauchy}}$に対して$\left\{d(x_n,y_n)\right\}_{n\geq 1}$はCauchy列であることは容易にわかるから$\mathbb{R}$の完備性よりこれは収束する.
また$\left\{x_n\right\}_{n\geq 1}\sim \left\{x'_n\right\}_{n\geq 1},\left\{y_n\right\}_{n\geq 1}\sim \left\{y'_n\right\}_{n\geq 1}$ならば
$$\displaystyle\lim_{n\to \infty}d(x_n,y_n)=\displaystyle\lim_{n\to \infty}d(x'_n,y'_n)$$であることも簡単にわかる（実際三角不等式$d(x_n,y_n)\leq d(x_n,x'_n)+d(x'_n,y'_n)+d(y'_n,y_n)$より直ちにわかる）.
上の赤字部分は構成法とともに覚えておくことが非常に大事である（本によっては$\hat{d}$の構成をステートメントに明記していないものがあるが良くない）．例えば整数論においてp進体の理論を扱うときには必要になってくる．
まず次を示そう。
任意の$\hat{x}:=[\left\{x_n\right\}_{n\geq 1}]\in \hat{X}$をとる.
このとき定数列$a_{m}:=\iota(x_m)(=[\left\{x_m\right\}_{n\geq 1}])$は$a_{m}\to \hat{x}$となる。即ち$\lim_{m\to \infty}\hat{d}(a_{m},\hat{x})=0$を満たす．
$$\lim_{m\to \infty}\hat{d}(a_{m},\hat{x}) =\lim_{m\to \infty}\hat{d}([\left\{x_m\right\}_{n\geq 1}],[\left\{x_n\right\}_{n\geq 1}]) =\lim_{m\to \infty}\left(\lim_{n\to \infty}d(x_m,x_n)\right) =0$$ となるので示される.ここで2番目のイコールは$\hat{d}$の定義から[^3]、その次のイコールは$\{x_n\}_{n\geq 1}$がCauchy列であることより。
つまり$[x_1,x_1,x_1,\cdots], [x_2,x_2,x_2,\cdots], [x_3,x_3,x_3,\cdots], \cdots$という（$\iota(X)\subset\hat{X}$内の）点列は$[x_1,x_2,x_3,\cdots]$という点に収束するのである。
さて本題の証明に入ろう：
さて完備化の定義を思い出すと(1)写像$\iota$の等長性、(2)像の稠密性、(3)$\hat{X}$の完備性の三つを示せば良い。以下それを順にやっていこう：
(1) ($\iota$の等長性)
$\hat{d}$の定義から
$$\hat{d}(\iota(x),\iota(y))=\lim_{n\to \infty}d(x,y)=d(x,y).$$よって$\iota$は等長.
(2) (像$\iota(X)$の$\hat{X}$における稠密性)
これは上の命題から直ちに従う。
(3)($(\hat{X},\hat{d})$の完備性)
$\hat{X}$内の任意のCauchy列$\left\{\hat{x}_n\right\}_{n\geq 1}$をとる.
(2)より各$\hat{x}_n\in \hat{X}$に対して$\hat{d}(\iota(k_n),\hat{x}_n)<1/n$を満たす$k_n\in X$が取れる（すると$\lim_{n\to\infty} \hat{d}(\iota(k_n),\hat{x}_n)=0$が成り立つ）.ここで$X$内の点列$\left\{k_n\right\}_{n\geq 1}$はCauchy列である.
(実際(1)に気を付ければ, 三角不等式より$$d(k_m,k_n)=\hat{d}(\iota(k_m),\iota(k_n))
\leq \hat{d}(\iota(k_m),\hat{x}_m)+\hat{d}(\hat{x}_m,\hat{x}_n)+\hat{d}(\hat{x}_n,\iota(k_n))
\to 0\ (m,n\to \infty).)$$よって$\hat{k}:=[\left\{k_n\right\}_{n\geq 1}]\in \hat{X}$を取ることが出来る.
このとき($\hat{X}$において) $\hat{x}_m\to \hat{k}$が成り立つ． (実際三角不等式より，$$\hat{d}(\hat{x}_m,\hat{k}) \leq \hat{d}(\hat{x}_m,\iota(k_m))+\hat{d}(\iota(k_m),\hat{k}) =\hat{d}(\hat{x}_m,\iota(k_m))+\lim_{n\to \infty} d(k_m,k_n) \to 0\ (m\to \infty).)$$ これで証明完了である.
これで任意の距離空間がある完備距離空間の中に埋め込めることがわかった.そしてその作り方は$X$のCauchy列のグループ一つ一つを数とみなし，かつもとの$X$の数$x$はそれによる定数列$x,x,x,\ldots$のグループを$x$と同一視することで$X$の数を拡張するのである．
ここで良く使われる事実を補題として挙げておく。
上の定理の状況を考える。$\hat{X}$において$\iota(a_n)\to \hat{x},\iota(b_n)\to \hat{y} \ (n\to \infty)$であるとする。このとき
$$\hat{d}(\hat{x},\hat{y})
=\lim_{n\to \infty} d(a_n,b_n).$$
$$\begin{eqnarray} |\hat{d}(\hat{x},\hat{y})-\hat{d}(\iota(a_n),\iota(b_n))| =&|\hat{d}(\hat{x},\hat{y})-\hat{d}(\hat{x},\iota(b_n))+\hat{d}(\hat{x},\iota(b_n))-\hat{d}(\iota(a_n),\iota(b_n))|\\ \leq &\hat{d}(\hat{y},\iota(b_n))+\hat{d}(\hat{x},\iota(a_n))\\ \to &0\quad (n\to \infty)\end{eqnarray}$$
であるから $$\hat{d}(\hat{x},\hat{y})=\lim_{n\to \infty} \hat{d}(\iota(a_n),\iota(b_n)) =\lim_{n\to \infty} d(a_n,b_n).$$
次にそのような完備距離空間はある意味で一意的に定まることを見よう.
$(X,d)$を距離空間とする.$(\hat{X},\hat{d})$を$\iota$に関する$(X,d)$の完備化,$(\hat{X}',\hat{d}')$を$\iota'$に関する$(X,d)$の完備化とすると,ある全射等長写像$f:\hat{X}\to \hat{X}'$が存在して以下を可換にする.
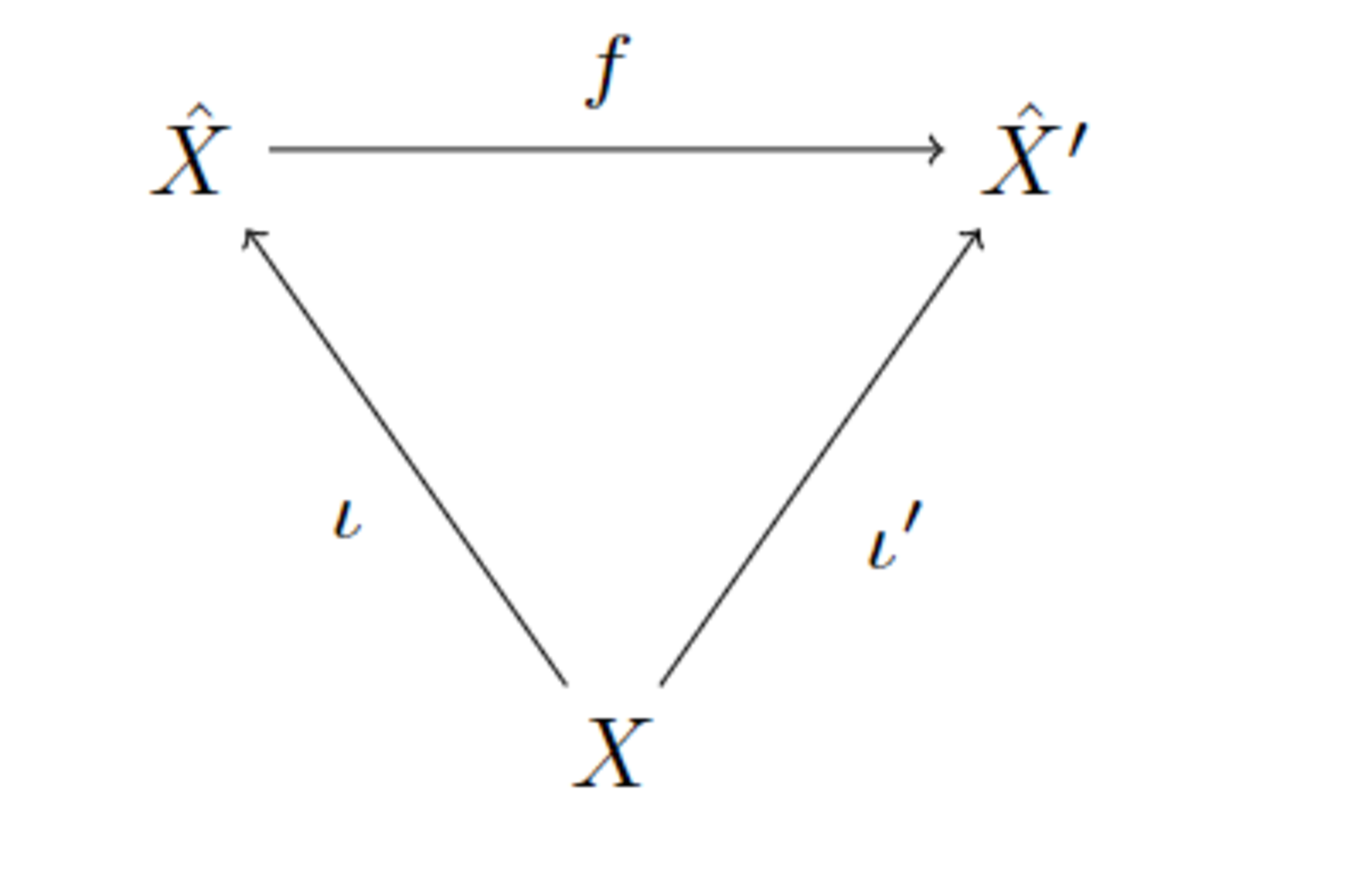picture
準備中（たしか松坂位相に載っていた）.
おわりです．
[^3]: 第三項の$x_m$は$x_m,x_m,x_m,\cdots$という定数列の第$n$項であり, $x_n$は$x_1,x_2,x_3,\cdots$という列の第$n$項である.
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
