めも　2022-07-16.

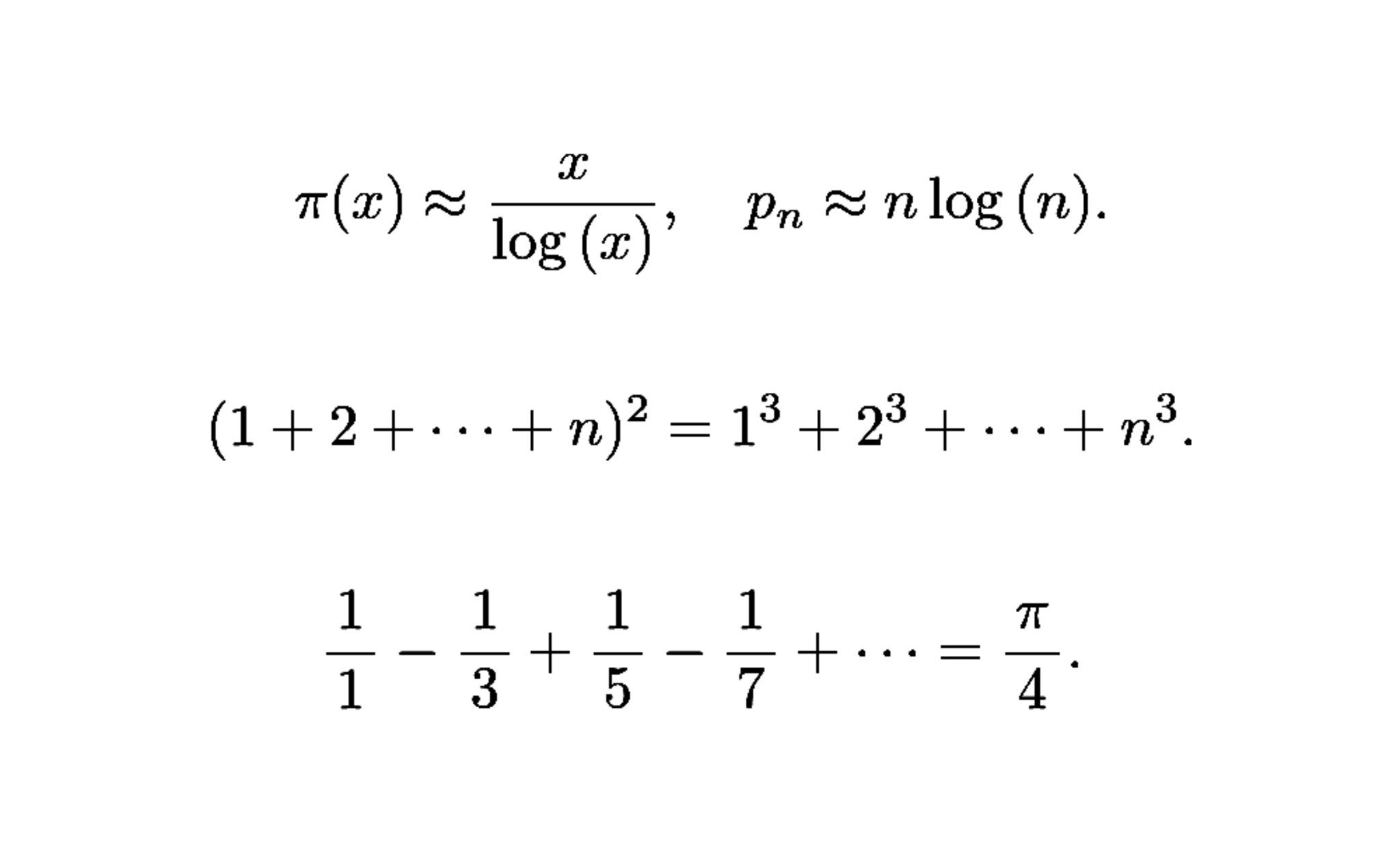めも
$\ $
$\ $
$\ $
$\ $
$\ $
$\ $

素数定理ノ直観的釈義

整数$n$充分ニ大ナリトス
先有名ノ Legendre ノ定理ニ依テ
\begin{align} v_p(n!)=\sum_{e\geqslant1}\left\lfloor\frac{\,n\,}{\,p^e\,}\right\rfloor\approx\frac{n}{p-1}, \end{align}
而
\begin{align} n!&\approx\prod_{p\leqslant n}p^{n/(p-1)},\\ \log{(n!)}&\approx n\sum_{p\leqslant n}\frac{\log{(p)}}{p-1}. \end{align}
又別ニ
\begin{align} \log{(n!)}\approx n\left(\log{(n)}-1\right). \end{align}
由テ
\begin{align} \sum_{p\leqslant n}\frac{\log{(p)}}{p-1}\approx\log{(n)}-1. \end{align}
($\longrightarrow$ Mertens ノ第一定理)
$\ $
$\ $
$\ $
$\varepsilon(n)=\begin{cases}1\ \ \ (n\in\mathrm{primus})\\0\ \ \ (n\not\in\mathrm{primus})\end{cases}$ヲ用ヰテ　上式各辺ノ差分 ($n\longmapsto n-1$) ヲ較ブルニ
\begin{align} \varepsilon(n)\frac{\log{(n)}}{n-1}&\approx\frac{1}{n-1},\\ \varepsilon(n)&\approx\frac{1}{\log{(n)}}. \end{align}
凡ソ$\varepsilon(n)\approx\pi(n)/n$ノ関係成立スベキヿヲ容認セバ
\begin{align} \pi(n)\approx\frac{n}{\log{(n)}} \end{align}
ノ近似ヲ得ベシ
$\ $
$\ $
$\ $
是故ニ$p_n\approx n\log{(n)}$亦成立ス
$\ $
$\ $
$\ $
上記ハ但ダ近似ノ発想ニ基テ直覚的概算ヲ論ゼルノミニシテ　厳密ノ証明トハ手法ヲ異トシタルヿ　誤解有ルベカラズ
$\ $
$\ $
$\ $
$\ $
$\ $
$\ $

三乗和公式ト一乗和公式トノ関係

正整数$n$ニ於テ
\begin{align} (1+2+\cdots+n)^2=1^3+2^3+\cdots+n^3 \end{align}
即$\sum k^3=(\sum k)^2$ノ等式成立スルハ甚ダ有名ノ事実ナレドモ別ニ下記ノ如計算ニ依テ証明スルモ亦可能ナリ
$\ $
$\ $
$\ $
\begin{align} \sum_{0\leqslant k\leqslant n}^k(k+1)k^2&=\sum_{\substack{0\leqslant i,j\\i+j\leqslant n}}^{i,j}(i+j)^2\qquad(k=i+j)\\ &=2\sum_{\substack{0\leqslant i,j\\i+j\leqslant n}}^{i,j}i(i+j)\\ &=2\sum_{0\leqslant i\leqslant k\leqslant n}^{i,k}ik\\ &=\left[\sum_{0\leqslant i\leqslant k\leqslant n}^{i,k}+\sum_{0\leqslant k\leqslant i\leqslant n}^{i,k}\right]ik\\ &=\sum_{\substack{0\leqslant i\leqslant n\\0\leqslant k\leqslant n}}^{i,k}ik+\sum_{0\leqslant k\leqslant n}^kk^2\\ &=\left[\sum_{0\leqslant k\leqslant n}^kk\right]^2+\sum_{0\leqslant k\leqslant n}^kk^2. \end{align}
$\ $
$\ $
$\ $
$\ $
$\ $
$\ $

Leibniz 級数ノ数論的計算法

正ナル整数$n$ニ対シテ方程式$n=x^2+y^2$即
\begin{align} n=(x+y\sqrt{-1})(x-y\sqrt{-1}) \end{align}
ノ整数解$(x,y)$ノ総数ヲ$r_2(n)$ニ表サムトス

先$r_2(n)$ヲ$4$ニ依除シテ$r(n)=r_2(n)/4$トシ単数倍ノ相異ヲ度外視ス　其寸素元ハ$\{x+y\sqrt{-1}\mid x>0,\ |x|\geqslant|y|\}$ニ限リテ解釈スベク又特別ニ整数$2$ノ分解ハ$(1+\sqrt{-1})^2$ヲ正規トスベシ

複素整数環ニ於ル整数ノ分解ノ事ニ依レバ
\begin{align} r(p^e)&=\begin{cases}1&(p=2)\\&\\e+1&(p\equiv1\ \ (\mathrm{mod}.4))\\&\\\!\!\!\begin{cases}0&(2\nmid e)\\1&(2\mid e)\end{cases}&(p\equiv3\ \ (\mathrm{mod}.4))\end{cases}\\ &\\ &=\chi(1)+\chi(p)+\cdot+\chi(p^e). \end{align}
但
\begin{align} \chi(n)=\begin{cases}0&(n\equiv0\ \ (\mathrm{mod}.2))\\+1&(n\equiv1\ \ (\mathrm{mod}.4))\\-1&(n\equiv3\ \ (\mathrm{mod}.4))\end{cases}. \end{align}
又
\begin{align} \gcd(m,n)=1\;\Longrightarrow\;\left(\begin{array}{l}r(mn)=r(m)r(n)\\\chi(mn)=\chi(m)\chi(n)\end{array}\right.. \end{align}
是故ニ
\begin{align} r(n)=\sum_{d\mid n}\chi(d). \end{align}
$\ $
$\ $
$\ $
半径$\sqrt{N}$ノ円ノ面積ヨリ下式ヲ知ルベシ
\begin{align} \pi&=\lim_{N\to\infty}\frac{1}{N}\sum_{n=0}^{n=N}r_2(n)=\lim_{N\to\infty}\frac{1}{N}\sum_{n=1}^{n=N}r_2(n)\\ &=\lim_{N\to\infty}\frac{4}{N}\sum_{n=1}^{n=N}\sum_{d\mid n}\chi(d)\\ &=\lim_{N\to\infty}\frac{4}{N}\sum_{d=1}^{d=N}\sum_{\substack{n=1\\d\mid n}}^{n=N}\chi(d)\\ &=\lim_{N\to\infty}\frac{4}{N}\sum_{d=1}^{d=N}\left\lfloor\frac{\,N\,}{\,d\,}\right\rfloor\chi(d)\\ &\stackrel{\ast1}{=}\sum_{d=1}^{\infty}4\cdot\frac{\chi(d)}{d}\\ &=\sum_{d=1}^{\infty}4\cdot\frac{(-1)^{d-1}}{2d-1}. \end{align}
斯ノ如クセバ$\frac{\,1\,}{\,1\,}-\frac{\,1\,}{\,3\,}+\frac{\,1\,}{\,5\,}-\frac{\,1\,}{\,7\,}+\cdots$ノ収束値ニ円周率$\pi$ノ現ルベキヿ明快ナリ

$\ast1$　此操作ハ厳密ニ非ズ
$\ $
$\ $
$\ $
$\ $
$\ $
$\ $