数学オリンピック体験記

IMO2022が終わり自分は数オリに選手として参加する事はもう無いのでこれまでの事を振り返りたいと思います. 一数オリerとしての意見なので強い主張があってもそういうものとして受け止めてください()

中三(JJMO2020)までのダイジェスト

数オリと出会ったのは中一だと思いますが実力が無いので受けるに値しないと思い初めてJJMOを受けたのは中二です。今思えば中一の時も受けとくべきでした(モチベーションになるので)

中二のときJJMOを受けて運良く本選に出場出来ました. (確か7が偶然解けてボーダー丁度ぐらいの点数で本選に行った) しかし本選では実力不足で結果を出せませんでした.

中三のときはJJMO予選は余裕だろうと思って何も対策しなかったら相性の悪い問題(マス目系な問題)を大量に引いて(しかも整数が簡単だった)まさかの予選落ちをしました. 後でJMO解いたら通りそうな得点が取れたのでかなり悔しかった.

中学にいたときは本を中心に勉強していた記憶です. これが失敗でした. 主に解いた本はパーフェクトマスターシリーズとJMO, JJMOの過去問です. 正直これらの問題集は載っている知識等の量がかなり貧弱です.(例えば根軸とか反転とかは載ってないし典型考察も強調されていない) さらに各問題が解答にある方法で何故解けるのかについての言及もほぼ無かったので(普通無いが)そのようなものを考えるべきだという発想に至りませんでした. 単に問題を沢山解けばよいと思っていました.(受験数学や数検一級はそれでなんとかなっていたので) これが中学にいたときに実績を残せなかった最大の要因だと今になって思います.
他には高校数学の美しい物語とかも読んでましたね. 情報量が多くて面白かったですが記事であるという特性上単発の知識感があって身につかないところも多かった記憶. (サイトがシンプルに数オリの傾向の変化に対応しきれて無いという可能性もあるけど)

高一(JMO2021)-予選敗退

中三の終わりから高一ぐらいになってようやく解けなかった問題を中心に何故解けなかったのかを考える癖がつきました. (当時はメモ帳に色々メモをしていたがTwitterを始めてからはそこにツイートしているのでよかったら見てみてね)

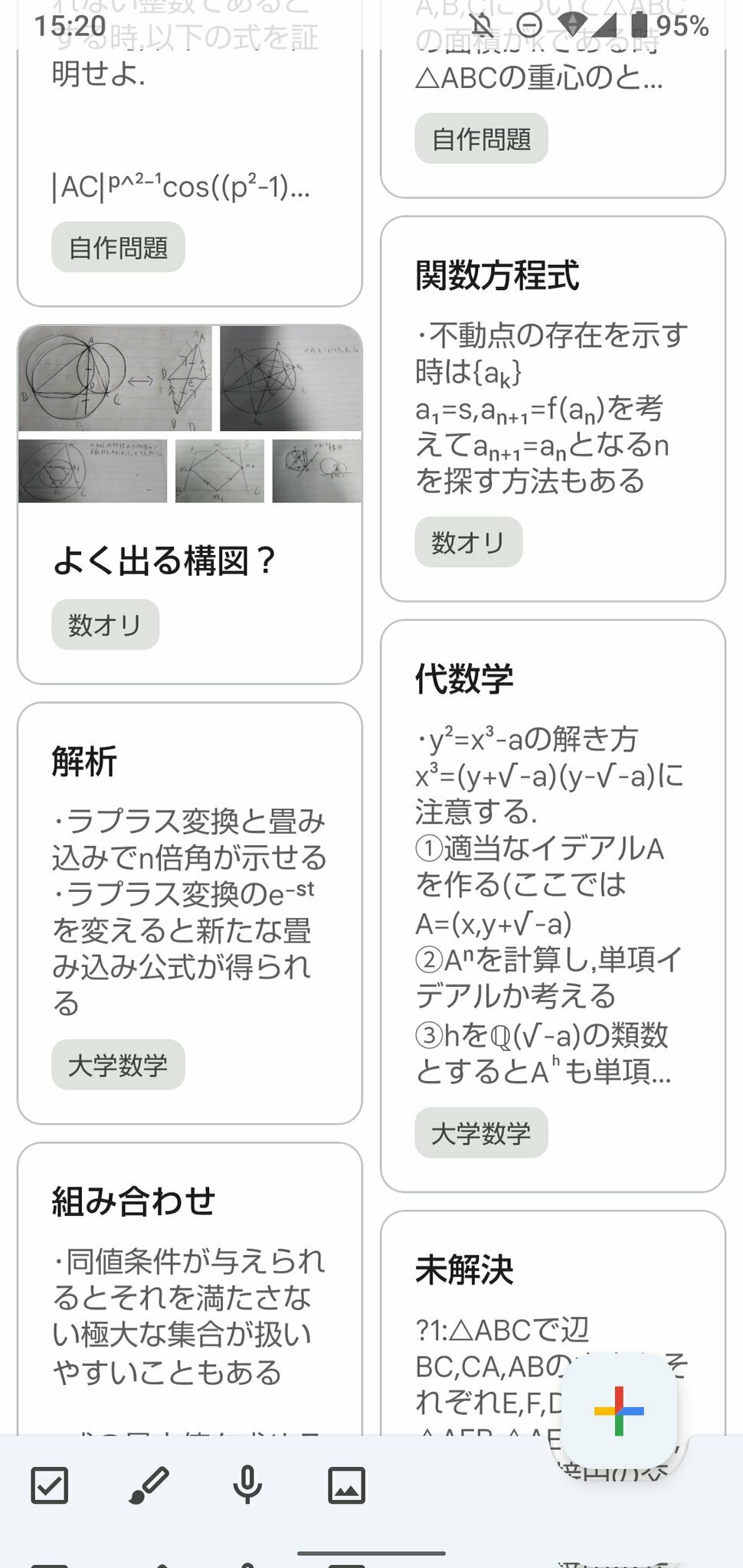当時のメモ

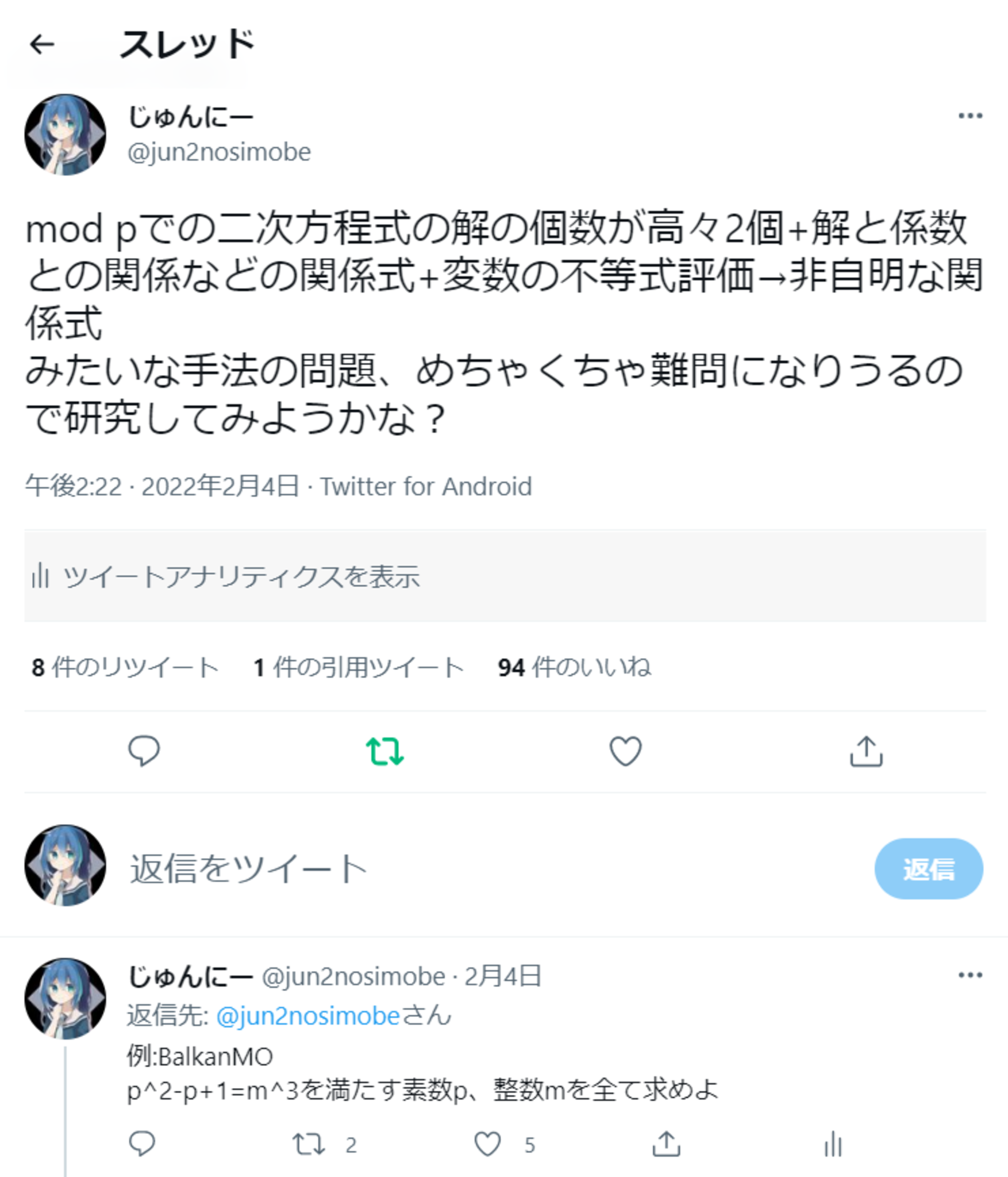かなり最近のメモ

これの背景には獲得金メダルや三角形と円の幾何学とかで新たな視点を手に入れた事がありそう(後者の本は数オリ対策というよりかはお話として面白かった). あとは大学数学で自分が面白いと感じる事が増えてそれを言語化する癖があったのも大きそう.
当時は解けない問題があったら類題を作問してやろうぐらいの勢いで問題と向き合ってましたね(流石にやり過ぎ？)

例えばこれはまさに一例ですね. (フェルマーの小定理等による位数の議論, 不等式評価)

これのお陰かこの手の問題は自分の得意分野です.

この頃から競技プログラミングにも手を出し始めた記憶です. グラフの問題とかDPの知識などは数オリに少なからず役立ったかもしれないと思いますが純粋に競プロ自体が楽しかったです.(大学入ったら再開したい)

この年に解いた数オリの問題はJMO予選の過去問を15年分ぐらい(とりあえず予選対策をしたかった)とOMCの問題, あとは適当な数オリ対策本の問題とかですかね… 大学数学とか鉄緑の勉強, 競プロやらで意外と精進出来ていない？！
IMOshortlistとかはあまり解いてなかった記憶(本選以降はまだ早いという感覚があった気が)

そしてJMO予選を受けました. 過去問では余裕で予選通過だったので行けると思ったら問2,3から苦手な感じの幾何, 問4がめんどくさい問題という感じで大失敗をしました. その上で本選出場者人数が絞られてしまい. 予選落ちという羽目になりました. かなりショックでした.(このショックから2月に有志コンを作りましたね, 懐かしい) これ以降自分が競技に参加するとき上位を狙う事は辞めて競技自体を楽しむという方向にシフトしていきました.
また, もう予選とかどうかを気にせずどんどんIMOshortlistの問題とかも解くようになりました.

そして高二,高三

高二になると鉄緑が非常に忙しくなりました. 後半に数オリや情オリがある事から前半はかなり受験勉強を中心に勉強していました. (これのお陰でIMOまで6ヶ月ノー勉でもなんとかなった(?)) このときはIMOshortlistを中心に勉強しました. 面白そうな問題を探してのんびり考察するみたいなノリです.
JMO予選直前はかなり病みました. これで予選落ちだったら本当に救いようがないので. 本当に何にも手がつかなかったぐらい病みました. 結局これは杞憂に終わり本選に進めました. 本選対策はJMO本選の過去問を中心にしました.(別にこのタイミングまで過去問を残す必要があったのかと聞かれると微妙です. 記述式の他の数オリの問題で十分対策出来ますし) JMO本選は一発ゲーは少なめでやりやすい問題が多いなという印象だった記憶です. (4,5番も手数が多く部分点が期待出来るかもなという気分になった)

本選も問題を楽しもうという気持ちで臨みました. 本選の受験会場が3年前のJJMO本選の受験会場と同じだったのは少し感動でした.(中三は中央大学が受験会場で高1はオンラインだったので本当に久ぶりの早稲田大学だった, あの頃より自分は変わったのかなとか思い感慨に浸りました) そして試験開始. 一問目のCと四問目のNに目が行きました. 例年は得意のNが一問目にあり差がつきにくい事が多かったのですが今年は4問目と最も差がつきやすいところに配置されており始まった瞬間ガッツポーズをしました. 1問目は本質はすぐ見えましたが記述が面倒だったので時間配分を考え雑な記述で2番に移りました.(実際1番は半分の議論しか回って無くて5/8しか取れてなかった) 2番は関数方程式.(去年の春合宿の問12(家で解いたら解けた)と似ていた) まあ解けるだろうという気分. 単射あたりがすぐ言えて, そこからネストの構造を活かした代入をすると一気に情報が手に入り後は何やっても解けるみたいな記憶. 3番は幾何でした. 作図に手間取ったので先に4番の不定方程式に手を出しました. まずは $x,y$ 小さい値を代入し, 次に$\bmod4,3$あたりを試しました. すると何か$\mod4$から$\mod8$,$\mod16$,...のような議論が出来るように感じました. なので一般化して$\mod 2^n$として($n$は$x,y$あたりが$2$で割り切れる回数とかだった気がする)議論をするとLTEが回ってくれて議論が進みました. さらにここから得られる情報から左辺が因数分解でき, それによって不等式評価出来そうという気分になった.(因数分解→不等式評価はISLか何かで見て(大学数学とかでも重要なので)覚えていた記憶) これが$10$分から$15$分ぐらいで出来た(?!). 記述は大変だったので結局答案書き終えるのには$1$時間程度掛かった記憶. 三番は図を描いたら結構理詰めで解けた記憶(詳細は覚えていないが少し回りくどい事をしてしまった記憶). 五番を考察する時間は$30$分しか無かったので条件をグラフっぽく言い換えるだけで終了した. もう少し解の評価に関する考察をすれば得点になったかも知れない. あとは一番の答案を改善する方がよかったかもだがこれは結果論なのでどうしようもないし問題を楽しむ事を目標にしていたので後悔はない.

裏面に続くを書き忘れて終わった後試験監督に頼んで書いたりするというハプニングがあったが銀賞を獲得し, 春合宿に進めた. まずAPMO対策として過去問を解いたが結構自分好みだった記憶. APMOは問題を沢山解こうとして見直しをしなかったらミスを大量にしてしまい, 少し残念.

春合宿

さて春合宿である. APMOから春合宿まではIMOshortlistを中心に勉強した気がする. 春合宿初日, 表彰式に思わぬハプニングが起こった. 風邪を引いたのである. 念のため病院に行ったらPCR検査を受ける羽目になった. もし陽性だったら春合宿に参加出来なかったが陰性だったので一安心.

試験初日

1 C2
2$ f:\mathbb R\rightarrow\mathbb R$ $ f(xf(y)+f(f(y)))+yf(f(x))=f(f(y)f(f(x))+f(y))+xy$(らしい, 忘れた)
3 N7
まず全完を目標にした.
1番は解の評価は比較的すぐ出来たが証明の方で迷走してしまったので2に逃げた. 2は去年の春でも似たような問題が出ており, それが理詰めで解けたので解けるだろうという気分になった. 実際自明考察をした後, 不動点に関する議論をしたら普通に(手数は多いものの)解けた. その後1番に戻ってくると普通に評価が回りそうな議論を思いつき, そのまま鳩ノ巣原理に気付いて解けた. 3番を残すのみ. 2時間以上残ってた記憶(?)しかし自分が試験時間を一時間間違えており, あと一時間で試験が終わると勘違いし, 急いで議論を進めた. すると序盤で致命的な嘘を埋め込み, その後ももう一つ嘘を埋め込み死亡した. 嘘をついていた事に試験後気付いたときは発狂した. (自分が話した)参加者には2完が多かった.

二日目

4 A3
5 N4
6 MNを直径とする円ωの内部にAがある。N中心、半径NAの円とωの交点がB,C。BC上に∠BAP=∠CAQなるPQを取る。NP,NQとωの交点がそれぞれX,Y。XQ,YP,AMが一点で交わることを示せ。(らしい)
とりあえず2完を目標にした. 4番は答えの予想を間違えて沼ってしまった. 帰納法の議論がうまく行かず5に逃げた. 5は問題文を数学の言葉に直す事が本質で後は(分母)$-$(分子)あたりの$\bmod$をとると上手く行った気がする.(焦って適当に議論したら強化合宿で貰えた答案の添削でボロクソに言われてた) 再び4の考察を始めた. 帰納法について考えていたら答えが$2^n$毎に変わる事にようやく気が付き, これを帰納法で示す事にした. 答えの予想を間違えた時の帰納法のフォーマットを使ったのでかなり証明に苦戦した. 6を考察する時間は$30$～$45$分程度だった記憶. 自明考察だけ書いて終了.
この回も2完が多く波乱が少なかった. 明日辺りに何か起こりそうという気分になった.

三日目

7 G1
8 意味不明すぎ, 省略
9$f:\mathbb R\rightarrow \mathbb R\ \ f(x)f(y)-f(x+y)=yf(x)-f(x+f(y)), \ \ f(-1)=-1$(らしい)
2完を目標にした. 8が解けなくても9がFEなので希望があるなという気分に. とりあえず7を考察した. が, 何故か解けない. 根心の議論はすぐに思いついたがそこからのangle-chaseが何故か回らず一致法とかいろいろ迷走した. 1,2時間粘って分からなかったので気分転換に8を考察. が問題文が意味不明に長く, しかもめちゃくちゃ複雑. 無理. 9にも目を通す. これも単射系の議論が上手く回らず. とりあえず7を解かねば... が, 解けない. 解けない. 解けない. 解けた(試験開始4時間後). 何か適当な場所の交点取ったら共円があってangle-chase出来た. なんで沼ったのかはよく分からない. しかも何か議論に不備があって1点減点されてた. 試験終了後みんな8,9が解けてなかった事を知ったときは本当に安心した. (7を解いている間30分～1時間おきにため息をついていたらしいが隣の北村氏はこのため息のたびに私が問題を解けていると勘違いして焦ったらしい()) もし7が別の日に出ていたら詰んでいたかも知れない. チューターの人に7に苦戦した事をめっちゃフォローされたのが面白かった(逆に最終日の幾何へのプレッシャーが増えた())
ここまであまり差がつかなかったので最終日が勝負の分かれ目になりそうという感じだった.

最終日

10 N3
11 G4
12 C6
とりあえずしっかり2完する事を目標にした. 10はNなので絶対解けると思い考察を始めた. 最初約数列の前半の方の決定を最小の素因数を取る等して決定し, この議論を繰り返せば終わると思って粘った. しかしこれだけでは不十分で$4$項目あたりまで決定した後帰納的に約数列が決まることに気が付き解けた.(1時間ぐらいかかったのは想定外) 11は解かないと目も当てられないなと思いながら解いてた(). しかし結構早い段階でaminoの補題に気が付きaminoありがとうという気分になった. その後は相似とかを使って気合いの長さ計算が回ってくれて解けた. 12を残すのみ. 正直これが解けるとは思っていなかった. 最初はみんなと同じでウサギが勝つと思っていたが, $1$次元でハンターが勝つ事とその方法が$2$次元に応用出来る事に偶然気が付き解けた. 自分の構成で上手く行く事の証明は適当だったが1次元のアナロジーである事を明示していたので助かったのかなとか思っている.

結局$8$完で$770770600777$の計$55$点, 分野別には$A14, G13, C14, N14$点とめちゃくちゃバランスの取れた得点で代表に選ばれた. (正直代表になる気はそこまで無かったので驚きだった)

試験以外に関して

普段ではTwitterを通じてぐらいしか数学の話が出来なかったが春合宿ではみんなと一緒に問題を解いたり問題について話したり出来て楽しかった. こういう会の存在を中学とかの間に知れなかったのが残念で仕方が無い. 中高生は春合宿がめちゃくちゃ楽しい事をもっと知って欲しい.

そしてIMO

代表に選ばれてからは(特に強化合宿後は)めちゃくちゃ数オリの勉強をした. IMOshortlistだけでなく, 各国のTSTやUSAMO, あとは通信添削をやった. 直前は幾何を重点的に勉強した. 受験勉強との両立は途中で諦めて数オリに全振りした.
IMOは久々の現地開催だからかめちゃくちゃ盛り上がっていた. 英語をこんな形で使うとは思いもしなかった. 国際交流や他の代表と遊んだりするのが楽しかった. なんか中学生の時とかは天才の集まりみたいに思っていたがどちらかというと何かお祭り騒ぎだなみたいなのが率直な感想です.
試験問題
初日は全完を視野に入れていた. 1は問題文の把握に苦戦し見事に誤読した.(幸い問題の本質部分は変わらなかったので6点取れた).2はまあやれば出来たが自分は数オリでよくある議論(?)一意の$y$を$i(x)$と置く事, 並べ替え不等式的議論)が出来て楽しかった.(無論, 時間をかければもっと初等的に解けるだろうが)3の初動は上のツイートの考察が的中して見た瞬間に$2$点の部分点に当たる考察が出来た. しかしここから先の議論は眠さと2完した安心から上手く進まず$2$点止まりだった. 悔しい.
二日目はGが4番にしかなく残念だったが, 5が整数だったのでガッツポーズした. 4は作図に苦戦したが少し考えるとaminoの補題が見えて解けた. 変な補助点を使って相似を示したので場合分けが発生して面倒だった. とにかく amino, thanks again! 5は約数系の議論と不等式評価で解ける問題だった. 階乗の情報量が多すぎて何をやっても解ける問題になっていたのが少し残念. 自分は$\bmod p-1$とかいうアクロバティックな事をしたよ. (これの背景はprime-constraintのpdfを見てね) 6は構成ゲーである事に気付かずさらに嘘評価を入れてしまった事で根本的に方針を誤ってしまった. 残念.
結局$672771$の$30$点で銀メダルだった. (自分は参加できたこと自体が楽しかったのでメダルの色はそこまで気にしてないけど)

これから競技数学と如何に向き合うのか

自分はIMOに参加出来たもののかなり迷走が多かった方だと思っている.(特に中学の時は迷走しかなかった) それと同時に, 数オリ(もっと言えば数学)に限らず色々な分野について触れてきた方だと思う. なので自分はまず後輩達が数オリの勉強で迷走する事を減らすべく, 自分が知っている情報を共有したり, 自分が得意他と思っている整数論について自分の知見をまとめようと思っている.(丁度LTEやprime-constraintの記事とかの改訂, 続編の公開に当たる) さらに競技数学だけでなく大学数学も色々勉強してきたので競技数学と大学数学の懸け橋的なpdfを書いてみたり, 知見の共有等が出来たらよいな思っている.(最近競技数学徒は増えていて嬉しいが大学の整数論に興味を持ってる人とかが余りいないので寂しく思っている)
とりあえず疲れてきたので記事はこれぐらいで終わりにします. ここまで読んでくださりありがとうございます！