解説高校数学

相似比2:1の正多角形内接の定理

三角関数,初等幾何,正多角形

626

はじめに

　この記事では、先月私が偶然発見した正多角形に関する超面白い性質を紹介したいと思います。
　ちょっと長いので、お急ぎの方は証明の部分は飛ばして、超面白い性質の部分だけでもご覧いただければと思います。

正 $7$ 角形の場合

　まずは、最初に正 $7$ 角形の場合について。
　下の図をご覧ください。

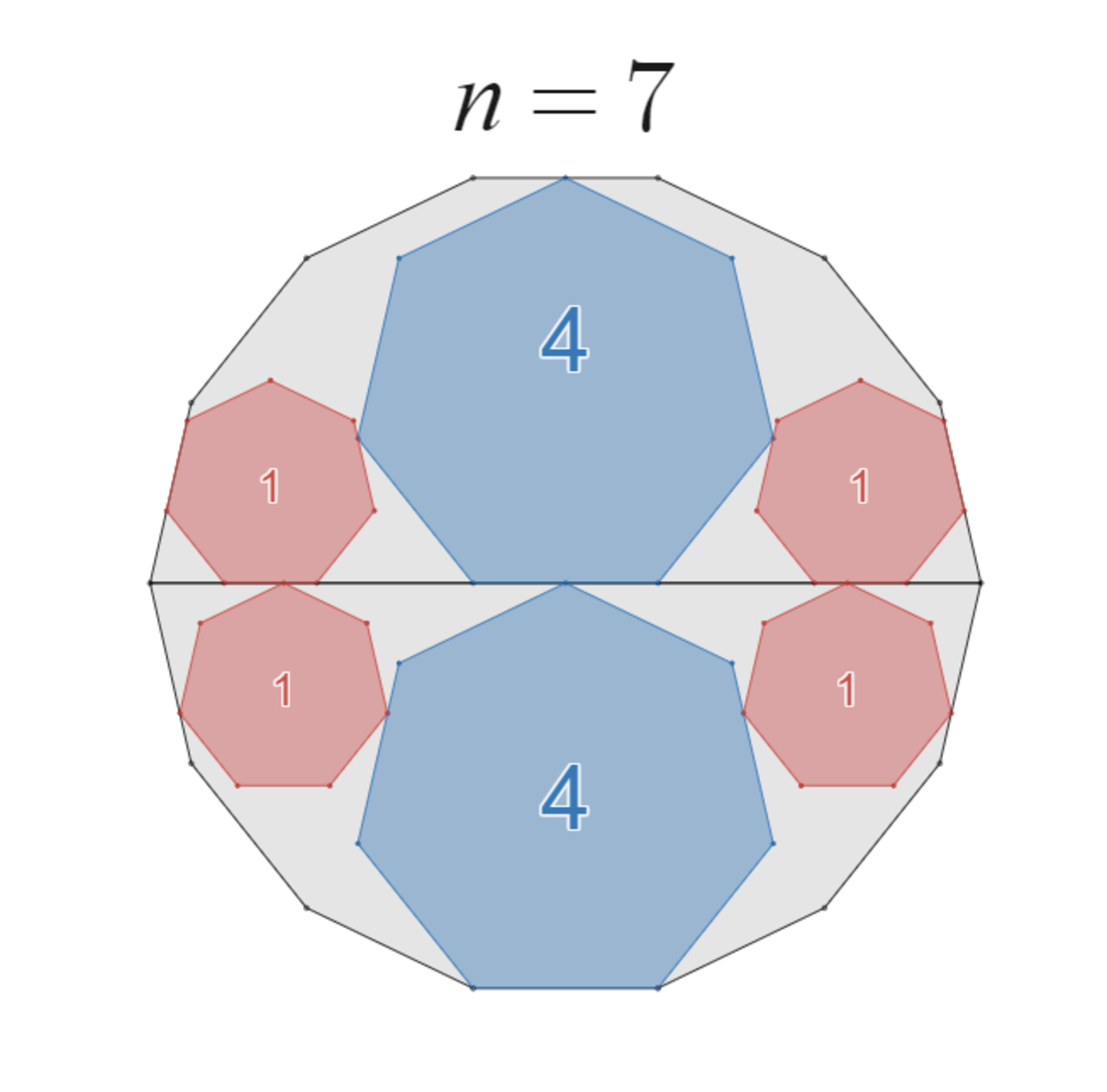正７角形の場合

見つけた性質は次のようなものです。

一辺の長さ $1$ の正 $7$ 角形(赤色) $4$ つと、一辺の長さ $2$ の正 $7$ 角形 $2$ つ(青色)は、一辺の長さ $2$ の正 $14$ 角形(灰色)とその最長の対角線に、図のようにピッタリ接するように配置することができる。

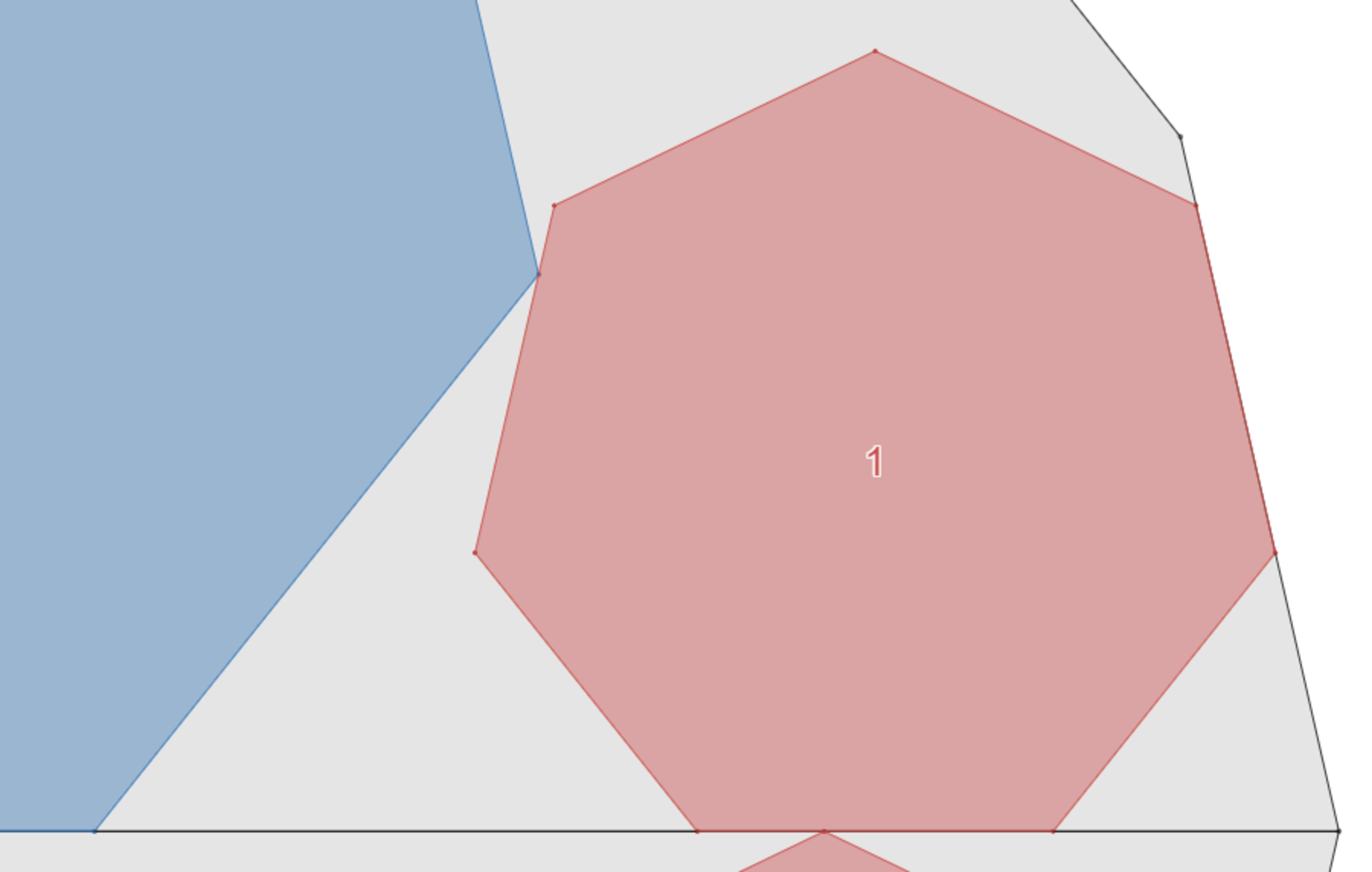拡大してもピッタリ接している

図中の $4$ とか $1$ の数字は面積比を表しています。
また、各正$7$角形の向きは全部同じです。

　この性質を見つけたときは本当にビックリしました。作図ソフトgeogebraで作図したら接しているように見えたので、座標計算で確かめてみたら確かに接していたのです!

　(正確に言うと、私が最初に発見したのは「上半分」の部分だけで、その後で下半分の部分でも成立することを教えていただいたのですが。)

一般化

　次に、正 $9$ 角形の場合にどうなるかやってみると

正 $9$ 角形の場合

　これまたピッタリ接しました!

　正$7$角形の場合と正$9$角形の場合についてよく見ると、接し方には$2$つのパターンがありそうです。

　赤い小正多角形の「辺」が他の正多角形と接している場合と、赤い小正多角形の「頂点」が他の正多角形と接している場合の$2$パターンです。

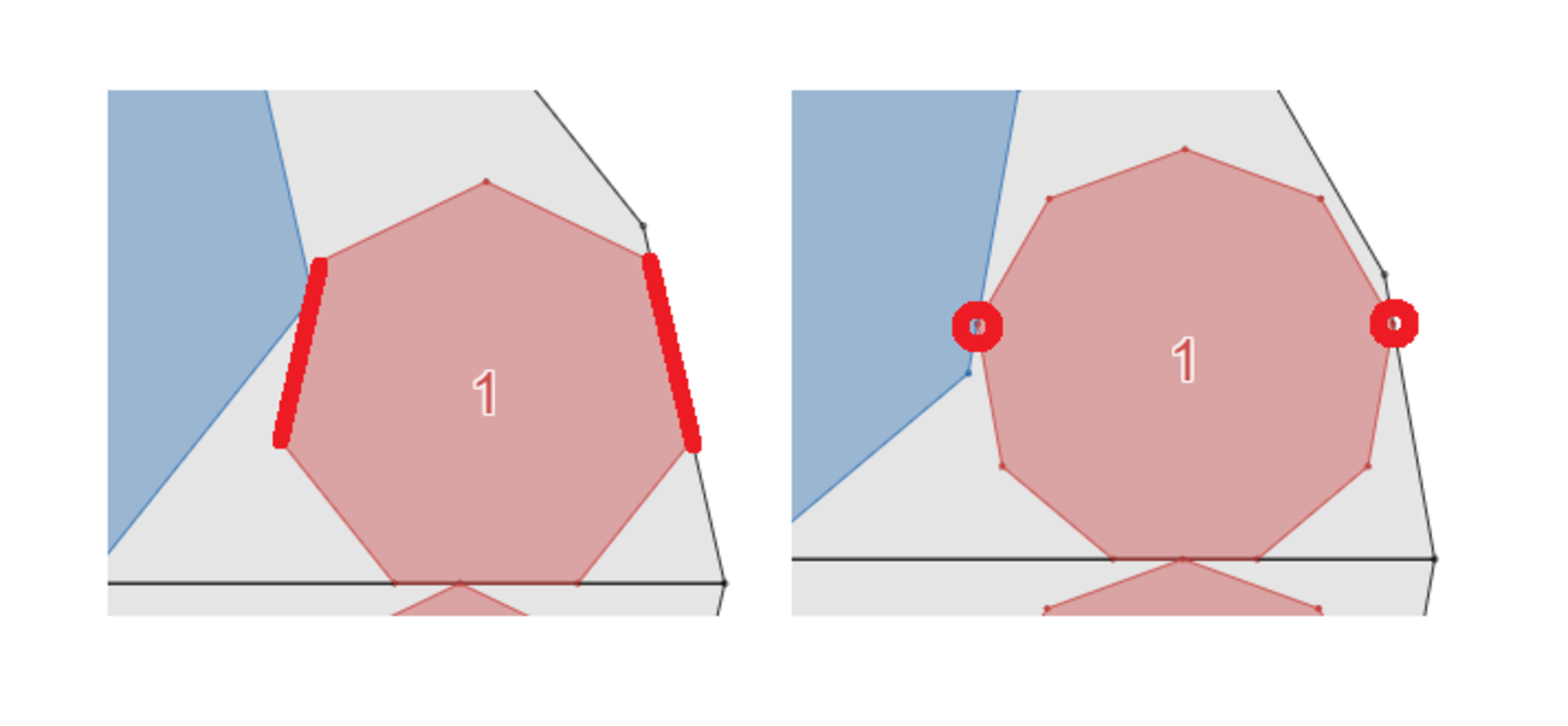小正多角形の「辺」で接触する場合と「頂点」で接触する場合がある

　この事実そのものも面白いですが、後で証明の場合分けのときに使いますので、頭の片隅にとどめておいていただければと思います。

　さらに他の正多角形で試してみると・・・

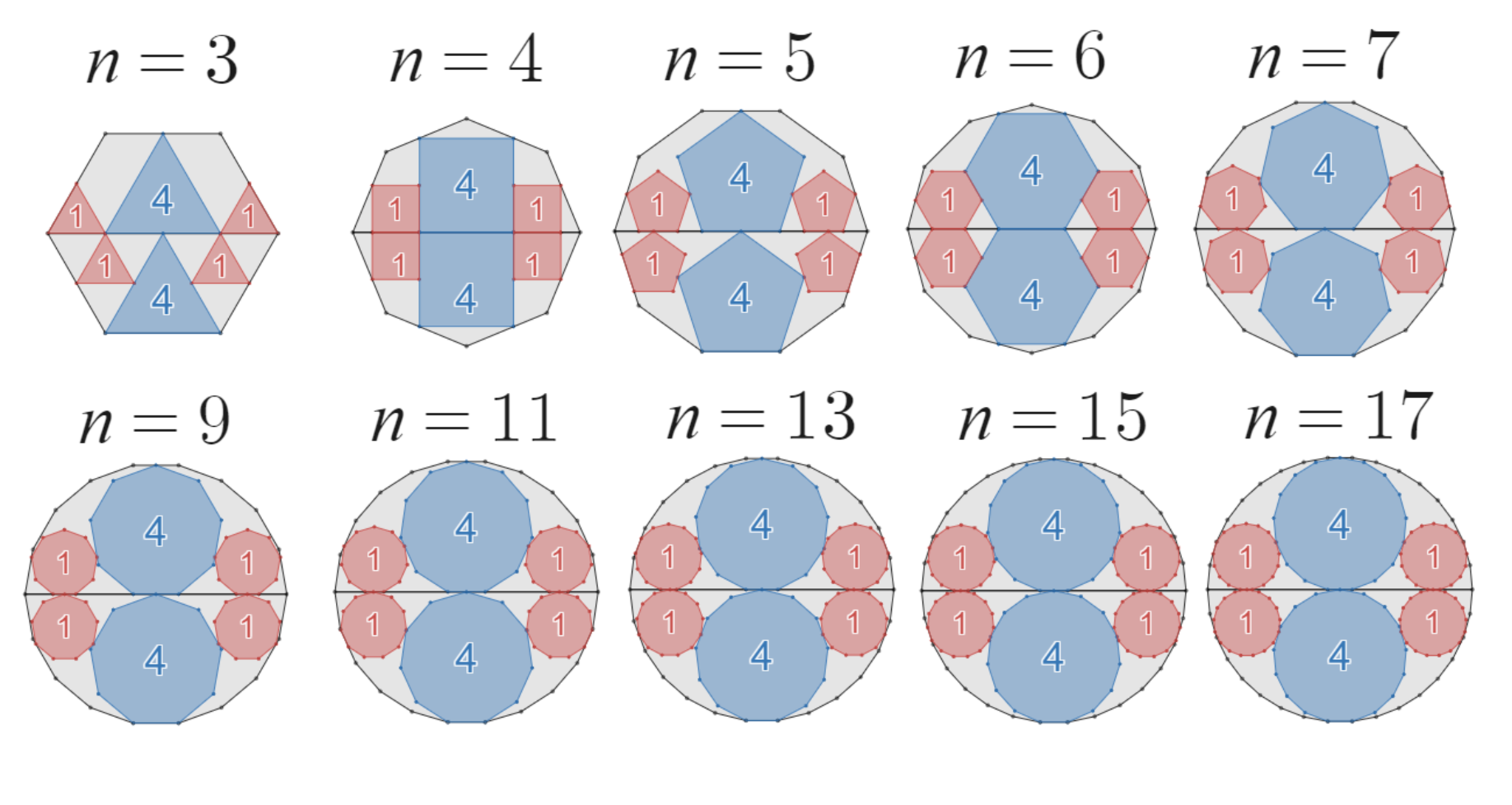同じ性質が成り立つ多角形たち

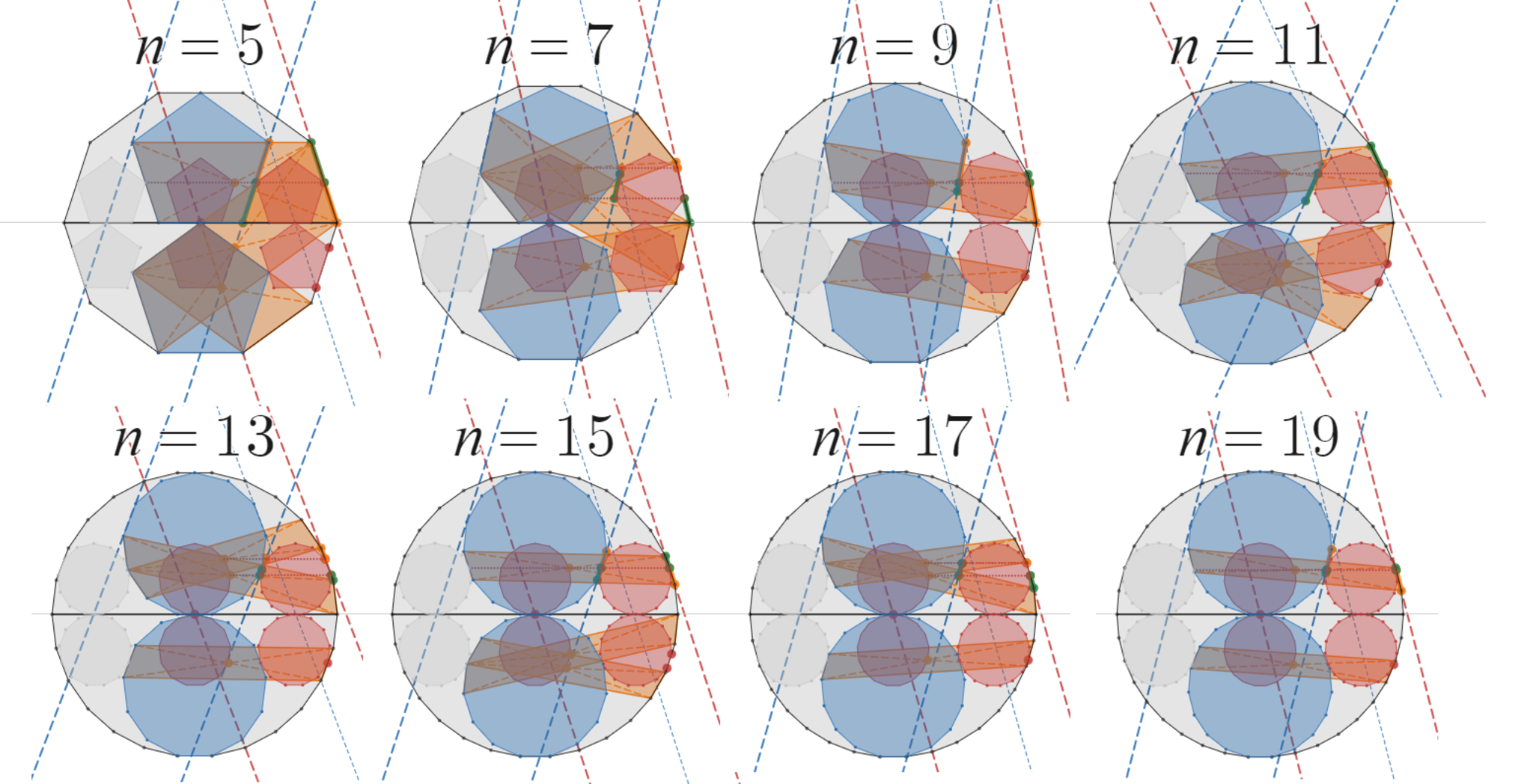
　なんと、多くの正多角形で同様の性質が成り立つことを発見しました!
　ただし、上の図を見ていただくと、$n=8,10,12,14,16$ の場合が飛んでいます。
　実は、$n=8,10,12,14,16$ のときはこのような配置にしてもスキマができたりはみ出たりしてピッタリ接するようにできないのです。

!FORMULA[21][38042][0] が8以上の偶数のときはズレてしまう

$n$ が8以上の偶数のときはズレてしまう

　このように、残念ながら $n$ が偶数のときはほとんどの場合成り立たないのです。
　しかし、$n$ が$17$以下の奇数のときは必ず成り立っています。

　もしも、$19$ 以上の奇数についてもこの性質が必ず成り立つ、言い換えると「$n$ が$3$ 以上の奇数であれば、すべての$n$についてこの性質が成り立つ」としたら、すごいことだと思いませんか?

　実は、この性質は** $n$ が $3$ 以上の奇数のときは必ず成り立つ**のです!!そのことを証明することに成功しました!!すごい!!(自画自賛)

偶数の場合

　繰り返しになりますが、$n$ が偶数のときは先の性質はほとんどの場合成り立ちません。しかしながら、ほんのちょっと修正すると、偶数の場合にも必ず成り立つようにすることが可能です。
　次の図を見てください。

正 $10$ 角形の場合

　図中の $16$ とか $4$ とか $1$ の数字は面積比を表しています。
　次のような性質が成り立っています。

一辺の長さ $1$ の正 $10$ 角形(赤色) $4$ つと、一辺の長さ $2$ の正 $10$ 角形 $2$ つ(青色)は、一辺の長さ $4$ の正 $10$ 角形(緑色)とその最長の対角線に、図のようにピッタリ接するように配置することができる。

　$n$ が奇数のときは内側が正$n$角形、外側が正$2n$正角形で、辺の数が倍になっていましたが、$n$ が偶数のときは内側が正 $n$ 角形、外側も正 $n$ 角形で辺の数は同じです。そのかわり、外側の正 $n$ 角形の一辺の長さは奇数の場合の倍の長さになっています。

他の正偶数角形についても、同じ配置にすると確かに接していることがわかります。

正偶数角形を接するように配置

証明すべき命題

ではここまでの内容を一旦まとめたいと思います。

相似比2:1の正"奇数"角形内接の定理

$n$ を $3$ 以上の奇数又は $4$ 又は $6$ とする。

$xy$ 座標平面上の原点を中心とし、辺の一つが $x$ 軸と平行になるように一辺の長さ $2$ の正 $2n$ 角形 $A$ を配置する。

$y$ 軸上に中心をもち、中心より下にある辺の一つが $x$ 軸と平行、かつ一辺の長さ $2$ の正 $n$ 角形 $2$ つを、$A$ に内接しかつ $x$ 軸と接するように配置する。それらのうち中心の $y$ 座標が正のものを $B_1$、負のものを$B_2$とする。

このとき、$B_1$又は$B_2$と外接し、かつ　$x$ 軸とも接するように、「中心より下にある辺の一つが $x$ 軸と平行、かつ一辺の長さ $1$ の正 $n$ 角形 $C$ 」を配置すると、$C$ は必ず $A$ に内接する。

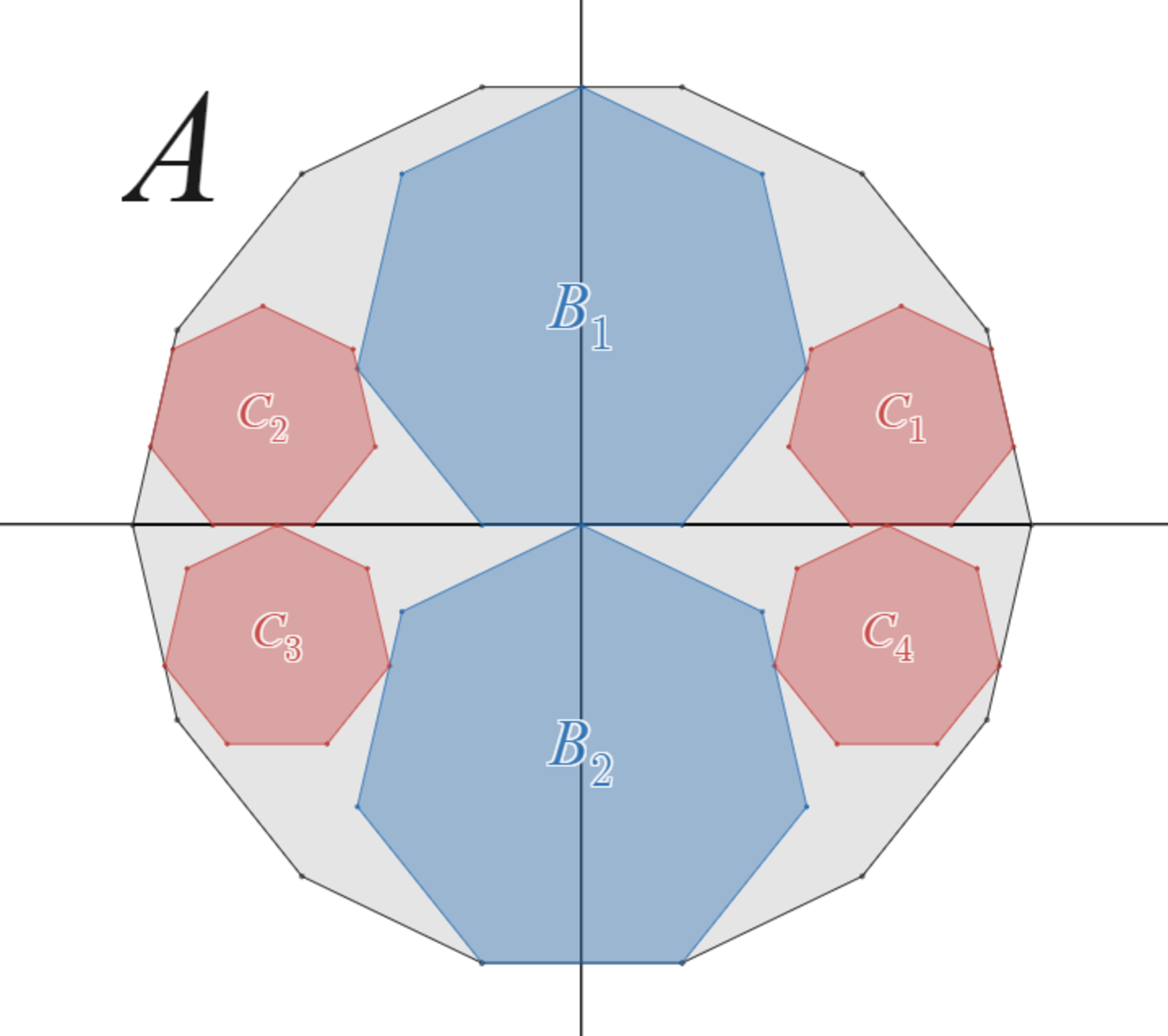相似比2:1の正"奇数"角形内接の定理

相似比2:1の正"偶数"角形内接の定理

$n$ を $2$ 以上の偶数とする。

$xy$ 座標平面上の原点を中心とし、辺の一つが $x$ 軸と平行になるように一辺の長さ $4$ の正 $n$ 角形 $A$ を配置する。

$y$ 軸上に中心をもち、辺の一つが $x$ 軸と平行、かつ一辺の長さ $2$ の正 $n$ 角形 $2$ つを、$A$ に内接しかつ $x$ 軸と接するように配置する。それらのうち中心の $y$ 座標が正のものを $B_1$、負のものを$B_2$とする。

このとき、$B_1$又は$B_2$と外接し、かつ　$x$ 軸とも接するように、「辺の一つが $x$ 軸と平行、かつ一辺の長さ $1$ の正 $n$ 角形 $C$ 」を配置すると、$C$ は必ず $A$ に内接する。

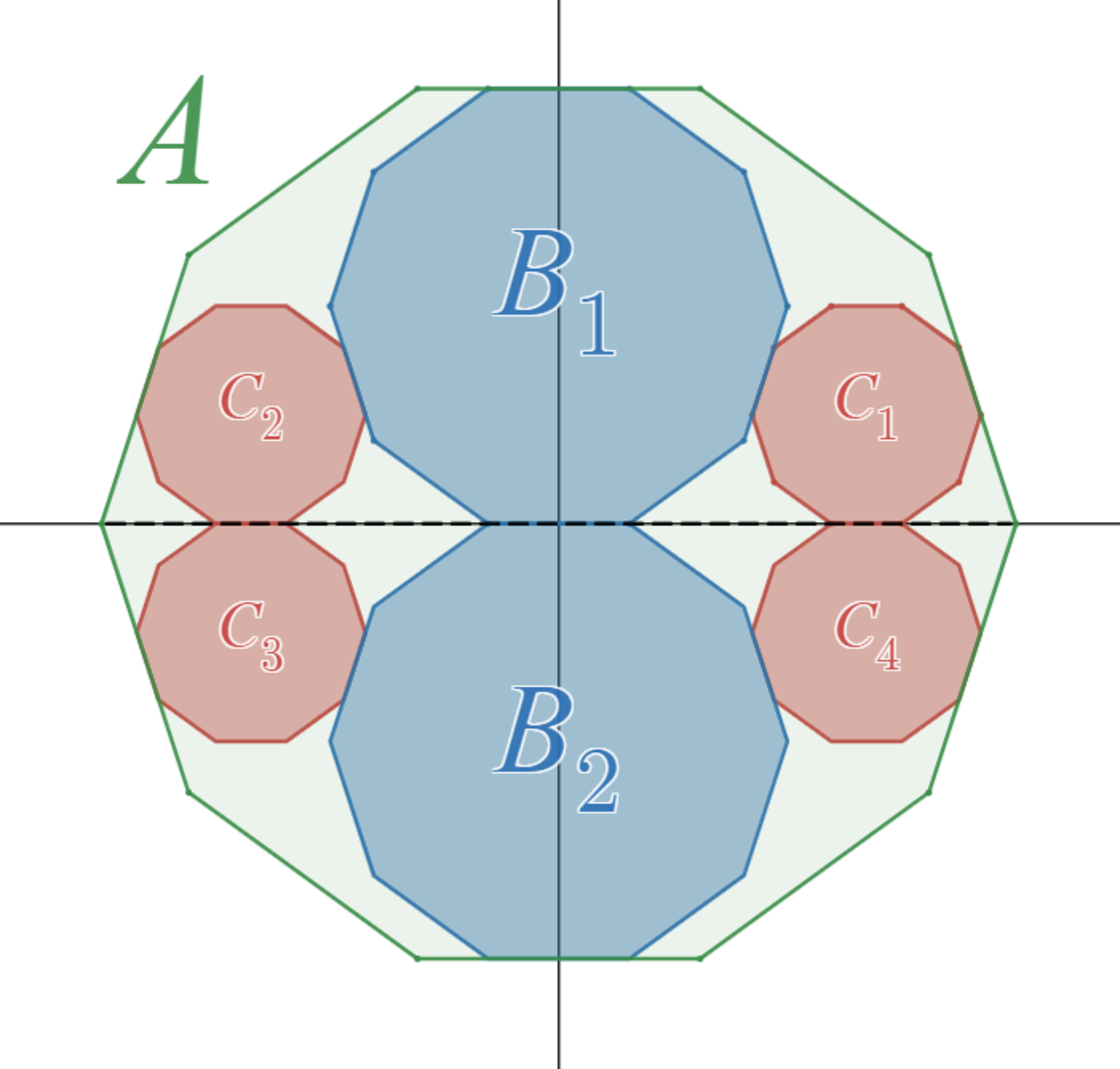相似比2:1の正"偶数"角形内接の定理

$C$ の場所は $4$ 箇所ずつあります。便宜上、象限にあわせて $C_1$ ～ $C_4$ と添え字をつけています。
「定理」の名前は適当に付けました。もし「こんな名前の方がいい」とかあればコメントいただければと思います。
ではいよいよ証明パートに入りたいと思います。

正"奇数"角形の場合の証明

まずは、正"奇数"角形の方から証明します。
$n=3,4,6$ の場合については、座標計算で容易に成立が確認できますので、ここでは $n$ が $5$ 以上の奇数の場合だけ考えることにします。

上半分の証明

　正"奇数"角形の場合、上半分と下半分で配置が異なるため、まず上半分から証明します。
　証明のために、各頂点に名前をつけることにします。

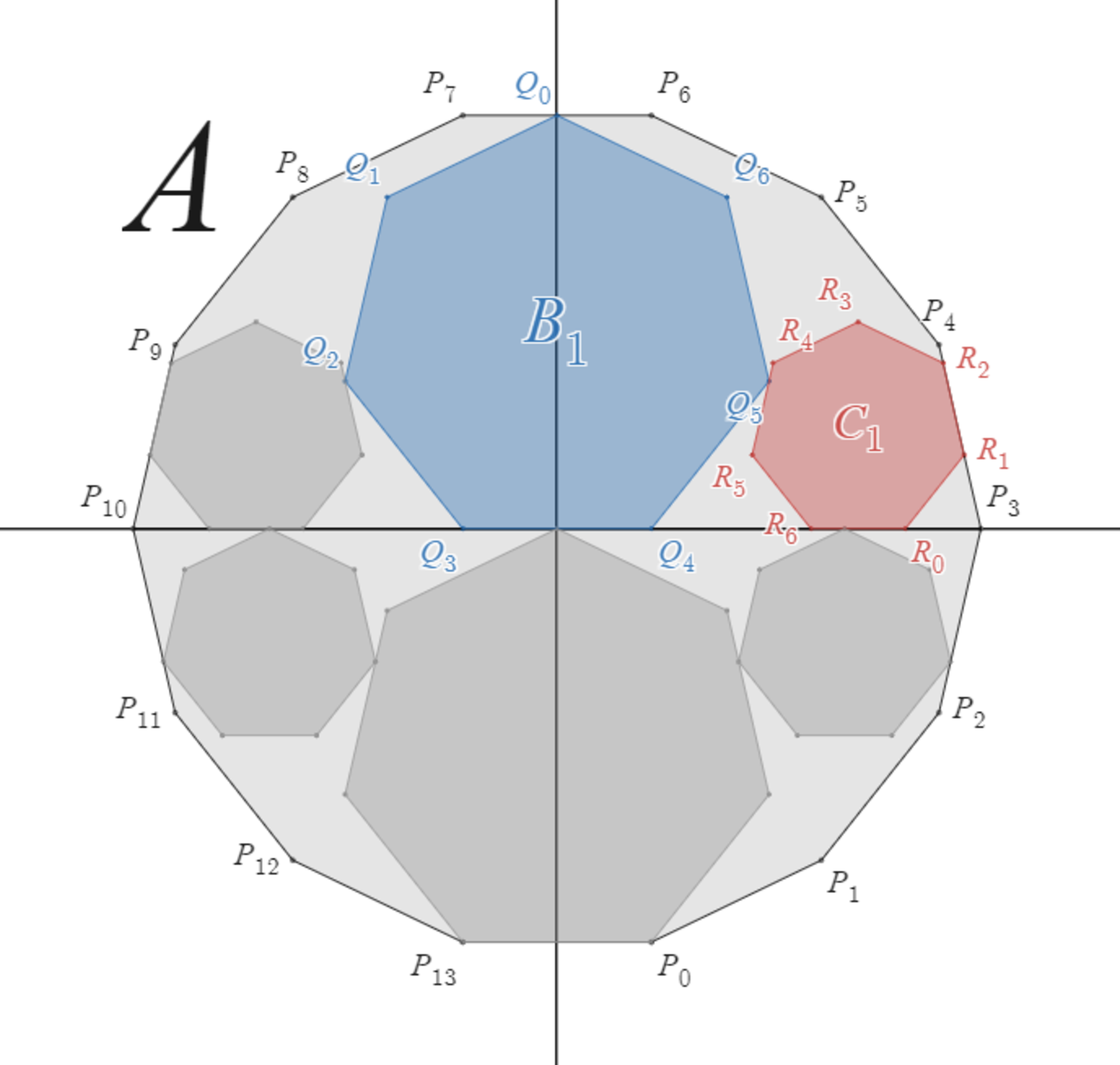各頂点に名前を付ける

図のように、$A$ の頂点のうち $y$ 座標が一番小さく $x$ 座標が正の頂点を $P_0$ とし、そこから反時計回りに順に $P_1,P_2,\cdots$ とします。

$B_1$ の頂点のうち $y$ 座標が一番大きい頂点を $Q_0$ とし、そこから反時計回りに順に $Q_1,Q_2,\cdots$ とします。

$C_1$ の頂点のうち $y$ 座標が $0$ で $x$ 座標が大きい方の頂点を $R_0$ とし、そこから反時計回りに順に $R_1,R_2,\cdots$ とします。

　最初に次の補題を考えます。

補題

$Q_k,Q_{k+1},P_{2k},P_{2k+1}$ を頂点とする平行四辺形の対角線の交点を順につなぐと、一辺の長さが $1$ の正 $n$ 角形を描く。
特に、その交点は $R_k$ と $y$ 座標が一致する。

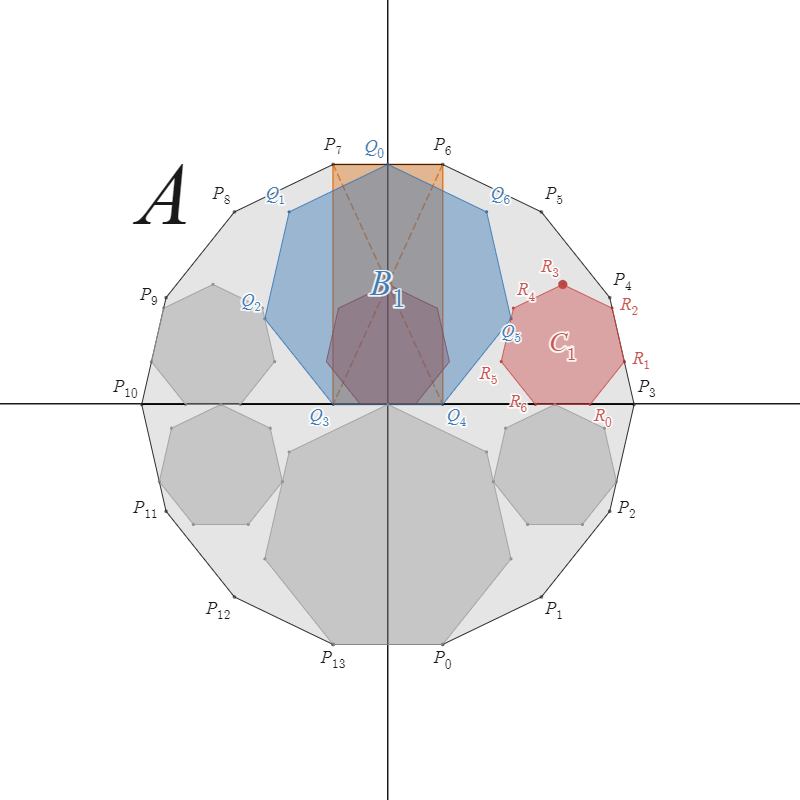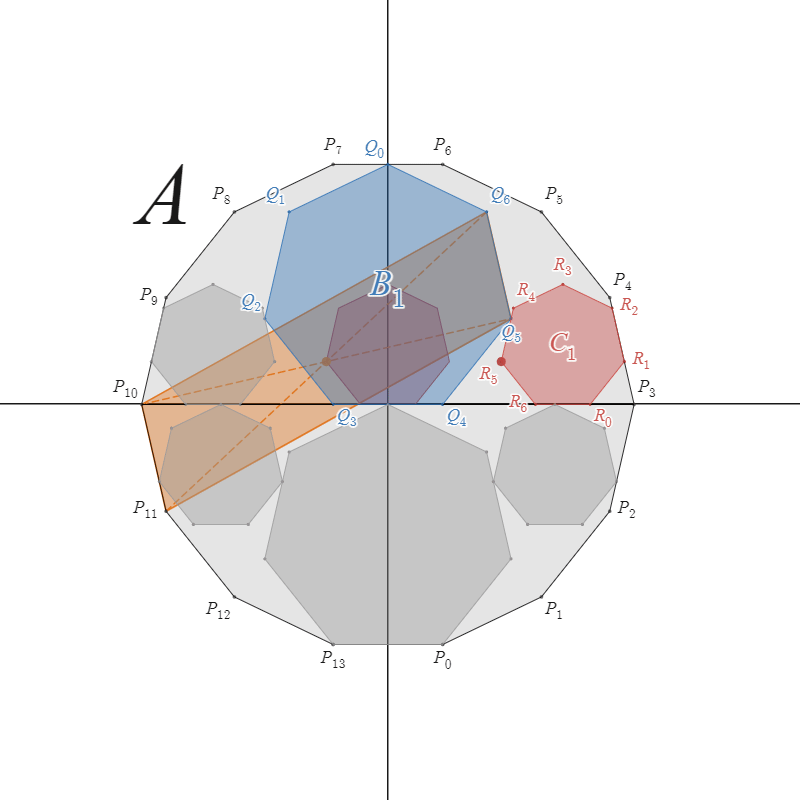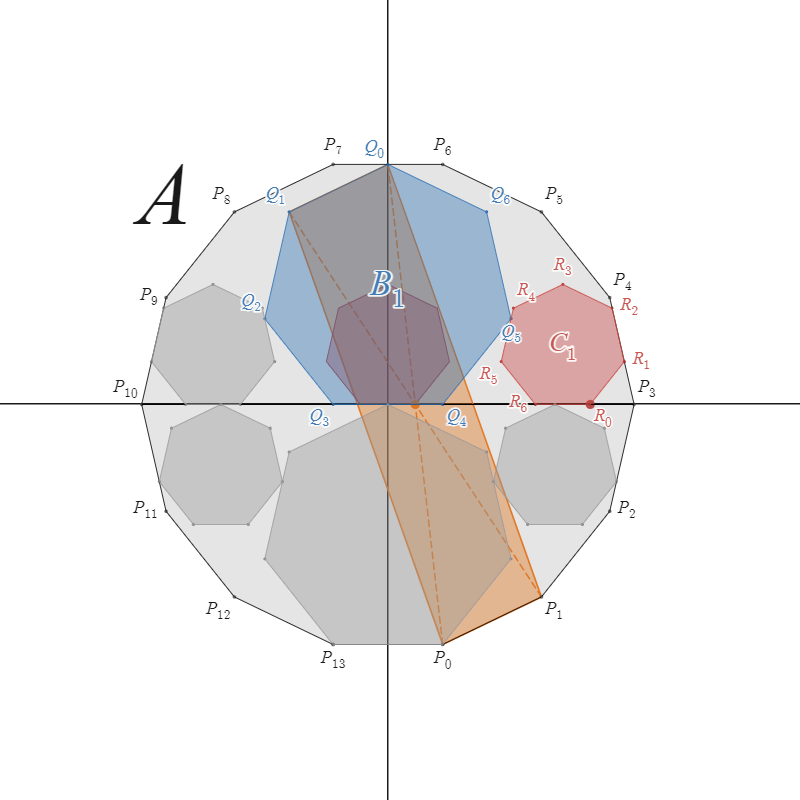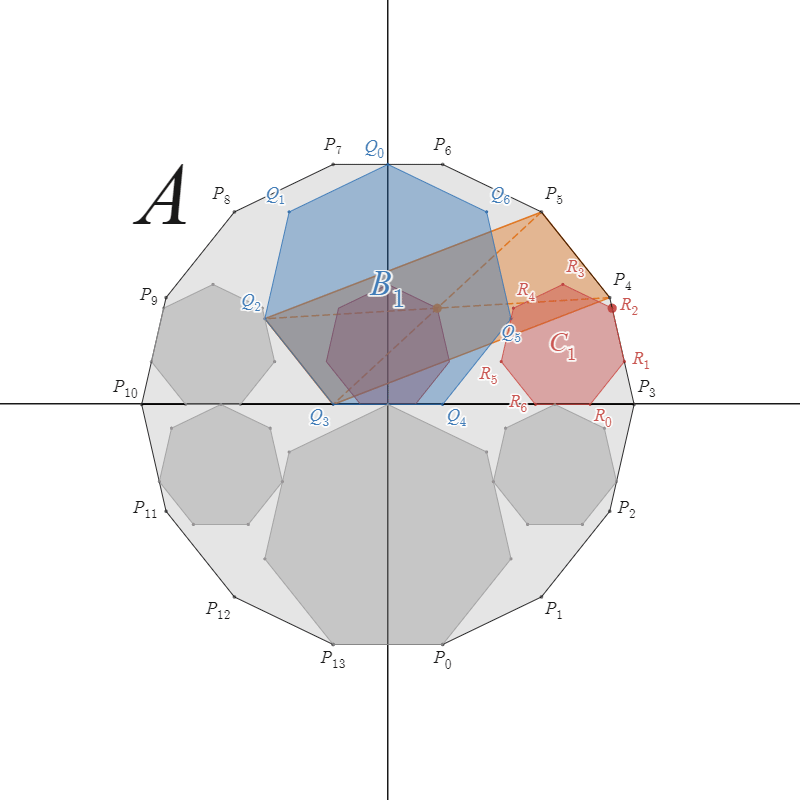説明用

$A,B,C$ それぞれの中心から頂点までの距離を $r_A,r_B,r_C$ とする。
$r_A,r_B,r_C$ を $n,k$ で表すと

　　　　$r_A=\dfrac{4\cos\frac{\pi}{2n}}{\sin\frac{\pi}{n}}, r_B=\dfrac{2}{\sin\frac{\pi}{n}}, r_C=\dfrac{1}{\sin\frac{\pi}{n}}$

となる。
$C_1$ の $x$ 座標を $x_C$ とすると、$P_k,Q_k,R_k$ の座標は次のように書くことができる。

　　$P_k=\left(r_A \sin\dfrac{\pi(2k+1)}{2n},-r_A \cos\dfrac{\pi(2k+1)}{2n} \right)$

　　$Q_k=\left(-r_B \sin\dfrac{2\pi k}{n},r_B\cos\dfrac{\pi}{n}+r_B \cos\dfrac{2\pi k}{n} \right)$

　　$R_k=\left(x_C + r_C \sin\dfrac{\pi (2k+1)}{n},r_C\cos\dfrac{\pi}{n}-r_C \cos\dfrac{\pi (2k+1)}{n} \right)$

$Q_k,Q_{k+1},P_{2k},P_{2k+1}$ を頂点とする平行四辺形の対角線の交点は、$Q_k$ と $P_{2k}$ の中点であるから、その座標を $M_k$ とすると

${\displaystyle \begin{align} M_k=\left( \frac{-r_B \sin\frac{2\pi k}{n} +r_A \sin\frac{\pi(4k+1)}{2n} }{2}, \frac{r_B\cos\frac{\pi}{n}+r_B \cos\frac{2\pi k}{n} -r_A \cos\frac{\pi(4k+1)}{2n} }{2} \right) \end{align} }$

となる。$k$ が変化すると、各三角関数の位相が$\dfrac{2\pi k}{n}$ ずつ変化することから、三角関数を合成して
${\displaystyle \begin{align} M_k=\left( r\sin\left(\alpha+\frac{2\pi k}{n} \right), \frac{r_B\cos\frac{\pi}{n}}{2} -r\cos\left(\alpha+\frac{2\pi k}{n} \right) \right) \end{align} }$

と表すことができることがわかる。
$r,\alpha$を具体的に求める。

$k=\dfrac{n-1}{2}$のとき

${\displaystyle \begin{align} M_{\frac{n-1}{2}}&=\left( \frac{-r_B \sin\frac{\pi (n-1))}{n} +r_A \sin\frac{\pi(2n-1)}{2n} }{2}, \frac{r_B\cos\frac{\pi}{n}+r_B \cos\frac{\pi (n-1)}{n} -r_A \cos\frac{\pi(2n-1)}{2n} }{2} \right) \\ &=\left( \frac{-r_B \sin\frac{\pi}{n} +r_A \sin\frac{\pi}{2n} }{2}, \frac{r_B\cos\frac{\pi}{n}-r_B \cos\frac{\pi}{n} +r_A \cos\frac{\pi}{2n} }{2} \right) \\ &=\left( \frac{-r_B \sin\frac{\pi}{n} +2r_B\cos\frac{\pi}{2n} \sin\frac{\pi}{2n} }{2}, \frac{r_B\cos\frac{\pi}{n}-r_B \cos\frac{\pi}{n} +2r_B\cos\frac{\pi}{2n} \cos\frac{\pi}{2n} }{2} \right) \\ &\qquad \because r_A = 2r_B\cos\frac{\pi}{2n}\\ &=\left( \frac{-r_B \sin\frac{\pi}{n} +r_B\sin\frac{\pi}{n} }{2}, \frac{r_B\cos\frac{\pi}{n}-r_B \cos\frac{\pi}{n} +r_B(1+\cos\frac{\pi}{n}) }{2} \right) \\ &=\left( 0, \frac{r_B\cos\frac{\pi}{n} }{2} +\frac{r_B}{2} \right) \\ \end{align} }$

であるから、
　　　　$r=\dfrac{r_B}{2},\alpha=\dfrac{\pi}{n} $

であるとわかる。
代入すると

　　　　${\displaystyle \begin{align} M_k&=\left( r\sin\left(\alpha+\frac{2\pi k}{n} \right), \frac{r_B\cos\frac{\pi}{n}}{2} -r\cos\left(\alpha+\frac{2\pi k}{n} \right) \right)\\ &=\left( \dfrac{r_B}{2}\sin\left(\dfrac{\pi}{n}+\frac{2\pi k}{n} \right), \frac{r_B\cos\frac{\pi}{n}}{2} -\dfrac{r_B}{2}\cos\left(\dfrac{\pi}{n}+\frac{2\pi k}{n} \right) \right)\\ &=\left( r_C\sin\left(\dfrac{\pi(2k+1)}{n} \right), r_C\cos\frac{\pi}{n} -r_C\cos\left(\dfrac{\pi(2k+1)}{n} \right) \right)\\ &\qquad\because r_B = 2r_C \end{align} }$

となる。

したがって、$M_k$ を順につなぐと、一辺の長さが $1$ の正 $n$ 角形を描くことがわかる。
さらに、

　　$R_k=\left(x_C + r_C \sin\dfrac{\pi (2k+1)}{n},r_C\cos\dfrac{\pi}{n}-r_C \cos\dfrac{\pi (2k+1)}{n} \right)$

であるから、$M_k$ と $R_k$ の $y$ 座標は一致することがわかる。

次に、$k$ を $0$ から順に $1$　つずつ大きくしていくことを考えます。

$k$ を１つずつ大きくする

最初のうちは

　　$Q_{k+1}$ の $y$ 座標 $\ge$ $P_{2k+1}$ の $y$ 座標

となっていますが、途中から大小関係が逆転して

　　$Q_{k+1}$ の $y$ 座標 $\lt$ $P_{2k+1}$ の $y$ 座標

となる $k$ が必ず存在します。最初に大小関係が逆転するときの $k$ を特に $k_0$ と書くことにします。
さて、ここから$Q_{k_0}$ の $y$ 座標と $P_{2k_0}$ の $y$ 座標の大小関係により場合分けが発生します。

《パターン$1$》$Q_{k_0}$ の $y$ 座標 $\gt$ $P_{2k_0}$ の $y$ 座標の場合

例えば $n=9$ の場合がこのパターンになります。

《パターン$1$》の例　正9角形の場合

ここからは説明の都合上、$P,Q,R$ の各点について、左右を入れ替えたものを$P',Q',R'$と表記することにします。式の形で表すと

　　$P'_k=P_{2n-1-k},Q'_k=Q_{n-k},R'_k=R_{n-1-k}$

ということです。
平行四辺形の各頂点の $y$ 座標の大小関係と、$R_{k_0},R'_{k_0}$ の $y$ 座標が平行四辺形の対角線の交点の $y$ 座標と一致するという事実から、

($Q'_{k_0+1}$ の $y$ 座標) $\lt$ ($R'_{k_0}$ の $y$ 座標) $\lt$ ($Q'_{k_0}$ の $y$ 座標)

であることがわかり、また、$R'_{k_0}$ をはさむ $C_1$ の辺の角度を考えれば、$C_1$ は頂点 $R'_{k_0}$ で $B_1$ に外接していることが分かります。

さらに、次の事実がわかります。

($P_{2k_0}$ の $y$ 座標) $\lt$ ($R_{k_0}$ の $y$ 座標) $\lt$ ($P_{2k_0+1}$ の $y$ 座標)

これで、「$R_{k_0}$ の $y$ 座標が $P_{2k_0}$ の $y$ 座標と $P_{2k_0+1}$ の$y$ 座標の間にある」ことが示されましたが、まだ、$C_1$ と $A$ が接していることを証明したことにはならないことに注意してください。

次に、$R_{k_0}$ が直線 $P_{2k_0}P_{2k_0+1}$ 上にあることを示します。

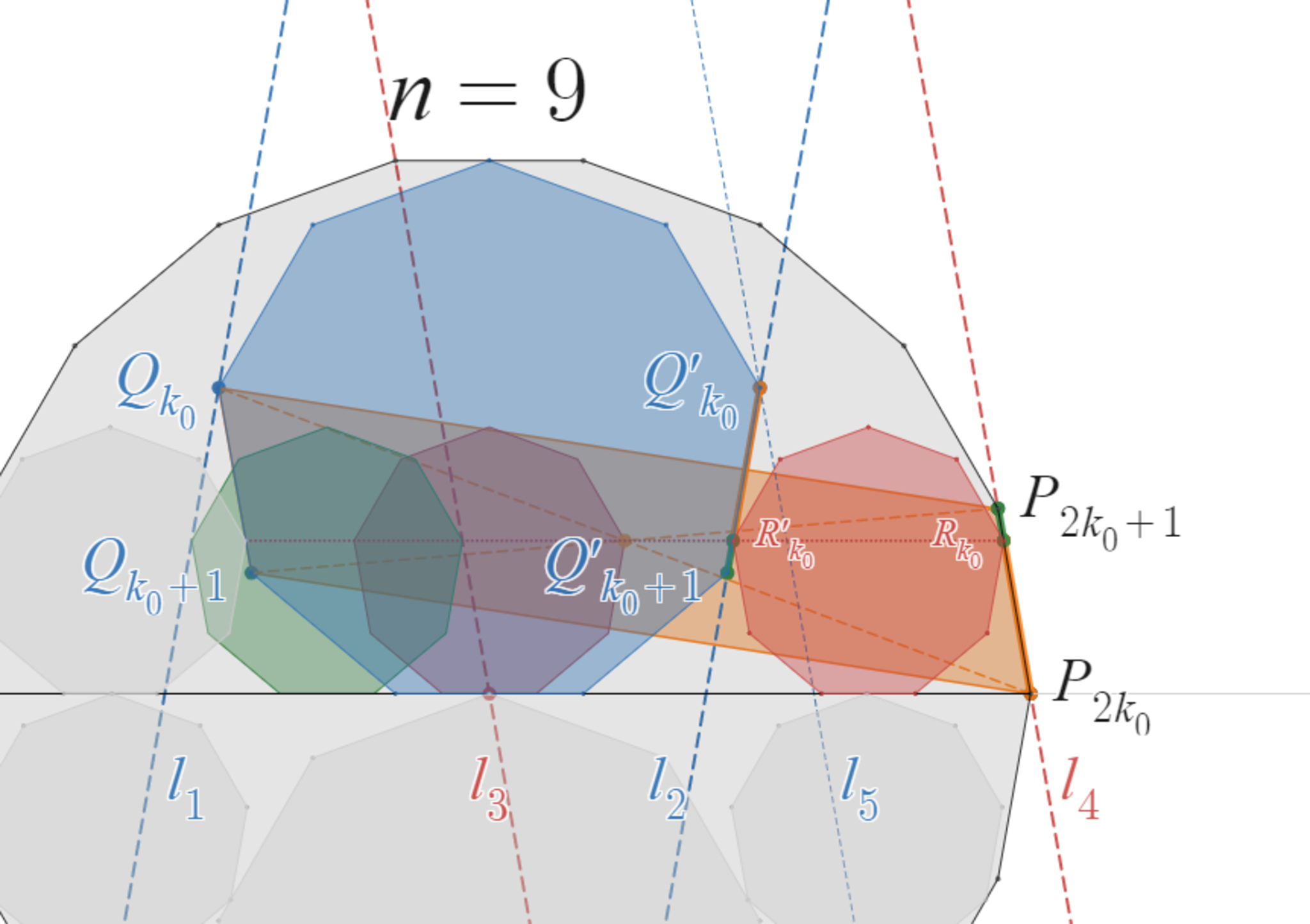補助線となる平行線を引く

　$Q_{k_0},Q'_{k_0}$ を通り辺 $Q'_{k_0}Q'_{k_0+1}$ と平行な直線 $l_1,l_2$ を引きます。
　原点$,P_{2k_0},Q'_{k_0}$ を通り辺 $P_{2k_0}P_{2k_0+1}$ と平行な直線 $l_3,l_4,l_5$ を引きます。
　
　$x$ 軸$,l_1,l_5$ で囲まれた三角形と、$x$ 軸$,l_1,l_3$ で囲まれた三角形は相似になっていて、相似比は $2:1$ ですから、後者の三角形の中に $C$ と合同な正 $n$ 角形を内接させることができます。図中の緑色の正 $n$ 角形がそれです。

　$l_3$ と　$l_4$ (赤線)　の距離は、$B$ を挟む直線間の距離と同じですから、$l_1$ と　$l_2$ (青線)　の距離と同じです。($B$ が $x$ 軸と $A$ の一番上の辺に挟まれているのを見ていただければわかると思います。)

　そのため、$x$ 軸$,l_1,l_3$ で囲まれた三角形と、$x$ 軸$,l_2,l_4$ で囲まれた三角形は合同です。したがって、$C$ と $l_4$ が接していることがわかります。
　補題$4$　と、$C_1$ の頂点 $R_{k_0}$ を挟む辺の角度から、$C_1$ が頂点 $R_{k_0}$ で $A$ の辺 $P_{2k_0}P_{2k_0+1}$ に内接していることが言えました。

系

　また、次の興味深い関係も得られます。

$R_{k_0}P_{2k_0}=R'_{k_0}Q'_{k_0}$

$R_{k_0}P_{2k_0+1}=R'_{k_0}Q'_{k_0+1}$

図中のオレンジ線と緑線の部分の長さがそれぞれ等しいということです。
美しい関係だと思いませんか?

($P_{2k_0+1}$ の $y$ 座標) - ($R_{k_0}$ の $y$ 座標) = ($R'_{k_0}$ の $y$ 座標) - ($Q'_{k_0+1}$ の $y$ 座標)

($R_{k_0}$ の $y$ 座標) - ($P_{2k_0}$ の $y$ 座標) = ($Q'_{k_0}$ の $y$ 座標) -($R'_{k_0}$ の $y$ 座標)

より明らか。

《パターン$2$》$Q_{k_0}$ の $y$ 座標 $\le$ $P_{2k_0}$ の $y$ 座標の場合

例えば $n=7$ の場合がこのパターンになります。

《パターン$2$》の例　正7角形の場合

先ほどと同様、平行四辺形の頂点と対角線の交点の $y$ 座標を比較することにより、

($R'_{k_0-1}$ の $y$ 座標) $\leq$ ($Q'_{k_0}$ の $y$ 座標) $\lt$ ($R'_{k_0}$ の $y$ 座標)

であることがわかり、また、$Q'_{k_0}$ をはさむ $B_1$ の辺の角度を考えれば、$B_1$ は頂点 $Q'_{k_0}$ で $C_1$ に外接していることが分かります。

さらに、次の事実がわかります。

($P_{2k_0-1}$ の $y$ 座標) $\leq$ ($R_{k_0-1}$ の $y$ 座標) $\lt$ ($R_{k_0}$ の $y$ 座標) $\lt$ ($P_{2k_0}$ の $y$ 座標)

これで、「$R_{k_0-1},R_{k_0}$ の $y$ 座標が $P_{2k_0-1}$ の $y$ 座標と $P_{2k_0}$ の$y$ 座標の間にある」ことが示されましたが、まだ、$C_1$ と $A$ が接していることを証明したことにはならないことに注意してください。

次に、$R_{k_0-1},R_{k_0}$ が直線 $P_{2k_0-1}P_{2k_0}$ 上にあることを示します。

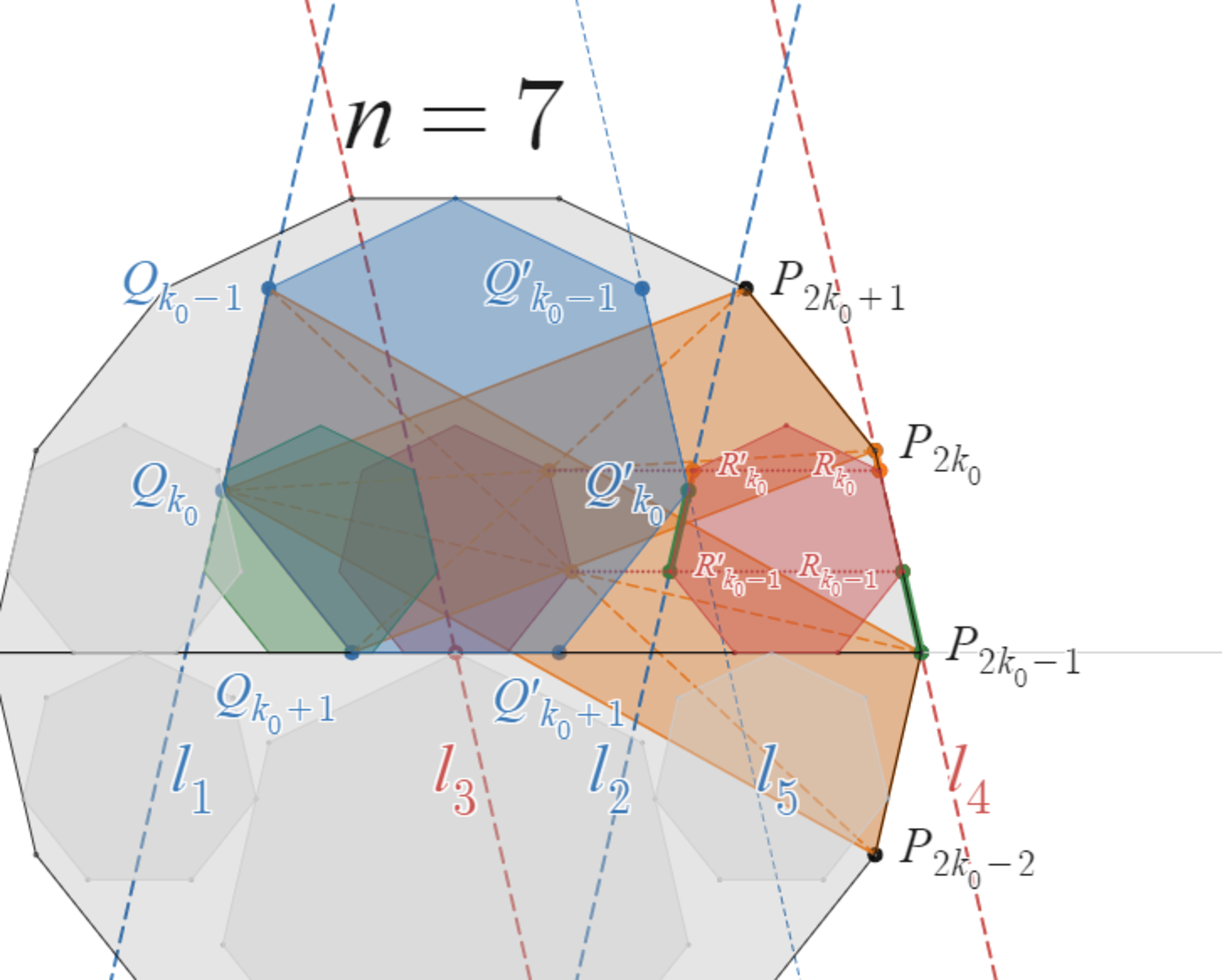補助線となる平行線を引く

　補助線 $l_1,l_2,l_3,l_4,l_5$ の引き方は先ほどと同様です。
　$x$ 軸$,l_1,l_3$ で囲まれた三角形と、$x$ 軸$,l_2,l_4$ で囲まれた三角形は合同です。したがって、$C$ と $l_4$ が接していることがわかります。
　補題$6$　から、$C_1$ が辺 $R_{k_0-1}R_{k_0}$ で $A$ の辺 $P_{2k_0-1}P_{2k_0}$ に内接していることが言えました。

系

　また、次の興味深い関係も得られます。

$R_{k_0}P_{2k_0}=R'_{k_0}Q'_{k_0}$

$R_{k_0-1}P_{2k_0-1}=R'_{k_0-1}Q'_{k_0}$

図中のオレンジ線と緑線の部分の長さがそれぞれ等しいということです。
これまた美しい関係だと思いませんか?

下半分の証明

下半分の証明は、上半分の証明と全く同じ方法で行うことができます。ここでは補助線だけ提示しておきます。

補助線たち

正"偶数"角形の場合の証明

　正偶数角形の場合も、ほぼ同様の手順で証明できます。

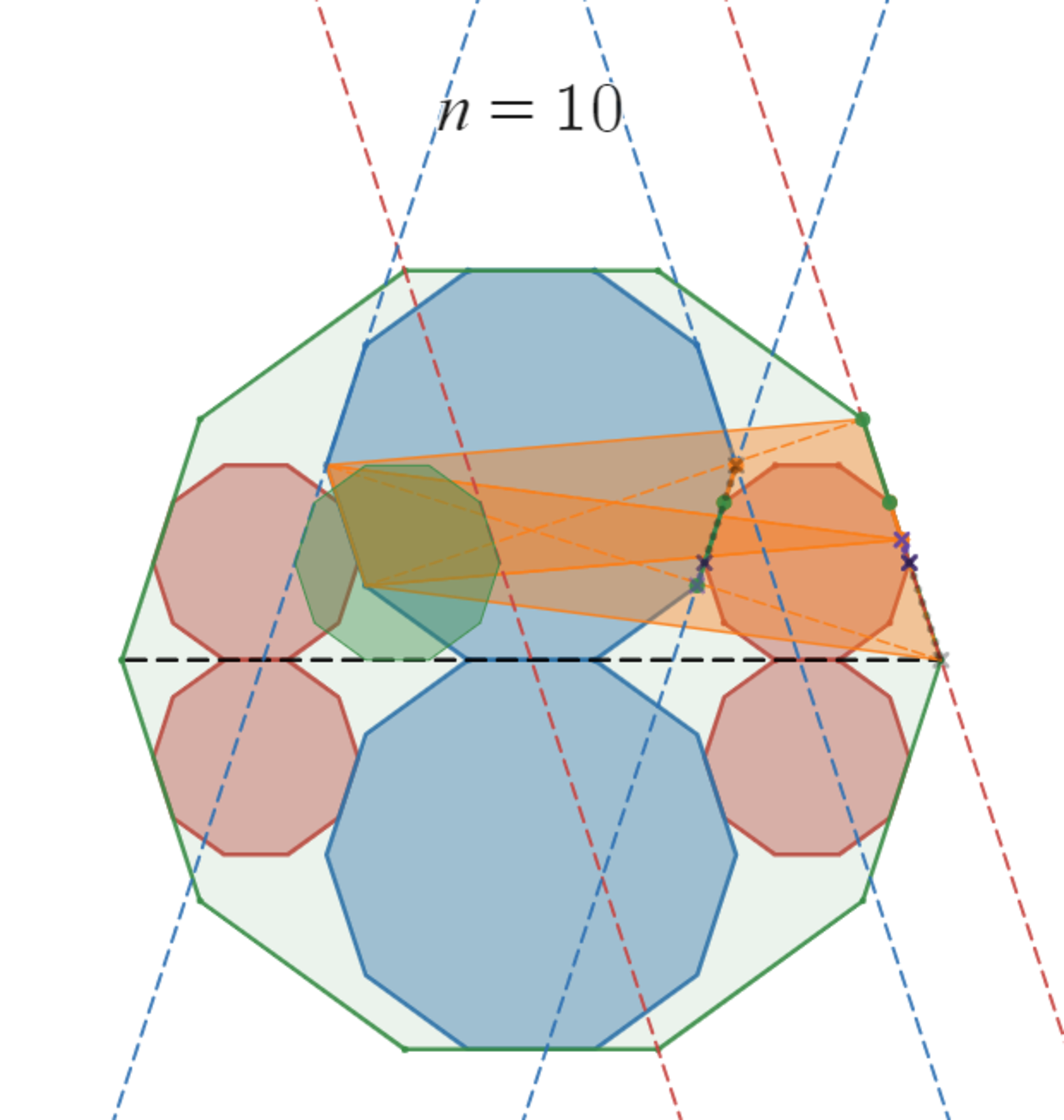正10角形の場合の補助線

平行四辺形を使うために、外側の正 $n$ 角形の辺の中点を使うところが正奇数角形のときとは違いますが、後は同じ方法で証明できます。

　正$12$角形の場合の補助線はこんな感じになります。

正$12$角形の場合の補助線

偶数バージョンの方は途中で力尽きた感じになってしまいましたが、いったんここで終了とさせていただきたいと思います。

Twitter に集められた情報

今回のこの超面白い性質の発見と証明には、Twitterでたくさんの方の協力をいただきました。証明に直接貢献された皆さんのツイートをここでまとめて紹介したいと思います。そのほかにも、この問題をたくさんの方に考えていただきました。本当にありがとうございました。

Leukocyte (@insanity_EX)
ａｐｕ (@apu_yokai)
Diego Rattaggi 🇨🇭(@diegorattaggi)
じゃがりきん(@jagarikin)
立見鶏(@StandeeCock)
Makoto Kamada(@kamadox)
獅子座じゃない人@メiドi1i最i下i位i作i品iのi作i者(@leo_maru_gt)
ますたぁP@ポップン(4)(@0625Master)

おわりに

　今回は本当にたくさんの方のご協力でこの面白い性質を発見、証明することができました。Twitterで数学で遊んでいて本当に良かったと思います。これからもいろいろ遊んでいきたいと思っています。今後ともよろしくお願いします!

　また、記事の内容に関連する情報等ありましたらどんどん教えてくださいね。

(2022.08.15)追記

　この記事で紹介した正多角形の性質について、更に驚くべき一般化が可能であることが分かりました!
　是非、下のリンクから記事をご覧いただきたいと思います。

Mathlog:相似比2:1の正多角形内接の定理の驚くべき一般化

投稿日：2022年7月18日

更新日：2022年8月15日

投稿者

apu_yokai

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

apu_yokai

相似比2:1の正多角形内接の定理