相似比2:1の正多角形内接の定理の驚くべき一般化
はじめに
前回投稿した「相似比2:1の正多角形内接の定理」の記事はおかげさまで大好評でした。
実際、とても面白い性質を見つけることができたと思っていました。
しかし、それは実は、もっと面白い性質のほんの一瞬を切り取ったものにすぎなかったのです!
そのことを発見したときは本当に驚きました。
そのときの感動を少しでも記事に表現することができればと思います。
この記事では、その性質を紹介し、さらに証明にも挑戦します。
少し長くなると思いますが、お急ぎの方は「もっと面白い性質」の部分だけでもご覧いただければ幸いです。
前回の記事で証明したこと
まずは前回の記事で証明した定理を再掲します。
$n$ を $3$ 以上の奇数又は $4$ 又は $6$ とする。
$xy$ 座標平面上の原点を中心とし、辺の一つが $x$ 軸と平行になるように一辺の長さ $2$ の正 $2n$ 角形 $A$ を配置する。
$y$ 軸上に中心をもち、中心より下にある辺の一つが $x$ 軸と平行、かつ一辺の長さ $2$ の正 $n$ 角形 $2$ つを、$A$ に内接しかつ $x$ 軸と接するように配置する。それらのうち中心の $y$ 座標が正のものを $B_1$、負のものを$B_2$とする。
このとき、$B_1$又は$B_2$と外接し、かつ $x$ 軸とも接するように、「中心より下にある辺の一つが $x$ 軸と平行、かつ一辺の長さ $1$ の正 $n$ 角形 $C$ 」を配置すると、$C$ は必ず $A$ に内接する。
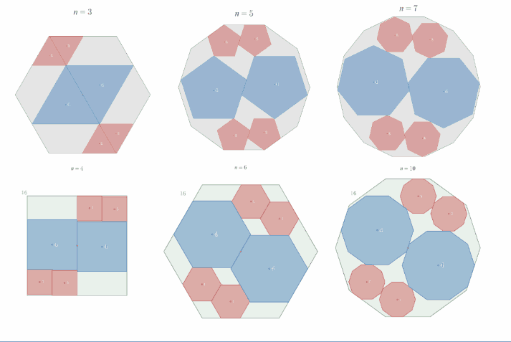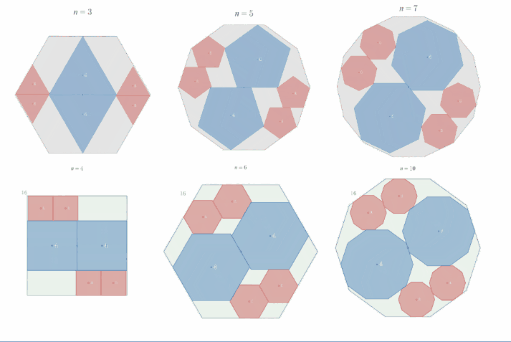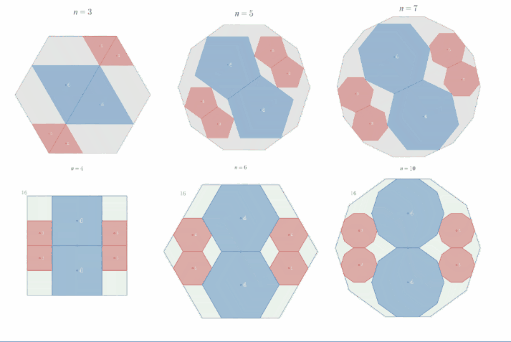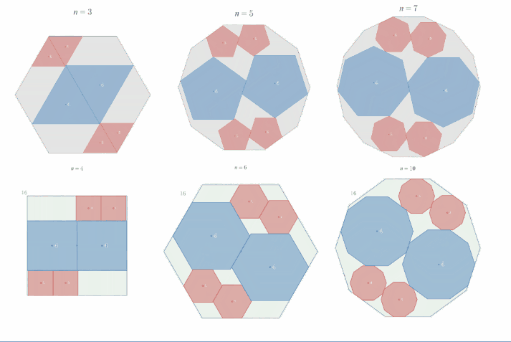
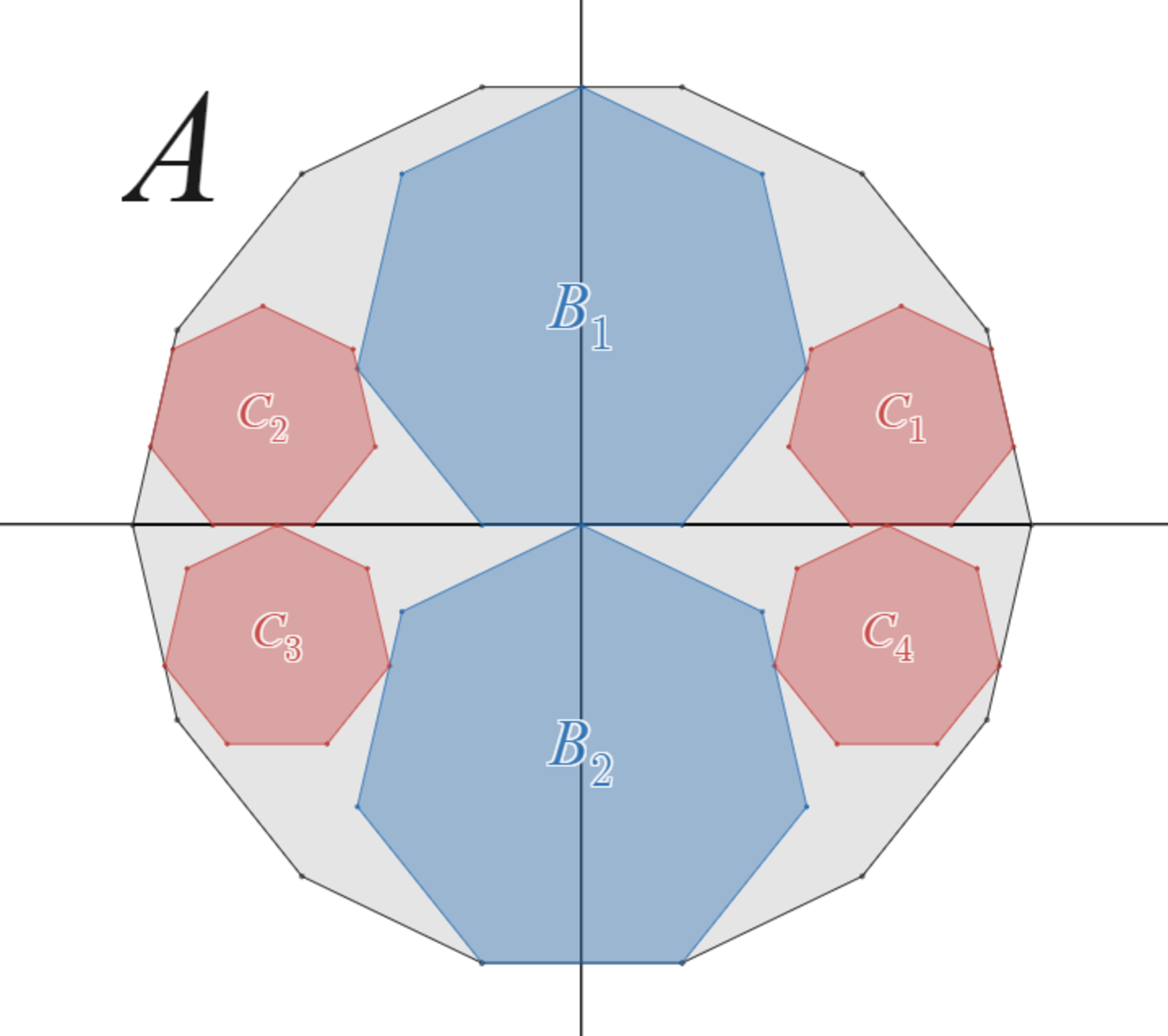 相似比2:1の正"奇数"角形内接の定理
相似比2:1の正"奇数"角形内接の定理
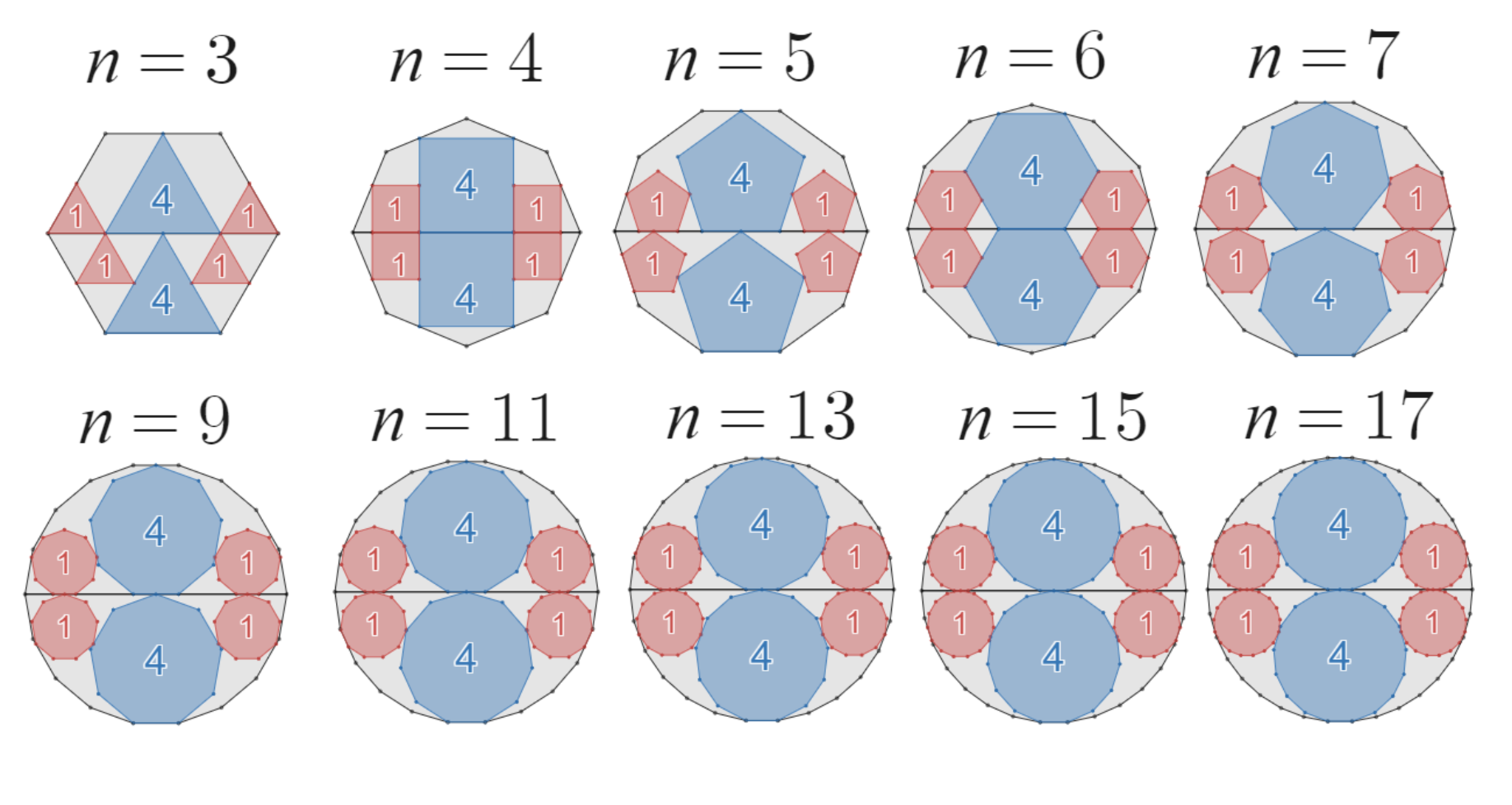 具体例
具体例
$n$ を $2$ 以上の偶数とする。
$xy$ 座標平面上の原点を中心とし、辺の一つが $x$ 軸と平行になるように一辺の長さ $4$ の正 $n$ 角形 $A$ を配置する。
$y$ 軸上に中心をもち、辺の一つが $x$ 軸と平行、かつ一辺の長さ $2$ の正 $n$ 角形 $2$ つを、$A$ に内接しかつ $x$ 軸と接するように配置する。それらのうち中心の $y$ 座標が正のものを $B_1$、負のものを$B_2$とする。
このとき、$B_1$又は$B_2$と外接し、かつ $x$ 軸とも接するように、「辺の一つが $x$ 軸と平行、かつ一辺の長さ $1$ の正 $n$ 角形 $C$ 」を配置すると、$C$ は必ず $A$ に内接する。
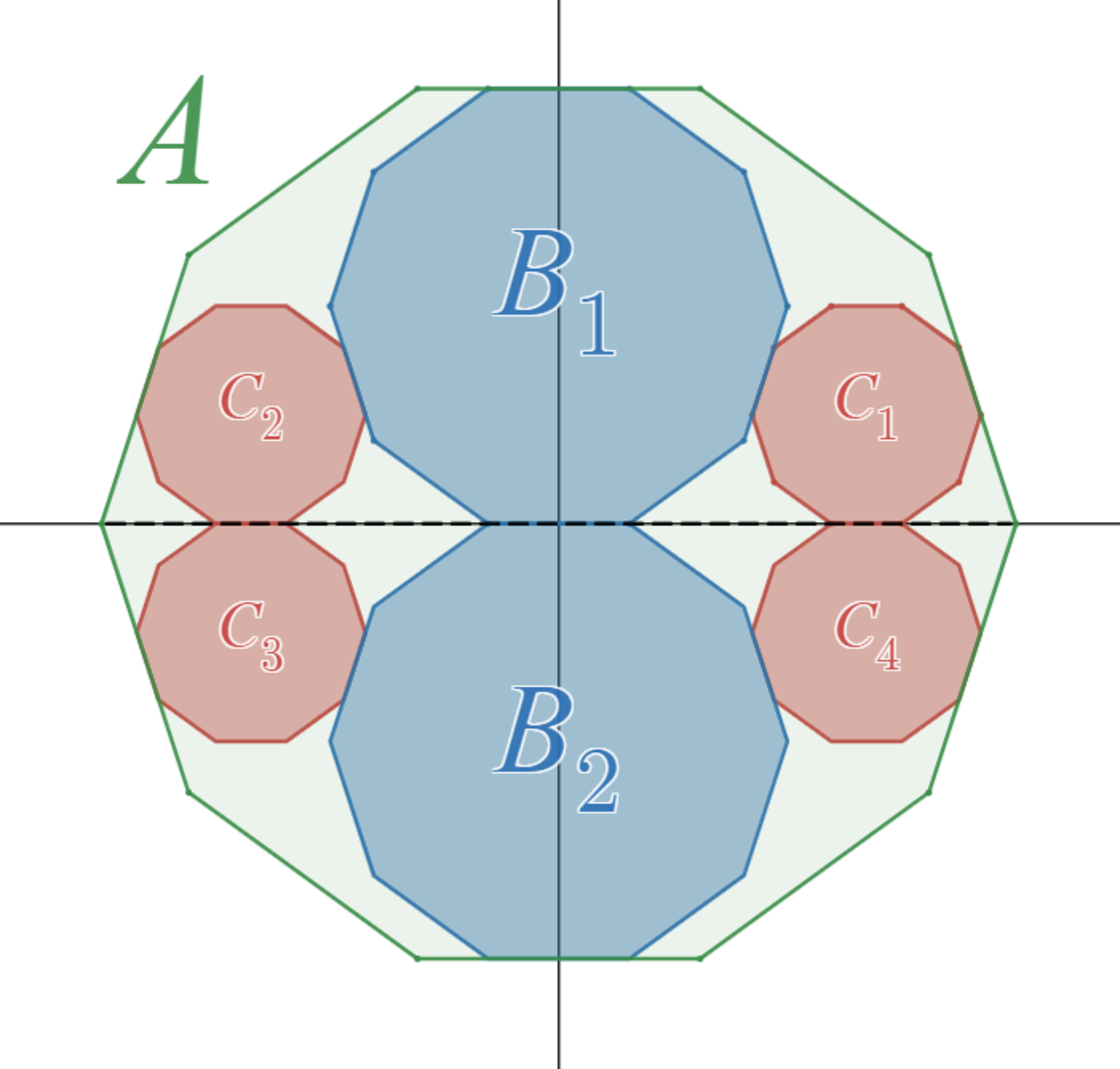 相似比2:1の正"偶数"角形内接の定理
相似比2:1の正"偶数"角形内接の定理
 具体例
具体例
一般化への道
相似比2:1の正"偶数"角形内接の定理の一般化可能性の発見
「もっと面白い性質」の発見のきっかけとなったのは、ますたぁP@ポップン(4) (@0625Master)さんのこれらのツイートでした。
これの定理2【相似比2:1の正"偶数"角形内接の定理】について、正n角形を全てπ/nずつ傾けたものについても成り立ちそうだということを見つけました
— ますたぁP@ポップン(4) (@0625Master) July 26, 2022
真上に頂点がくるように全ての正n角形を配置しても成り立つという感じです
まだ……終わらないのか!? https://t.co/tW6dMb4kT9
当然、こういう疑問が湧く
— ますたぁP@ポップン(4) (@0625Master) July 26, 2022
π/n傾けても成り立つんなら実は任意の角度傾けても成り立つのでは?
試してみると、確かに真上に頂点がくるように全ての正n角形を配置しても同様の配置にできることがわかりました。
 頂点が上になるようにしても成立する
頂点が上になるようにしても成立する
そして、さらなる一般化・・・すなわち、任意の角度で同様の配置が可能なのではないか、という重要な予想がされました。
実は、当初私は「さすがにそれは無理では?」と考えていたのですが・・・
さすがにこれは無理…な気がします🤔 https://t.co/KJiNW5StZF pic.twitter.com/T919000zyX
— apu (@apu_yokai) July 26, 2022
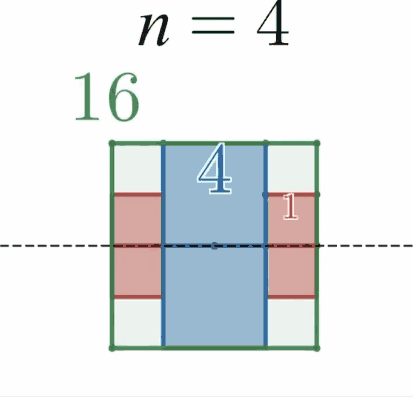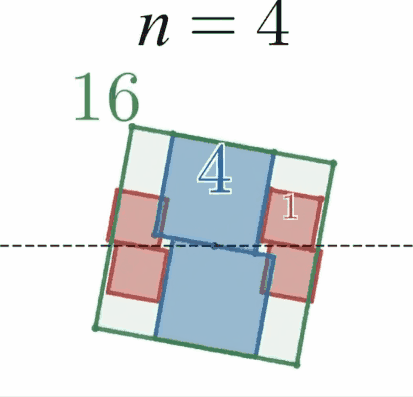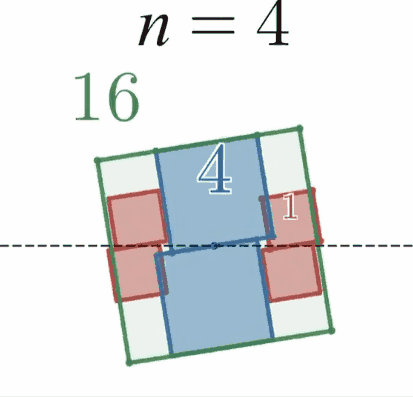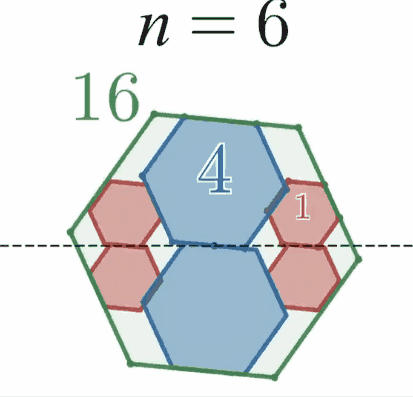 試行錯誤の様子
試行錯誤の様子
しばらく考えていたところ、
「スライドパズルのように各パーツをシンクロさせながら平行移動することで少しずつ位置を回転できるのでは?」
「仮にスライドパズルのように各パーツの位置を一周させることができたなら、その状態をベースに、$B_1,B_2$ の中心が $y$ 軸上に来るように回転させれば、一般化が可能なのでは?」
というヒラメキが訪れました。
実際にやってみると、直感どおり、各パーツをシンクロさせながら平行移動することで少しずつ位置を回転させることも、その状態をベースに、$B_1,B_2$ の中心が $y$ 軸上に来るように回転させることで一般化することも可能だったのです!
相似比2:1の正"偶数"角形内接の定理の一般化
それではご覧ください。これが任意の角度に一般化された「相似比2:1の正"偶数"角形内接の定理」の姿です!
 相似比2:1の正"偶数"角形内接の定理の一般化
相似比2:1の正"偶数"角形内接の定理の一般化
(相似比2:1の正"奇数"角形内接の定理)の一般化
「正"偶数"角形でできたんなら、正"奇数"角形でもできるのでは?」というのは自然な発想ではないでしょうか。偶数の場合は上下対象ですが、奇数の場合は上下対象ではないので、一見うまくいかなさそうに思えます。
・・・が、試行錯誤を続けた結果、「上半分と下半分の向きを逆にすれば、同じことができる」ということを発見しました!
これが任意の角度に一般化された「相似比2:1の正"奇数"角形内接の定理」の姿です!
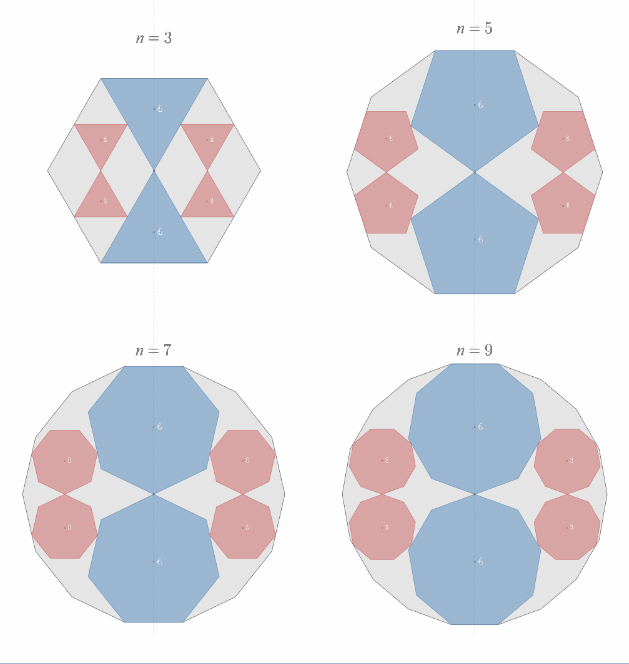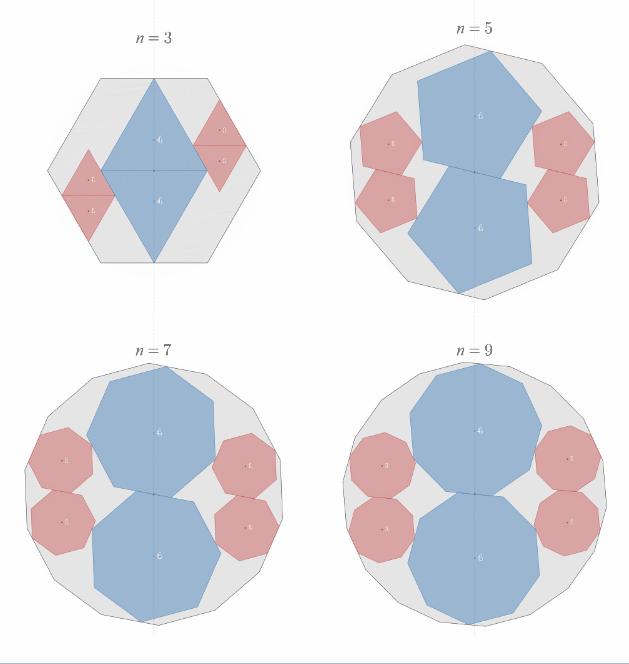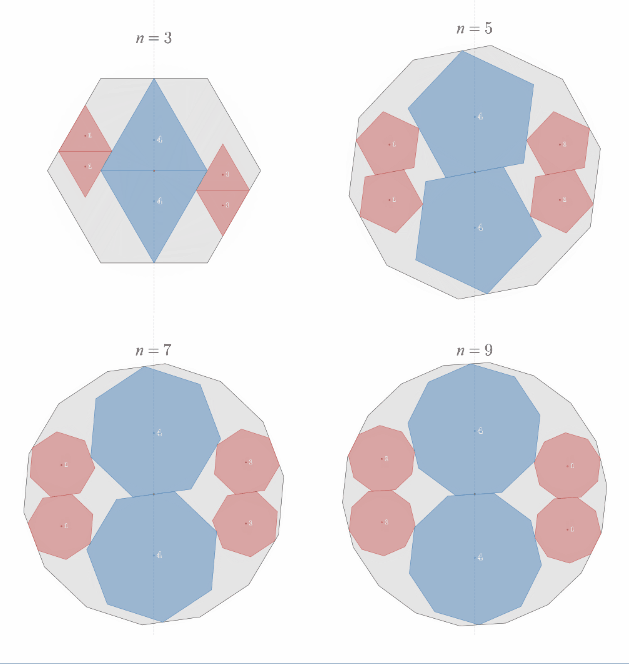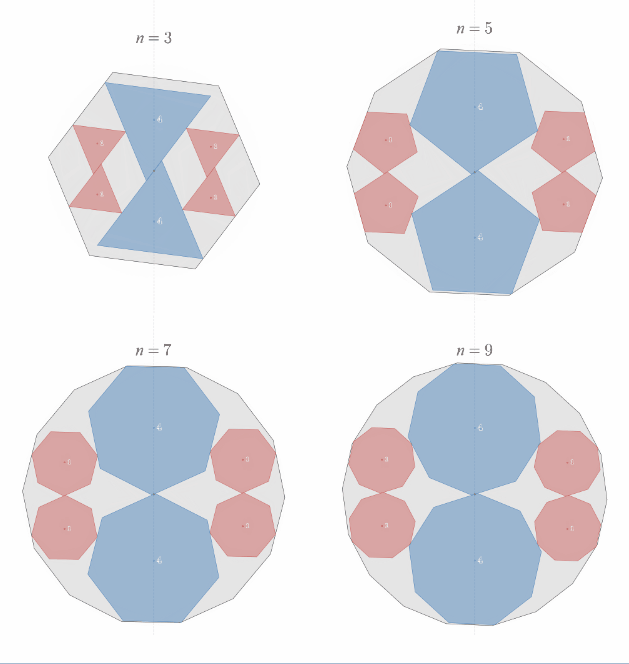 相似比2:1の正"奇数"角形内接の定理の一般化
相似比2:1の正"奇数"角形内接の定理の一般化
定理っぽく表現するとこんな感じでしょうか。
「相似比2:1の正"偶数"角形内接の定理」又は「相似比2:1の正"奇数"角形内接の定理」の配置を基準とする。ただし、"奇数"の場合は、$B_2,C_3,C_4$ の位置と角度をそれぞれ $B_1,C_2,C_1$ の $x$ 軸に対する鏡像の位置に変更したものとする。
基準の位置から始めて、$B_1,B_2,C_1,C_2,C_3,C_4$各パーツが互いに外接している状態を保ちつつ、かつ各パーツが $A$ に内接したまま平行移動することで、各パーツを原点の周りに一周させることができる。
一周させる間、$B_1,B_2$ と原点は常に一直線上にあるから、その直線と$B_1$(又は$B_2$)の辺のなす角度を任意の角度にすることができる。
(文章にしてしまうと意味不明な感じになってしまいますが)いやあ、これは美しいですね!
前回の記事が、この美しい関係のほんの一瞬を切り取った姿にすぎないことがお判りいただけましたでしょうか。
とはいえ、前回証明した定理がなければこの美しい性質を証明することは(私には)できません。
前回証明した定理により、その「一瞬」の状態が可能であることは証明済ですので、あとは、その「一瞬」の状態からスムーズに1回転させることが可能であることだけを証明すればよいことになります。
証明
スライドパズルのように
それではここから証明パートに入りたいと思います。
証明しやすいように、ここからは一番大きい正多角形を固定します。
そして、その内部を大小の正 $n$ 角形がスライドパズルのようにシンクロした平行移動を繰り返すことで1回転できることを示します。
 スライドパズルのような平行移動で1回転させることができることを示したい
スライドパズルのような平行移動で1回転させることができることを示したい
正"奇数"角形の場合の証明(導入)
なるべく場合分けはしたくないのですが、最小限の場合分けは必要です。
まず、正"奇数"角形の場合の証明をします。
各パーツが内部を $1$ 回転する間に同じ動きを $n$ 回繰り返すわけですから、$\frac{1}{n}$ 回転分だけを証明すればよいですね。
$\frac{1}{n}$ 回転分を区切って考えるにあたり、一番考えやすいところで区切ることにします。下図をご覧ください。
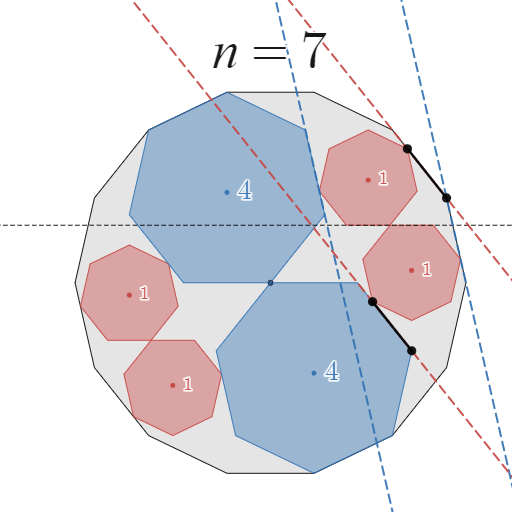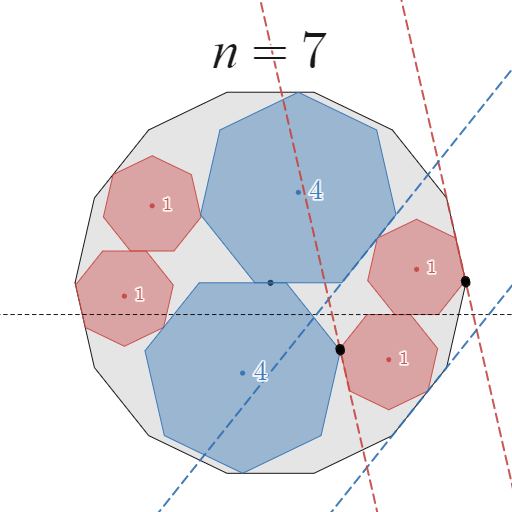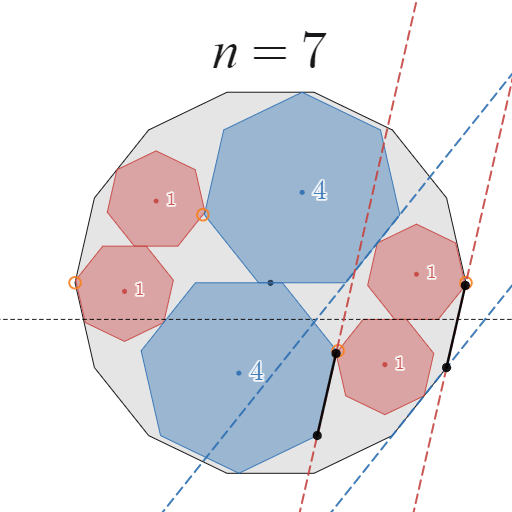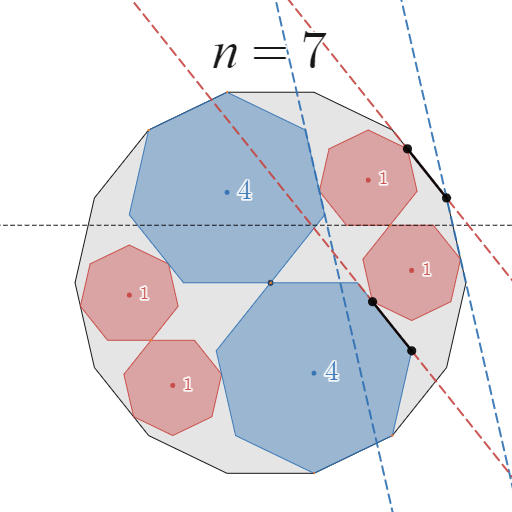 この動きが可能であることを証明すればよい
この動きが可能であることを証明すればよい
具体的には、$B_1$ の正 $n$ 角形が $x$ 軸上をスライドするように移動する部分を$\frac{1}{n}$ 回転分の部分として区切ることにします。
($B_1$ などの記号は上記の定理と同様の位置にある正多角形と考えてください。以下同様です。)
このとき、$B_1$ の頂点のうち $A$ と接する頂点は $\frac{1}{2n}$ 回転分しか移動していないように見えますが、次の移動のときには隣の頂点が $A$ と接触するため、この動きを $n$ 回繰り返すと $1$ 回転となることを確認してください。
実際、全体として移動前と移動後の位置は時計回りにちょうど$\frac{1}{n}$ 回転した位置になっていますね。
もう少し細かく分析しましょう。
$B_1$ と $B_2$ の接触する辺と、$C_1$ と $C_4$ の接触する辺はいずれも $x$ 軸に平行となっています。
$B_1$ と $B_2$ は移動方向は一定ですが、$C_1$ と $C_4$ は、それぞれ $2$ 回ずつ方向を変えています。
$C_1$ と $C_4$ の移動方向は変わりますが、その $y$ 座標に注目すると、境界線が $x$ 軸に平行ですから、$C_1$ と $C_4$ の $y$ 座標の変位は同じ です。
赤い線と青い線が $2$ 本ずつあります。
右側の赤線と青線は、それぞれ $C_1$と $A$ 、 $C_4$ と $A$ が接触する位置にあります。
左側の赤線と青線は、それぞれ $C_4$と $B_2$ 、 $C_1$ と $B_1$ が接触する位置にあります。
どうやら、赤線どおし、青線どおしはそれぞれが同じタイミングで角度が変わり、常に平行になっているように見えます。
もし、本当に同じタイミングで角度が変わっているのであれば、$C_1$ と $C_4$ の $y$ 座標の変位は同じであることから、「左側の青線が $x$ 軸正の方向へ移動した距離」と「左側の赤線が $x$ 軸負の方向へ移動した距離」が一致することになります
各正 $n$ 角形の $x$ 座標にも注目してみましょう。赤線どおし、青線どおしそれぞれが同じタイミングで角度が変わっているのであれば、$B_1$ の $x$ 座標が $x_{b1}$ 増加し、$C_1$ の $x$ 座標が $x_{c1}$ 増加したとき、$C_4$ の $x$ 座標は $x_{b1}-x_{c1}$ 減少し、$B_2$ の $x$ 座標が $x_{b1}$ 減少することから、$B_1,B_2$ の $x$ 座標の差は $2x_{b1}$ 、$C_1,C_4$ の $x$ 座標の差は $x_{b1}$ となります。つまり、「** $B_1,B_2$ の $x$ 座標の差は、$C_1,C_4$ の $x$ 座標の差の $2$ 倍**」ということです。
以上から、赤線どおし、青線どおしそれぞれが同じタイミングで角度が変わっているのであれば全体としてこのような動きが可能であるとわかります。
したがって、証明すべきことは「赤線どおし、青線どおしはそれぞれが同じタイミングで角度が変わり、常に平行になっていること」となります。
赤線どおし、青線どおしはそれぞれが同じタイミングで角度が変わり、常に平行になっていること
さて、ここからさらに場合分けをします。
移動前の配置(移動後の配置でも同じ)において、$C_1$ が $A$ と「頂点で接触するか、辺で接触するか」の $2$ パターンそれぞれについて考えます。
正"奇数"角形の場合の証明(頂点接触の場合)
まずは移動前の配置で $C_1$が $A$ と「頂点で接触する」場合について考えます。例えば、$n=7$ のときは頂点で接触しています。
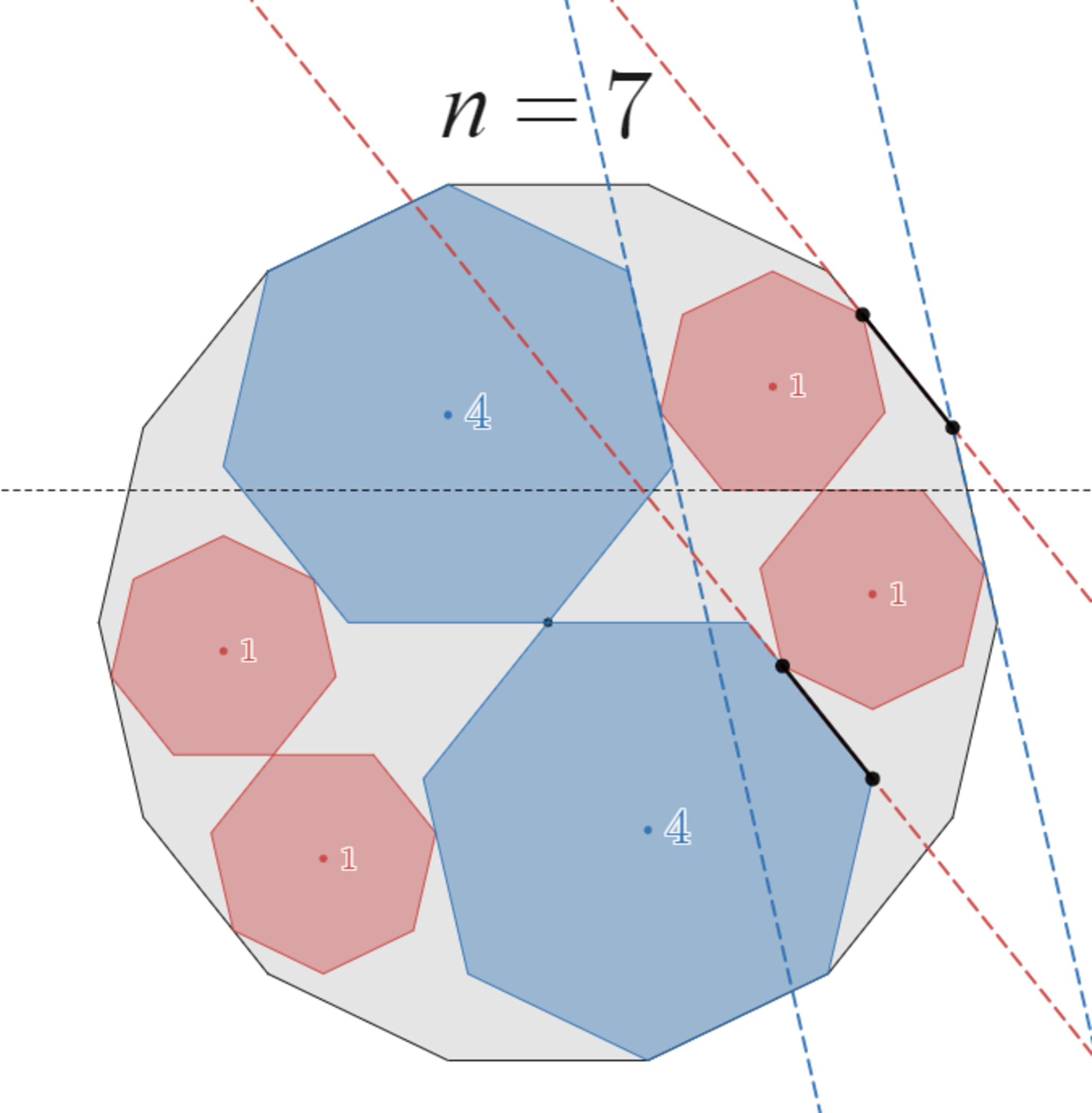 移動前の配置
移動前の配置
「移動前の配置」が可能であることは既に前回の記事で証明済みです。
赤線についての証明
まずは、赤線どおしは同じタイミングで角度が変わり、常に平行になっていることを示しましょう。
前回の記事の「系」と同様の考え方により、図の黒い線分は長さが同じであることがわかります。
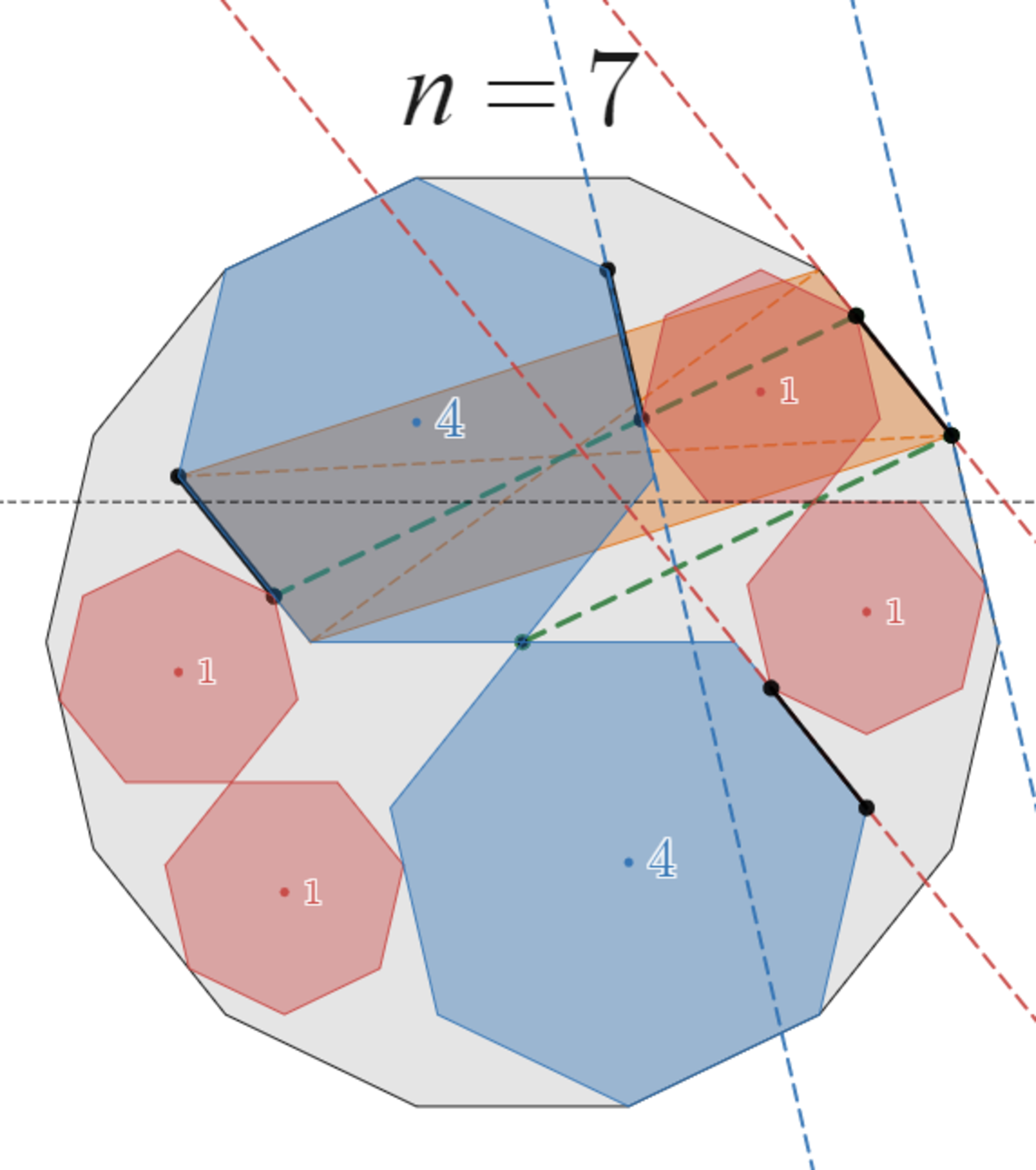 黒い線分の長さは全て同じになる
黒い線分の長さは全て同じになる
$C_1$ と $C_4$ の $y$ 座標の変位はこの移動中は常に同じ ですから、下図の黒い線は常に同じ長さになります。したがって、黒線の長さが $0$ になった次の瞬間から赤線の向きが同時に変わることがわかります。
![!FORMULA[149][36151][0] つめの頂点までの移動](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220814192634.gif?alt=media) $1$ つめの頂点までの移動
$1$ つめの頂点までの移動
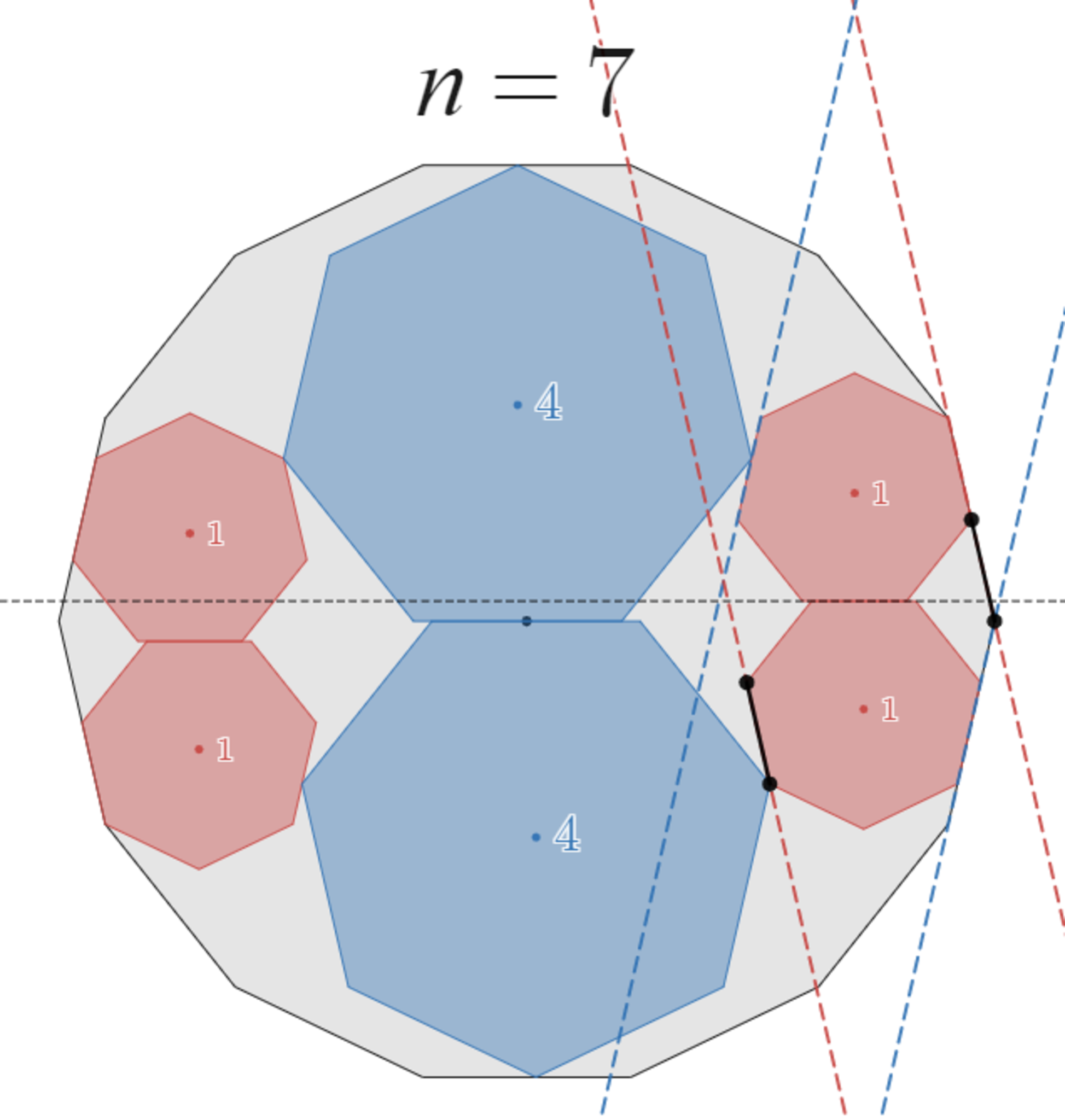 赤線の向きが変わった瞬間
赤線の向きが変わった瞬間
新しい赤線も平行になります。また、新たな黒線の長さは$C_1$の辺の長さと一致します。先ほどと同様に、この黒線の長さが $0$ になった次の瞬間から赤線の向きが同時に変わることがわかります。
![!FORMULA[152][36182][0] つめの頂点までの移動](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220814193355.gif?alt=media) $2$ つめの頂点までの移動
$2$ つめの頂点までの移動
次の新しい赤線も平行になります。また、新たな黒線の長さは$B_1$の辺の長さと一致します。ここから最後の配置まで、黒線の長さは常に一致します。
 最後の移動
最後の移動
というわけで、赤線は常に平行となります。
赤線についてのみ証明すればよい
では次に、青線も常に平行であることを示しましょう・・・と言いたいところですが・・・。
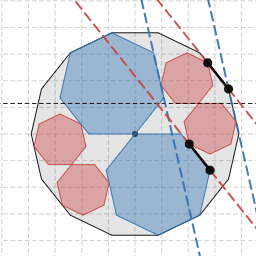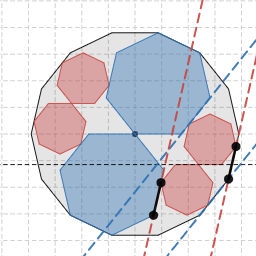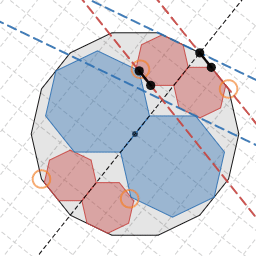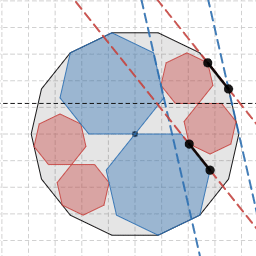 赤線と青線は鏡像の関係
赤線と青線は鏡像の関係
上図のとおり、図を直線 $y=\tan\dfrac{\pi}{n}$ に対して反転させると赤線と青線の位置は入れ替わりますから、青線についても赤線と同様、常に平行となります。
正"奇数"角形の場合の証明(辺接触の場合)
次に、移動前の配置で $C_1$が $A$ と「辺で接触する」場合について考えます。例えば、$n=11$ のときは辺で接触しています。
![正!FORMULA[158][1121120][0]角形の場合](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220814224539.png?alt=media) 正$11$角形の場合
正$11$角形の場合
辺接触かどうかわかりにくいので拡大してみました。確かに辺接触ですね。
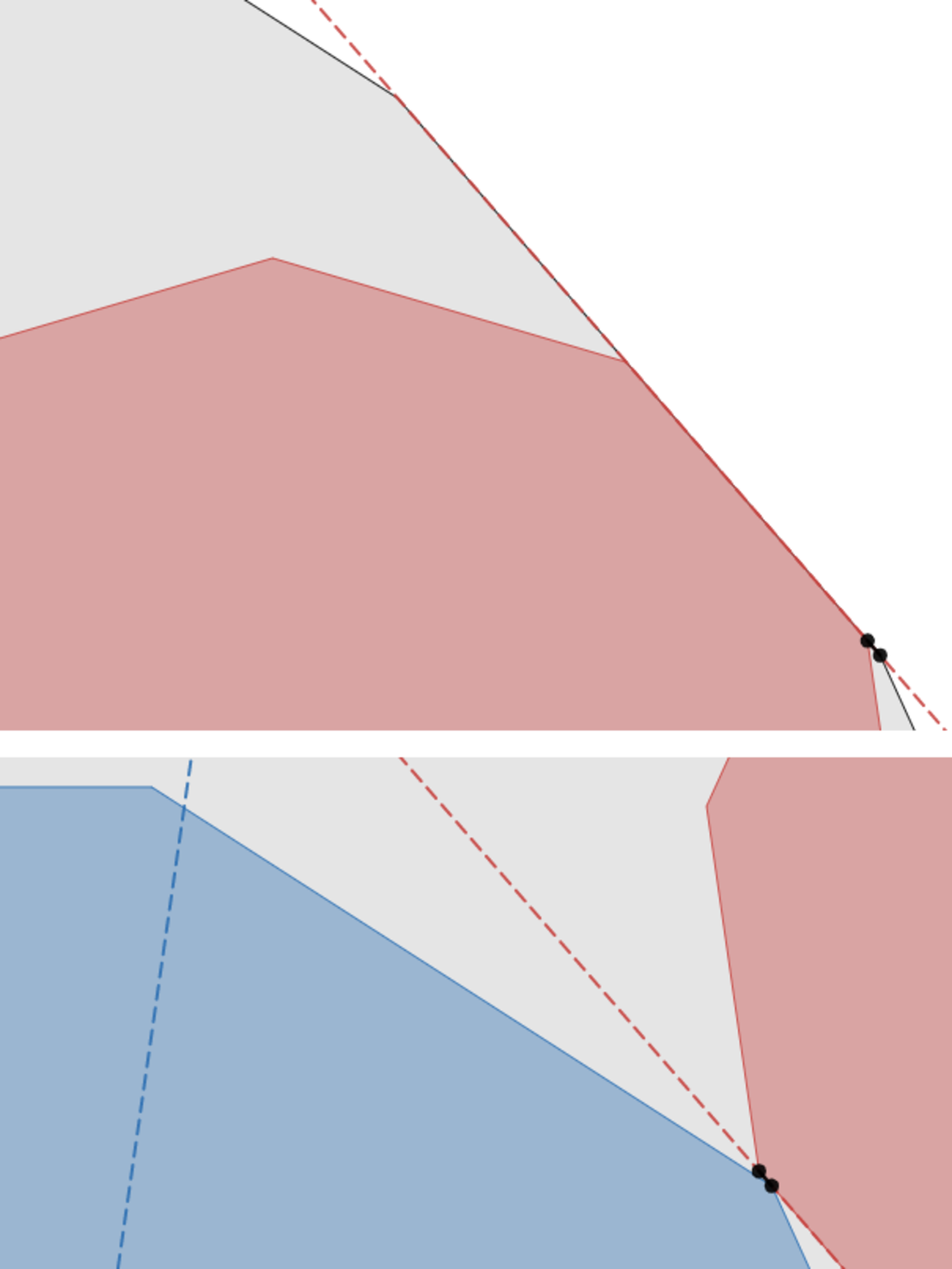 接触している部分の拡大図
接触している部分の拡大図
証明は、先ほどと全く同様に行うことができます。詳細は割愛しますが、下図を見ていただければご理解いただけると思います。
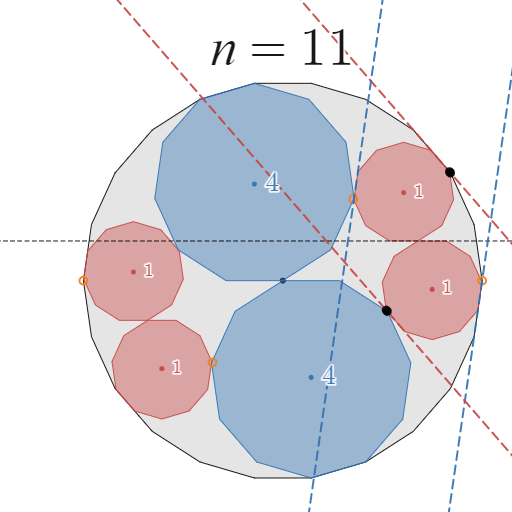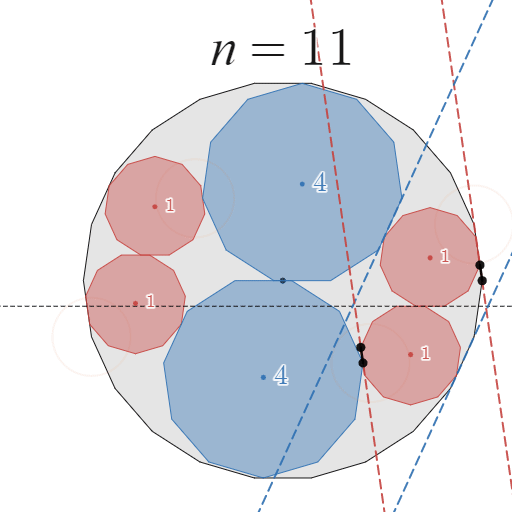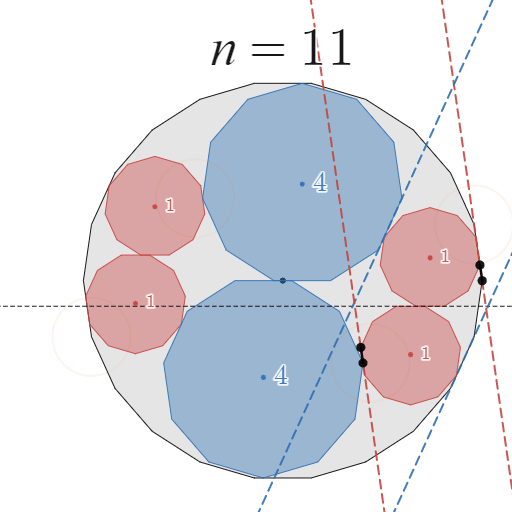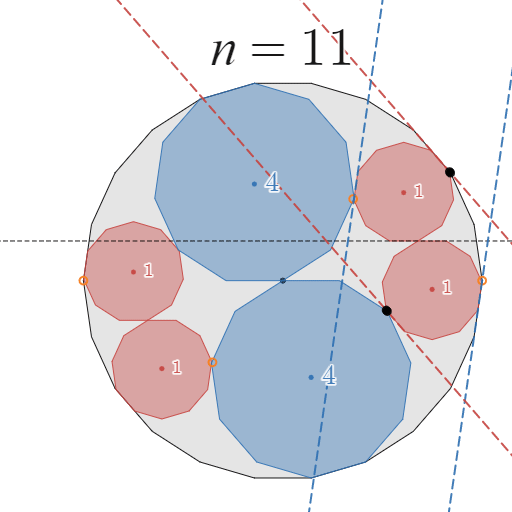 11
11
正"偶数"角形の場合の証明(概略)
同じ方法で偶数の場合も証明できます。
ここでは補助線の一例だけ紹介します。
方向転換したとき、次の頂点までの移動距離が必ず $C_1$ の一辺の長さの $3$ 倍になるところがポイントです。
![正 !FORMULA[161][1121089][0] 角形の場合の補助線の例](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220815193125.png?alt=media) 正 $10$ 角形の場合の補助線の例
正 $10$ 角形の場合の補助線の例
おわりに
直観的な証明ですませてしまい、厳密な証明の形にはなっていませんが、この問題に関しては厳密に表現するとかえって難解になってしまうと思います(言い訳)。
また、場合分けを全部まじめにやると膨大になってしまうので、途中からは端折ってしまいました。
とはいえ、どのパターンでも同様の方法で証明できるはずです。
Desmosファイルへのリンクを置いておきますので、いろいろ遊んでみてください。
この問題を考え始めた当初は「任意の $n$ について成り立つなんてあるわけないよね?」「任意の角度で同様の配置ができるなんてありえないよね?」と思っていましたが、最終的に、任意の正 $n$ 角形に対し、任意の角度で同様の配置が可能であることを発見することができました。
これほど美しい関係がこれまで知られていなかったというのは考えにくいような気もしますが、新発見でなかったとしても、このような美しい関係を発見することができたのは私にとって非常に感動的な出来事でした。ご協力いただいた皆さんにはあらためて感謝を伝えたいと思います。
記事の内容に関連する情報等ありましたらどんどん教えてくださいね。
今後ともよろしくお願いいたします。
