ISL2021N8

手数が多い問題は解いてて楽しいので解説を書いて楽しさを共有していきたいと思います. ($\#X$で集合の要素数を表します. 可能不可能とかは構成が可能か不可能かということです)

まず問題を見たら多項式をネストさせていることに目が行きます. すると2019JMO春P9とか次の補題とかを思い出します.

この補題を使う問題はたまにあるが( これとか , IMO2006P5とか , これ , これ )とりあえずは忘れて条件を満たす$n$を探してみよう. なんか取り得る値が$\bmod n$で大体半減する関数を見つければ良い.

$n=1$, 可能. それはそう.
$n=2$, $P(x)=2x, x(x+1)$とか. はい.
$n=3$, $P(x)=x^2+1$. はい. $\bmod p$で$x^2$の値域が$\dfrac{p-1}2$になるなーというお気持ちから思いつきそう.
$n=4$, $n=2$のアナロジーから$P(x)=2x, x(x+1)(x+2)$とか. 後者を先に思いつくと迷走しそう(自分は迷走した).
$n=5$...出来そうだし出来なさそう.
とりあえず$n=2^m$のときは$P(x)=2x$が回ってくれそうである. $n=3$が行けてるので$n=p$は可能そう. ここで$n=p$を考えてみる.

ここで何個かアイデアが浮かぶ. まず多項式に限らず一般の関数としてなら構成が存在しそうということ. 例えば$2$倍して良い感じに桁を切り捨てとか(多少やりにくそう), もっとやりやすいのは$2$で割って切り捨てであろう.
これは関数を有向グラフと見なすというイメージ化によっても認識しやすいと思う. なんか入次数$2$の頂点を沢山作ってあげれば良さそう.
また$\bmod p$の関数は全て多項式で表現出来る(これには気付かなくても構成出来るが). これは関数全体の集合の要素数が$p^p$個で因数定理を考えると$p-1$次以下の多項式は全て関数として異なるので$\bmod p$の多項式を関数としてみるとその個数は$p^p$個あるためである.
ということで構成が可能であることが分かったが実際に構成してみる. 上の考察にあるよう$2$で割って切り捨てる関数$f$を構成しよう. $n-2f(n)$は$0,1$しか取らず, $1$の部分はフェル小とかで強引に作れそう. この辺から$P(x)=\dfrac{p+1}2(n-(n(n-2)(n-4)\cdots(n-p+1))^{p-1})$が構成出来ると思う.

ということで$n$が$2$冪か素数のときは可能であることが分かった. 次は$n$が素冪でない場合を考えたい. というのも奇素数の冪で書ける数は$2$冪が可能なのを考えても構成が可能そうだし, かといって今までの構成が回るわけでは無く, この問題で一番ややこしい部分になりそうであるため, また素冪で無いものがどうなるかによって方針が大きく変わるためである.(あとは素冪でないとき中国の剰余定理が使えそうというのもある)

素冪でない正整数の最大の特徴と言えば互いに素な$2$以上の整数の積の形で書けることだろう. ということで, $n=ab$($a,b$は互いに素な$2$以上の整数)と書けると仮定する.
中国の剰余定理から$P^m(k)\bmod n$は$P^m(i)\bmod a$と$P^m(j)\bmod b$の組として考える事が出来る. ここで何かヤバいことが起こらないかと考えると(流石に不可能であることを予想している)$\left\lceil\dfrac n{2^m}\right\rceil=2$となる辺りでなんかおかしいことになりそうである. $\#P^m(\mathbb Z/a\mathbb Z)\cdot\#P^m(\mathbb Z/b\mathbb Z)=2$だから$\#P^m(\mathbb Z/a\mathbb Z),\#P^m(\mathbb Z/b\mathbb Z)$のどちらかが$1$になる. 対称性より$\#P^m(\mathbb Z/a\mathbb Z)=1$とする. するとある$t< m$があって$\#P^t(\mathbb Z/a\mathbb Z)\geq2, \#P^{t+1}(\mathbb Z/a\mathbb Z)=1$が成立する. すると$t,t+1$の前後で関数の$\bmod a$のとりうる値が半減してしまうので$\bmod b$のとりうる値は変化しない. よってこれ以降$\bmod b$でとりうる値の個数は変化しない!!!これは矛盾である.
これを理解するのには関数のネストの値域のイメージとして($X$を集合, $f:X\to X$とすると)$X\supset f(X)\supset f^2(X)\supset f^3(X)...$が成立することを持っておくと良いと思う. (これを使う問題はすぐには思い出せないけど無くはなかった気がする. A分野の集合と写像が出てくる問題にありそう)

ということで$n$が素冪の時が残った. これが可能か不可能か.
実はこれは不可能である. 自分は$n=9$の場合をプログラミングで全探索して確信を持った.(ずるい) まあ直感として構成するのは厳しそうという風にはなると思う. 例えば$\bmod p^2$の関数は$p^{2p^2}$個あるが多項式で表現出来る関数は$p^{2p(p-1)}$個より全然少ないのでそれに対して条件が厳しすぎるなという気分になるでしょう.

とりあえず状況設定を, $n=p^t$($p$は奇素数, $t$は$2$以上の整数)とします. $\mod p^t$での多項式の特徴といえば$\bmod p^s$($s< t$)で同じものの値は$\bmod p^s$で同じであるというものがあるでしょう. これは$P$に対する大きな制約となっていそうです. もう少し踏み込んで$k$の$\bmod p^s$の値を固定したとき$P(k)\bmod p^t$の取り得る値の個数はどのように評価出来るのかを考えたい. つまり何個かの値を確定したとき残りの値にどれくらいの制約が付くのかを精密化しようというノリである. で, これはヘンゼルの補題 (雑に言うと$\bmod p$での因数分解を帰納的に$\bmod p^N$に持ち上げるみたいな話) の考え方と酷似しているのでなんらかの議論ができそうである. $k\equiv a\pmod{p^s}$としたとき$k=a+bp^s$と書ける. そして$P(k)=P(a+bp^s)\equiv P(a)+bp^sP'(a)\pmod{p^{s+1}}$がわかる.(やっぱり微分便利(真面目にやると二項定理で示せる))だから$P'(a)\equiv 0\pmod p$ならとりうる値は$p^{t-s-1}$通り以下に, そうでないなら$p^{t-s}$通り全てが取れるみたいな感じになることが分かる. (このように帰納的に$p^N$に関する議論をすることは多いかも(すぐには例が出せないけど例えばJMOho2010P2とか OMC60Fとか? ISL1998N5とか? ))
結局$\bmod p^s$の値を固定すると取り得る値は(動ける値の個数と比べて)元と変わらないか$\dfrac1p$以下に減少する事が分かる.
前者後者どちらかになるかは$\bmod p$の値別に決まるので$s=1$の場合を考えるのが都合が良さそうである. $\bmod p$の類ごとに頂点を用意して$P$での値の行き先に辺を張った有向グラフを考えたい. ネストを繰り返し最後値が$1$通りになるのだからこのグラフはこんな感じ
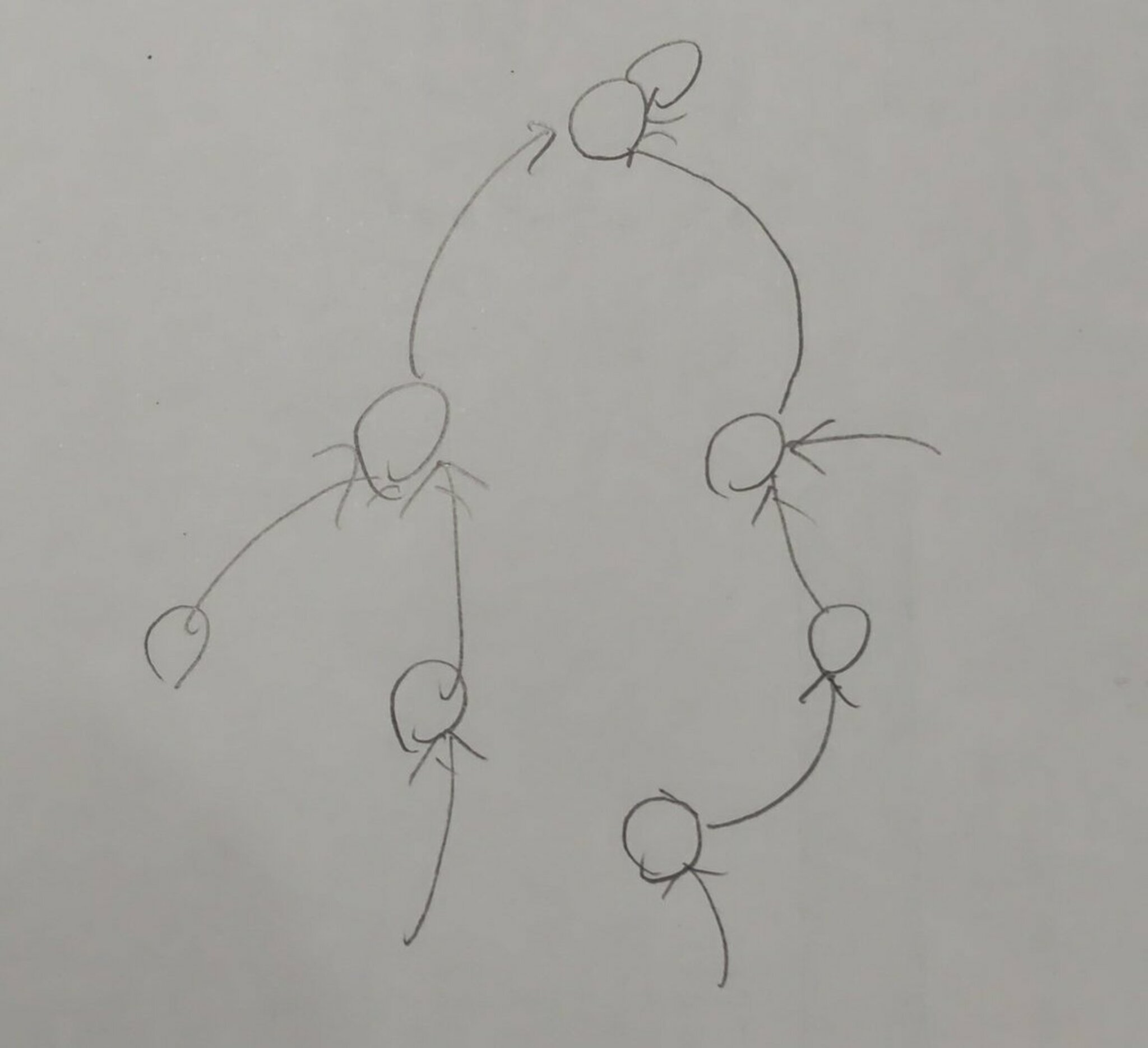木みたいなやつ
になるはず. これをみると不動点が丁度一個ある, これの類を$n\equiv \alpha\pmod p$とでも表すとこの類の$P^m$による$\bmod p^t$での行き先は$m$の増加に伴い常に$\dfrac1p$個以下に減っていく(最後$1$個になるまで).
だから全ての整数$k$に対して$P^m(k)\equiv \alpha\bmod p$が成立してしまえば後は$\dfrac1p$オーダーで取り得る値は減っていくし, $m\leq p$が成立するのだから$t$が十分大きいところでは$n=p^t$は不可能という結論を得る.($2< p$なので)

この議論の評価を改善していきたい. まず出来る事は取りうる値の個数が$\dfrac1p$になる場所をもっと精密に議論することだろう. というのも普通の状況を考えたら次の図のような感じで(黒い頂点に対応する類に$P$を作用させると取りうる値の個数が$\dfrac1p$になる)
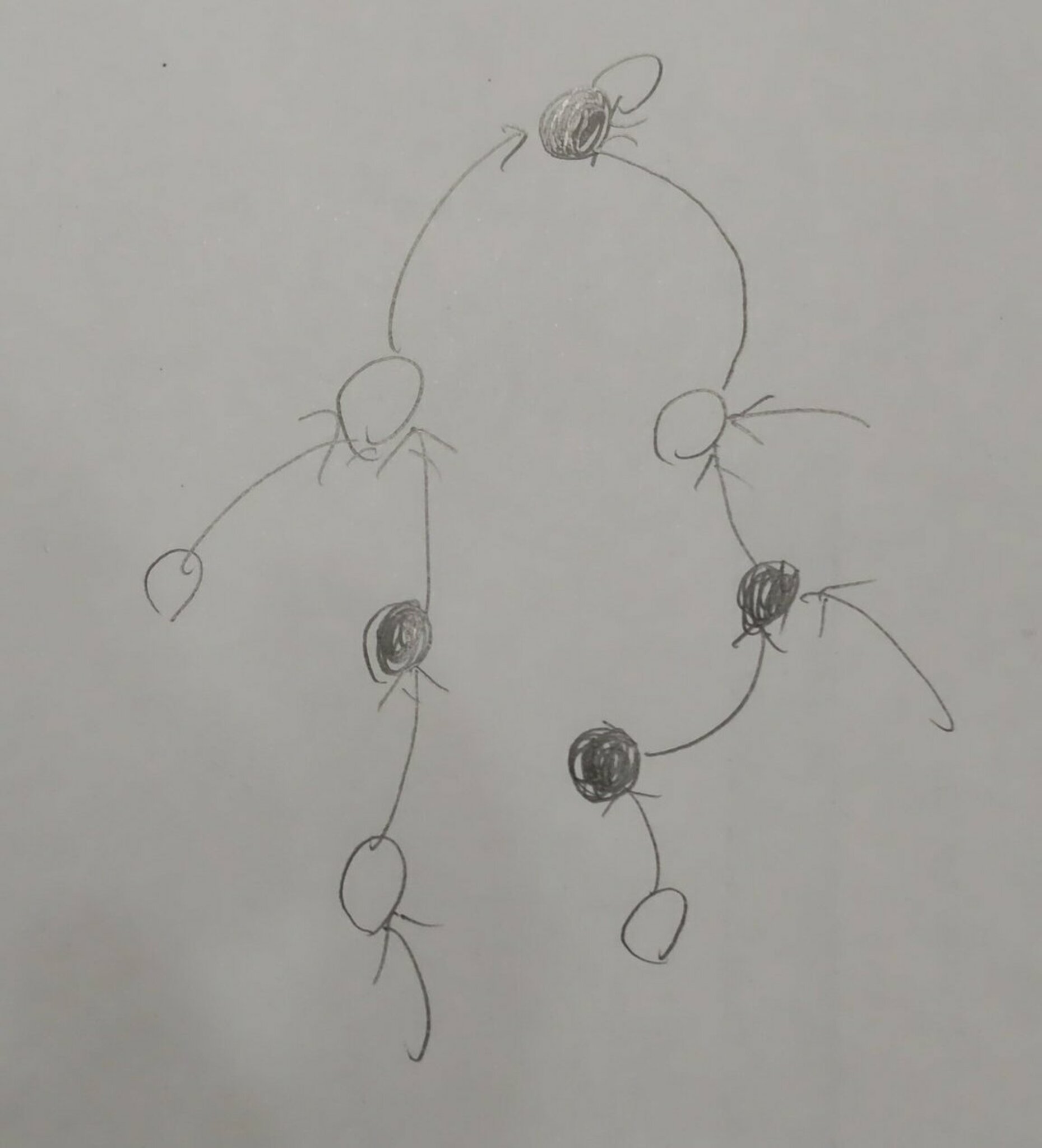イメージ
しかし極端なケースが問題である
極端なケース
左のケースなら早い段階($\log$オーダー)で一点に潰れるのでそれを使えば良さそう. 右のケースならもっと黒の頂点があるはず. するとわかることとして結構早い段階($\log$か定数ぐらいのオーダーで)で全部の類は(矢印を辿ると)黒頂点を通過するということである. そうすると全て黒頂点を通過した後取りうる値の個数は雑に評価しても$p^{t-1}$個なので$\left\lceil\dfrac {p^t}{2^m}\right\rceil$と良い勝負が出来そう.

というわけで全ての類が黒頂点を通過した時を$m$として, 最後に通過した類の一つを$k\equiv r\pmod p$として表そう. (これはISLにおける文字の置き方と同じなのでそちらも参照されたい) まず, $m$が$\log$オーダーで抑えられる事を言いたい. これは$a=\#P^{m-1}(\mathbb Z/p^t\mathbb Z)$から$b=\#P^m(\mathbb Z/p^t\mathbb Z)$に変わる際$r$の類のせいで$(p-1)p^{t-2}$以上要素数が減少するので, $a\leq2b, b\leq a$と合わせて評価出来そう. 実際には$P^{m-1}(\mathbb Z/p^t\mathbb Z)$から$r$の類の行き先を除いた集合の
$P$での行き先が$P^m(\mathbb Z/p^t\mathbb Z)$から$r$の類の行き先を除いたものを含むことを使って
$a\leq 2b=2(b-$($r$の類の行き先の要素数)$+p^{t-2})\leq 2(a-p^{t-1}+p^{t-2})$, 結局$2p^{t-2}(p-1)\leq a=\left\lceil\dfrac n{2^{m-1}}\right\rceil\leq 2b$が必要. だから$2^m$は大体$p$以下である事が必要なので$m$は$\log$オーダーで抑えられた.

$m$が$\log$オーダー($p$未満)で抑えられるということは上にあったグラフの行き先がまだ一点になっていない可能性が十分にあるのでそれを使った議論が出来そう. また, 二個上の段落の末尾の議論が回りそう(まだギリギリ厳しいか)という気分にもなるからそこら辺を精密に評価してみる. よって$\#P^m(\mathbb Z/p^t\mathbb Z)$の評価をする.

$m-1$回目の段階で$m$個の類は一点に集まっているのでそれらの像は高々$p^{t-2}$個. 残りの$p-m$個の類も黒い頂点を少なくとも一回通るのでその元の要素は高々$(p-m)p^{t-2}$個. 従って$b=\#P^m(\mathbb Z/p^t\mathbb Z)\leq (p-m+1)p^{t-2}$. あれ, 普通に上で見つけた$a,b$の評価と組み合わせたら評価回るじゃん.
$p^{t-2}(p-1)\leq(p-m+1)p^{t-2}$, つまり$m\leq2$.(?!!!!)
これはもうやるだけですね. $m\leq2$より$\dfrac{p^t}4\leq b\leq p^{t-2}(p-1)$.これより$p=2$.よって矛盾.

これにより求める$n$の条件は$n$は$2$冪または素数のとき.

勝利！

難しかった...手数多い...

グラフのイメージや帰納的に$p^n$を考えたり, いろんな事を駆使しましたね. あと周期性補題結局使わなかった()