一般化ガンマ分布に従う確率変数の対数の期待値

次の密度関数 $f(x;a,b,k)$ を持つ確率分布を一般化ガンマ分布（generalized gamma distribution）という.

\begin{align} f(x; a, b, k) = \frac{(k/b^a) x^{a-1} \exp(-(x/b)^k)}{\Gamma(a/k)}, \quad x > 0. \end{align}

$(a, b, k)$ はすべて正の値を取るパラメータである.

$(a, b, k)$ の値をいくつか適当に選んでプロットしたものが図1である.

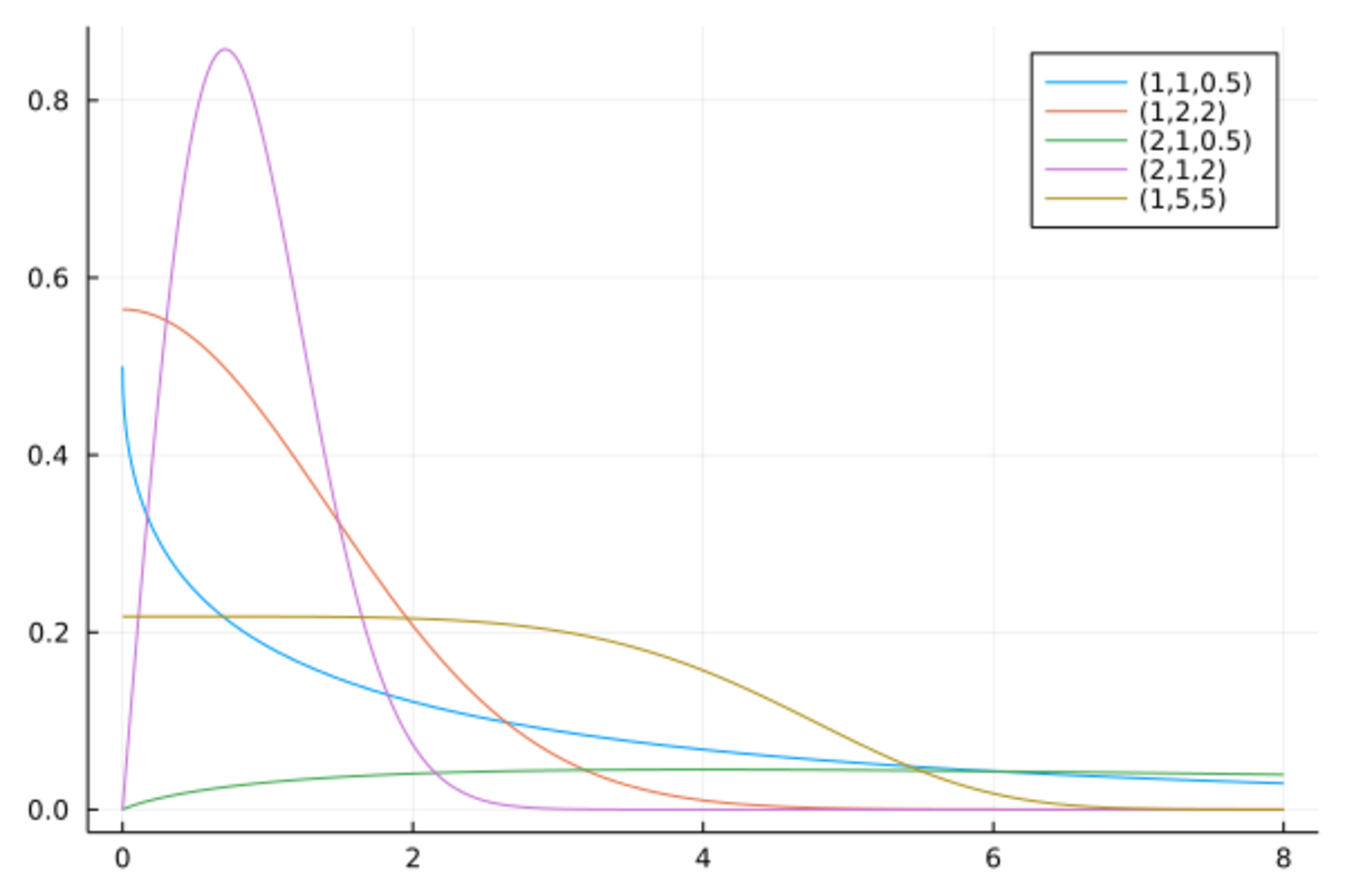一般化ガンマ分布の密度関数

確率変数 $X$ が一般化ガンマ分布に従うことを $X \sim \mathrm{GG}(a, b, k)$ と書くことにする.

いま, $X$ の自然対数をとった確率変数 $\log X$ の期待値 $E[\log X]$ を求めたい（そういうのを求めたい状況がたまにある）.

その準備として, ガンマ関数の定義を確認すると,

\begin{align} \Gamma(z) = \int^{\infty}_{0} t^{z-1}\exp(-t) \, dt \end{align}

である. $u = \log(t)$ と変数変換すると, $du = dt/t$より, ガンマ関数は,

\begin{align} \Gamma(z) = \int^{\infty}_{-\infty} \exp(uz-\exp(u)) \, du \end{align}

と書けることがわかる.

さて, 一般化ガンマ分布のパラメータ$b$はスケールパラメータで, $X \sim \mathrm{GG}(a, 1, k)$ のとき, $X$を$b$倍した$bX$は $\mathrm{GG}(a, b, k)$ に従う.

そこで, $X \sim \mathrm{GG}(a, 1, k)$ の場合を考える.

\begin{align} E[\log X] &= \int^{\infty}_{0} \log (x) \frac{k x^{a-1} \exp(-x^k)}{\Gamma(a/k)} \, dx \\ &= \frac{1}{\Gamma(a/k)} \int^{\infty}_{0} k\log (x) x^a \exp(-x^k)\, dx/x \end{align}

$y=k\log (x)$と置き, $dy/k=dx/x$より,

\begin{align} E[\log X] &= \frac{1}{\Gamma(a/k)} \int^{\infty}_{-\infty} y \exp((a/k)y-\exp(y))\, (dy/k)\\ &= \frac{1}{\Gamma(a/k)} \int^{\infty}_{-\infty} \frac{\partial}{\partial a} \exp((a/k)y-\exp(y))\, dy\\ &= \frac{1}{\Gamma(a/k)} \frac{\partial}{\partial a}\left( \int^{\infty}_{-\infty} \exp((a/k)y-\exp(y))\, dy\right)\\ &=\left(\frac{\partial}{\partial a}\Gamma(a/k)\right)\frac{1}{\Gamma(a/k)}\\ &=\psi(a/k)/k. \end{align}

ここで$\psi(z)$はディガンマ関数
$$ \psi(z) = \frac{d}{dz} \log \Gamma(z) $$
である.

$E[\log(bX)]=E[\log(X)]+\log(b)$ なので, $X \sim \mathrm{GG}(a, b, k)$ のときは $E[\log(X)]=\psi(a/k)/k+\log(b)$.

検算は Generalized gamma distribution in Julia (GitHub Gist) のように行った.

ちなみに, $X \sim \mathrm{GG}(a, 1, k)$ の場合の $E[X]$ を定義通り計算すると,

\begin{align} E[X] &= \int^{\infty}_{0} x \frac{k x^{a-1} \exp(-x^k)}{\Gamma(a/k)} \, dx \\ &= \frac{k}{\Gamma(a/k)} \int^{\infty}_{0} x^{a} \exp(-x^k)\, dx. \end{align}

ここで $y=x^k$ と置くと, $x=y^{1/k}$, $dx/dy = (1/k)y^{1/k-1}$ より, $x^{a}\,dx=(1/k)y^{(a+1)/k-1} \, dy$ なので,

\begin{align} E[X] = \frac{\Gamma((a+1)/k)}{\Gamma(a/k)} \end{align}

であるから, $X \sim \mathrm{GG}(a, b, k)$ のときは $E[X]=b\frac{\Gamma((a+1)/k)}{\Gamma(a/k)}$.