テトラキューブの敷き詰め(教員採用試験・算数)
はじめに
広島県の教員採用試験(小学校・算数)で次のような問題が出題されました.
※問題に誤りがあったため,現在は公開されていません.
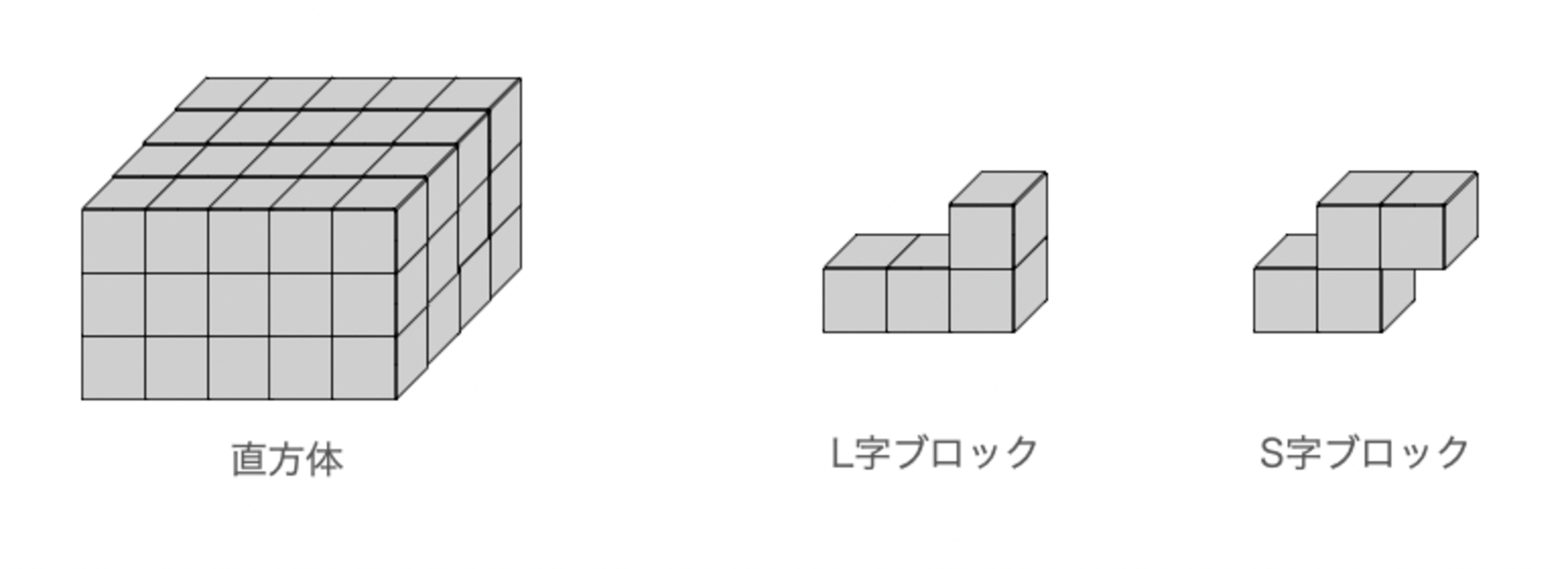
次のようなL字型ブロックとS字型ブロックを組み合わせて,$3\times 4 \times 5$の直方体をつくる.
- L字型ブロックをできるだけ多く使うとき,L字型ブロックとS字型ブロックのそれぞれの個数を求めよ.
- S字型ブロックをできるだけ多く使うとき,L字型ブロックとS字型ブロックのそれぞれの個数を求めよ.
ただし,1,2 いずれにおいても,1個も使用しないブロックがあってもよい.
L字ブロックをできるだけ多く使う場合
まず,直方体全体に含まれる小立方体の個数は$3\times 4 \times 5$で,L字ブロック,S字ブロックに含まれる小立方体の個数はともに4個なので,直方体を作るには,L字ブロックまたはS字ブロックを合計で$3\times 5= 15$個使う必要があります.
L字ブロックをできるだけ多く使う場合について考察すると,多少の試行錯誤により,L字ブロック15個を用いて(すなわち,S字ブロックは使用しない)直方体を完成させることができます.従って,1番の問題は解けました.
S字ブロックをできるだけ多く使う場合
こちらは少し難しいです.まず,こちらも試行錯誤により,S字ブロック13個,L字ブロック2個で直方体を完成させることができることがわかります(やってみてください).
そこで,次の問題を考えることにします.
(1) S字ブロック14個,L字ブロック1個の組み合わせで直方体を作ることができるか.
(2) S字ブロック15個で直方体を作ることができるか.
この(1),(2)を解くことができればこの問題は解決です.
(1) S字ブロック14個,L字ブロック1個の組み合わせ
試行錯誤により,直方体を作ることはできなさそうに感じたので,次のことを示します.
S字ブロック14個,L字ブロック1個の組み合わせでは$3\times 4 \times 5$の直方体を作ることはできない.
敷詰め問題の定番の手法を用います.$3\times 4\times 5$の直方体が$4\times5$の$3$段で構成されていると考えて,各段の小立方体に次のように番号を振ります.
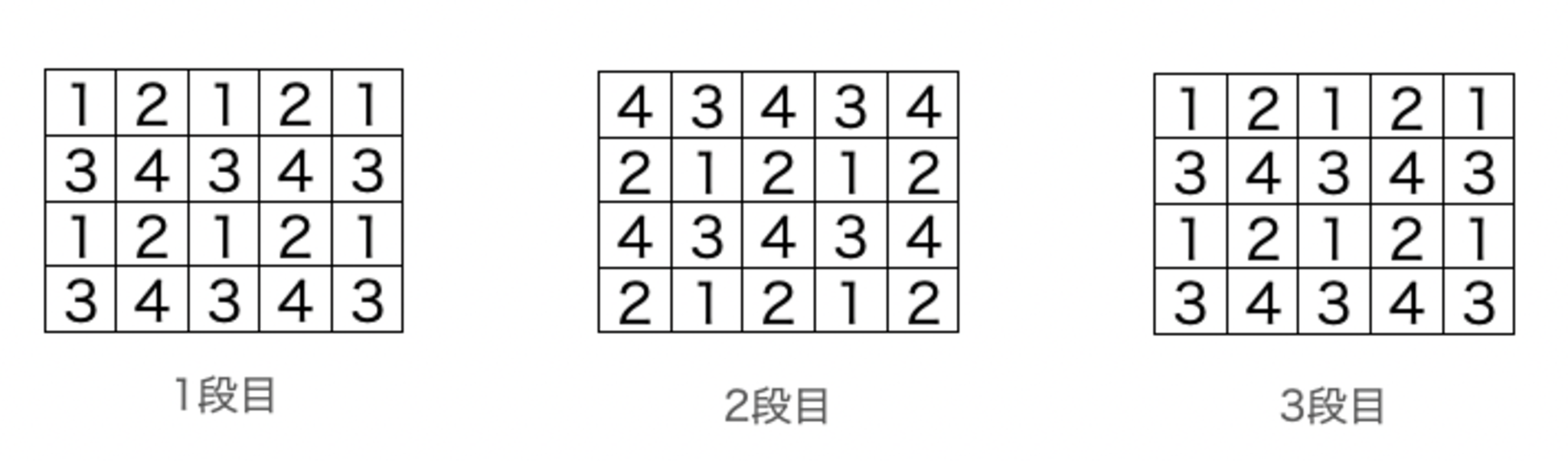
各小立方体に振った数字の個数を数えると,次のようになっている.
| 数字 | 個数 |
|---|---|
| 1 | 16 |
| 2 | 14 |
| 3 | 16 |
| 4 | 14 |
このように数字を振った直方体にS字ブロックを置くと,必ず次が成り立つ.
- S字ブロック1個で,1,2,3,4を必ず1個ずつ覆う.
また,L字ブロックを置くと必ず次が成り立つ.
- L字ブロック1個で,$a,a,b,c$と覆う.ただし,$a,b,c$は1〜4のいずれかで,互いに異なる.
したがって,S字ブロックを14個使った段階で,直方体に書かれている数字のうち,覆われていないものの個数を数えると次のようになっている.
| 数字 | 個数 |
|---|---|
| 1 | 2 |
| 2 | 0 |
| 3 | 2 |
| 4 | 0 |
この状態になった直方体をL字ブロックで覆うことはできないことが,先ほどの考察からわかる.
以上から,S字ブロック14個,L字ブロック1個の組み合わせでは,$3\times 4 \times 5$の直方体を作ることはできないことがわかった.
(2) S字ブロック15個
さきほどと同様の方針で次のことを示します.
S字ブロック15個では$3\times 4 \times 5$の直方体を作ることはできない.
直方体に振る数字のパターンを変えて次のようにします.

それぞれの数字の個数は
| 数字 | 個数 |
|---|---|
| 1 | 18 |
| 2 | 12 |
| 3 | 18 |
| 4 | 12 |
である.
S字ブロックを置いたときの数字を覆うパターンは次のいずれか.
- 1,2,3,4を1個ずつ覆う.
- 1,1,3,3と覆う
- 2,2,4,4と覆う
(i),(ii),(iii)のような置き方をするS字ブロックの個数をそれぞれ$x,y,z$として,立方体の個数と各数字の個数に注目すると,$x,y,z$は次の連立方程式を満たす必要があることがわかります.
$$
\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z = 15 \\
x+2y = 18 \\
x+2z = 12
\end{array}
\right.
\end{eqnarray}
$$
この連立方程式の解は$(x,y,z) = (0,9,6)$です.したがって,もしS字ブロック15個で直方体を作ることができる場合は,(ii)のような置き方をするブロック9個と(iii)のような置き方をするブロック6個の組み合わせしかあり得ないということです.
そのような置き方では直方体を作ることができないことは次のことからわかります.さきほど数字を振った直方体を,さらに次のように色分けします.

(ii)または(iii)の置き方は,どちらも色をまたがないような置き方になっています(それぞれのブロックは青のみ,または白のみを覆う).したがって,直方体を作るためには$4 \times 3$の長方形をS字ブロック4個でぴったり覆う必要があるがそれは不可能です.
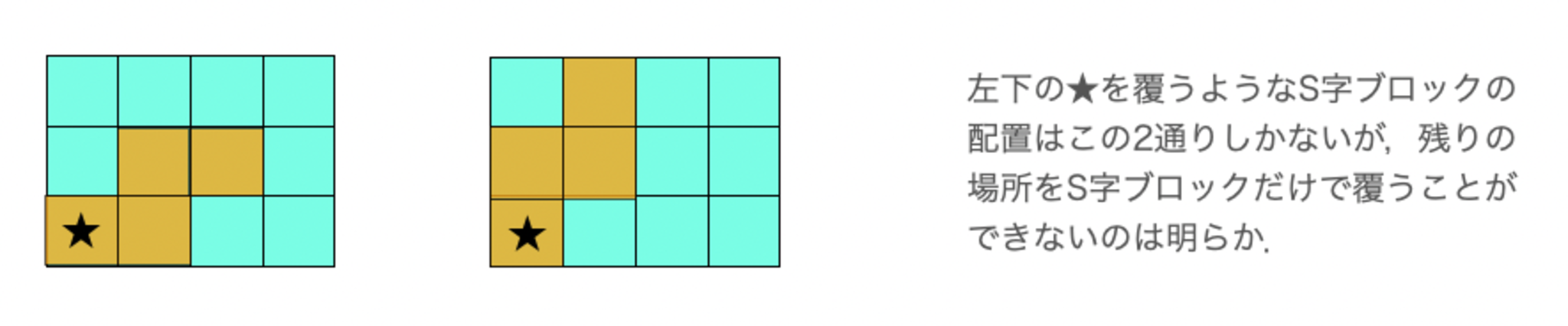
以上から,S字ブロック15個でも直方体を作ることができないことがわかった.
おわりに
なかなか難しい問題だったように思います.議論の不備や誤り等あればご指摘ください.
このような敷詰め問題は,敷き詰めることができるための必要条件を考えて,それを満たさないから敷詰めできない,というような問題が多い印象です.敷詰めできるための十分条件についてはかなり難しいのでしょうか?どなたかご存知の方がいらっしゃいましたら是非教えてください.
また,この問題を考えるにあたって色々調べたのですが,平面上の敷詰めについては記事や文献が多少あったのですが,空間における敷詰めはあまり情報がありませんでした.そちらについてもお教えいただけるとありがたいです.
