極線と極の性質+Metachickの自作問題の解説

579

はじめに

先日,twitterにて自作問題を投稿させていただきました.解いてくださった方は本当にありがとうございました!!今回はそちらの解答・解説を載せたいと思います.また,解説の補足として極と極線の解説もしていますのでよかったら見ていってください!

解答

分野:A/★☆☆☆☆

正実数 $a, b, c$ は $a + b + c = a b c$ を満たす.このとき,以下の不等式を示せ.
$\frac{{(a b c)}^{2}}{(a^{2} + 1) (b^{2} + 1) (c^{2} + 1)} \leq \frac{27}{64}$

典型を組み合わせた問題でした.普通に斉次式化を考えてゴリゴリやっていっても解けないことはないでしょうが,計算地獄に陥ると思うので工夫しましょう.
・ $a + b + c = a b c$ という条件を見たらtanによる置換を考える
・ $\tan^{2} X + 1 = \frac{1}{\cos^{2} X}$ 等の関係式を用いて整理する.
・AM-GMやJensen等の有名不等式を用いる.

$\tan A = a, \tan B = b, \tan C = c$ となるように $A, B, C$ を定める.ただし, $0 \leq A, B, C < 2 π$ である.この時,条件より, $\tan A + \tan B + \tan C = \tan A \tan B \tan C$ であるから, $A + B + C = π$ となる.

$\begin{aligned} \frac{{(\tan A \tan B \tan C)}^{2}}{(\tan^{2} A + 1) (\tan^{2} B + 1) (\tan^{2} C + 1)} & = {(\sin A \sin B \sin C)}^{2} \\ \leq {(\frac{\sin A + \sin B + \sin C}{3})}^{6} ∵ (A M - G M) \\ \leq {(\frac{3 \sin (\frac{A + B + C}{3})}{3})}^{6} ∵ (J e n s e n) \\ = \sin^{6} \frac{π}{3} \\ = \frac{27}{64} \end{aligned}$

不等号の等号成立条件は全て一致しているため題意は示された.

分野:N/★★☆☆☆

$n, k$ を $2$ 以上の正整数とする. $n^{k!} - 1$ は $k$ 未満の任意の素数 $p$ に対して $p$ で割って $1$ 余る $1$ でない約数を持つことを示せ.

難しい議論かと思いきや,ただの因数分解でした.それ故に逆に沼にハマってしまった人もいるのではないでしょうか.

$\begin{aligned} n^{k!} - 1 & = (n - 1) (n^{k! - 1} + n^{k! - 2} + \dots + n^{2} + n + 1) \end{aligned}$
である.ここで $p$ を $k$ 未満の素数とすると, $(n^{k! - 1} + n^{k! - 2} + \dots + n^{2} + n + 1)$ は $S = (n^{p} + n^{p - 1} + \dots + n^{2} + n^{1} + 1)$ , $S^{'} = (n^{p - 1} + n^{p - 2} + \dots + n^{2} + n^{1} + 1)$ を約数に持つ.ここで, $n \equiv 1 (m o d p)$ の時 $S \equiv 1 (m o d p)$ であり, $n ≢ 1 (m o d p)$ の時 $S^{'} = \frac{n^{p} - 1}{n - 1} \equiv \frac{n - 1}{n - 1} = 1 (m o d p)$ となる.これらは明らかに $1$ ではないので題意は示された.

(約数に持つことは因数分解を考えればわかります.これは項を $i$ 個ずつまとめる方法での因数分解を考えれば良いですね.)

続いては,階乗進法を用いた奇抜な変形で解く方法を紹介します!

$\begin{aligned} n^{k!} - 1 & = (n - 1) (n^{k! - 1} + n^{k! - 2} + \dots + n^{2} + n + 1) \\ = (n - 1) (n^{1!} + 1) (n^{2 \cdot 2!} + n^{2!} + 1) \dots (n^{(k - 1) (k - 1)!} + n^{(k - 2) (k - 1)!} + \dots + n^{2 (k - 1)!} + n^{(k - 1)!} + 1) \end{aligned}$
ただし,最後の変形に関しては階乗進法の一意性を用いた.

$n^{p!} - 1$ の約数 $S = n^{p \cdot p!} + n^{(p - 1) p!} + \dots + n^{2 \cdot p!} + n^{p!} + 1$ を考える.このとき,フェルマーの小定理より $n$ が $p$ の倍数でないならば $n^{p!} \equiv 1 (m o d p)$ であるから, $S \equiv 1 (m o d p)$ が従う. $n$ が $p$ の倍数であるなら明らかに $S \equiv 1 (m o d p)$ である.よって題意は示された.

分野:G/★★★★★

円 $Ω$ に内接する六角形 $A B C D E F$ は $| A B | = | B C |, | C D | = | D E |, | E F | = | F A |$ を満たす. $Ω$ の $A, B, C, D, E, F$ における接線をそれぞれ $L_{A}, L_{B}, L_{C}, L_{D}, L_{E}, L_{F}$ とする. $L_{A}$ と $L_{C}$ の交点を $B^{'}$ , $L_{B}$ と $L_{D}$ の交点を $C^{'}$ , $L_{C}$ と $L_{E}$ の交点を $D^{'}$ , $L_{D}$ と $L_{F}$ の交点を $E^{'}$ , $L_{E}$ と $L_{A}$ の交点を $F^{'}$ , $L_{F}$ と $L_{B}$ の交点を $A^{'}$ とするとき, $A^{'} D^{'}, B^{'} E^{'}, C^{'} F^{'}$ は一点で交わることを示せ.

この問題はさまざまなエレガントな回答が送られてきました！ここでは,それらを中心に紹介していきたいと思います.とまぁ,その前にまずは努力で誰にでも道が開ける複素座標での回答を載せておきましょう.

図を描くとこんな感じになります.
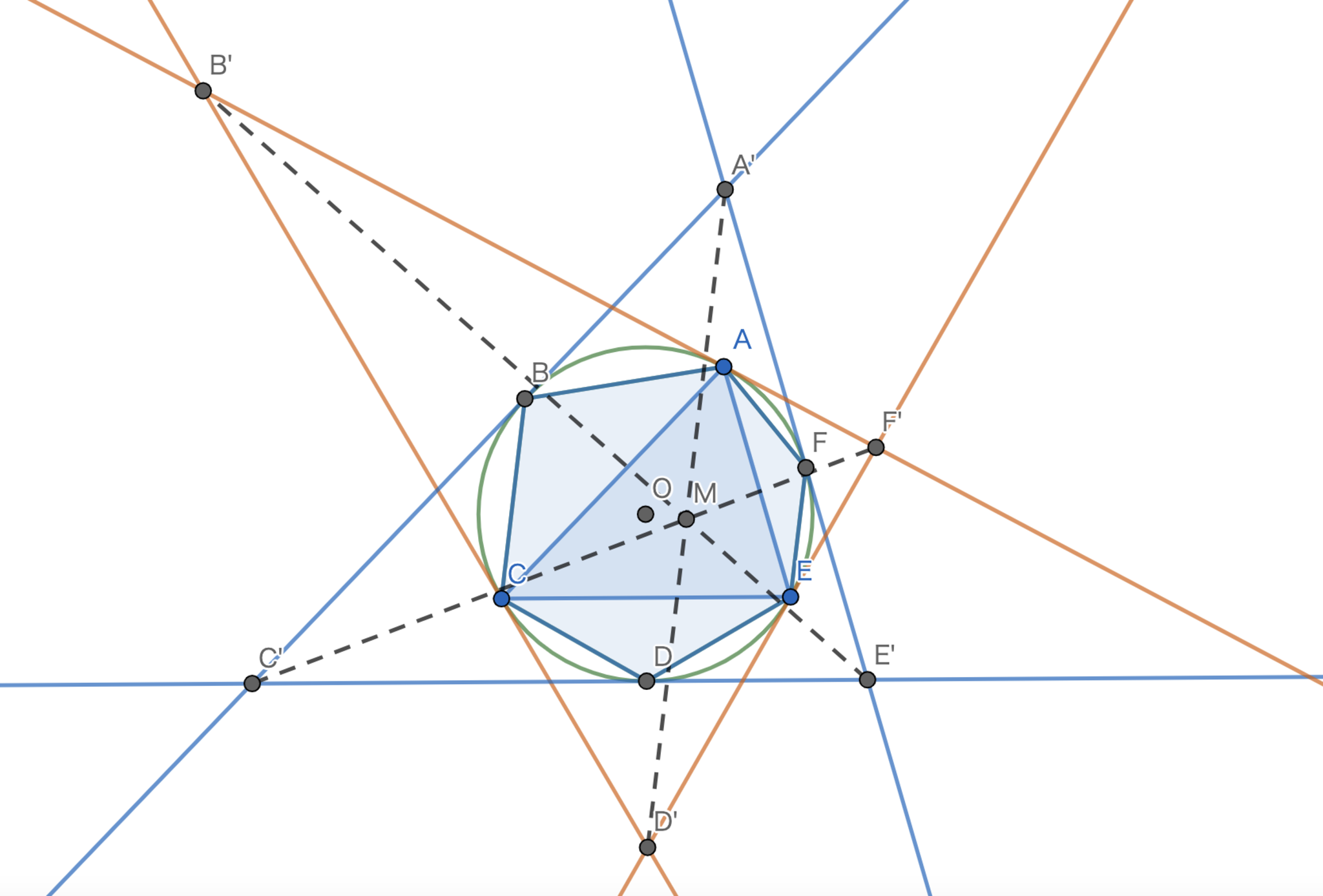第三問-図

複素座標

方針:うまく三点 $A, C, E$ の座標を定めて使う文字数を減らす.(一度は初等的に考えてみましょう.すると,角の二等分線が登場することに気付けると思います.そこで,うまく座標設定ができることを思いつくでしょう.)
$A (a^{2}) B (- a c) C (c^{2}) D (- c e) E (e^{2}) F (- e a)$
となるようにうまく座標を定める.このとき
$A^{'} (- \frac{2 a c e}{c + e}) B^{'} (\frac{2 a^{2} c^{2}}{a^{2} + c^{2}}) C^{'} (- \frac{2 a c e}{e + a}) D^{'} (\frac{2 c^{2} e^{2}}{c^{2} + e^{2}}) E^{'} (- \frac{2 a c e}{a + c}) F^{'} (\frac{2 e^{2} a^{2}}{e^{2} + a^{2}})$
が得られる. $A^{'} D^{'}$ の式を考えていく.このとき, $\bar{A^{'}} (- \frac{2}{a (c + e)}), \bar{D^{'}} (\frac{2}{c^{2} + e^{2}})$ であることに留意して,
$A^{'} D^{'} : (\bar{A^{'}} - \bar{D^{'}}) z - (A^{'} - D^{'}) \bar{z} = \bar{A^{'}} D^{'} - A \bar{D^{'}} ⟺ - \frac{2 c^{2} + 2 e^{2} + 2 a c + 2 a e}{a (c + e) (c^{2} + e^{2})} z + \frac{2 c e (a c^{2} + a e^{2} + c^{2} e + c e^{2})}{(c + e) (c^{2} + e^{2})} \overset{―}{z} = - \frac{4 c^{2} e^{2}}{a (c + e) (c^{2} + e^{2})} + \frac{4 a c e}{(c + e) (c^{2} + e^{2})} ⟺ - (a c + a e + c^{2} + e^{2}) z + a c e (a c^{2} + a e^{2} + c^{2} e + c e^{2}) \overset{―}{z} = 2 a^{2} c e - 2 c^{2} e^{2}$
となる.ここで, $z = - (a c + c e + e a)$ を代入する.(内心)
$(a c + a e + c^{2} + e^{2}) (a c + c e + e a) - a c e (a c^{2} + a e^{2} + c^{2} e + c e^{2}) (\frac{1}{a c} + \frac{1}{c e} + \frac{1}{c a}) = 2 a^{2} c e - 2 c^{2} e^{2}$
が成り立つので $A^{'} D^{'}$ は内心を通る.このとき,対称性より $B^{'} E^{'}, C^{'} F^{'}$ も内心を通るので三直線は一点,特に内心で交わることが示された.

さて,ここからは初等的な証明方法です！まずはBrianchonの定理を用いたエレガントな解法です.こちらは翁さんからいただきました!Brianchonの定理ってこうやって使うんだぁ〜という感じです.

Brianchonの定理/@I_______nu

$A D, B E, C F$ は内心 $I$ で交わる. $L_{B}, L_{C}, L_{E}, L_{F}$ で囲まれた四角形を六角形が退化したものと考えてBrianchonの定理を適用する.この時, $A^{'} D^{'}, B E, C F$ は共点であり,特に内心 $I$ で交わる.従って, $A^{'} D^{'}$ は $I$ を通る.同様にして, $B^{'} E^{'}, C^{'} F^{'}$ も $I$ を通るから題意は示された.

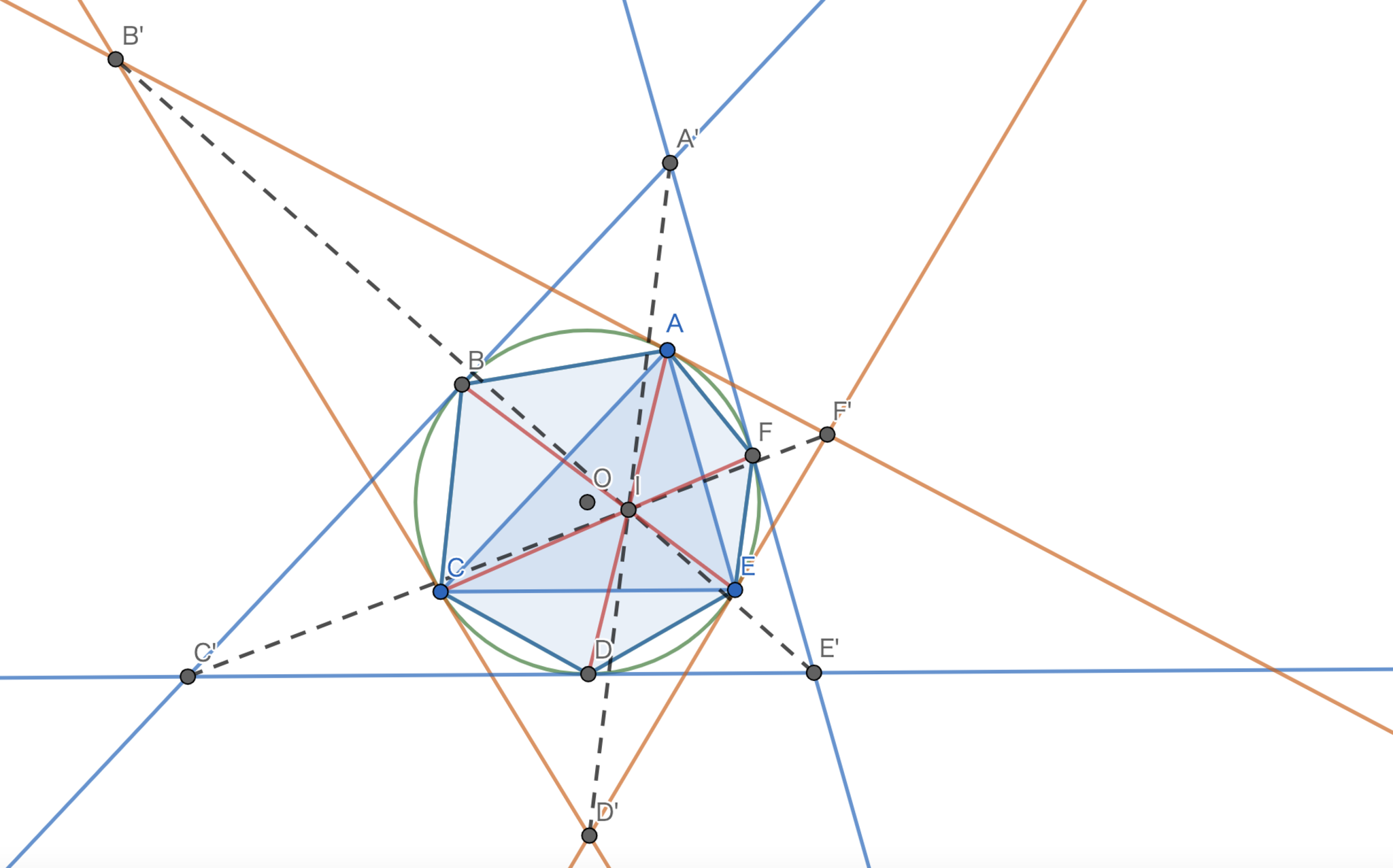第三問-brianchonの定理

次は極線と極の性質を用いた解法です.解説の下に極線と極の性質について,軽くまとめましたのであまり詳しくない方は先にご覧になってください.こちらは HighSpeedさんからいただきました!とてもエレガントです.

極の性質/@mktexlsr

図のように点 $P, Q, R, S, T, U$ を定める.

この時, $∠ A B D = ∠ P B A$ であり, $| A B | = | B C |$ より $∠ A D B = ∠ C A B = ∠ P A B$ であるから, $△ A D B ∽ △ P B A$ となる.よって, $| A P | = \frac{| B D |}{| A B | \cdot | A D |}$ となる.同様に, $| A S | = \frac{| A F |}{| D F | \cdot | A D |}$ , $| C R | = \frac{| D F |}{| C D | \cdot | C F |}$ , $| C U | = \frac{| B F |}{| C B | \cdot | C F |}$ , $| E Q | = \frac{| B D |}{| E B | \cdot | E D |}$ , $| E T | = \frac{| B F |}{| E B | \cdot | E F |}$ となる.

$∠ A T U = ∠ A F T + ∠ T A F = ∠ A F B + ∠ E A F = ∠ B A C + ∠ F B A = ∠ B A A + ∠ U B A = ∠ A U T$ となるので, $| A T | = | T U |$ である.同様に, $| C P | = | C Q |, | E R | = | E S |$ が得られる.

ここで,図のように $X, Y, Z$ を定める.ここで,Menelausの定理と上記で得たことを併せて, $\frac{| E X |}{| X C |} = \frac{| E B | \cdot | E F |}{| C B | \cdot | C F |}$ である.同様に, $\frac{| C Y |}{| Y A |} = \frac{| C D | \cdot | C F |}{| A D | \cdot | A F |}$ , $\frac{| A Z |}{| Z E |} = \frac{| A B | \cdot | A D |}{| E B | \cdot | E D |}$ である.

これと $| A B | = | B C |$ 等を併せて以下を得る.

$\frac{| E X |}{| X C |} \cdot \frac{| C Y |}{| Y A |} \cdot \frac{| A Z |}{| Z E |} = \frac{| E B | \cdot | E F |}{| C B | \cdot | C F |} \cdot \frac{| C D | \cdot | C F |}{| A D | \cdot | A F |} \cdot \frac{| A B | \cdot | A D |}{| E B | \cdot | E D |} = \frac{| A B |}{| B C |} \cdot \frac{| C D |}{| D E |} \cdot \frac{| E F |}{| F A |} = 1$ .従って,Menelausの定理より, $X, Y, Z$ は共線である. $B F, C D$ は $A^{'}, D^{'}$ を極とした極線であるから,極 $X$ の極線は $A^{'} D^{'}$ である.同様に極 $Y, Z$ の極線は $B^{'} E^{'}, C^{'} F^{'}$ である. $X, Y, Z$ は共線なので, $A^{'} D^{'}, B^{'} E^{'}, C^{'} F^{'}$ はいずれも直線 $X Y Z$ の極を通る.従って,題意は示された.

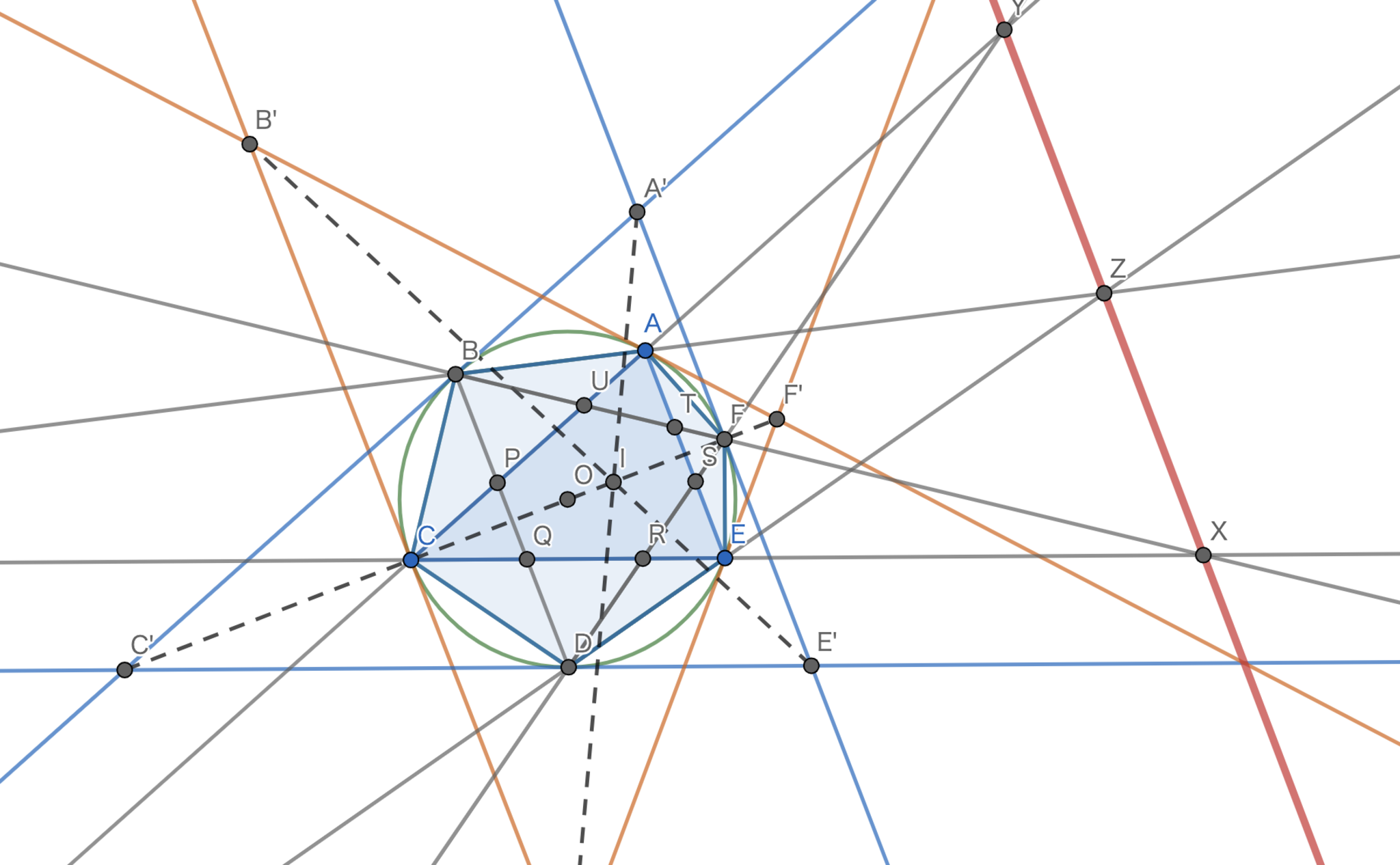第三問-極の性質

極の性質を用いた回答でした.次に紹介するのは,最初から双対をとってしまうという方法です.本質的には上の解答と同じですから,どちらの解法を選ぶかは好みです.こちらはまいんさんにいただいた解答です.スタイリッシュです.

双対命題/@I_my_mine_math

双対命題を考える.この時, $X, Y, Z$ を図のように定める. $\frac{| X E |}{| C X |} \cdot \frac{| Y A |}{| E Y |} \cdot \frac{| Z C |}{| A Z |} = (\frac{| E F |}{| B C |})^{2} \cdot (\frac{| A B |}{| D E |})^{2} \cdot (\frac{| C D |}{| F A |})^{2} = 1$ であるから,Menelausの定理より題意は示された.

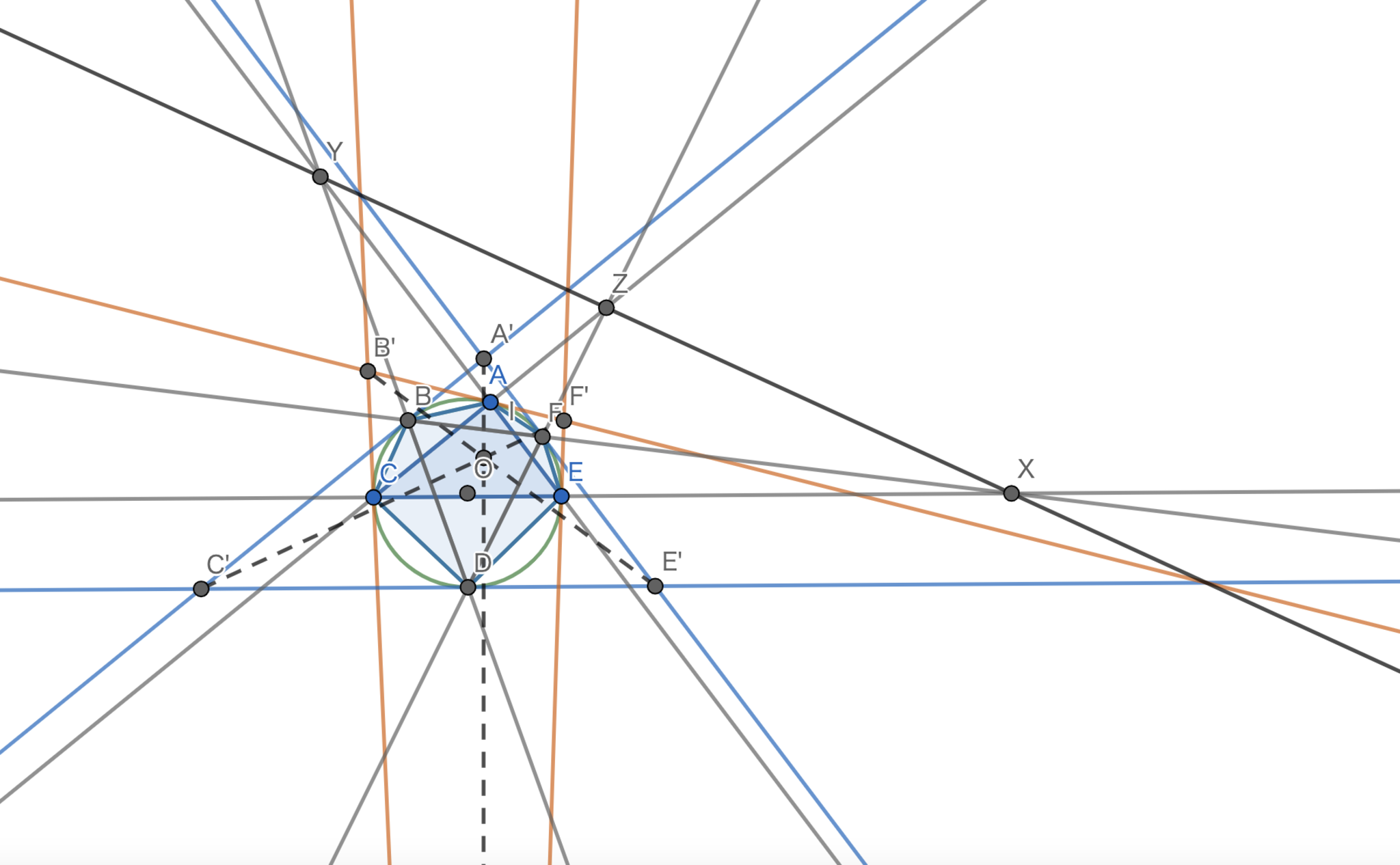第三問-双対命題

極線と極の性質

極と極線-極が円外の場合

$O$ を中心とする円に対して,点 $P$ をとる. $P$ から円に引いた二つの接線の接点を結んだ直線を極線という.この時の $P$ を極(極点)という.

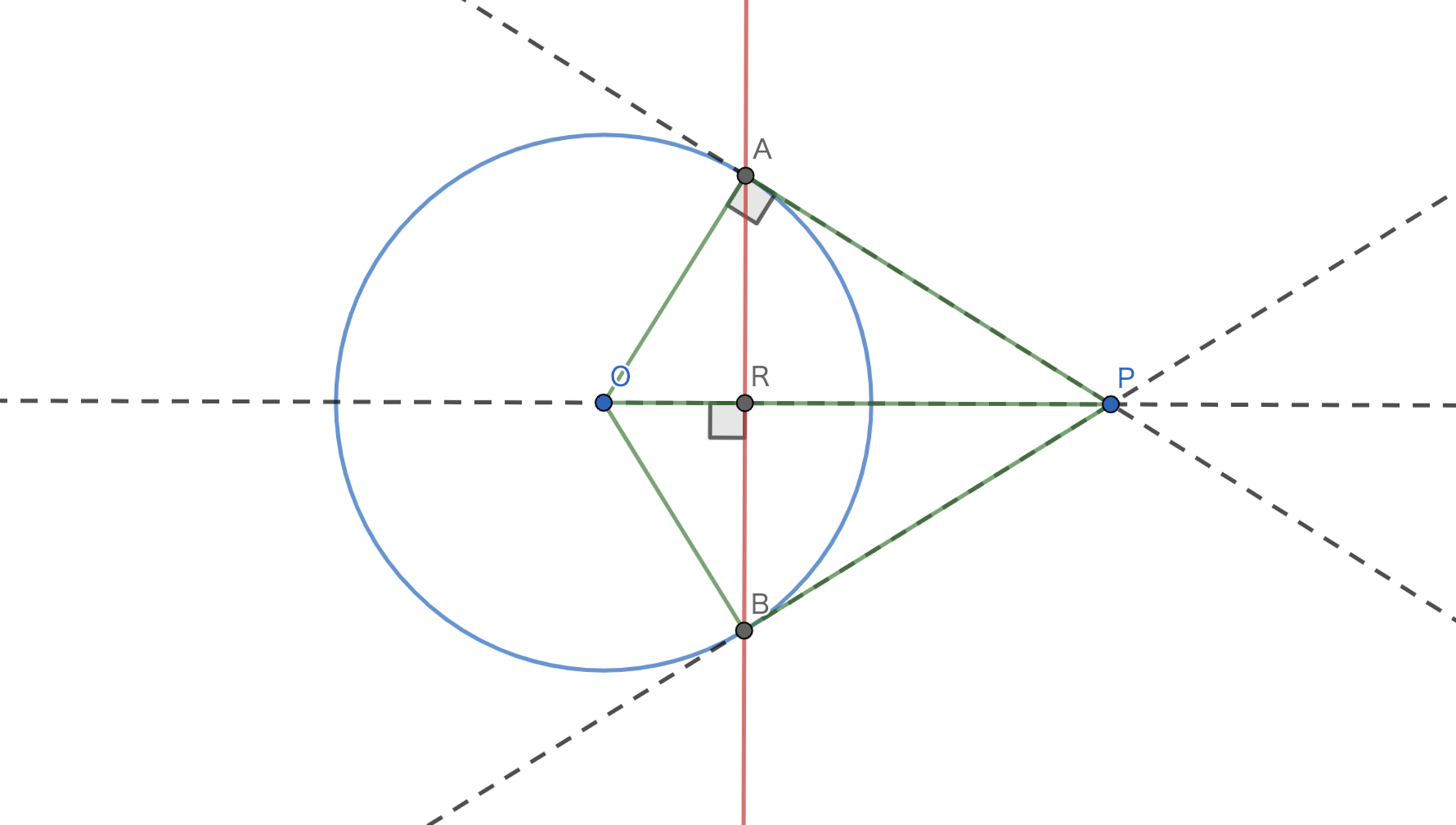極と曲線-極が円外の場合

極と極線-極が円内の場合

$O$ を中心とする円に対して,点 $P$ をとる. $O P$ の $P$ における垂線と円の交点のうち一つを $R$ とする.円の $R$ における接線と $O P$ の交点を $Q$ とする.この時, $Q$ を通り, $O P$ に垂直な直線を極線という.この時の $P$ を極(極点)という.

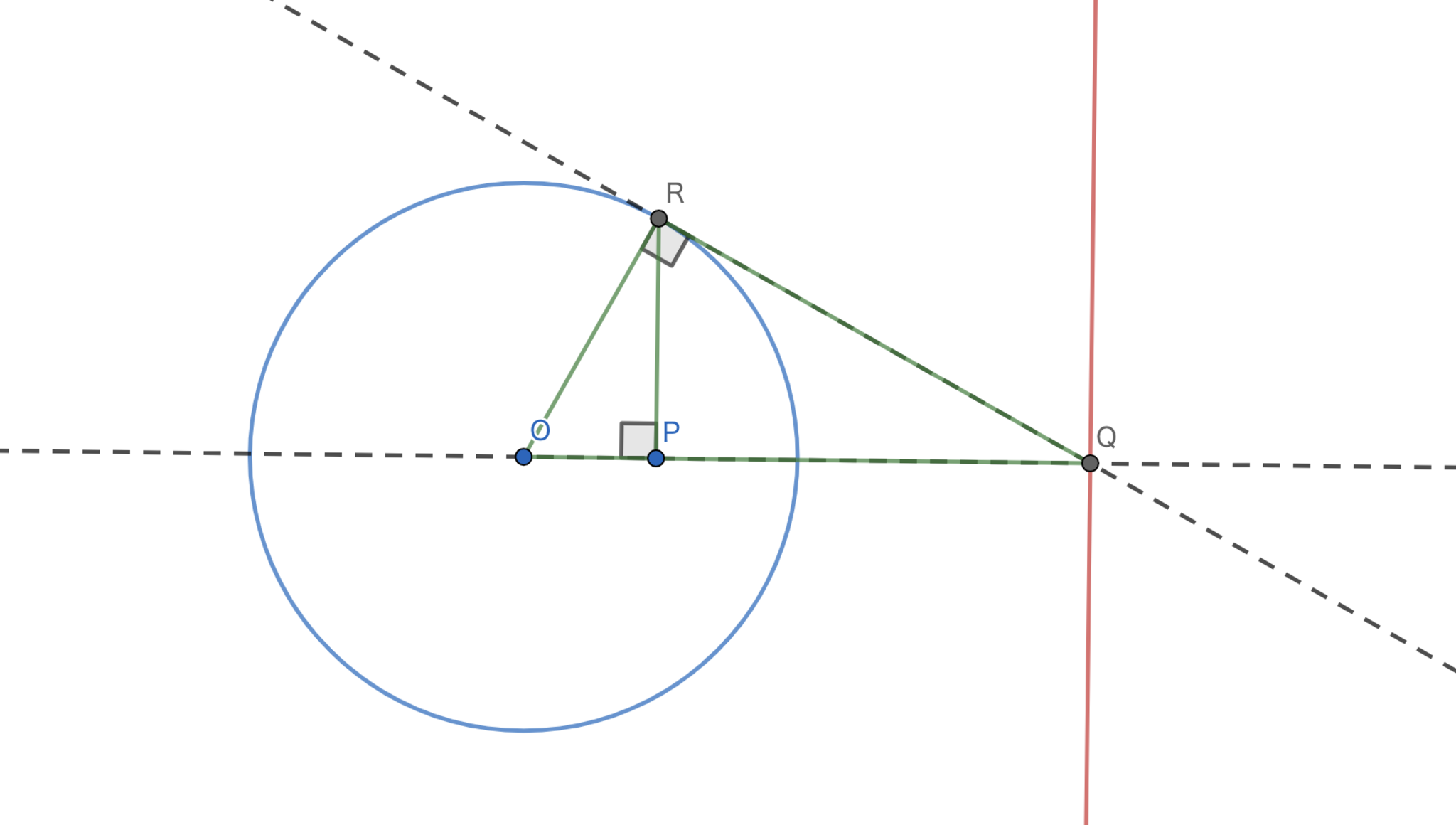極と極線-定義1

極と極線は二次曲線に対して定義できるものですが,今回は初等的に扱うことができる円に限定して話を進めていきます.また,定義の表現を直感的にするために一部変更しています.

極線と調和点列

図において, $(P, Y; X, Z) = 1$ である.

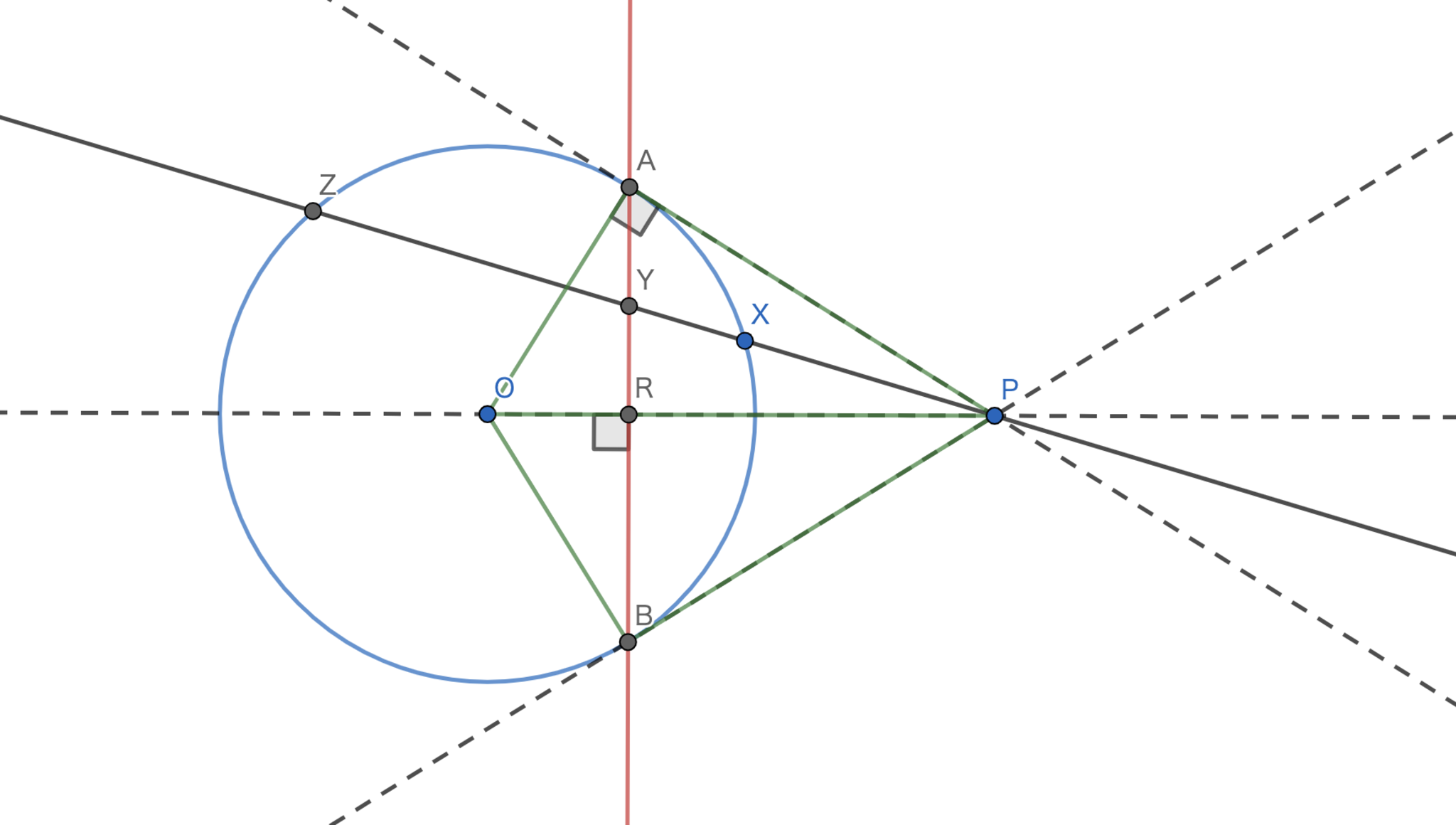極線と調和点列

点 $X$ の取り方は円周上であれば自由です.

二つの極線

$O$ を中心とする円に対する極を $P, P^{'}$ として,極線を $L, L^{'}$ とする.この時, $P$ が $L^{'}$ 上に存在するならば $P^{'}$ は $L$ 上に存在する.

$∠ P Q^{'} P^{'} = 90 °$ を示せば良い. $| O P | \cdot | O Q | = | O R |^{2}$ , $| O P^{'} | \cdot | O Q^{'} | = | O A |^{2} = | O R |^{2}$ となるので,四点 $P, Q^{'}, P^{'}, Q$ は共円である. $A B ⊥ O P^{'}$ であり, $∠ P Q P^{'} = 90 °$ である.ここで, $P, Q^{'}, P^{'}, Q$ は共円であるから $∠ P Q^{'} P^{'} = 90 °$ が得られる.従って,題意は示された.

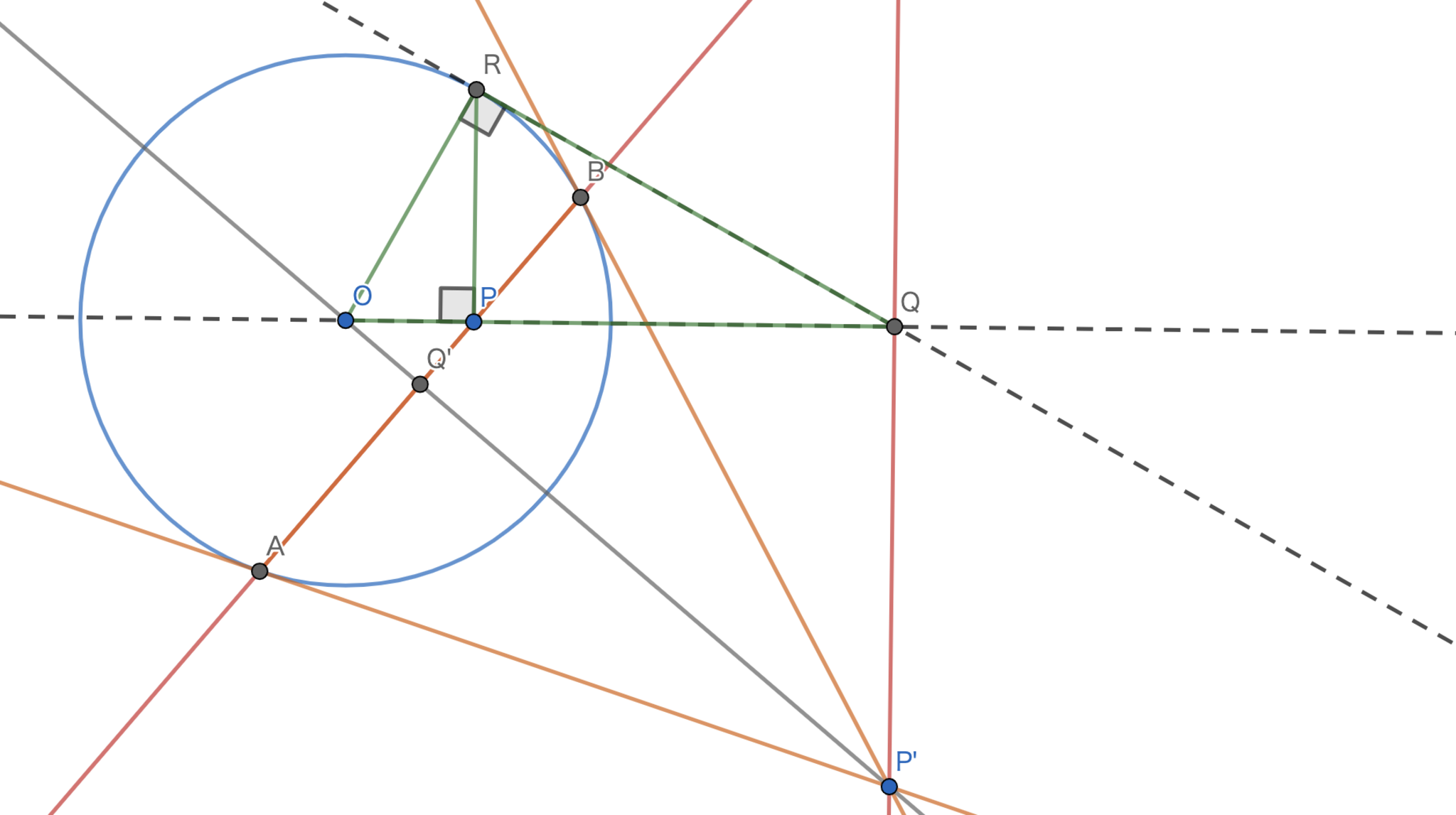二つの極線

さて,この定理から何が得られるでしょうか...?直線が点の集合であったことを思い出してみましょう. $P, P^{'}$ を極. $L, L^{'}$ を極線として, $P, P^{'}$ がそれぞれ $L^{'}, L$ 上であるという状況を考えます. $P, L$ を固定して $P^{'}$ を動かすことを考えてみましょう.すると, $L^{'}$ は一点 $P$ を常に通り続けることが定理2よりわかります.従って,極と極線は一対一に対応しているとみることができる訳です.これを双対の原理と言います.これをまとめると以下のようになります.

極線の双対

直線 $L$ 上の点 $P^{'}$ を極とする極線は $L$ の極 $P$ を常に通る.
点 $P$ を通る直線 $L^{'}$ の極 $P^{'}$ は $P$ の極線 $L$ 上の点である.

定理2より明らか.

さて,せっかくなので極と極線の性質を使う定理を見てみましょう.

Brocardの定理

円に内接する四角形 $A B C D$ において, $A C, B D$ の交点を $O^{'}$ ,外接円の中心を $O$ とする.直線 $A B$ と直線 $C D$ 交点を $P$ ,直線 $B C$ と直線 $D A$ の交点を $Q$ とするとき, $P O^{'} ⊥ Q O, P O ⊥ Q O^{'}$ である.

方針:完全四辺形に隠れている調和点列を発見する

$P R$ と $Q A$ の交点を $X$ , $Q R$ と $P A$ の交点を $Y$ とする.この時, $(Q, X; A, D) = 1, (P, Y; A, B) = 1$ であるから, $X O^{'}, Y O^{'}$ はそれぞれ $Q, P$ を極とする極線である.それらはどちらも $O^{'}$ を通ることから $O^{'}$ は $P Q$ を極線とするとその極である.極線の定義より, $O O^{'} ⊥ P Q$ である. $P O^{'}$ と $Q O$ の交点を $R$ , $O O^{'}$ と $P Q$ の交点を $E$ ,円の半径を $r$ とする.この時, $| O R | \cdot | O Q | = r^{2}$ であり, $| O O^{'} | \cdot | O E | = r^{2}$ であるから,四点 $Q, R, O^{'}, E$ は共円である. $∠ Q E O^{'} = 90 °$ より, $∠ O^{'} R Q = 90 °$ となる.