“領域”の通過領域（GeoGebra?!）

165

この記事の目標

この記事は，数学Ⅱ（及び体系数学4）の「図形と方程式」で頻繁に出題される〈直線の通過領域〉を更に発展させて，〈領域と通過領域〉についての問題を紹介することで，この手の問題をさらに理解しよう！という目標です。一部，数Ⅲの知識を要します。

また，GeoGebraとMathlogを組み合わせられるかの実験も兼ねています。

問題

座標平面において，$\mathrm{O}(0,\,0)$を中心とする半径$1$の円$C$があり，その内部に点$\mathrm{A}(a,\,0)\;(0\lt a\lt 1)$ を取る。$C$上の $2$点$\mathrm{P}$，$\mathrm{Q}$が$\kaku{PAQ}=90^{\circ}$を満たしながら動くとき，以下の問に答えなさい。

⑴　$\beku{a}=\bekutoru{OA}$，$\beku{p}=\bekutoru{OP}$，$\beku{q}=\bekutoru{OQ}$とおくとき，$\beku{p}\mdot\beku{q}-\beku{a}\mdot(\beku{p}+\beku{q})$ の値を$a$を用いて表しなさい。
　
⑵　線分$\mathrm{OA}$の中点を$\mathrm{M}$とする。線分 $\mathrm{PQ}$の中点$\mathrm{R}$は，$\mathrm{P}$，$\mathrm{Q}$の位置によらず$\mathrm{M}$を中心とするある定円上にあることを示し，その円の半径を$a$を用いて表しなさい。
　
⑶　⑵の円の内部の領域（境界線上は除く）を$D$とし，$C$上に定点$\mathrm{A_0}(1,\,0)$をとる。$\mathrm{A}$が線分$\mathrm{OA_0}$上（両端は除く）を動くとき，$D$が通過する範囲の面積を求めなさい。

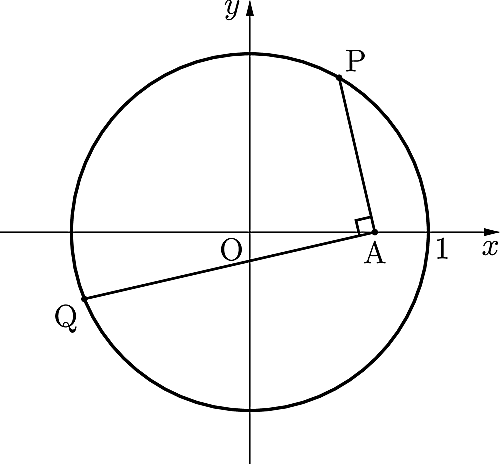問題の状況（一例）

問題の状況を画像としてみました。（$\rm\TeX$の背景を透過処理しているため，なにかしらの不具合があるかもしれません。その場合はコメントしていただけると助かります！）

以下解答を与えます。まず先に手を動かして考えてみることを推奨します。なにも考えないで答えを見ると，相当効率が落ちると思うので。。。
目標解答時間は$25$分ぐらいかなあと。

考え方やお気持ちなどを述べながら解答を書いていきます。

⑴の解答

やはり$\kaku{PAQ}=90^{\circ}$が与えられているので，〈内積は$0$〉を利用するのが一般的と思います。逆にそれ以外の答案があったら教えてほしいです。

$\kaku{PAQ}=90^{\circ}$より，$(\beku p-\beku a)\mdot(\beku q-\beku a)=0$である。これを変形すれば，$$ \beku p\mdot \beku q-\beku a\mdot(\beku p+\beku q)+|\beku a|^2=0 $$
である。$|\beku a|=a$だったので，$\beku p\mdot \beku q-\beku a\mdot(\beku p+\beku q)=\pmb{-a^2}$

⑵の解答

せっかくベクトルで考えるように誘導がありますので，問題文をベクトルで言い換えることを試みます。すると，$|\bekutoru{MR}|$が一定であることを示せばよいことに気づきます。

$|\bekutoru{MR}|$が一定であることを示せばよい。$$ \bekutoru{OM}=\bunsuu{\beku a}{2},\qquad \bekutoru{OR}=\bunsuu{\beku p+\beku q}{2} $$であるので，
$$ \begin{align} |\bekutoru{MR}|^2&=|\bekutoru{OR}-\bekutoru{OM}|^2\\ &=\bunsuu{(\beku p+\beku q)^2-2(\beku p+\beku q)\mdot\beku a+|\beku a|^2}{4}\\ &=\bunsuu{|\beku p|^2+|\beku q|^2+|\beku a|^2+2\Big(\beku p\mdot \beku q-\beku a\mdot(\beku p+\beku q)\Big)}{4} \end{align} $$ここで，$|\beku p|=|\beku q|=1$，$|\beku a|=a$ および⑴の結果を代入することで，
$$ \begin{align} |\bekutoru{MR}|^2 &=\bunsuu{1+1+a^2-2a^2}{4}\\ &=\bunsuu{2-a^2}{4} \end{align} $$
$0< a< 1$より，$\quad |\bekutoru{MR}|=\bunsuu{\tsqrt{2-a^2}}{2}=\text{（一定）}$
よって，点$\mathrm R$は，$\mathrm M$を中心とする半径$\bunsuu{\sqrt{2-a^2}}{2}$の円周上にある。

⑶の解答

ここまでは普通のベクトルの問題なので，それほど難しくはなかったはずです。⑶が本番です。

とりあえず，問題の状況をGeoGebraに描画しました。URLをクリックした先では，$a$の半径と$\rm P$をマウスで動かすことが出来ます。
https://www.geogebra.org/m/dqdzer2g

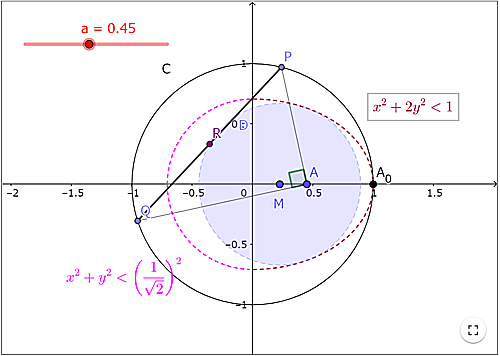画像ではこんな感じ

この$D$は⑵から，$$ \left(x-\frac{a}{2}\right)^2+y^2\lt \frac{2-a^2}{4} $$という不等式を得ます。つまり，$0< a< 1$の範囲でこの不等式を満たすような$a$が存在するための，点$(x,\,y)$の条件を求めれば良いわけです。

⑵より，領域$D$の内部及び境界線上の点$(x,\,y)$は次の条件を満たす。$$ \left(x-\frac{a}{2}\right)^2+y^2\lt \frac{2-a^2}{4} $$これを変形すると，$$ (a-x)^2+2y^2+x^2-1\lt 0 $$となる。この不等式を満たし，かつ$0\lt a\lt 1$を満たすような$a$が存在する$(x,\,y)$の条件を求める。
$f(a)= (a-x)^2+2y^2+x^2-1$とする。（$0\leq a\leq 1$）

さて，この$f(a)$は，$x$や$y$を固定して考えれば，$\pmb{a}$に関する２次関数だと思うことが出来ます。
ですから，「$0< a< 1$のときに，$f(a)< 0$を満たすような$a$が存在するための条件」を考えればよいです。
言い換えれば，「$0\leq a\leq 1$のときに，$f(a)$の最小値が$0$より小さければよい」ことに気づきます。つまり，２次関数の最小値を考えればよく，頂点の$x$座標によって場合分けをしていかなければなりません。それを念頭に，解答の続きを見ていきましょう。

①　$x < 0$のときは，$f(0)< 0$を満たすことが必要十分である。つまり，$$ 2y^2+2x^2-1\lt 0 $$$$ \therefore\quad x^2+y^2\lt \left( \frac{1}{\sqrt2} \right)^2 $$

②　$0\leq x\leq 1$のときは，$f(x)< 0$を満たすことが必要十分。つまり，$$ x^2+2y^2\lt 1 $$

③　$1< x$のときは，$f(1)< 0$を満たすことが必要十分だが，$$ f(1)=(x-1)^2+2y^2+(x^2-1) \geq 0 $$　　より，$1< x$のときには$f(a)< 0$となる$a$は，$0< a< 1$の範囲では存在しない。

①②③より，求める領域を図示すると以下のようになる。ただし境界線上は含まない。
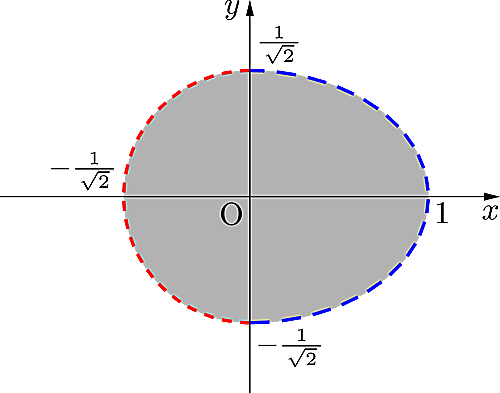卵みたい！
この領域の内部の面積を$S$をすると，
$$ \begin{align} S&=\text{（半径1の円の半分の面積）}+2\int_{0}^1\sqrt{\bunsuu{1-x^2}{2}}\,dx\\ &=\bunsuu{\pi}{2}+\sqrt2\int_0^1\sqrt{1-x^2}\,dx\\ &=\bunsuu{\pi}{2}+\bunsuu{\sqrt2\,\pi}{4}\\ &=\pmb{\bunsuu{\pi}{4}(\sqrt2+1)} \end{align} $$

おわりに

ここまで閲覧いただきありがとうございます。

この問題について

この問題は，河合塾が主催する〔東工大直前トライアル〕の問題を一部改変して作成しました。確かに，論理的な思考力が必要なので，大学入試に出てもおかしくないレベルだと思います。

この記事の元ネタ

https://marukunalufd0123.hatenablog.com/entry/2019/05/09/021109
1年以上前に上記の記事を書き，それをMathlogにて再編集しました。

類題を解きたい！

領域の通過領域に関する復習問題を出しておきます。これに解答することで，雰囲気をつかんでくれると嬉しいです。

復習用の類題

$(x-a)^2+y^2\leqq a-\bunsuu14\,\quad \cdots\cdots(\#)$について，$a$が$\bunsuu14\leqq a$を満たしながら動く時の，$(\#)$の通過領域を求めて図示しなさい。

正解は$y^2\leqq x$の部分です。答えを目指して変形してみてください。

GeoGebraとMathlog

本当はGeoGebraをこの記事に埋め込むことで，より直観的に分かりやすい記事が出来たのではないかと思うのですが，どうやらこのページでは
iframeがサポートされていないのか，残念ながら埋め込むことが出来ませんでした。今後もしもGeoGebraが埋め込めるようになれば，温めている幾何の話を書いてみようと思っています。

画像の投稿

今回用いた画像は，png形式で保存したものを用いました。ただ，Mathlogはすべての画像をjpg形式に直して貼り付けているようです。そのためかなり粗い画像となってしまっていますね。（それか，単に僕がPCの全画面で見ているからなのでしょうか）思わずデカッ！て突っ込みたくなりますね。11月14日追記：記事における画像の最大サイズが可変に改良されました。jpgの画像自体は，横500ピクセルで統一されているのかと推察します。

11月14日追記：現在のところですと，jpg形式またはpng形式の画像を読み込める？→読み込んだら一律で横500pxのjpg画像に変換する→それの見た目サイズを変化させている，ということを内部で行っていると推察します。そのため，画像がやや粗く見えるのは仕様です。