Bessel関数のFourier変換
今回はBessel関数のFourier変換ですが、半分がdelta関数の議論になります。
前提知識
Bessel函数の積分表示
delta関数の基本的な性質
第一種Chebyshev多項式(定義だけ知っていればOK)
注意
変換は後で定義します。物理などでよく扱うものとは少し異なります。
Bessel関数の添字は整数に限られています。僕の力不足です。
delta関数
変換前に、delta関数についての重要な性質があるのでそれを紹介しておきます。
$\displaystyle\delta(f(x))=\sum_{i}\frac{\delta(x-x_i)}{|f'(x_i)|}$
尚、$x_i$は$f$の零点とする。
これを証明するには積分を用いますが、少し準備をします。
準備
まず、$f$の$i$番目の極値から$i+1$番目の極値までの$x$の区間を$D_i$とし、$D_i$内に存在する$f$を$f_i$とする。
こうすると$f_i$は単調となるから、逆関数$f_i^{-1}$が書けますね。
具体例を見ましょう。
例えば$f(x)=\sin{x}$の時はこんな感じです。(図1)
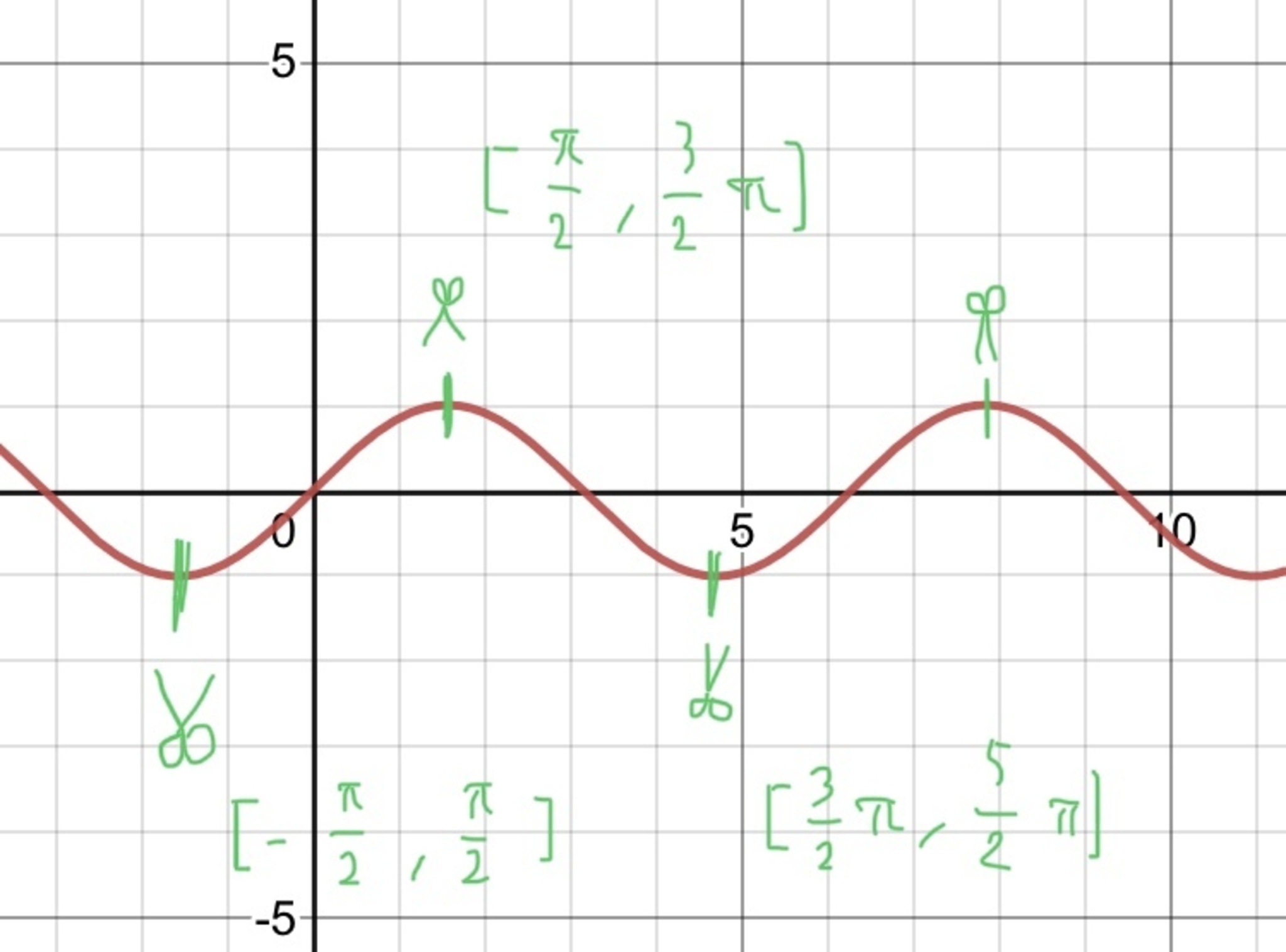図1
緑色で描いたリボンみたいなのは一応ハサミです。極値で切断するわけです。
この場合$D_i$は、図にもある通り、$\displaystyle[-\frac{\pi}{2},\frac{\pi}{2}],[\frac{\pi}{2},\frac{3}{2}\pi],…$と続きます(もちろん左にも続く)。
この後$\displaystyle f_i(D_i)$が出てきますが、これは$y=f_i(t)$と変数変換したあとの積分区間とします。こんな記法ダメかも知れませんが、ご了承ください。
$\displaystyle\begin{eqnarray}
\delta(f(x)) &=& \int_{-∞}^∞\delta(f(t))\delta(x-t)dt \\
&=& \sum_{i}\int_{D_i}\delta(f_i(t))\delta(x-t)dt \\
&=& \sum_{i}\int_{f_i(D_i)}\delta(y)\delta(x-f_i^{-1}(y))\frac{dy}{|f'(f_i^{-1}(y))|} \\
&=& \sum_{i}\frac{\delta(x-f_i^{-1}(0))}{|f'(f_i^{-1}(0))|} \\
&=& \sum_{i}\frac{\delta(x-x_i)}{|f'(x_i)|}
\end{eqnarray}$
$f_i$が単調増加でも単調減少でも成り立つように途中で絶対値を取りました。
補足1
$f_i$が零点を持たない場合、つまり$f_i^{-1}(0)$が存在しない場合は(図2の右側)、処理出来てないじゃないか、と思う方もいらっしゃると思います。しかし、零点を持たない場合は、積分区間$\displaystyle f_i(D_i)$は0をまたがらないと言えます。その間delta関数がずっと0ですから、積分の結果は0となるのでOKです。
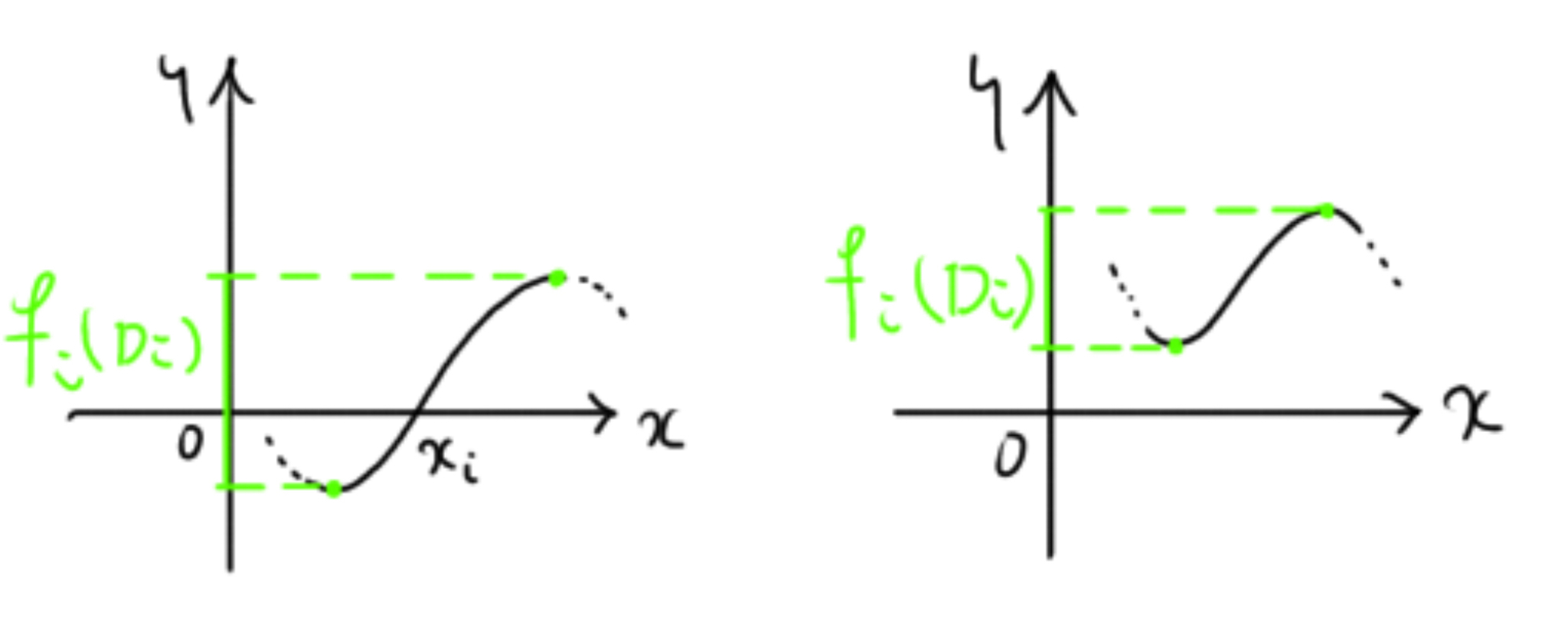fの挙動と値域
補足2
$f$は出てきた積分が収束してくれるような連続関数であれば構わないと思うのですが、あまり自信がないのでコメントなどでどなたか補足してくださると助かります。
Fourier変換
下準備も出来ましたので、いよいよFourier変換です。
$\displaystyle\mathcal{F}\left[f(x)\right](\xi):=\int_{-∞}^∞f(x)\exp{(-2\pi ix\xi)}dx$
定義をこれにしたのにはわけがあります。僕が好きだからです。
$\displaystyle\mathcal{F}\left[J_n(x)\right]=\frac{2(-i)^nT_n(2\pi\xi)}{\sqrt{1-(2\pi\xi)^2}}\mathrm{rect}(\pi\xi)$
初めに、矩形関数に注目します。これは$\displaystyle|\xi|>\frac{1}{2\pi}$では0になりますから、$\displaystyle|\xi|\leq\frac{1}{2\pi}$の範囲だけを考えたらいいですね。
$\displaystyle\begin{eqnarray}
\mathcal{F}\left[J_n(x)\right] &=& \int_{-∞}^∞\int_{-\pi}^\pi\exp{\big(ix\sin{\theta}-in\theta\big)}d\theta\exp{(-2\pi ix\xi)}dx \\
&=& \int_{-\pi}^\pi\int_{-∞}^∞\exp{\big(\!-\!2\pi ix\big(\xi-\frac{\sin{\theta}}{2\pi}\big)\big)}dx\exp{(-in\theta)}d\theta \\
&=& \int_{-\pi}^\pi\delta\big(\xi-\frac{\sin{\theta}}{2\pi}\big)\exp{(-in\theta)}d\theta \\
&=& \int_{-\pi}^\pi\sum_{i=1}^2\frac{\delta(\theta-\theta_i)}{\frac{1}{2\pi}\sqrt{1-(2\pi\xi)^2}}\exp{(-in\theta)}d\theta \\
&=& \frac{2}{\sqrt{1-(2\pi\xi)^2}}\big(\exp{(-in\theta_1)+\exp{(-in\theta_2)}}\big) \\
&=& \frac{2}{\sqrt{1-(2\pi\xi)^2}}\exp{\big(\!-\!\frac{\pi}{2}in\big)\cos{\big(n\big(\frac{\pi}{2}-\theta_1\big)\big)}} \\
&=& \frac{2(-i)^nT_n(2\pi\xi)}{\sqrt{1-(2\pi\xi)^2}}
\end{eqnarray}$
ここで、$\displaystyle\theta_1=\sin^{-1}{2\pi\xi},\quad\theta_2=\pi-\theta_1$です。
解説は以上です。ありがとうございました。
この記事を高評価した人
この記事に送られたバッジ
投稿者
