2のn乗の数列の最上位桁の数を調べる

$a_{n} := 2^{n}$からなる数列$\left\{a_{n}\right\}_{n=1}^{N}$について考えます。

例えば、$N = 5$のとき、$\left\{a_{n}\right\}_{n=1}^{5} = 2, 4, 8, 16, 32.$です。$N$がある程度大きいときの挙動を見たいので、Python言語でプログラミングをしてみましょう。

$N = 100$のとき、

      N = 100
a = [2 ** i for i in range(1, N + 1)]
print(a)
    

というPythonプログラムを実行すれば、

      [2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576, 2097152, 4194304, 8388608, 16777216, 33554432, 67108864, 134217728, 268435456, 536870912, 1073741824, 2147483648, 4294967296, 8589934592, 17179869184, 34359738368, 68719476736, 137438953472, 274877906944, 549755813888, 1099511627776, 2199023255552, 4398046511104, 8796093022208, 17592186044416, 35184372088832, 70368744177664, 140737488355328, 281474976710656, 562949953421312, 1125899906842624, 2251799813685248, 4503599627370496, 9007199254740992, 18014398509481984, 36028797018963968, 72057594037927936, 144115188075855872, 288230376151711744, 576460752303423488, 1152921504606846976, 2305843009213693952, 4611686018427387904, 9223372036854775808, 18446744073709551616, 36893488147419103232, 73786976294838206464, 147573952589676412928, 295147905179352825856, 590295810358705651712, 1180591620717411303424, 2361183241434822606848, 4722366482869645213696, 9444732965739290427392, 18889465931478580854784, 37778931862957161709568, 75557863725914323419136, 151115727451828646838272, 302231454903657293676544, 604462909807314587353088, 1208925819614629174706176, 2417851639229258349412352, 4835703278458516698824704, 9671406556917033397649408, 19342813113834066795298816, 38685626227668133590597632, 77371252455336267181195264, 154742504910672534362390528, 309485009821345068724781056, 618970019642690137449562112, 1237940039285380274899124224, 2475880078570760549798248448, 4951760157141521099596496896, 9903520314283042199192993792, 19807040628566084398385987584, 39614081257132168796771975168, 79228162514264337593543950336, 158456325028528675187087900672, 316912650057057350374175801344, 633825300114114700748351602688, 1267650600228229401496703205376]
    

のように、$\left\{a_{n}\right\}_{n=1}^{100}$の値が簡単に得られます。

次に、この数列に関して、

• $16 \rightarrow 1$
• $512 \rightarrow 5$
• $2048 \rightarrow 2$

のような最上位桁の数が何であるのかについて、数え上げてみます。
上のプログラムに続けて

      import numpy as np
counter = np.zeros(10)

for x in a:
    index = int(str(x)[0])
    counter[index] += 1

for (i, x) in enumerate(counter):
    print(f"{i}: {x:.0f}")
    

と実行すれば、(各数字を文字列として見て、1番最初の文字を数値に変換しています。)

      0: 0
1: 30
2: 17
3: 13
4: 10
5: 7
6: 7
7: 6
8: 5
9: 5
    

のように結果が得られます。最上位の桁が1のものが一番多く、大きくなるにつれて少なくなっていることがわかります。

次に、この結果を棒グラフにしてみます。上のプログラムに続けて

      import matplotlib.pyplot as plt

plt.xlim(0, 10.0)
plt.ylim(0, 0.34)
plt.bar(np.arange(1, 10), counter[1:10]/N, tick_label=np.arange(1, 10), alpha=0.8)

plt.show()
    

と実行すれば、

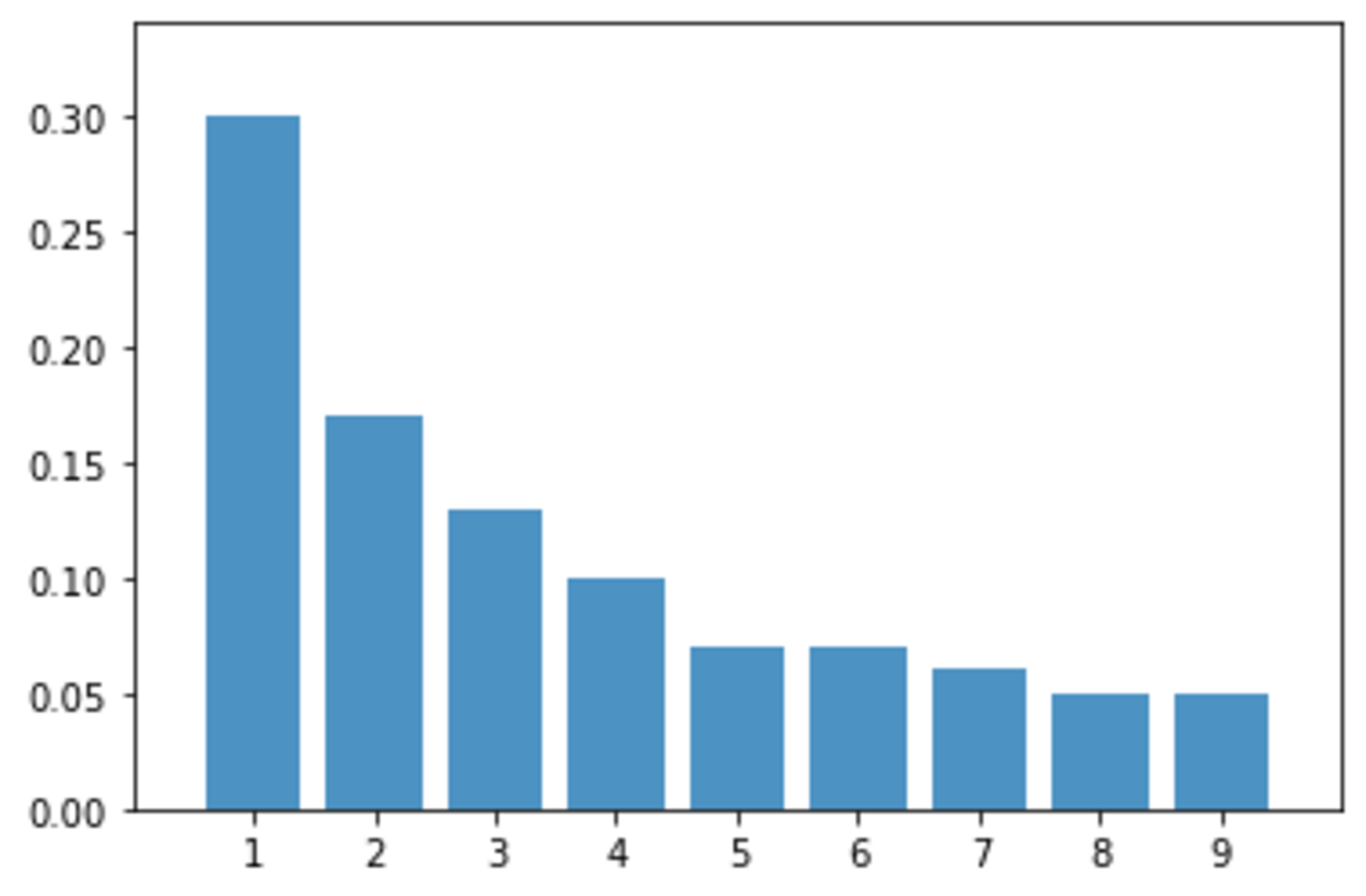
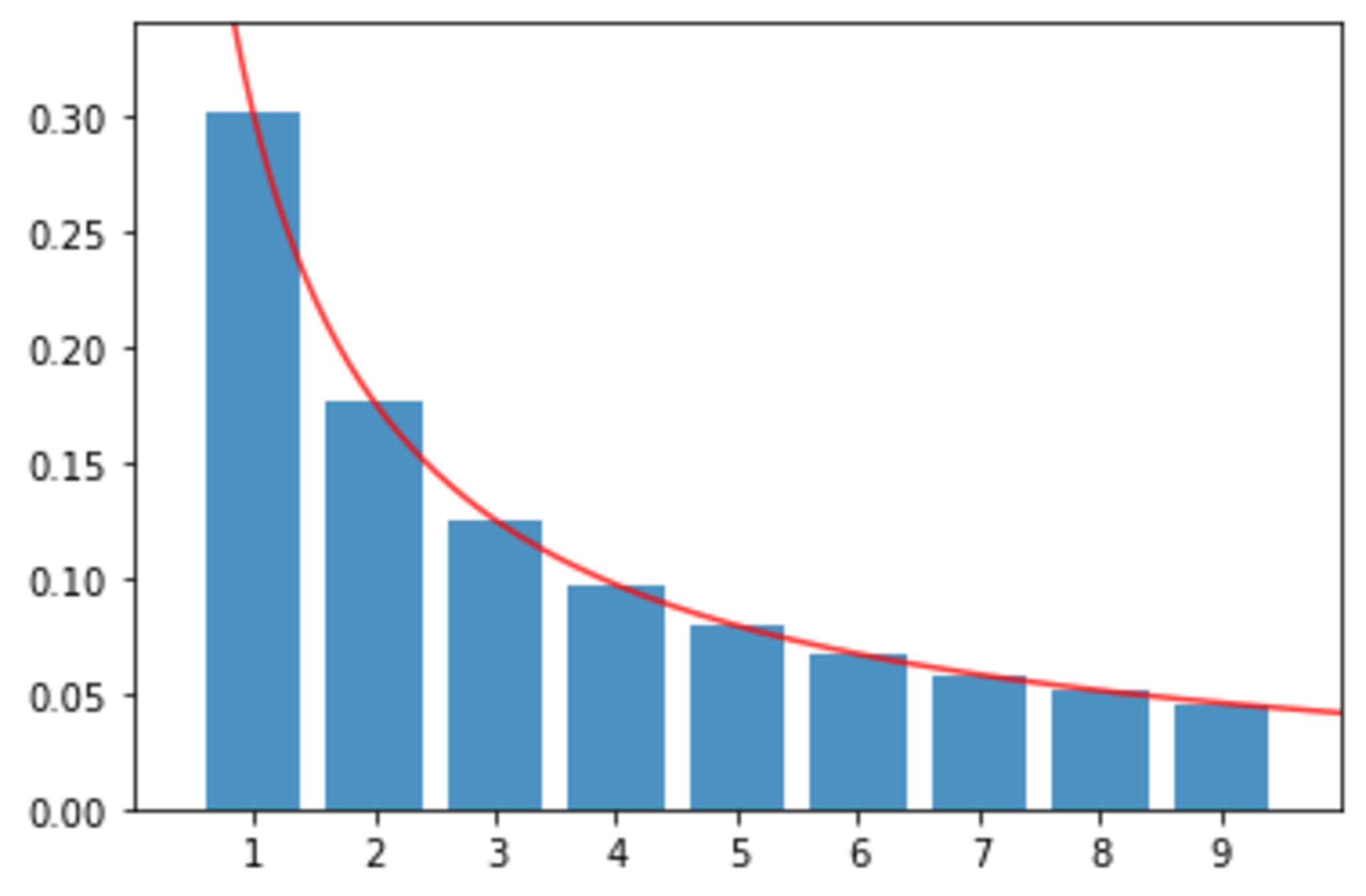
とグラフが得られます。ここで、グラフの縦軸は、N全体に対する割合です。たとえば、最上位桁が$1$である$a_{n}~(すなわち、a_{4} = 16,~ a_{7} = 128,~ a_{64} = 18446744073709551616など)$が約3割であり、最上位桁が$4$である$a_{n}~(すなわち、a_{12} = 4096,~ a_{22} = 4194304,~ a_{52} = 4503599627370496など)$が約1割であることなどがわかります。

さて、上の分布は何に従っているのでしょうか。$\log_{10}2 \sim 0.301, \log_{10}1.5 = \log_{10}3 - \log_{10}2 \sim 0.176$ですし、なんだか$y=\log_{10}\frac{x+1}{x}$に近い気がするので、上の棒グラフに重ねて描画してみましょう。

      import matplotlib.pyplot as plt
import numpy as np

N = 100
a = [2 ** i for i in range(1, N + 1)]
counter = np.zeros(10)

for x in a:
    index = int(str(x)[0])
    counter[index] += 1


plt.xlim(0, 10.0)
plt.ylim(0, 0.34)
plt.bar(np.arange(1, 10), counter[1:10]/N, tick_label=np.arange(1, 10), alpha=0.8)

x = np.linspace(0.1, 10.0, 1000)
plt.plot(x, np.log10((x+1)/x), color='red', alpha=0.8)

plt.show()
    

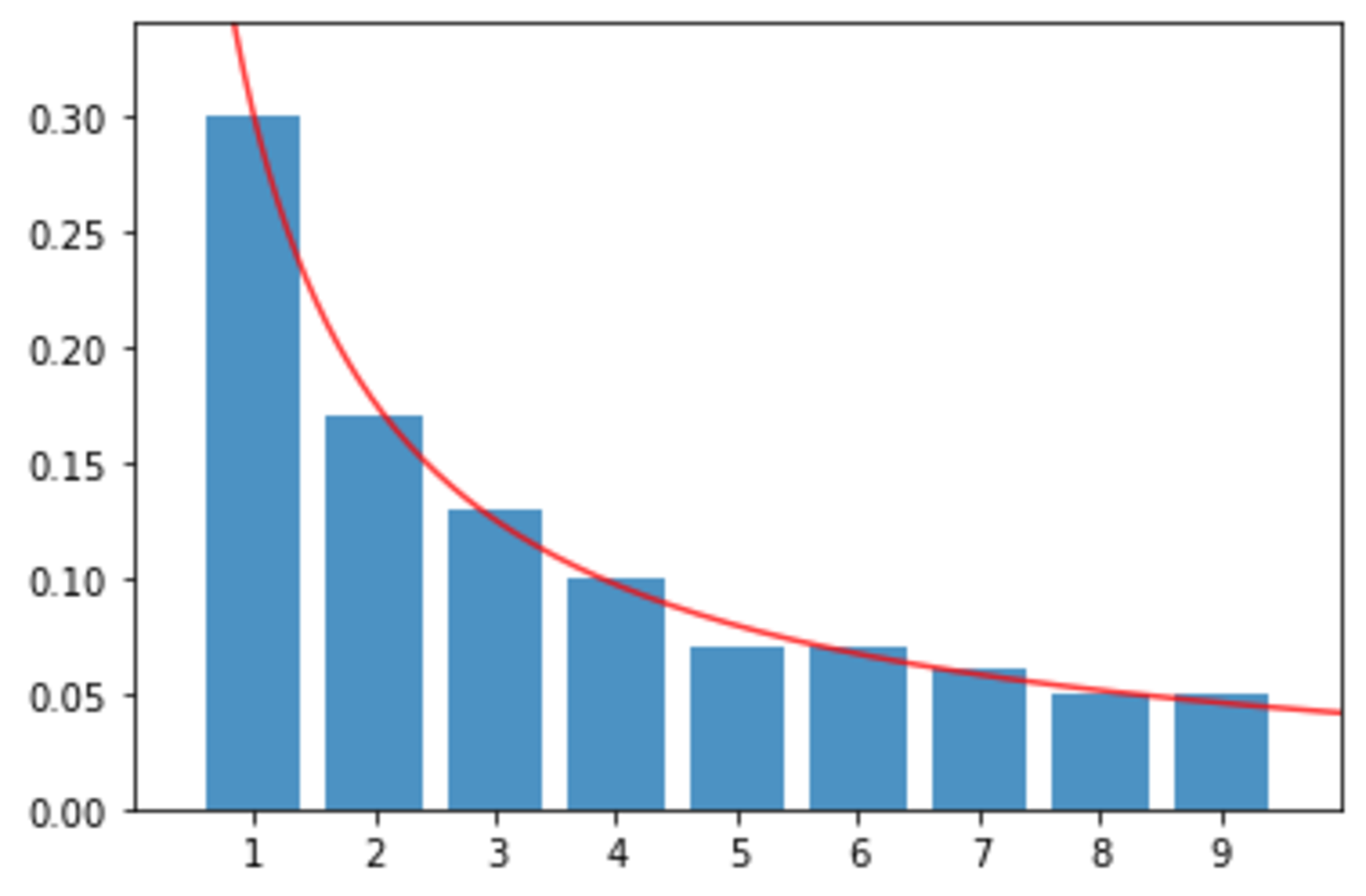
良さそうな気がします。

また、$N$を変えて実行してみると、$N$が大きいほど、2つのグラフの取る値が近づいていく気もします。

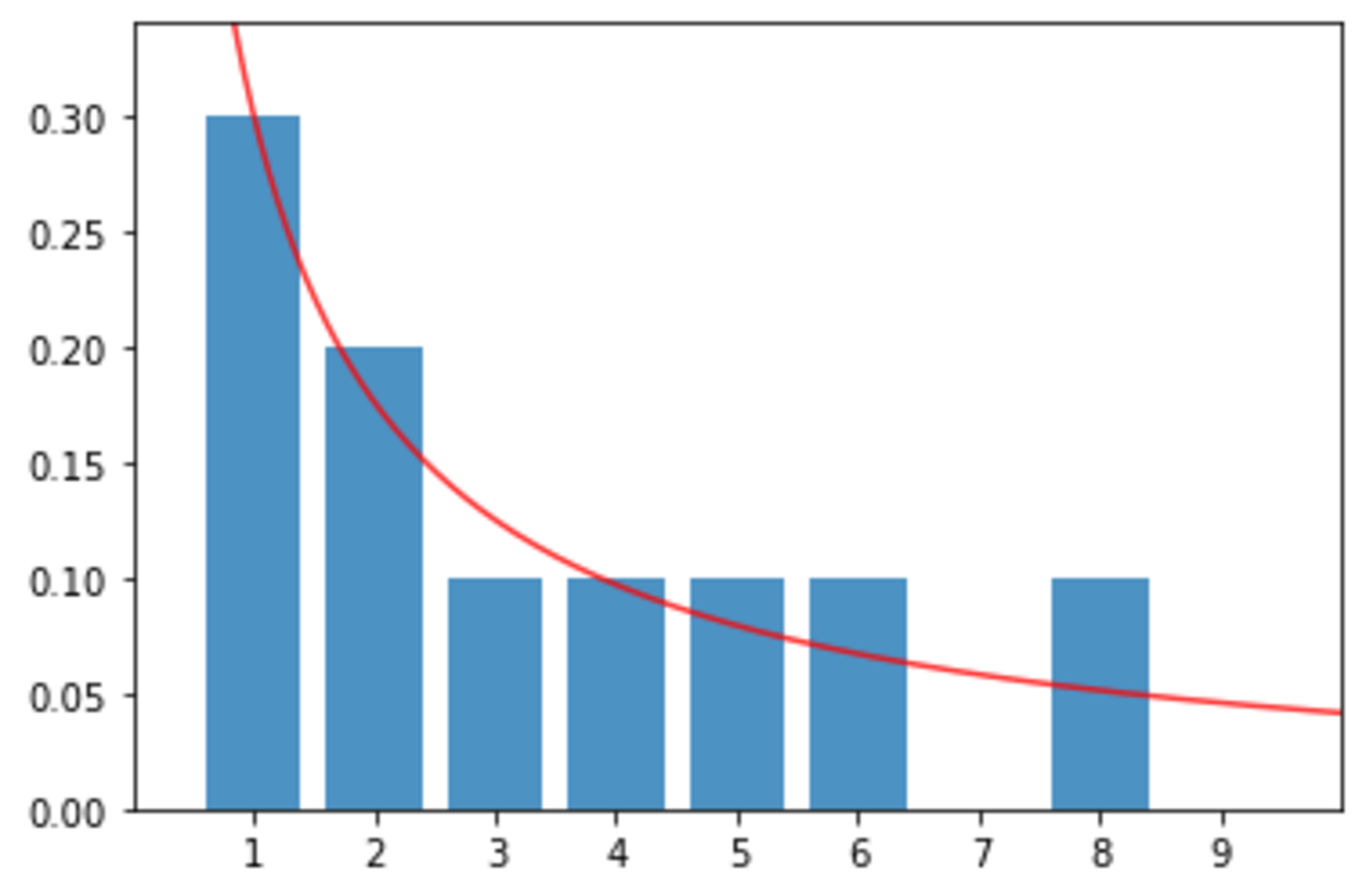N = 10

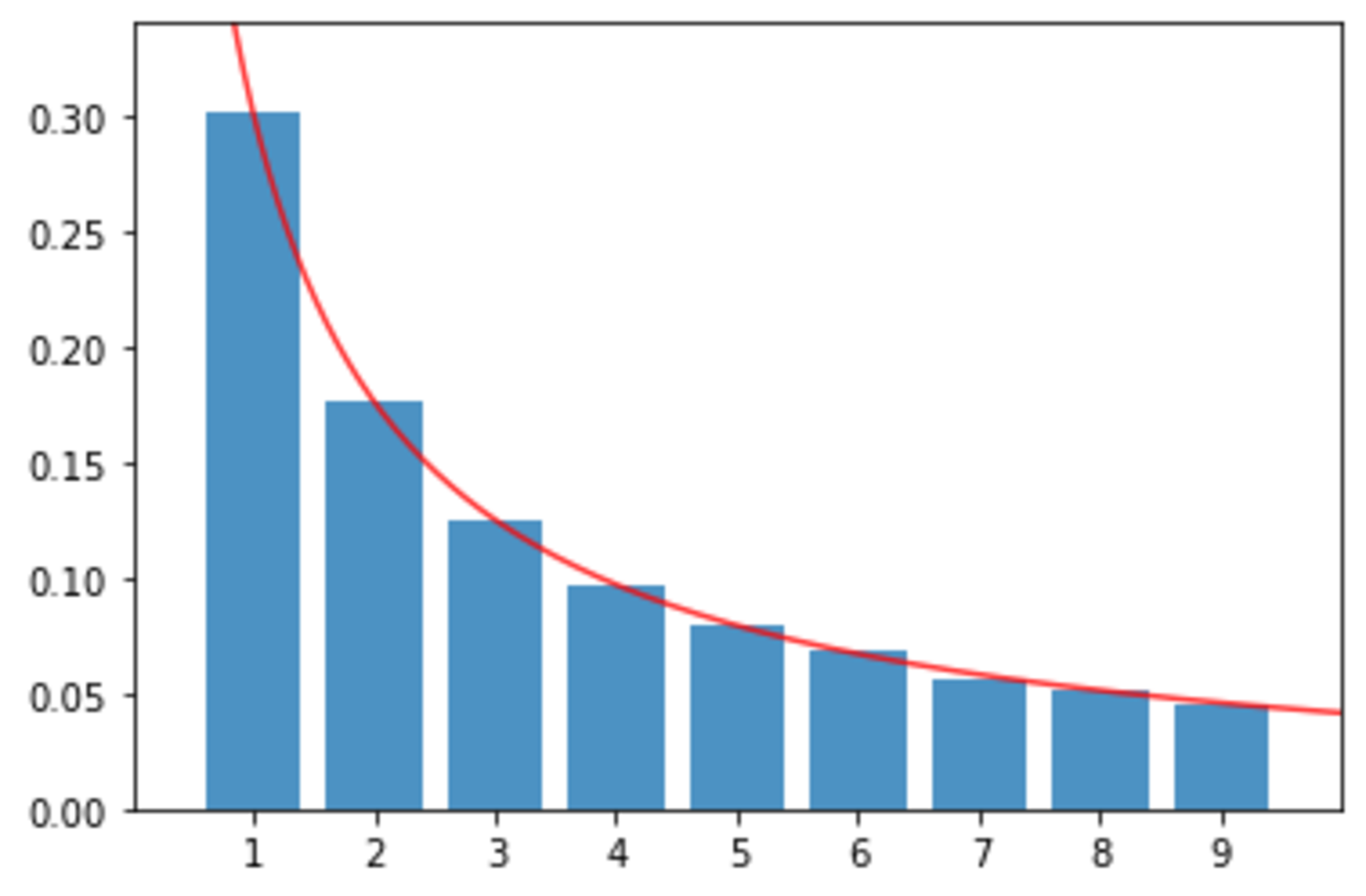N = 1000

N = 10000

実際、数式として次が成り立ちます。（等式の左辺が棒グラフ、右辺が曲線のグラフに対応しています。）