【相対論】Gödel宇宙の基本事項の解説
この記事はGödel宇宙の入門記事です。Gödel宇宙に関して次のことを解説します。
- Gödel宇宙の幾何学的なモデルの構成
- 時間的閉曲線の存在
- Einstein方程式の厳密解であること
- 3つのよく使われる座標系間の座標変換とその幾何学的な仕組み
リーマン幾何は既知とします。また関連するキーワードとして
- Ricciテンソルの$1+n$分解
- Bianchi-Cartan-Vranceanu空間族
があります。
リーマン幾何や相対論の初歩を学んだ人でGödel宇宙について基本事項を勉強したい人の役に立てばと思います。計算が結構ややこしいので計算ミスしてたら教えてください。
イントロ
Gödel宇宙は1949年にKurt Gödelにより発表された一般相対論における厳密解です。正確には回転する流体を物質とする宇宙項を持つEinstein方程式の厳密解です。最大の特徴は因果構造の異常さであり、局所的に未来過去の区別はありますが（時間的向き付け可能）、大域的には未来と過去の区別がなく、時間旅行が可能な時空となっています。
このノートの構成は以下です。初めにGödel宇宙の幾何学モデルを構成し時間的閉曲線の存在について解説します。Gödel宇宙のモデルを構成する際の座標は用途に応じて色々あると思いますが、有名なものとして3つの座標を紹介します。このノートではHolocycle based座標とHyperbolic model based座標とPoincare model based座標呼ぶことにします。Holocycle based座標とHyperbolic model based座標が物理ではよく使われますが、Poincare model based座標が幾何学的に理解しやすい気がするのでPoincare model based座標を主に使って解説します。またGödel宇宙がEinstein系の解になっていることを確かめます。最後にHolocycle based座標とHyperbolic model based座標とPoincare model based座標の座標変換やその幾何学的な仕組みを簡単に述べます。いくつかの簡単な命題に関しては演習問題としましたが、解答は後の方に載せています。また参考文献についての簡単な説明も書いています。
この記事を通して微分形式の内積はHodge starの定義で使用する内積を使います。
Gödel宇宙の構成と時間的閉曲線
ここではGödel宇宙の計量をPoincare model based座標で構成し時間的閉曲線の存在について解説します。
モデルの構成
まず2次元Euclid空間の計量を極座標で表示すると
$
\begin{align}
ds^2=dr^2+r^2d\theta^2
\end{align}
$
です。さらにこれを負に曲げます。すなわち2次元の双曲空間にします。
$
\begin{align}
ds^2=\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2},\ (K<0)
\end{align}
$
ただし、$r^2<-\frac{4}{K}=\frac{4}{|K|}$の開円板が定義域で、負の定数$K$はこの双曲空間のガウス曲率です。これはポアンカレディスクとも呼ばれ、円盤の境界$r^2=\frac{4}{|K|}$は無限遠です。双曲空間はEuclid空間よりも“広い”空間です。
さらにここに時間を加え3次元の時空にします。
$
\begin{align}
ds^2=-dt^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}
\end{align}
$
この時空は静的といい、ディスクは“静止”しています。そこでディスクを“回転”させます。
$
\begin{align}
ds^2=-\left(dt+f(r,\theta)d\theta\right)^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}
\end{align}
$
この計量がなぜ回転っぽいかというと、$\partial_t$と$\partial_\theta$はもはや直交せず、従って$\partial_t$を$t=$一定面に射影したベクトルは$\theta$成分を持っているからです。
さらに$f(r,\theta)$を適当に決めて“回転量”が一定になるようにします。つまり$\partial_t$のrotationの大きさの2乗が$||{\rm rot}(\partial_t)||^2=\omega^2={\rm const.}$となるようにしたいということです。このためには
$$f(r,\theta)=\frac{\omega}{2}\frac{r^2}{1+\frac{K}{4}r^2}$$
とすればよいです。これを確かめることは演習問題にします。
計量が
$$ds^2=-\left(dt+\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2}\right)^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}$$
で与えられるリーマン多様体において、$||{\rm rot}(\partial_t)||^2=\omega^2$となることを示せ。
最後に1次元空間をリーマン直積で付け加えて次のように4次元の時空にします。
$$
\begin{align}
ds^2=-\left(dt+\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2}\right)^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}+dz^2
\end{align}
$$
この座標をPoincare model based座標と呼びます。後で分かるようにこのような時空でEinstein方程式の解になるのは$K=-\omega^2/2$のときに限ります。このときこの時空をGödel宇宙といいます。しかし因果構造と回転量と曲率のおもしろい関係を理解するために一旦$K=-\omega^2/2$を仮定せずに解説を進めます。またこのようにすればGödel宇宙を2パラメータ時空族の特別な場合として捉えることができるので幾何学的にもより進んだ理解となります。
時間的閉曲線
ではGödel宇宙には時間的閉曲線が存在することを見ましょう。用語の復習をしておきます。接ベクトル$X\in T_pM$が時間的であるとは$||X||^2=g(X,X)<0$となることです。また時間的曲線とは区分的$C^1$曲線で接ベクトルが常に時間的となっている曲線のことです。有質量の粒子の世界線は時間的曲線になります。これは任意の観測者が観測する有質量粒子の相対速度が光速より小さいことと同値です。時間的閉曲線が存在する場合、その曲線に沿って未来向きに進んでいると時空の同じ点に戻ってくるということを意味します。相対論においては時間的閉曲線をタイムマシンとも言ったりします。
Gödel宇宙において、$t=$一定面上に誘導される計量は以下のようになります。
$$
\begin{align}
ds^2&=\frac{dr^2}{(1+\frac{K}{4}r^2)^2}+\left(\frac{r^2}{(1+\frac{K}{4}r^2)^2}-\frac{\omega^2}{4}\frac{r^4}{(1+\frac{K}{4}r^2)^2}\right)d\theta^2+dz^2 \\
&=\frac{dr^2}{(1+\frac{K}{4}r^2)^2}+\frac{r^2(1-\frac{\omega^2}{4}r^2)}{(1+\frac{K}{4}r^2)^2}d\theta^2+dz^2
\end{align}
$$
これより、$t=$一定面上において、$||\partial_\theta||^2=\frac{r^2(1-\frac{\omega^2}{4}r^2)}{(1+\frac{K}{4}r^2)^2}$であると分かります。よって$r^2<\frac{4}{\omega^2}$のときは$||\partial_\theta||^2>0$となり空間的となりますが、$r^2>\frac{4}{\omega^2}$という領域が存在すれば、$||\partial_\theta||^2<0$となり時間的となります。$\theta$のみを変化させる曲線（$\theta-$曲線）は閉曲線なので、このときは時間的閉曲線が存在することになります。
$r^2>\frac{4}{\omega^2}$という領域が存在するかどうかは時空の回転力によります。というのもこの時空は$r^2<\frac{4}{|K|}$の領域で考えていますから、$\frac{4}{\omega^2}<\frac{4}{|K|}$のとき、すなわち$|K|<\omega^2$のときしかこういう領域は存在しません。$0\le\omega^2\le|K|$のときは時空がゆっくり回っていて時間的閉曲線は存在しません。よって時空の回転力がポアンカレディスクの曲率（の絶対値）を超えた時に時間的閉曲線が出現するということになります。
実は後で分かるようにEinstein方程式の解になるのは$K=-\omega^2/2$のときに限ります。なのでGödel宇宙には常に時間的閉曲線が存在します。
普通は$\omega^2\le|K|$のときはGödel宇宙と呼ばないですが、文脈によってはGödel type metricと呼ぶことがあります（一般にノルムが一定かつツイストが0でない時間的Killingベクトル場が存在する時空の計量をGödel type metricと呼びます。）。図１はこの様子を$(r,\theta)$面で俯瞰したものです。
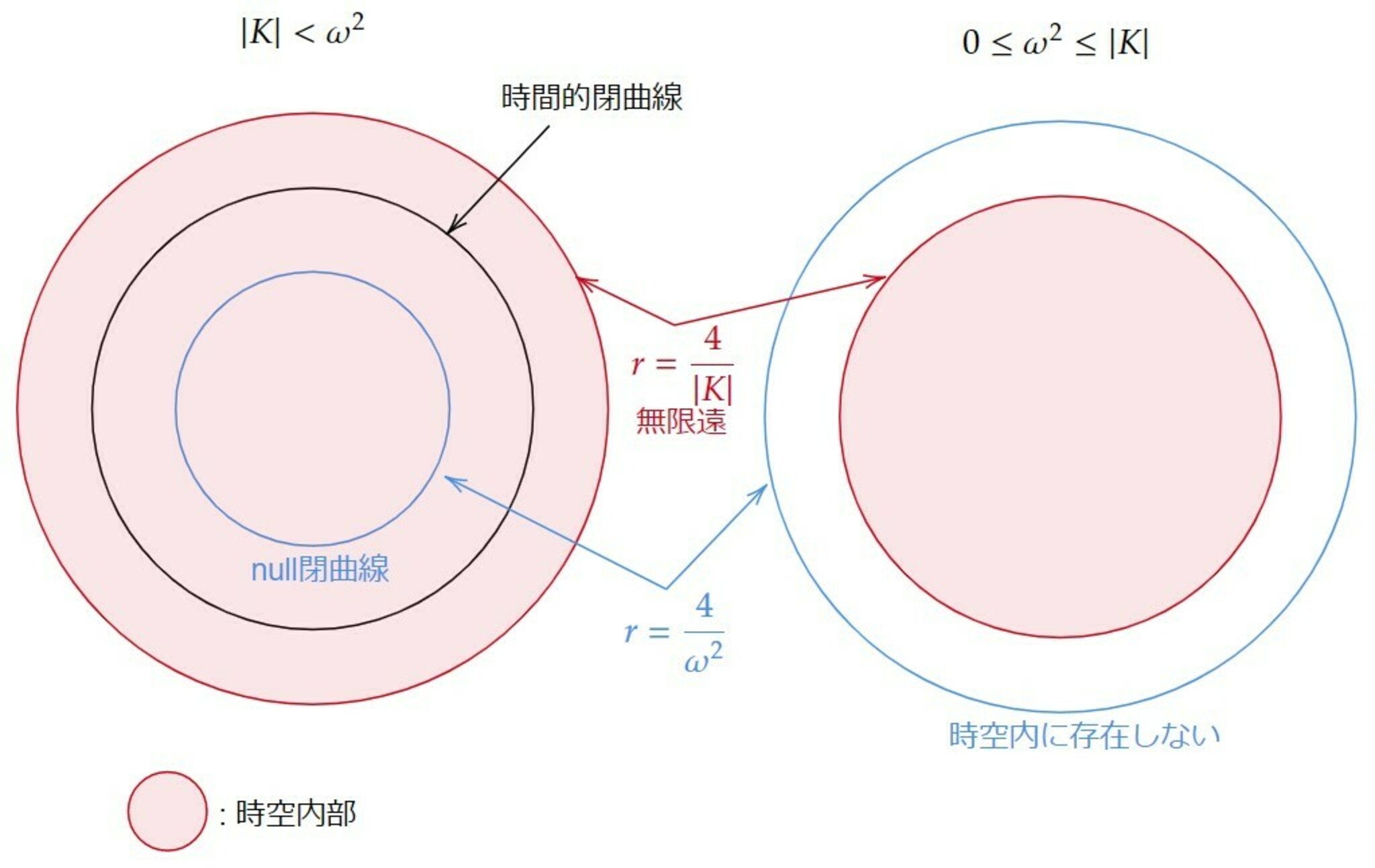Gödel宇宙の俯瞰図
余談ですが、$\omega^2=-K$のとき$z$方向以外の3次元時空の部分
$
\begin{align}
ds^2=-\left(dt+\frac{\omega}{2}\frac{r^2d\theta}{1-\frac{\omega^2}{4}r^2}\right)^2+\frac{dr^2+r^2d\theta^2}{(1-\frac{\omega^2}{4}r^2)^2}
\end{align}
$
は負の定曲率空間となり、3次元anti-de Sitter時空（$AdS_3$）と呼ばれます。実際$Ric=-\frac{\omega^2}{2}g$であることが確かめられます。つまり回転力がポアンカレディスクの曲率の絶対値と等しいとき、元の4次元時空は$AdS_3\times\mathbb{R}$となります。
また3次元リーマン多様体
$$
ds^2=\left(dt+\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2}\right)^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}
$$
は2つのパラメータ$\omega,K$で特徴付けられるリーマン多様体の族でBianchi-Cartan-Vranceanu空間族と呼ばれ、Thurston幾何、Bianchi分類、ユニモジュラーLie群の幾何の文脈で重要です（文献[1]）。このBianchi-Cartan-Vranceanu空間族のLorentz類似物に空間を1次元加えて4次元時空族にしたものの特別な場合がGödel宇宙や$AdS_3\times\mathbb{R}$です。
Einstein系の厳密解であることの確認
まず一般相対論の復習をします。
$(M,g)$を時空(時間的向き付けられたLorentz多様体)とし、$u\in\mathcal{X}(M)$を$||u||^2=-1$となるtimelikeベクトル場、$\rho,P\in C^\infty(M)$を非負スカラー関数、$\Lambda\in\mathbb{R}$とする。
このとき$(u,\rho,P)$が完全流体であるとは
$$
\begin{align}
u(\rho)&=-(\rho+P)div(u),\\
(\rho+P)\nabla_uu&=-grad(P)^\perp,
\end{align}
$$
を満たすときのことを言う。ここで$grad(P)^\perp:=grad(P)+g(u,grad(P))u$は$grad(P)$の$u$に直交する成分である。$u$は4元流速場、$\rho$はエネルギー密度、$P$は(等方)圧力と呼ばれます。さらに完全流体$(u,\rho,P)$のエネルギーテンソルは
$$
T=\rho u\otimes u+P(g+u\otimes u),
$$
で与えらる。
$(M,g,u,\rho,P)$が物質を完全流体$(u,\rho,P)$とする宇宙項を持つEinstein系の厳密解であるとは
$$
Ric-\frac{1}{2}Rg+\Lambda g=T,
$$
を満たすときのことを言う。これをEinstein方程式と呼ぶ。
4次元のEinstein方程式は
$$
Ric=T-\frac{1}{2}Tr(T)g+\Lambda g
$$
としても同値であることを示せ。
それではGödel宇宙のPoincare model based座標での計量
$$
ds^2=-\left(dt+\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2}\right)^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}+dz^2
$$
が完全流体と宇宙項を持つEinstein系の厳密解であることを見ます。
まず物質である完全流体ですが、$u=\partial_t$とし、$\rho,P(>0)$は定数とします。このとき$u$はノルムが一定のKillingベクトル場なので$\nabla_uu=0$となります（演習問題）。またKillingベクトル場はdigergence freeであり、$P,\rho$は定数なので完全流体の運動方程式
$$
\begin{align}
u(\rho)&=-(\rho+P)div(u),\\
(\rho+P)\nabla_uu&=-grad(P)^\perp,
\end{align}
$$
が満たされます。
$(M,g)$を擬リーマン多様体、$\xi$をKillingベクトル場とする。$||\xi||^2={\rm const.}$であるとき、$\nabla_\xi\xi=0$であることを示せ。
次にEinstein方程式を確認しましょう。初めにRicciテンソルを計算しますが、この計算はRicciテンソルの$1+n$分解の公式を使うと簡単です。ただしこの公式の導出はかなりめんどうなのでここでは認めることにします（別の記事で導出するかもしれません）。
$(N,h)$をリーマン多様体とし、$M=\mathbb{R}\times N$とする。$\eta\in A^1(N)$を$N$上の１形式とし、$M$のLorentz計量を
$$
g=-(dt+\eta)^2+h
$$
とする。ここで$t$は$\mathbb{R}$の座標である。$\Omega=d\eta\in A^2(N),u=\partial_t$とし、$\pi:M\to N$を$u$が生成する等長変換に関するリーマン沈め込みとする。このとき、
$$
Ric_M=\pi^\ast Ric_N+\frac{1}{2}\pi^\ast\Omega_2+2\pi^\ast(div_N\Omega)\vee {}^\flat u+\frac{1}{2}\pi^\ast||\Omega||^2_h{}^\flat u\otimes {}^\flat u
$$
が成り立つ。ここで$\vee$は対称テンソル積である。また$\Omega_2$は$N$上の2階対称共変テンソル場であり、$(\Omega_2)_{ij}:=\Omega_{ik}\Omega_j^{\ k}$で与えられる(文献[4])。
この公式を
$$
\begin{align}
ds^2=-\left(dt+\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2}\right)^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}+dz^2
\end{align}
$$
に適用しましょう。$z$方向はリーマン直積なので考える必要がありません。なので$M$を3次元時空
$$
\begin{align}
ds^2=-\left(dt+\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2}\right)^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}
\end{align}
$$
とし、$N$を2次元の双曲空間
$$
\begin{align}
ds^2=\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}
\end{align}
$$
とし、
$$
\eta=\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2},
\ \Omega=d\eta=\omega\frac{rdr\wedge d\theta}{(1+\frac{K}{4}r^2)^2}
$$
として公式１を適用します。$M$の正規直交フレームを$\{u,e_1,e_2\}$とすると、このフレームに関して
$$
\pi^\ast Ric_N={\rm diag}(0,K,K)
$$
となります。また$\Omega$が$N$の体積形式に比例していることを考えれば、
$$
\pi^\ast\Omega_2={\rm diag}(0,\omega^2,\omega^2),\ div_N\Omega=0,\ \pi^\ast||\Omega||^2_h=\omega^2
$$
となります（演習問題）。
$(M,g)$を2次元リーマン多様体とし、$\Omega$を体積形式とする。このとき、$\Omega_2=g,\ div\Omega=0$であることを示せ。
よって公式１を使うと、$M$の正規直交フレームを$\{u,e_1,e_2\}$に関して、
$$
Ric_M={\rm diag}(\frac{\omega^2}{2},K+\frac{\omega^2}{2},K+\frac{\omega^2}{2})
$$
となります。従って、Gödel宇宙の正規直交フレームを$\{u,e_1,e_2,\partial_z\}$として、これに関してRicciテンソルは
$$
Ric={\rm diag}(\frac{\omega^2}{2},K+\frac{\omega^2}{2},K+\frac{\omega^2}{2},0)
$$
となります。
完全流体のエネルギーテンソルは、正規直交フレーム$\{u,e_1,e_2,\partial_z\}$に関して
$$
T={\rm diag}(\rho,P,P,P)
$$
となるので、
$$
\begin{align}
&T-\frac{1}{2}Tr(T)g+\Lambda g\\
=&{\rm diag}(\rho,P,P,P)-\frac{3P-\rho}{2}{\rm diag}(-1,1,1,1)+\Lambda{\rm diag}(-1,1,1,1)\\
=&{\rm diag}(\frac{\rho+3P}{2}-\Lambda,\frac{\rho-P}{2}+\Lambda,\frac{\rho-P}{2}+\Lambda,\frac{\rho-P}{2}+\Lambda)
\end{align}
$$
となります。よってEinstein方程式
$$
Ric=T-\frac{1}{2}Tr(T)g+\Lambda g
$$
より
$$
\begin{align}
\frac{\omega^2}{2}&=\frac{\rho+3P}{2}-\Lambda,\\
K+\frac{\omega^2}{2}&=\frac{\rho-P}{2}+\Lambda,\\
0&=\frac{\rho-P}{2}+\Lambda
\end{align}
$$
を得ます。これを解くと
$$
\begin{align}
\Lambda&=-\frac{\rho-P}{2},\\
\omega^2&=2(\rho+P),\\
K&=-\frac{\omega^2}{2}=-(\rho+P)
\end{align}
$$
となります。このことから完全流体が重力源の物質となるEinstein系の厳密解としてGödel宇宙が得られました。
Holocycle based座標とHyperbolic model based座標
Gödel宇宙のよく使われる座標としてHolocycle based座標とHyperbolic model based座標があります。Poincare model based座標の方が幾何学的に理解しやすいと思ったのでこれまではPoincare model based座標で説明してきましたが、おそらくHolocycle based座標とHyperbolic model based座標の方がよく使われるので、入門者はこれらの座標の関係を理解しておくべきだと思われます。少し計算を頑張る必要がありますが、幾何学的な仕組みを理解していれば何も見なくても再現はできます。
Hyperbolic model based座標とPoincare model based座標の関係
この２つの関係は単純で慣れていればほぼ同じに見えます。まず座標$\rho$を$\frac{dr^2}{\left(1-\frac{|K|}{4}r^2\right)^2}=d\rho^2$で導入します。積分して
$$
\rho=\frac{1}{\sqrt{|K|}}\log\frac{\sqrt{|K|}r+2}{\sqrt{|K|}r-2}
$$
となるので
$$
r= \frac{2}{\sqrt{|K|} \tanh{\left(\frac{\sqrt{|K|} \rho}{2} \right)}}
$$
が得られ、
$$
\frac{r^2d\theta^2}{\left(1-\frac{|K|}{4}r^2\right)^2}=\frac{1}{|K|}\sinh^2(\sqrt{|K|}\rho)d\theta^2
$$
なので、
$$
\frac{dr^2+r^2d\theta^2}{\left(1-\frac{|K|}{4}r^2\right)^2}=d\rho^2+\frac{1}{|K|}\sinh^2(\sqrt{|K|}\rho)d\theta^2
$$
となります。また
$$
\frac{r^2d\theta}{1-\frac{|K|}{4}r^2}= - \frac{4 \cosh^{2}{\left(\frac{\sqrt{|K|} \rho}{2} \right)}}{|K|}= - \frac{4 \sinh^{2}{\left(\frac{\sqrt{|K|} \rho}{2} \right)}}{|K|}d\theta-\frac{4}{|K|}d\theta
$$
なので
$$
\begin{align}
ds^2&=-\left(dt+\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2}\right)^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}\\
&=-\left(dt+\frac{2\omega}{|K|} \sinh^{2}\left(\frac{\rho}{2} \right)d\theta\right)^2+\frac{1}{|K|}(d\rho^2+\sinh^2\rho d\theta^2)
\end{align}
$$
となります。ただし、$t-4/|K|\to t,\ \sqrt{|K|}\rho\to\rho$と置き直しました。$|K|=\omega^2/2$とすればGödel宇宙のHyperbolic model based座標
$$
ds^2=-\left(dt+\frac{4}{\omega} \sinh^{2}\left(\frac{\rho}{2} \right)d\theta\right)^2+\frac{2}{\omega^2}(d\rho^2+\sinh^2\rho d\theta^2)+dz^2
$$
が得られます。
Holocycle based座標とPoincare model based座標の関係
この2つの関係は少し複雑です。まずGödel宇宙のHolocycle based座標は
$$
ds^2=\frac{2}{\omega^2}\left(- (dt + e^{- x}dy)^2+dx^{2} + \frac{e^{- 2 x}}{2}dy^{2} +dz^2\right)
$$
で与えられます。この座標からPoincare model based座標への座標変換の幾何学的な仕組み解説します。本質的なのは
$$
ds^2=- (dt + e^{- x}dy)^2+dx^{2} + \frac{e^{- 2 x}}{2}dy^{2}
$$
の3次元時空の部分なのでここから考察を始めます。実は2次元リーマン多様体
$$
ds^2=dx^{2} + \frac{e^{- 2 x}}{2}dy^{2}
$$
は双曲平面のHolocycle座標と呼ばれる座標であり、この理由からHolocycle based座標と呼びました。座標変換
$$
e^x=\frac{\xi}{\sqrt{2}}
$$
により
$$
ds^2=\displaystyle - \left(dt + \frac{\sqrt{2} dy}{\xi}\right)^{2} + \frac{d\xi^{2} + dy^{2}}{\xi^{2}}
$$
となり、これで双曲平面の座標が上半平面モデルになりました。さらに上半平面$H$をポアンカレディスク$D_p$に写しましょう。
$z=y+i\xi\in H$と$w=\zeta+i\eta\in D_p,\ |w|<1$は
$$
z=-i\frac{w-1}{w+1}
$$
でつながります。すなわち変換
$$
\begin{align}
y&=\frac{2\eta}{\eta^2+(\zeta+1)^2},\\
\xi&=\frac{1-\eta^2-\zeta^2}{\eta^2+(\zeta+1)^2}
\end{align}
$$
により
$$
ds^2= - \left(dt + \frac{\sqrt{2} dy}{\xi}\right)^{2}+4\frac{d\eta^2+d\zeta^2}{(1-\eta^2-\zeta^2)^2}
$$
となります。$\frac{\sqrt{2} dy}{\xi}$も代入して計算すればいいのですが、よく考えると戦略的に計算できます。
まず初めの座標
$$
ds^2=- (dt + e^{- x}dy)^2+dx^{2} + \frac{e^{- 2 x}}{2}dy^{2}
$$
を思い出します。$d(dt + e^{- x}dy)=-e^xdx\wedge dy$は双曲平面の体積形式に比例しています。これは座標に依存しない性質ですから、今の座標$(t,\eta,\zeta)$においても$\frac{\sqrt{2} dy}{\xi}$の外微分は$4\frac{d\eta\wedge d\zeta}{(1-\eta^2-\zeta^2)^2}$に比例するはずです。
$$
d\left(\frac{\zeta d\eta-\eta d\zeta}{1-\zeta^2-\eta^2}\right)=2\frac{d\eta\wedge d\zeta}{(1-\eta^2-\zeta^2)^2}
$$
なので、$a\in\mathbb{R}$と関数$f$により
$$
\frac{\sqrt{2} dy}{\xi}=a\frac{\zeta d\eta-\eta d\zeta}{1-\zeta^2-\eta^2}+df
$$
と変形できるはずです。
$$
\begin{align}
\frac{\sqrt{2}dy}{\xi}&=2\sqrt{2}\frac{\zeta d\eta-\eta d\zeta}{1-\zeta^2-\eta^2}+df,\\
f&=\displaystyle - 2\sqrt{2} \operatorname{atan}{\left(\frac{\zeta}{\eta} + \frac{1}{\eta} \right)}
\end{align}
$$
を示せ。
このことから時間一定面のスライスを
$$
t=\tau-f
$$
と取り換えれば
$$
ds^2= - \left(d\tau + 2\sqrt{2}\frac{\zeta d\eta-\eta d\zeta}{1-\zeta^2-\eta^2}\right)^{2}+4\frac{d\eta^2+d\zeta^2}{(1-\eta^2-\zeta^2)^2}
$$
となります。よって
$$
ds^2=-\frac{\omega^2}{2}\left( (dt + e^{- x}dy)^2+dx^{2} + \frac{e^{- 2 x}}{2}dy^{2}\right)
$$
に今の変換を施して、さらに
$$
\tau=\frac{\sqrt{2}}{\omega}\tau',\ \eta=\frac{\omega}{2\sqrt{2}}\eta',\ \zeta=\frac{\omega}{2\sqrt{2}}\zeta'
$$
として、$\tau'$などを再び$\tau$などと書けば、
$$
ds^2= - \left(d\tau + \frac{\omega}{2}\frac{\zeta d\eta-\eta d\zeta}{1+K/4(\zeta^2+\eta^2)}\right)^{2}+\frac{d\eta^2+d\zeta^2}{(1+K/4(\eta^2+\zeta^2))^2},\ K=-\frac{\omega^2}{2}
$$
となります。$\eta,\zeta$を極座標で書けばPoincare model based座標が得られます。
3つの座標のまとめ
3つの座標について結果をまとめておきます。
Gödel宇宙の３つの座標により計量はそれぞれ次のように書かれる。
(i) Holocycle based座標
$$
ds^2=\frac{2}{\omega^2}\left(- (dt + e^{- x}dy)^2+dx^{2} + \frac{e^{- 2 x}}{2}dy^{2} +dz^2\right)
$$
(ii) Hyperbolic model based座標
$$
ds^2=-\left(dt+\frac{4}{\omega} \sinh^{2}\left(\frac{\rho}{2} \right)d\theta\right)^2+\frac{2}{\omega^2}(d\rho^2+\sinh^2\rho d\theta^2)+dz^2
$$
(iii) Poincare model based座標
$$
ds^2=-\left(dt+\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2}\right)^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}+dz^2,\ K=-\frac{\omega^2}{2}
$$
演習問題の解答
演習問題の解答です。
[問題１の解答]
$${}^\flat\partial_t=dt+\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2}(=:\eta)$$
であり
$$d\eta=\omega\frac{rdr\wedge d\theta}{(1+\frac{K}{4}r^2)^2}$$
である。$\frac{rdr\wedge d\theta}{(1+\frac{K}{4}r^2)^2}$が2次元双曲空間の体積形式であることに注意すると、
$||{\rm rot}(\partial_t)||^2=||d\eta||^2=\omega^2||\frac{rdr\wedge d\theta}{(1+\frac{K}{4}r^2)^2}||^2=\omega^2$
[問題２の解答]
$$
Ric-\frac{1}{2}Rg+\Lambda g=T
$$
の両辺の$Tr$を取れば、
$$
-R+4\Lambda=Tr(T)
$$
となるから、元の方程式に代入して
$$
Ric=T-\frac{1}{2}Tr(T)g+\Lambda g
$$
となる。
[問題３の解答]
$\xi$は適当に規格化して$||\xi||^2=\pm1$であるとしてよい。$U$を任意の開近傍とする。$U$上の正規直交フレーム$\{\xi,e_1,\cdots,e_n\}$を取る。
$$
\begin{align}
g(\nabla_\xi\xi,\xi)&=\frac{1}{2}\xi(||\xi||^2)=0,\\
g(\nabla_\xi\xi,e_i)&=-g(\nabla_{e_i}\xi,\xi)=-\frac{1}{2}e_i(||\xi||^2)=0,
\end{align}
$$
であるから、$\nabla_\xi\xi=0$である。
[問題４の解答]
$\{e_1,e_2\}$を正規直交フレームとする。
$$
\begin{align}
\Omega_2(e_1,e_1)&=\Omega(e_1,e_1)^2+\Omega(e_1,e_2)^2=1,\\
\Omega_2(e_1,e_2)&=\Omega(e_1,e_1)\Omega(e_2,e_1)+\Omega(e_1,e_2)\Omega(e_2,e_2)=0,\\
\Omega_2(e_2,e_2)&=\Omega(e_2,e_1)^2+\Omega(e_2,e_2)^2=1
\end{align}
$$
より$\Omega_2=g$である。
また局所座標表示すれば$\Omega=\sqrt{\det g}dx^1\wedge dx^2$であるから、$\nabla g=0$であることから$\nabla_i\Omega_{jk}=0$である。よって$div\Omega=\nabla^i\Omega_{ij}=0$である。
[問題５の解答]
$$
\frac{dy}{\xi}-2\frac{\zeta d\eta-\eta d\zeta}{1-\zeta^2-\eta^2}= \frac{2 \left(\zeta + 1\right)}{\eta^{2} + \zeta^{2} + 2 \zeta + 1}d\eta\displaystyle - \frac{2 \eta}{\eta^{2} + \zeta^{2} + 2 \zeta + 1}d\zeta
$$
であり、
$$
\int \left(- \frac{2 \eta}{\eta^{2} + \zeta^{2} + 2 \zeta + 1}\right)d\zeta= - 2 \operatorname{atan}{\left(\frac{\zeta}{\eta} + \frac{1}{\eta} \right)}
$$
より
$$
\frac{dy}{\xi}-2\frac{\zeta d\eta-\eta d\zeta}{1-\zeta^2-\eta^2}=d\left(- 2 \operatorname{atan}{\left(\frac{\zeta}{\eta} + \frac{1}{\eta} \right)}\right)
$$
を得る。
参考文献についての少しの説明
参考文献について簡単に説明します。
文献[1]（井ノ口順一, はじめて学ぶリー群 ―線型代数から始めよう）には3次元Lie群に左不変計量を入れることでThurstonのモデル空間またはBianchi分類として知られる空間達が紹介され、そしてこれらの空間達は計量に2つのパラメータを持つBianchi-Cartan-Vranceanu空間族として統一的に記述されることが解説されています。これらのことを勉強するのにコンパクトでよい文献だと思います。
文献[2]（佐藤 文隆, 小玉 英雄, 一般相対性理論）では時空の対称性の観点からEinstein方程式の厳密解が紹介されています。Gödel宇宙は5次元の実Lie群が作用する時空的に一様な4次元時空という位置づけになります。Gödel宇宙についてHolocycle based座標での計量、完全流体を物質とする宇宙項無しのEinstein系の厳密解であること、時間的閉曲線の存在が非常にコンパクトに解説されています。
文献[3]（S.W.Hawking, G.F.R.Ellis, The Large Scale Structure of Space-Time）ではdust流体($P=0$)を物質とする宇宙項を持つEinstein系の厳密解としてGödel宇宙が導入されています。Holocycle based座標で計量が与えられ、Hyperbolic model based座標への座標変換が結果だけ与えられています。また時間的閉曲線やnull測地線のcausticなどの因果構造についても解説があります。
文献[4]（M.GURSES, M.PLAUE, AND M.SCHERFNER, On a particular type of product manifolds and shear-free cosmological models）は
https://www.researchgate.net/publication/232279222_On_a_particular_type_of_product_manifolds_and_shear-free_cosmological_models
からもアクセスできます。このノートではノルムが一定のtimelike Killingベクトル場に関するRicciテンソルの分解公式を使いましたが、一般のノルム一定のtimelikeベクトル場に関する状況での$1+n$分解の公式が与えられています。計算はかなり大変です。
