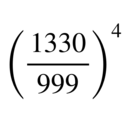4/πに収束する級数（有名なアレではないです…。）

円周率の逆数に収束する級数といえばラマヌジャンの複雑かつ高速な式が有名ですが、ここではもっと単純（その代わりに収束も遅いけど）な式を紹介したいと思います。

$$ \frac{1}{\sqrt{1-x}}=\sum_{n=0}^\infty\frac{(2n-1)!!}{(2n)!!}x^n $$
両辺を$0$から$x$まで積分して、
$$ 2(1-\sqrt{1-x})=\sum_{n=0}^\infty\frac{(2n-1)!!}{(n+1)(2n)!!}x^{n+1} $$
両辺を$x$で割って
$$ 2\cdot\frac{1-\sqrt{1-x}}{x}=\sum_{n=0}^\infty\frac{(2n-1)!!}{(n+1)(2n)!!}x^n $$
$x$に$\sin^2{\theta}\left(0\lt\theta\leqq\frac\pi2\right)$を突っ込んで
$$ 2\cdot\frac{1-\cos{\theta}}{\sin^2{\theta}}=\sum_{n=0}^\infty\frac{(2n-1)!!}{(n+1)(2n)!!}\sin^{2n}{\theta} $$
ここで両辺を$0$から$\frac\pi2$まで積分するのですが、
$$\begin{split} \int_{0}^{\frac\pi2}\frac{1-\cos{\theta}}{\sin^2{\theta}}&=\left[-\frac1{\tan{\theta}}+\frac1{\sin{\theta}}\right]_0^\frac\pi2\\&=\left[\frac{1-\cos{\theta}}{\sin{\theta}}\right]_0^\frac\pi2\\&=\left[\frac{\sin\theta}{1+\cos\theta}\right]_0^\frac\pi2\\&=1 \end{split}$$
であり、またウォリス積分$ \int_{0}^{\frac\pi2}\sin^{2n}{\theta}=\frac{(2n-1)!!}{(2n)!!}\cdot\frac\pi2 $から
$$ 2=\frac\pi2\sum_{n=0}^{\infty}\frac{1}{n+1}\left\{\frac{(2n-1)!!}{(2n)!!}\right\}^2 $$
よって
$$ \frac{4}{\pi}=\sum_{n=0}^\infty\frac{1}{n+1}\left\{\frac{(2n-1)!!}{(2n)!!}\right\}^2 $$
を得ました。

雑記

多分これも楕円に関係してるんでしょーね。楕円関数をマトモに勉強したことがないので知りませんけど。そもそも今までマトモに勉強したものってあったっけ…。関係ないですけどアイゼンシュタイン級数が面白いです。