相対位相って何
どうも
こんにちは 夏休みが終わり絶望しているごておばけです
位相空間論初見のとき、相対位相の定義を見ても何もピンとこなかった経験があるので 過去の自分向けに相対位相の具体的な使い方を説明しようと思います
$\mathbb{R}^n$での開集合とはなんだったか
基礎的な2変数以上の解析学を学ぶとき、まず$\mathbb{R}^2$における開集合と閉集合の定義を知ることになると思います（僕がそうだっただけでそうでないかもしれませんが......）
折角（？）なので開集合の定義をしましょう
$x \in \mathbb{R}^n,$$\epsilon>0$に対して, $N_{\epsilon}(x)=\{$$y\in \mathbb{R}^n$$|$$d(x,y) < \epsilon$$\}$と定める.（ただし, $d(x,y)$は$x,y$の間のユークリッド距離を表す.）
$A \subset \mathbb{R}^n$とする. 任意の点$x \in A$に対して$N_{\epsilon}(x) \subset A$となるような$\epsilon>0$がとれるとき, $A$は開集合であるという.
開集合のイメージも書いておきます
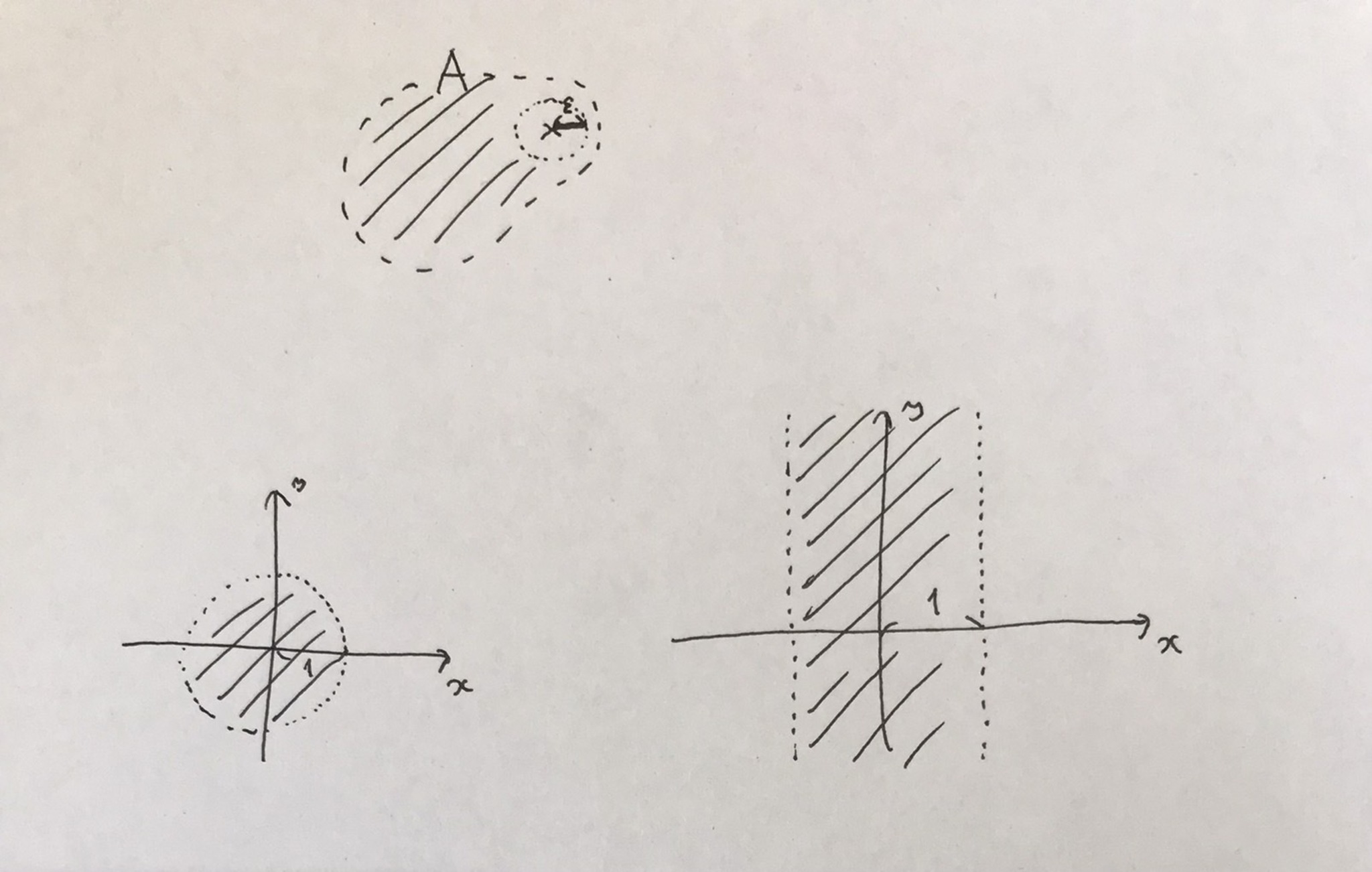手書き
画像のように, 「境界がない図形」「果てがない図形」という感じのものが開集合です.
球面における開集合を定義したい！
さて, 我々は地表に住んでいるので球面というものに自然と興味が湧いてきます 湧きますよね？
球面を次で定義します.
2次元球面$S^2 \subset \mathbb{R}^3$を$S^2=\{$$x \in \mathbb{R}^3$$|$$d(x,O)=1$$\}$で定める.（ただし, $d(x,y)$は$x,y$の間のユークリッド距離を表し, $O$は原点を指す. ）
さて, これを幾何学的な対象と見たいので球面における開集合を考えてみましょう. （位相空間にしましょう. ）
球面における「境界がない図形」「果てがない図形」とはどういう図形になるか. 次の画像のようなものが思い浮かぶと思います.
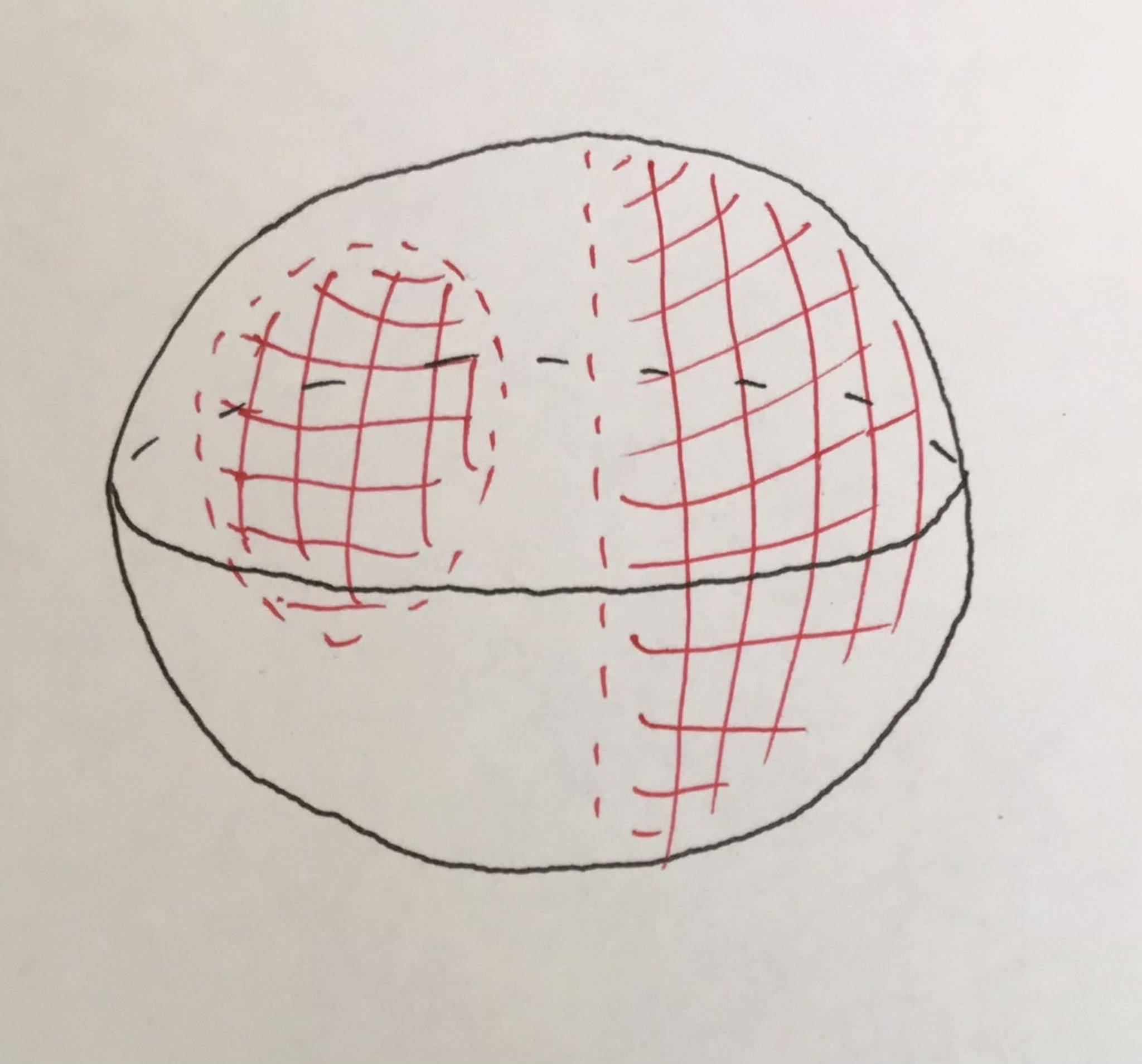なんか不安になる図
球の表面にペタっと開集合がくっついている感じですね. さてこの領域ですが, これをうまく数学的に定義したい！という気持ちになります.
超簡単な解決策
では, 球面における開集合を定義してみます.
$B \subset S^2$とする. $\mathbb{R}^3$の開集合$O$があり$B = S^2 \cap O$とかけるとき, $B$は$S^2$の開集合であるとする.
例えば図2の右側の開集合は, $S^2$と$\{$$(a_1,a_2,a_3) \in \mathbb{R}^3$$|$$a_1>0$$\} \subset \mathbb{R}^3$の共通部分として考えることができます.
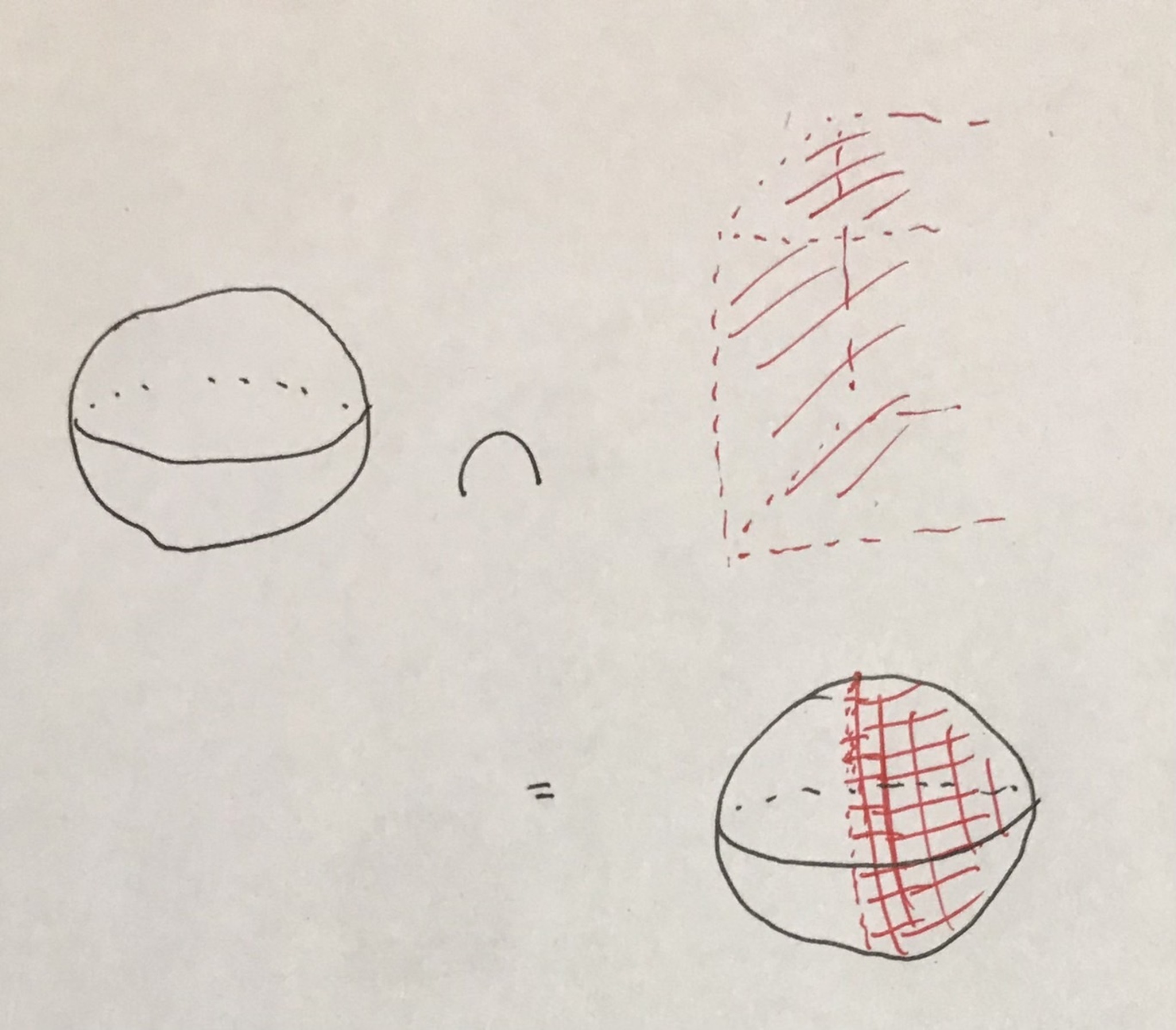イメージ図
左側の開集合も, いい感じに開集合を作ると実現できそうです.（想像してみてください......）こうして, ユークリッド空間の開集合というお手本から簡単に開集合を定義することができました.
開集合系（開集合をすべて集めてきたもの）の観点で見てみましょう. 球面の開集合系は, 次のような形で書くことができます.
$\mathcal{O}=\{ $$ S^2 \cap O $$ | $$ O $は$\mathbb{R^3}$の開集合$\}$
相対位相を定義しよう
位相空間の定義を貼っておきます.
$X$を空でない集合, $\mathcal{O}$を$X$の部分集合を元とする集合（$X$の冪集合$2^X,P(X)$の部分集合のこと）について, 次の$(1)$-$(3)$が成立するとき, $X$,また組$(X,\mathcal{O})$を位相空間とよび, $\mathcal{O}$の元を開集合, $X$の元を点とよぶ.
$(1)$ $X,\emptyset \in \mathcal{O}.$
$(2)$ $O_1 , O_2 \in \mathcal{O}$ とするとき, $O_1 \cap O_2 \in \mathcal{O}.$
$(3)$ $\{ O_{\lambda} \}_{\lambda \in \Lambda}$ を$\Lambda$を添え字とする$\mathcal{O}$の元の族とするとき,
$$
\hspace{15pt} \bigcup_{\lambda \in \Lambda} O_{\lambda} \in \mathcal{O}.
$$
さて, $(X,\mathcal{O})$を位相空間, $A \subset X$（$A$は空でない）とするときの相対位相を定義します.
$\mathcal{O}_A=\{ $$ A \cap O $$ | $$ O \in \mathcal{O} $$\}$ を$A$の上の$\mathcal{O}$に関する相対位相といい, $(A,\mathcal{O}_A)$を$(X,\mathcal{O})$の部分空間という.
上で定義した球面における開集合系は, $S^2$にユークリッド空間の位相を使って相対位相を考えたものに他なりません！
まとめ
相対位相の定義だけを見るとあっさりしていますが, 球面における開集合のように, すでにある位相空間を使っていい感じの位相空間が定まるという意味で相対位相は便利ですね. それではまた～～～