記事 2 回目です．
[Vec の記事 (Miquel の 6 円定理)](https://mathlog.info/articles/3405) に紹介されている二つ目の定理を，反転を使わずに示せたので書きました．短いです．



&&&thm 
以下の図で $4$ つの接点 $P,Q,R,S$ は共円．

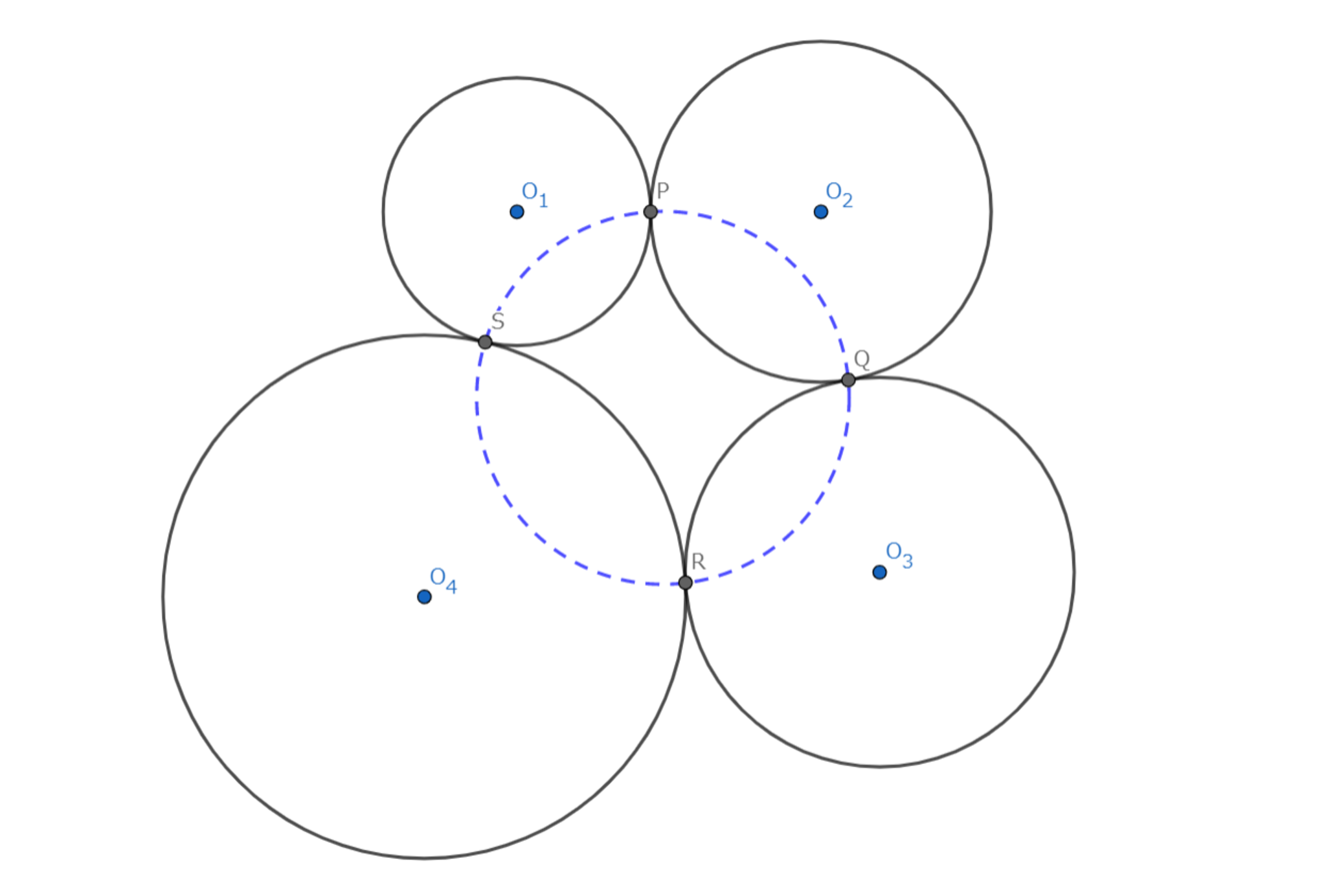![主張](/uploads/mathdown/20221001223051.png)
&&&


&&&prf 
　下図において赤，青，緑，橙色がついた角の和が $180^\circ$ であることを示せばよい（同じ印がついた角の大きさは接弦定理より等しい）．$4$ 円が接していることから $P$ は $O_1O_2$ 上にあり，他も同様．よって内角の和から $\angle SO_1P+\angle PO_2Q + \angle QO_3R + \angle RO_4S=360^\circ$ であり，円周角の定理より色のついた角の和はこれのちょうど半分であるから，結論を得る．
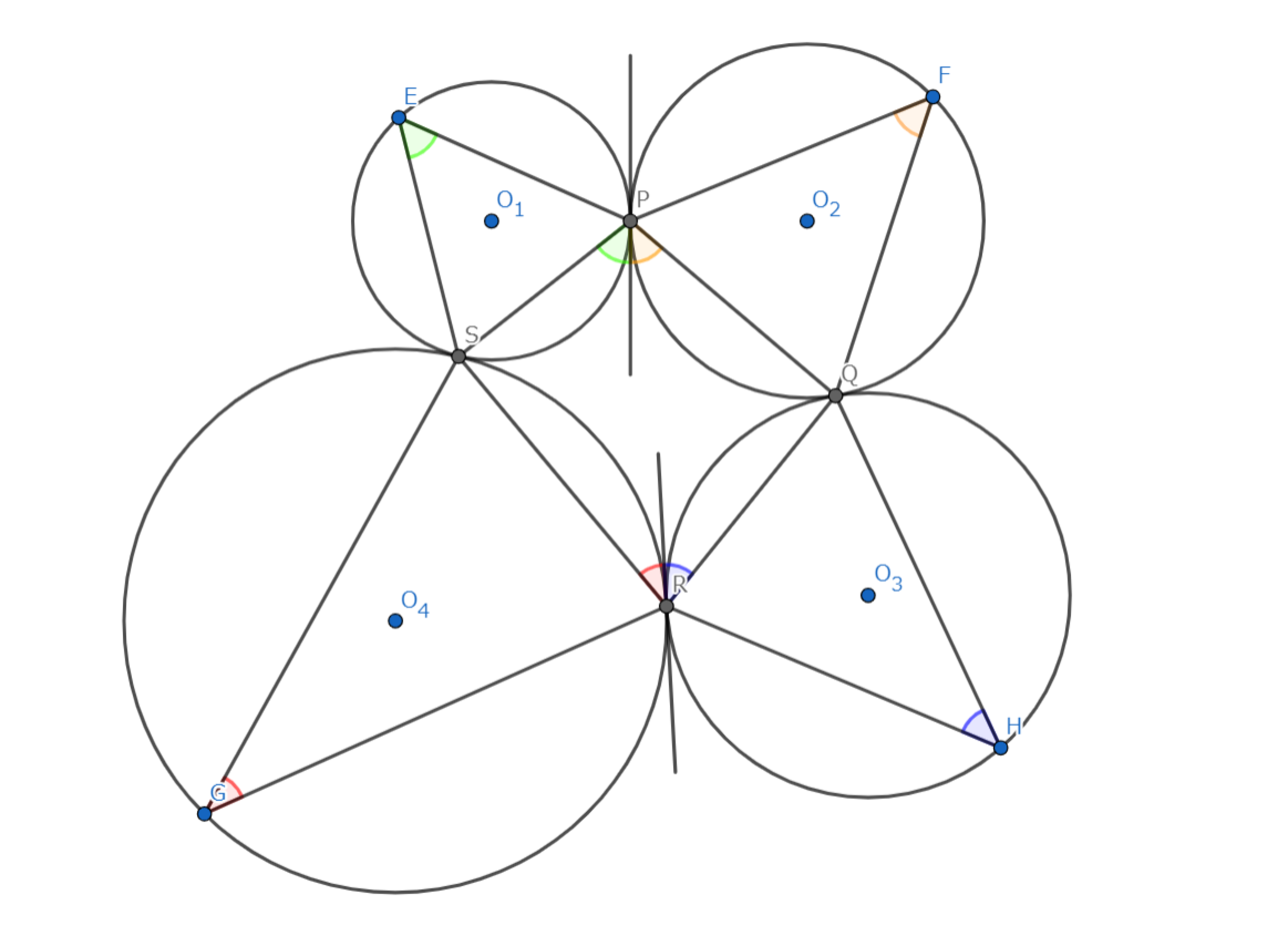![色がきれい](/uploads/mathdown/20221001225739.png)
&&&


４円が接する構図の話

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント