文献あり

極で反転

480

2022/11/3 14時ごろ　「$Q$は$\triangle OPP^\prime$の垂心」に気付いたので追加
2022/11/3 21:44　「定理1」における誤字の修正 (lockerさんより)
2023/3/27 21:54　参考文献のスペルミスを修正（"Mathmatical"$\rightarrow$"Mathematical"）

極の性質

EGMO9章の序盤を読んで、極と極線の性質を初等幾何で示すのは勿体無いと思ったので、反転と射影幾何で証明します。

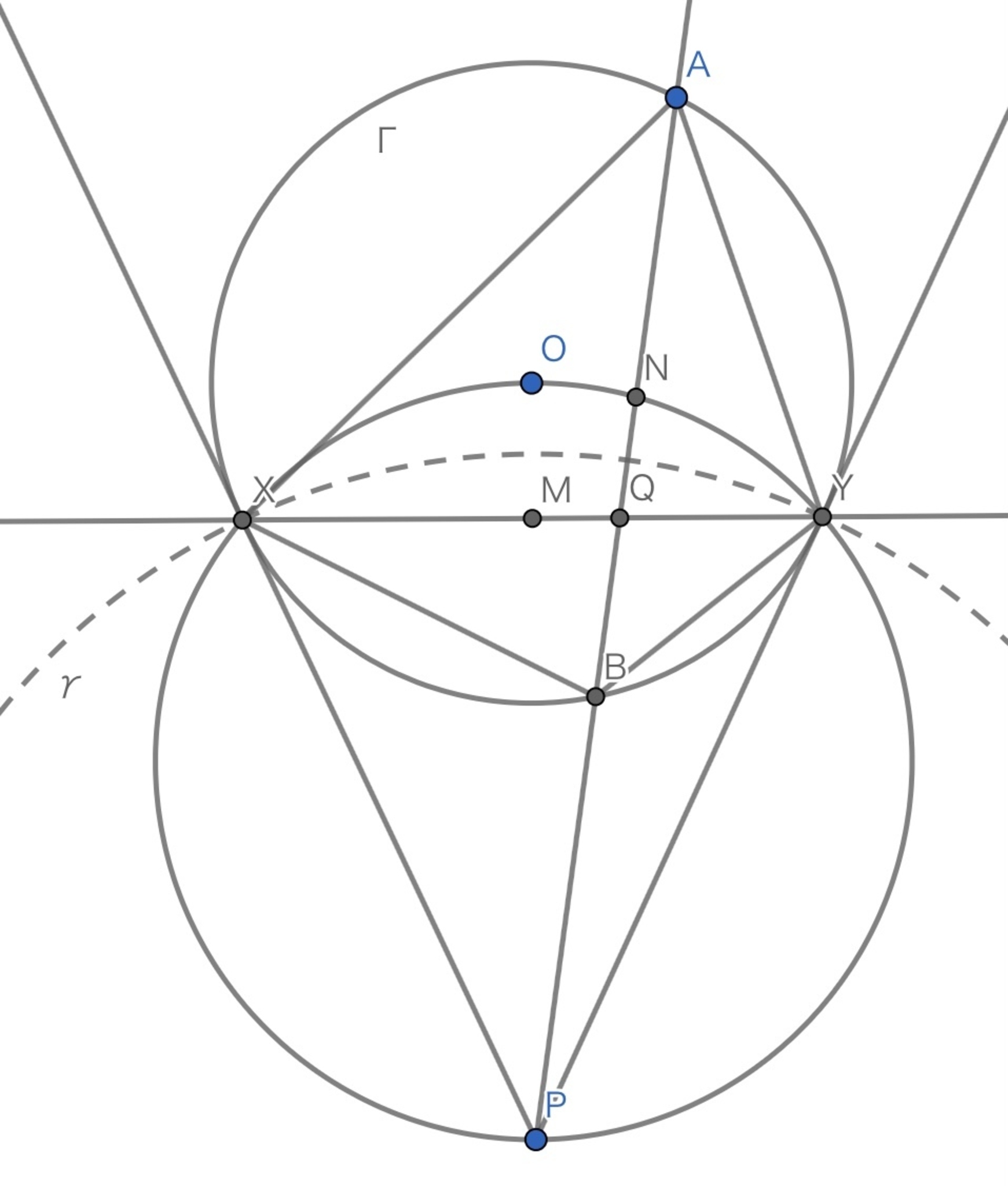
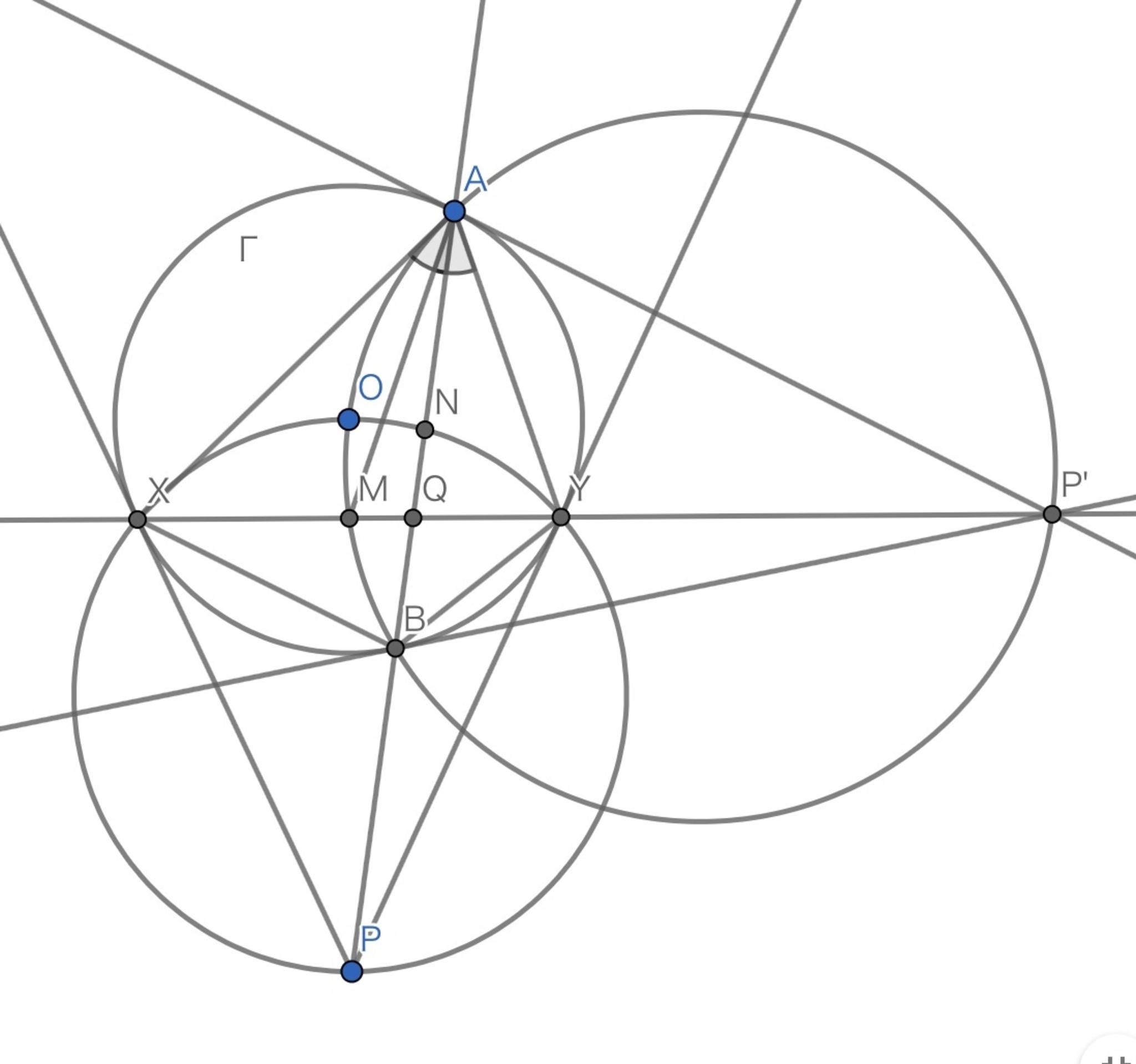
円$\Gamma$とその外点$P$をとり、$P$の極線と$\Gamma$の交点を$X,Y$とする。$P$を通り、$\Gamma$上の$2$点$A,B$を通る直線と直線$XY$の交点を$Q$とおくと、$A,Q,B,P$は調和点列である。

調和点列

$\Gamma$の中心を$O$、線分$AB$の中点を$N$とおくと，
$$\angle ONP = 90^\circ = \angle OXP = \angle OYP$$
より，$5$点$O,N,P,X,Y$は共円。
中心$P$、半径$PX$の円(図の円$\gamma$)で反転する。
このとき，$X,Y$は不変であり、$PA \cdot PB = PX^2$より、$A$は$B$に、$B$は$A$にうつる。(オマケ:$\Gamma$も不変)
したがって、$O,N,P,X,Y$の外接円は直線$XY$にうつるから、$N$は$Q$にうつる。
ここで、$(A,B;N,P_\infty) = -1$より，反転された$(B,A;Q,P)$も$-1$であるから、$A,Q,B,P$は調和点列である。(ただし、$P_\infty$は無限遠点)

定理1における$A,Y,B,X$は調和四角形を成す。

点や円の名前は今後も使いまわすので、「定理1における」とかは省略します。

点$X$を中心とする、直線$AP$から$\Gamma$への配景写像を$A,Q,B,P$に作用させると、これらは$A,Y,B,X$にうつる。
この写像は複比を保つので、$AYBX$は調和四角形。

これにより共役定理が示されます。

共役定理

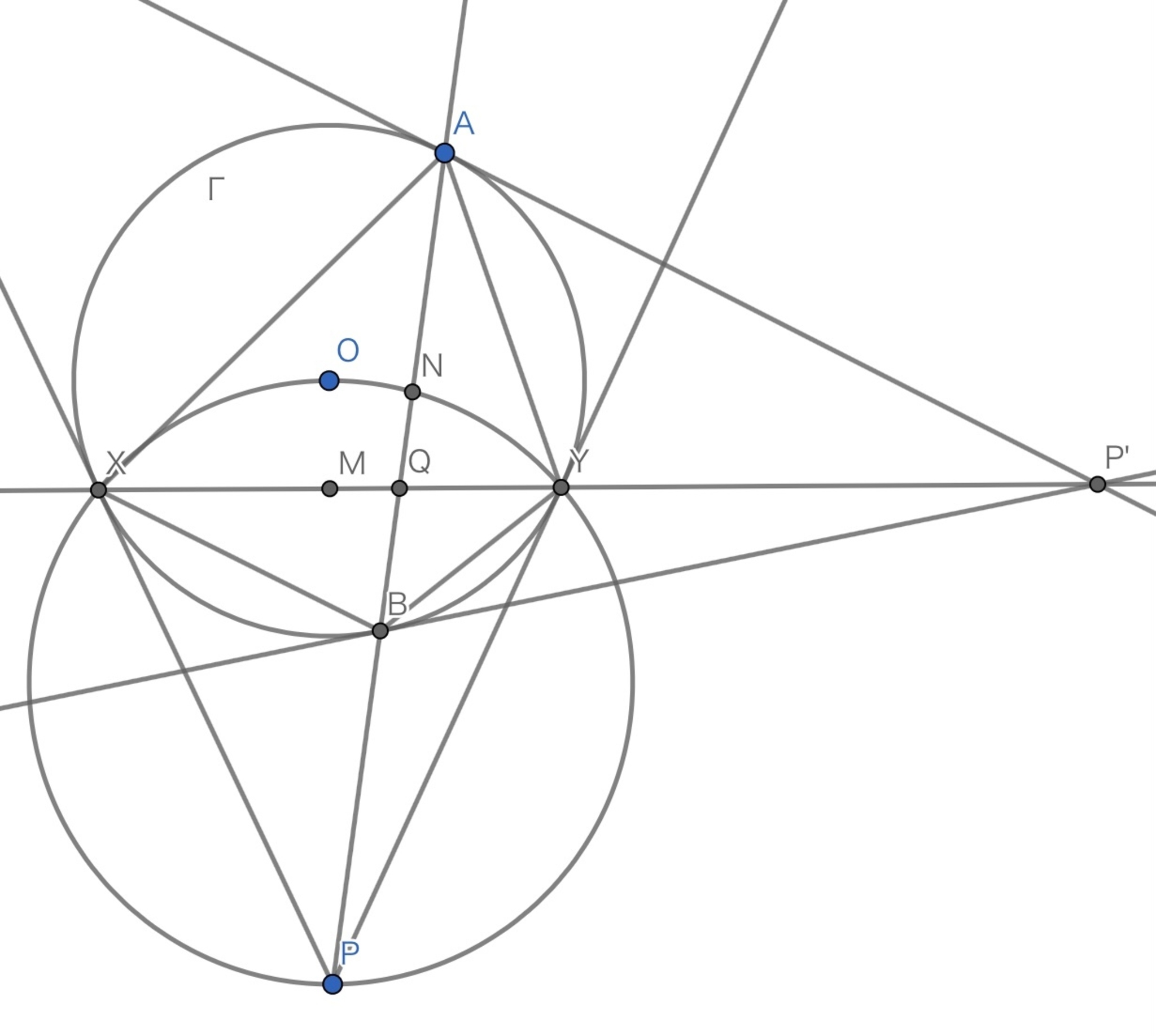
$AB$に対する極$P^\prime$は直線$XY$上に存在する。

共役定理

$A$を中心とする、$\Gamma$から直線$XY$への配景写像により，点$A$が点$P_1$にうつったとすると、$AP_1$は$\Gamma$に接し、さらに補題2より$X,Q,Y,P_1$は調和点列。
$B$を中心とする、$\Gamma$から直線$XY$への配景写像により、点$B$が点$P_2$にうつったとすると、$BP_2$は$\Gamma$に接し、さらに補題2より$X,Q,Y,P_2$は調和点列。
したがって$P_1=P_2$で、これは$AB$に対する極$P^\prime$である。

先ほどの反転と組み合わせると、こんな定理が生えます。

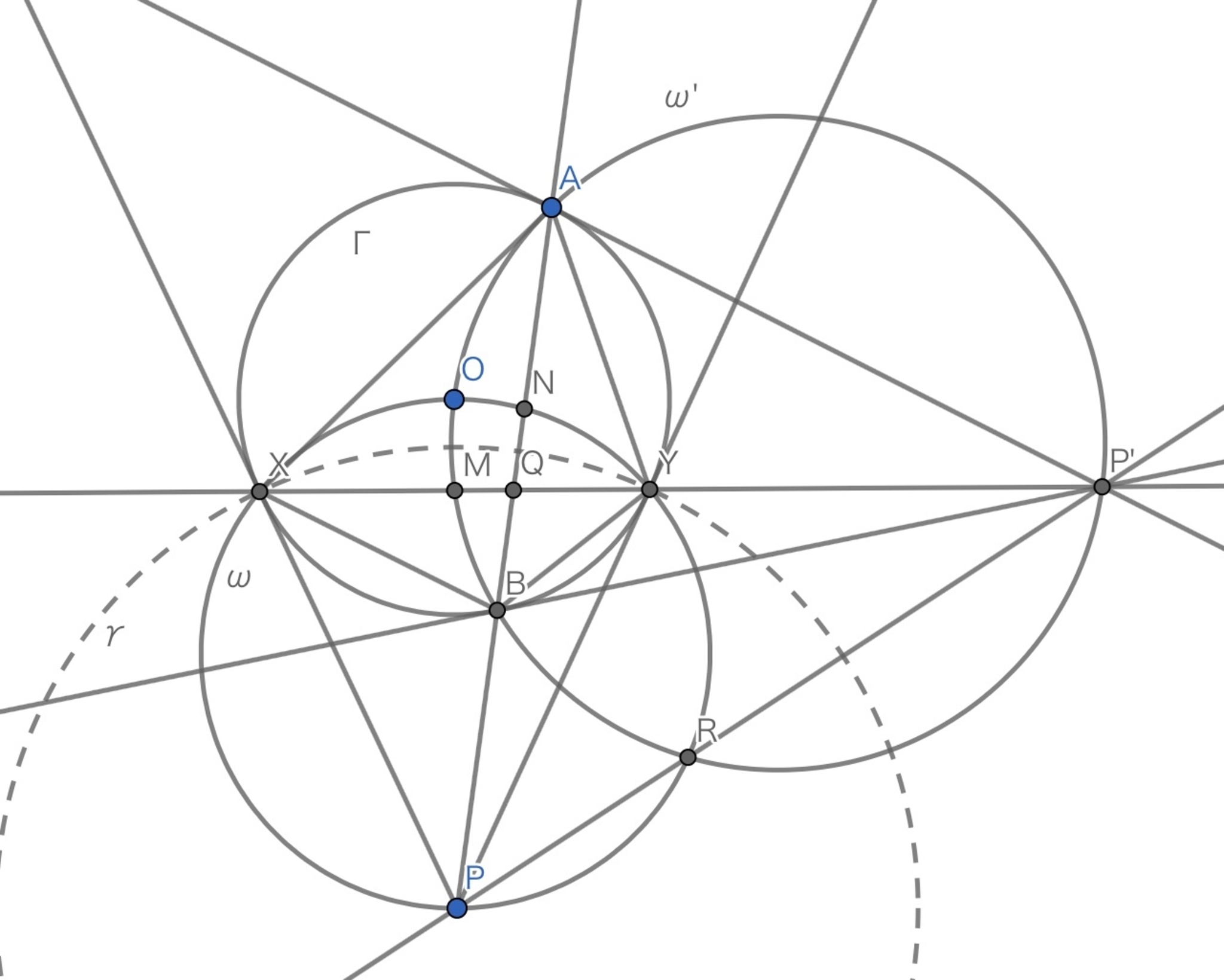
以下の$3$つの図形は共通の点$R$を通る。

点$P,X,Y(,O,N)$の外接円$\omega$
点$P^\prime,A,B(,O,M)$の外接円$\omega^\prime$
直線$PP^\prime$

定理4の図

円$\gamma$で反転する。
このとき、$\omega$は直線$XY$にうつるのであった。
$O,M,P$は共線であるから、反転で$O$は$M$に、$M$は$O$にうつる。
$A$は$B$に、$B$は$A$にうつるから、結局、$A,B,M,O$の外接円$\omega^\prime$は不変。
$P^\prime$の反転を$R^\prime$とおく。
点$P^\prime$は円$\omega^\prime$と直線$XY$の交点であるから、$R^\prime$は$\omega^\prime$と$\omega$の交点で、さらに直線$PP^\prime$上に存在する。

まだまだ性質は出てきます。

$Q$は$\Gamma,\omega,\omega^\prime$の根心。

命題 5

$O,Q,R$は共線。

系の反転

$M,N,P,P^\prime$は共円。

(実は、これら$3$つの命題は$1$つの定理に圧縮できます。)

$Q$は$\triangle OPP^\prime$の垂心。

$\angle ORP = 90^\circ,PN \perp OP, P^\prime M \perp OP$

$OR$は$MNPP^\prime$の外接円と$\gamma$の根軸。

$AMBR,XNYR$は調和四角形。

配景写像

調和点列$A,Q,B,P$を$P^\prime$中心の配景写像で$\omega^\prime$にうつすと、四角形$AMBR$にうつる。
$XNYR$についても同様。

反転

調和四角形$AOBP^\prime$を$\gamma$で反転したものが四角形$AMBR$である。
対称性より、$XNYR$も調和四角形。
なお、$XNYR$については、調和点列$XQYP^\prime$の反転と考えてもよい。

symmedian

極と極線といえばsymmedianです。
やっぱりsymmedianの性質は射影幾何ルートで示す方が嬉しいですよね？
ということで示します。
Metachickさんの記事での証明を共役定理で短縮しました。

直線$AP$は$\triangle AXY$の$A$-symedianである。

symmedianと共役定理

$A,O,M,P^\prime$は共円であるから，
$$\angle AXB = \angle AOP^\prime = \angle AMP^\prime = \angle AMY$$
$A,X,Y,B$は共円であるから，
$$\angle XBA = \angle XYA = \angle MYA$$
よって、$\triangle AXB \backsim \triangle AMY$であるから、$\angle YAM = \angle BAX = \angle PAX$
したがって、$AP$は$\triangle AXY$の$A$-symmedianである。

対称性を利用するとこの定理は$4$つに増えます。

直線$BP$は$\triangle BXY$の$B$-symmedianである。
直線$XP^\prime$は$\triangle XAB$の$X$-symmedianである。
直線$YP^\prime$は$\triangle YAB$の$Y$-symmedianである。

補遺

実は、定理1より先に補題2を示せば、反転なしで定理1を示せます。

補題 2

$\triangle PXA \backsim \triangle PBX,\triangle PYA \backsim \triangle PBY$より、
$\left| \dfrac{XA}{XB} \right| = \left| \dfrac{PA}{PX} \right| = \left| \dfrac{YA}{YB} \right|$, $\left| (A,B;X,Y) \right|=1$
$4$点の位置関係より、複比は負であるから、$A,B,X,Y$は調和四角形。

定理 1

定理 1$\Rightarrow$補題 2を示すときに使った配景写像の逆写像を取ればよい。