底辺1・高さ2の直角三角形の角度を計算しよう〈中学受験生向け〉
久々の更新。今回は普段より易しめ、かつ短めの記事である。小学生(中学受験算数レベルの知識があるとよい)にも読まれることを想定し、小学校で習わない漢字・読みにはふりがなを付けている。
問題
下の問題について考えよう。なお、$\theta$はギリシャ文字の1つで、「シータ」と読む。
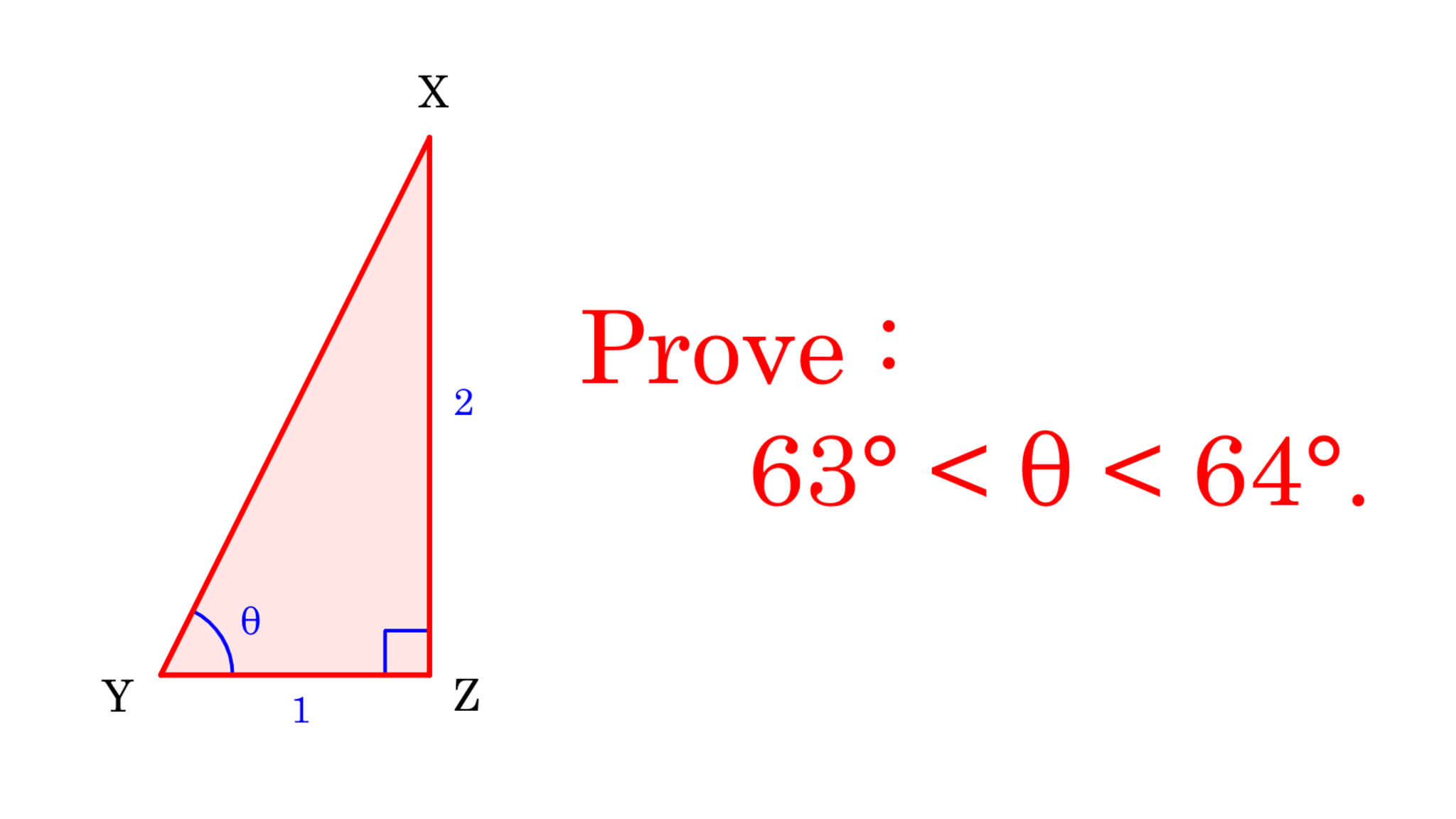
解説
最初に、「三角形$XYZ$」を「$\triangle XYZ$」、「角$X$」を「$\angle X$」のように表す旨をことわっておく。
準備

まずは、$3:4:5$の直角三角形を描いてみる(この三角形が直角三角形となることは中学受験算数の常識である)。
$AB=5,$$BC=4,$$AC=3$である直角三角形$ABC$を用意して、$\angle A$の二等分線と$BC$が交わる点を$D$とする。同様に、$\angle B$の二等分線と$AC$が交わる点を$E$とする。
すると、$AD$は$\angle A$の二等分線なので、$AB:AC=BD:DC$となる(この性質も最近は有名である)。
$BD+DC=BC=4$を用いて$DC$の長さを求めると、
$$\begin{align*}
AB:AC&=(BC-DC):DC \\
5:3&=(4-DC):DC \\
5\times DC&=3\times (4-DC) \\
5\times DC&=12 - 3\times DC \\
8\times DC&=12 \\
DC&=\dfrac{3}{2}
\end{align*}$$である(ここからは、こういった計算の多くを省略する)。同様にして、$CE=\dfrac{4}{3}$も分かる。
いま、$DC:AC=\dfrac{3}{2}:3=1:2$であるから、$\triangle ADC$と$\triangle XYZ$は相似の関係にある。つまり、$\angle ADC=\angle Y=\theta$が成り立っている。
$\theta$を利用して$\angle DAC,$$\angle EBC$の大きさを計算すると、
$$\angle DAC={90}^{\circ}-\theta,\,\angle EBC=\theta -{45}^{\circ}$$が得られる。
以降、$\triangle ADC$と$\triangle BEC$に注目していく。
$\theta > {63}^{\circ}$を示す

$\triangle BEC$を$9$倍に拡大し、$\triangle FGH$を作る。$\angle GFH$$=\angle GFK$$=\angle KFI$$=\angle HFL$$=\angle LFJ$をみたすように、上の図を参考にして直線$GH$上の4点$I,J,K,L$をとる。
相似比から$FH=36,$$GH=12$である。また、角度に注目すると$\triangle ABC$と$\triangle KFH$の相似が分かるので、
$$\begin{align*}
&KG=KH-GH=FH\times \dfrac{AC}{BC}-GH=36\times \dfrac{3}{4}-12=15 \\
&FJ=FK=FH \times \dfrac{AB}{BC}=36 \times \dfrac{5}{4}=45
\end{align*}$$となる。
$G$と$L$、$K$と$J$は点$H$に関してそれぞれ対称な位置にあり、$HL=12,$$LJ=15$が分かる。
ここで$IK$の長さを求めよう。$FK$が$\angle IFG$の、$FG$が$\angle IFL$の、それぞれ二等分線となっているから、
$$\begin{align*}
FI:FG&=IK:KG=IK:15 \\
FI:FL&=IG:GL=(IK+15):24
\end{align*}$$である。いま、$FG=FL$が簡単に分かるので、
$$\begin{align*}
IK:15&=(IK+15):24
\end{align*}$$となって、結局$IK=25$が導かれる。
$IJ$の長さは
$$IJ=25+15+12+12+15=79$$なので、辺$IJ$上に$MJ=75$となる点$M$をとることができる。$\triangle ABC$と$\triangle JMF$に注目すると、
$$\begin{align*}
&JM:JF=75:45=5:3 \\
&\angle MJF=\angle FKH=\angle BAC
\end{align*}$$より、この2つは相似である。つまり、
$$\begin{align*}
\angle MFJ&=\angle BCA={90}^{\circ} \\
\angle IFJ&=\angle IFM+\angle MFJ=\angle IFM+{90}^{\circ}
\end{align*}$$から、$\angle IFJ>{90}^{\circ}$を得る。したがって、
$$\begin{align*}
\angle IFJ&=\angle GFH \times 5=\angle EBC \times 5=\theta \times 5 -{225}^{\circ} \\
{90}^{\circ}&<\theta \times 5 -{225}^{\circ} \\
\end{align*}$$という式を立てられて、$\theta > {63}^{\circ}$を証明できる。やっと半分である。
$\theta < {64}^{\circ}$を示す

$\triangle ADC$を$10$倍に拡大し、$\triangle NOP$を作る。$\angle ONP$$=\angle ONQ$$=\angle PNS$$=\angle SNR$をみたすように、上の図を参考にして直線$OP$上の3点$Q,R,S$をとる。
相似比から$QP=RP=40,$$NQ=NR=50$である。また、角度に注目すると$\triangle ABC$と$\triangle NQP$の相似が分かるので、
$$\angle QNR=\angle ONP \times 4=\angle DAC \times 4={360}^{\circ}-\theta \times 4$$といえる。
さて、直線$NQ$上に$\angle QTR={90}^{\circ}$をみたす点$T$をとる。角度に注目すると$\triangle ABC$と$\triangle RQT$の相似が分かるので、
$$\begin{align*}
&NT=QT-QN=QR\times \dfrac{BC}{AB}-QN=80\times \dfrac{4}{5}-50=14 \\
&RT=QR \times \dfrac{AC}{AB}=80 \times \dfrac{3}{5}=48 \\
&\angle NRT=\angle QNR-\angle NTR={270}^{\circ}-\theta \times 4
\end{align*}$$となる。ゆえに、$\triangle NTR$の面積は$\dfrac{14\times 48}{2}=$$336$である。
点$T$に関して$N$と対称な位置にある点を$U$とし、直線$RU$に関して$N$と対称な位置にある点を$V$とする(図を参考にすること)。
四角形$NUVR$の面積を$\bigstar$とし、$NV$の長さを求めよう。
いま、$UR=NR$であり、$NV$と$UR$は垂直に交わっているので、
$$\bigstar = \dfrac{NV \times UR}{2}=NV \times \dfrac{NR}{2}=NV \times 25$$が成立する。
一方で、四角形$NUVR$の面積は明らかに$\triangle NTR$の面積の$4$倍であるから、
$$\bigstar = 336 \times 4 = 1344$$と求められる。これらを用いると、
$$NV \times 25 = 1344$$
となって、結局$NV=53.76$が導かれる。
いよいよ仕上げである。$\triangle NVR$の各辺の長さは
$$RN=RV=50,\,NV=53.76$$
であるから、1辺の長さが$53.76$の正三角形と比較することで、$\angle NRV>{60}^{\circ}$と判明する。したがって、
$$\begin{align*}
\angle NRV&=\angle NRT \times 4={1080}^{\circ} - \theta \times 16 \\
{60}^{\circ}&<{1080}^{\circ} - \theta \times 16 \\
\end{align*}$$という式を立てられて、$\theta < {63.75}^{\circ} < {64}^{\circ}$を証明できる。
あとがき
この記事で紹介した証明方法は、
ポテト一郎
(
Twitter
)氏との共同研究で見つけたものである。
2019年の6月半ばに、筆者である
匿(Tock)
(
Twitter
)が本問を持ちかけた。それぞれで解法を用意し、お互いの解法を改良しあって、同月下旬に完成したのが上の証明、ということになる。
2人ともかなりの算数愛好家で、それゆえに議論も熱のこもったものとなった。この場を借りて、有意義なやりとりをしてくださったポテト一郎氏への感謝を申し上げる。あと記事の完成が遅れてしまってすみませんでした。今後は再発防止に努める所存です。
