角の三等分の幾何学

はじめに

AMC11日目．毎日ユニークで面白い記事に楽しませていただいている．今日は私，るさがモーリーの定理という定理について書いていこうと思う．
　私のことを知っている人ならば，私のことを組み合わせの人と認識しているかもしれないが，実は私は幾何好きである（解けるとは言っていない．残念ながら）．そこで学校での探究の時間で幾何の研究をし（といってもほとんど調べ学習レベルであるが），昨年のクリスマスに「数学が恋人！！！」と叫びながら研究発表をすることになった．それ以来その研究は誰の目に止まることもなく今日に至るわけであるが，そこで出会った美しさをこれで終わりにするというのはなんとももったいないと思い，今日この場で推し定理の布教，もとい紹介をさせていただく．
　テーマは先に述べた通り「フランク・モーリーの定理」．数学好きからすればもはやクリシェかもしれない．しかし，この定理の先には本来の主張に止まらない世界が広がっているのである．少々難しいところがあるかもしれないが，あまり気を張らずに美しさをのんびりと感じてもらえれば良い．
　各所に載せた図はあまりに複雑であり，わかりやすくなるように努力はしたものの理解は難しいかもしれない．そこで全ての図をGeoGebraのデータとして こちら に公開する．これらも参考にしながら読み進めれば理解も捗るだろう．それでは前置きはこの程度にして早速本題に入ろう．

フランク・モーリーの定理って？

$2000$年以上も前から続いてきたにもかかわらず，最近になっても美しい定理が見つかり続けるというのは初等幾何の世界の魅力だろう．フランク・モーリーの定理もそのような定理のひとつで，発見されたのは今から約$120$年前の$1899$年．初等幾何の世界ではかなり新しい定理である．実用性は皆無であるものの，この神秘的な美しさを放つこの定理．ここまで美しい定理がまだ残されていたという衝撃はきっと大きなものだっただろう．定理の主張は以下の通りである．

フランク・モーリーの定理

証明については参考文献[2]に三角関数の計算によるものがあるので興味のある者はそちらを参考にしてほしい．
　美しさは図を見ていただければよくわかってもらえると思う．私はこの美しさに惹かれてかれこれ数年はモーリーの定理信者を続けている．余談だが，角の三等分線はコンパスと定規で作図できないため上の図も作図不可能であり，これも個人的には美しいポイントのひとつである．フリーハンドで書こうものならそれはそれはひどい図が出来上がるだろう．ぜひ一度書いてみてほしい．

定理は拡張したい

定理を見れば拡張したくなるもの．それはモーリーの定理でも例外ではなく，この定理を拡張してより美しい世界を見ようとする者がいた．ここから先はF.G.Taylor,W.L.Marrによるこの方面での結果[1]を紹介する．
　一口に拡張といえども，その方針は多岐にわたる．$n$角形で考えてみたり，$n$等分線を考えてみたり，さまざまなことが考えられる．ここで彼らが着目したのは「角の三等分線の取り方」であった．はじめに，内角の二等分線の交点で内心を得られたのを外角の二等分線の交点にしてみることで傍心が得られたように，内角の三等分線を外角の三等分線にしてうまくいかないかということを考える．これを実際に図にすると以下のようになる．
このとおり，正三角形が現れた．これを定理としてまとめる．

外角におけるフランク・モーリーの定理

証明は内角の場合と全く同様にできるのだが，なぜこのようにうまくいくのだろうか．内角と外角の三等分線を比較すると，簡単な計算によって単に$120^\circ$ずれただけだということがわかる．$360^\circ$の$\frac 13$．もうお分かりだろうか．これは例えば$60^\circ$の三等分を考えたときに，普通に$20^\circ$とするか，あるいは$60^\circ = 60^\circ + 360^\circ$だと考えて$140^\circ$だとするかという違いであって，内角と外角の三等分線は本質的に全く同じものなのである．ここまで来れば，内角の三等分線から$240^\circ$ずらした「三つ目の三等分線」を考えたくなるのは自然な発想である．$180^\circ$から内角だけ引いた部分を外角と呼ぶように，$360^\circ$から内角だけ引いた部分を優角と呼ぶことにすれば，実はこの三つ目の三等分線は優角の三等分線となる．

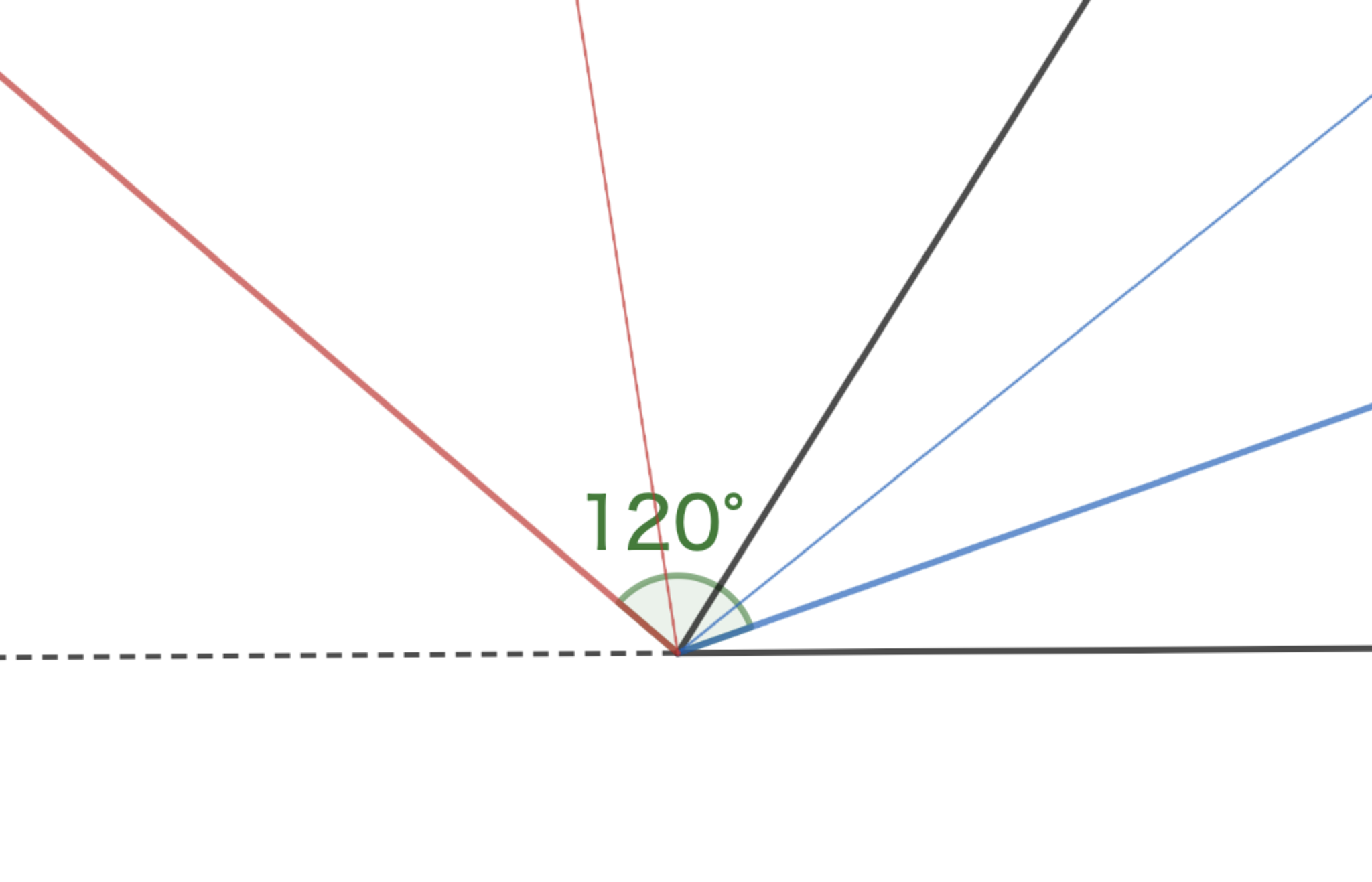内角と外角の三等分線

優角とその三等分線

そして優角での三等分線でも交点をとってみると想像通り正三角形が現れる．

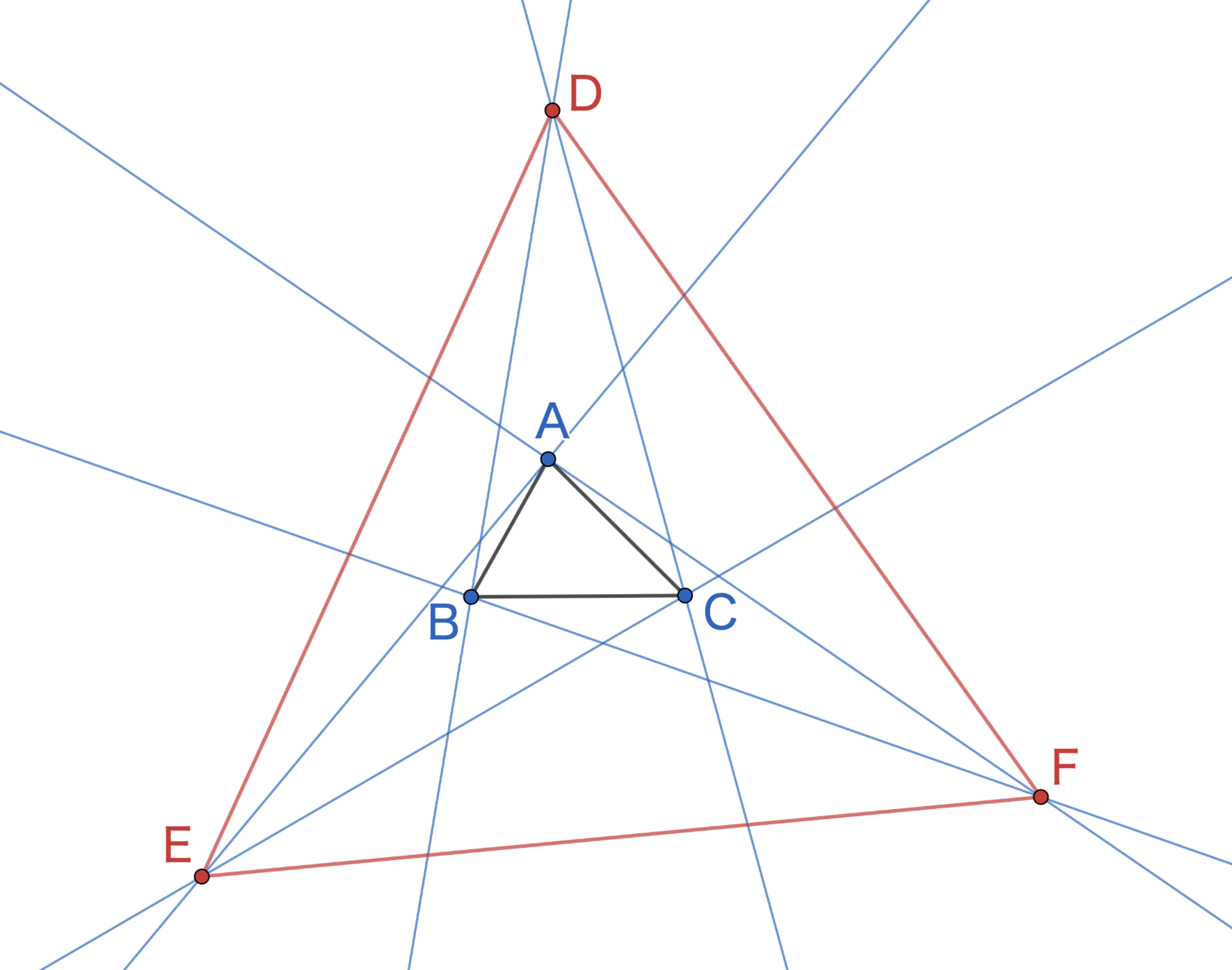優角におけるフランク・モーリーの定理

定理の形にまとめると以下のとおり．

なお優角というのは正しい用語ではない．一般に優角といえば$180^\circ < \theta < 360^\circ$であるような角を指す言葉であって，多角形の外側の角を指すものではない．そもそも三角形以外では外側の角が$180^\circ$より大きいとは限らないから全くもって適切ではないのだが，三角形に限れば外側が本来の優角の意味に合致することが保障されるから今回はこの語を用いることにした．
　さて，角の三等分線には$3$種類の取り方があって，それぞれに対してモーリーの定理と同様のことを考えられることがわかったのだが，これで終わりではない．内角の三等分線同士というように，同じ種類の三等分線同士の交点しかまだとっていないではないか．せっかく色々な三等分線をとったのだからもっと色々な三等分線をとってみよう．
　内角，外角，優角にそれぞれ$0,1,2$の番号を与え，例えば$\angle \mathrm B$の内角と$\angle \mathrm C$の外角の三等分線の交点が$\mathrm D_{01}$というように添え字に三等分線の種類の番号をつけることでこれらに$\mathrm D_{qr}, \mathrm E_{rp}, \mathrm F_{pq}$と名前をつける．これらを図示すると次の図のようになる．

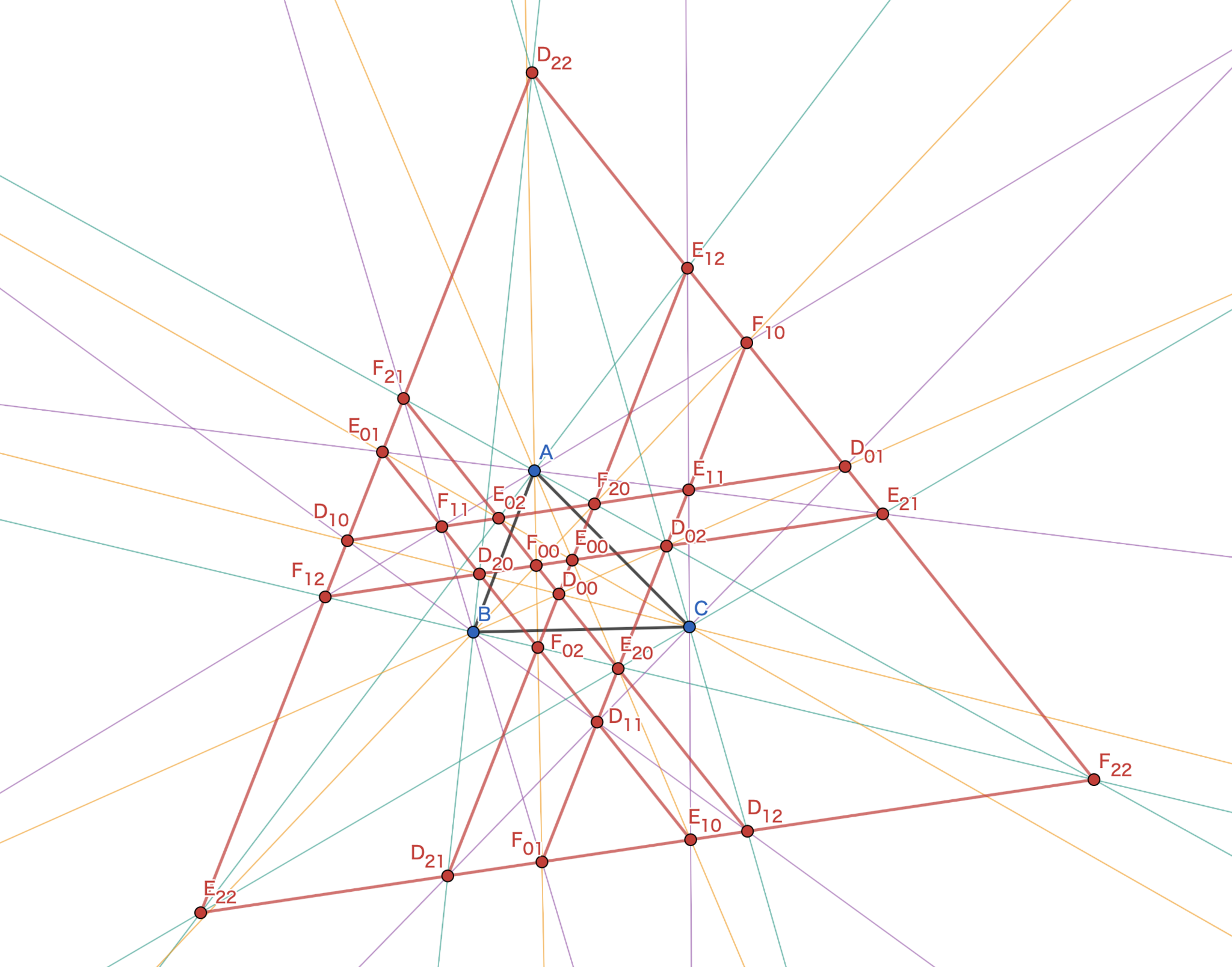モーリーの定理の拡張

これを初めて見たときの感動といったらすごかった（語彙力）．私はこの図のように大量の正三角形が現れるという事実をモーリーの定理の拡張と呼んでいる．一度，定理の形にまとめておこう．

この定理の証明を与えるには三線座標と呼ばれるものが必要である．

三線座標に関して，詳しくは[3]を参照してほしい．以下，座標といえばこの三線座標を指すものとする．
　はじめに示すのは，$6$点が同一直線上にあるということである．
　$\alpha_p=\frac {\mathrm A}3 + \frac {2p}3 \pi, \beta_q=\frac {\mathrm B}3 + \frac {2q}3 \pi, \gamma_r=\frac {\mathrm C}3 + \frac {2r}3 \pi$とすると，簡単な計算により$\mathrm D_{qr}$の座標が$(1, 2\cos \gamma_r, 2\cos \beta_q)$で表せることがわかる．$\mathrm E_{rp}, \mathrm F_{pq}$も同様である．したがっての座標は$(2\cos \gamma_0, 1, 2\cos \alpha_0), (2\cos \beta_0, 2\cos \alpha_0, 1)$と表せるので，頑張ってこの$2$点を通る直線を求めると$\alpha\sin\alpha_2 + \beta\sin\beta_1 + \gamma\sin\gamma_1=0$となる．ここで$\alpha_p, \beta_q$を$\alpha_{p-1}, \beta_{q+1}$に変換し，さらに$\mathrm {A,B,C}$を$\mathrm {C,A,B}$に入れ替えて同様のことを考える．これによって，$\mathrm {E_{00},F_{00}}$は$\mathrm {D_{02},E_{21}}$へと移るのだが，これらを結ぶ直線の式は変化しないということがわかる．さらに$alpha_p, \gamma_r$を$\alpha_{p-1}, \gamma_{r+1}$に変換し，$\mathrm {A,B,C}$を$\mathrm {B,C,A}$に入れ替えてみる．これによって，$\mathrm {E_{00},F_{00}}$は$\mathrm {F_{21}, D_{20}}$へと移るが，この場合にもこれらを結ぶ直線の式は変化しない．したがってこの式の上に$\mathrm {E_{00},F_{00},D_{02},E{21},F_{21}, D_{20}}$が全てあるということがわかる．残りの$8$本の直線に関しても同様の証明ができるだろう．
　次に$3$組の平行な直線が現れることを証明しよう．ここでは$\mathrm{E_{00}F_{00} \parallel E_{11}F_{11} \parallel E_{22}F_{22}}$を示す．$\mathrm {\triangle AE_{00}C \sim \triangle ABF_{01}, \triangle AF_{00}B \sim \triangle ACE_{10}}$がわかるので，
$$ \mathrm { \frac {AE_{00}}{AC} = \frac {AB}{AF_{01}}, \frac {AF_{00}}{AB} = \frac {AC}{AE_{10}}; \therefore \frac {AE_{00}}{AF_{00}} = \frac {AE_{10}}{AF_{01}} } $$
を得る．これは$\mathrm {E_{00}F_{00} \parallel E_{10}F_{01}}$すなわち$\mathrm {E_{00}F_{00} \parallel E_{22}F_{22}}$を示している．残りの直線についても同様に示すことができる．

射影的な話

射影幾何学という考え方がある．厳密な定義は他にあるが，ユークリッド平面においては$3$点が同一直線上に並ぶ共線性と，$3$直線が一点で交わる共点性について考える幾何学といって良いだろう．射影幾何学の世界はその性質上，長さや角度といった計量の概念を扱うことを苦手とする．角の三等分線やら正三角形やらとはいかにも相性が悪い．ここからはそんなモーリーの定理に隠れた射影的な側面の話をしよう．
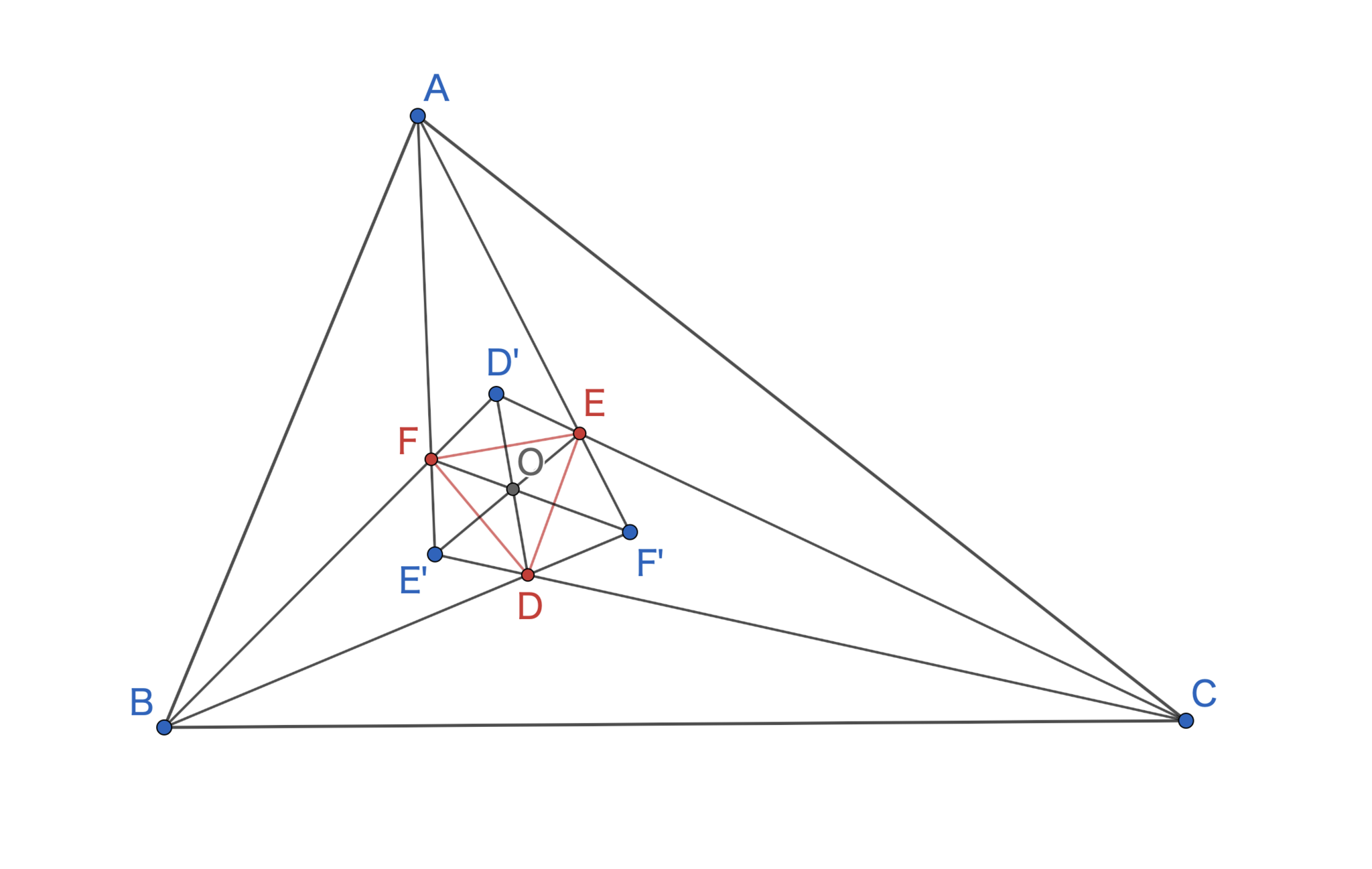
　例のごとく内角の三等分線をとり，その交点$\mathrm {D,E,F,D',E',F'}$を図のようにとる．$\triangle \mathrm {DEF}$がモーリーの定理における正三角形である．もしや$\triangle \mathrm {D’E'F'}$も正三角形に！？と思った読者もいるだろうが，図からわかるように残念ながら正三角形になるとは限らない．さらに$\mathrm{AD}$と$\mathrm{BC}$，$\mathrm{BE}$と$\mathrm{CA}$，$\mathrm{CF}$と$\mathrm{AB}$の交点をそれぞれ$\mathrm{X,Y,Z}$とし，$\mathrm{D,E,F}$から$\mathrm{BC,CA,AB}$におろした垂線をそれぞれ$\mathrm{X_D,Y_D,Z_D;X_E,Y_E,Z_E;X_F,Y_F,Z_F}$とする（煩雑なので図には示さない．GeoGebraには非表示で点をとっている）．

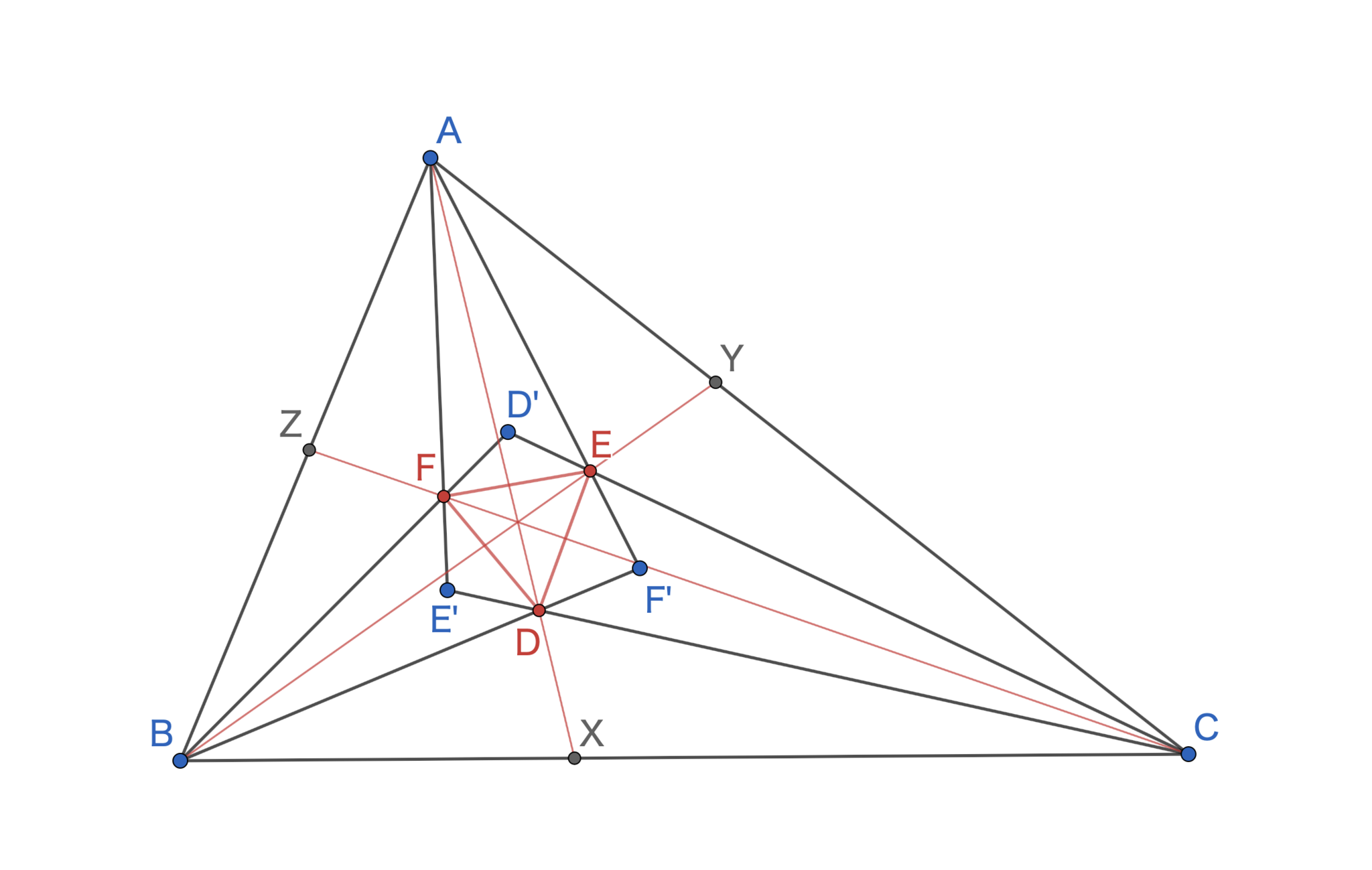図に名前をつけないといけない仕様に困っています

このときいくつかの三角形の相似から
$$\mathrm{\frac{EZ_E}{EY_E}=\frac{FY_F}{FZ_F}, \frac{FX_F}{FZ_F}=\frac{DZ_D}{DX_D}, \frac{DY_D}{DX_D}=\frac{EX_E}{EY_E}}$$
が成り立つので
$$ \begin{aligned} \mathrm{\frac{BX}{XC} \cdot \frac{CY}{YA} \cdot \frac{AZ}{AB} } &= \mathrm{\frac{\triangle ADB}{\triangle ADC} \cdot \frac{\triangle BEC}{\triangle BEA} \cdot \frac{\triangle CFA}{\triangle CFB} }\\ &= \mathrm{\frac{DZ_D \cdot AB}{DY_D \cdot AC} \cdot \frac{EX_E \cdot BC}{EZ_E \cdot BA} \cdot \frac{FY_F \cdot CA}{FX_F \cdot CB} }\\ &=1 \end{aligned} $$
これによって$3$直線$\mathrm {AD,BE,CF}$が共点であることが示された．一度共点性が示されてしまえば，あとは射影的な手法でいくらでも議論できる．ここではブリアンションの定理を用いる．

$\mathrm {AD, BE, CF}$が共点だったので，補題から六角形$\mathrm {AFBDCE}$の全てに接する二次曲線が存在する．ここで$2$つの六角形$\mathrm {AE'CD'BF', D'FE'DF'E}$について考えると$\mathrm {AFBDCE}$と同じ辺を持っていることがわかるので，再び補題から$\mathrm {AE'CD'BF'}$において$3$直線$\mathrm {AD', BE', CF'}$が，$\mathrm {D'FE'DF'E}$において$3$直線$\mathrm {DD', EE', FF'}$が共点であることがわかる．
$\mathrm {DD', EE', FF'}$の交点，$\mathrm {AD, BE, CF}$の交点，$\mathrm {AD', BE', CF'}$の交点をそれぞれ$\mathrm {M_1, T_1, T_2}$とする．さらなる射影幾何の定理，デザルグの定理を使えば面白いことがわかる．

$\mathrm {\triangle D'EF, \triangle DE'F'}$で$\mathrm {DD',EE',FF'}$は共点だったので，デザルグの定理によって$\mathrm {EF,E'F'}$の交点と$\mathrm {B,C}$の$3$点が共線である，すなわち$3$直線$\mathrm {BC, EF, E'F'}$が共点であることがわかる．続いて$\mathrm {\triangle BEE', \triangle CFF'}$で，この共点から再びデザルグの定理により$\mathrm {EE', FF'}$の交点，$\mathrm {BE, CF}$の交点，$\mathrm {BE', CF'}$の交点の$3$点が共線とわかるのだが，この交点は$\mathrm {M_1, T_1, T_2}$にほかならない．これで以下の定理が得られた．

モーリーの定理における共点・共線

図８の中心付近の拡大図

次に同様のことをモーリーの定理の拡張に対しても考えるのだが，ほとんど同じ議論で単調なので一部だけを紹介して残りは読者に任せることにする．
　$\mathrm D_{qr}, \mathrm E_{rp}, \mathrm F_{pq}$の記法を思い出し，$\mathrm {D,E,F}$に対して$\mathrm D_{qr}, \mathrm E_{rp}, \mathrm F_{pq}$を定義したのと同じように$\mathrm {D',E',F'}$に対して$\mathrm D'_{qr}, \mathrm E'_{rp}, \mathrm F'_{pq}$を定める．外角におけるモーリーの定理において共点性の議論をすると，$\mathrm {D_{11}D'_{11}, E_{11}E'_{11}, F_{11}F'_{11}}$の$3$本，$\mathrm {A_{11}D_{11}, B_{11}E_{11}, C_{11}F_{11}}$の$3$本，$\mathrm {A_{11}D'_{11}, B_{11}E'_{11}, C_{11}F'_{11}}$の$3$本が共点であることがわかるので，この交点をそれぞれ$\mathrm {M_2, T_3, T_4}$とする．同様に優角におけるモーリーの定理において共点性の議論をすると，$\mathrm {D_{22}D'_{22}, E_{22}E'_{22}, F_{22}F'_{22}}$の$3$本，$\mathrm {A_{22}D_{22}, B_{22}E_{22}, C_{22}F_{22}}$の$3$本，$\mathrm {A_{22}D'_{22}, B_{22}E'_{22}, C_{22}F'_{22}}$の$3$本が共点であることがわかるので，この交点をそれぞれ$\mathrm {M_3, T_5, T_6}$とする．当然$\mathrm {M_2, T_3, T_4}$と$\mathrm {M_3, T_5, T_6}$はそれぞれ共線なのだが，実際にはより強く以下が成り立つ．

静止画では全く理解できないほど複雑な図なので，図は省略する．配布しているGeoGebraのファイルには作図したものを入れているので，そちらを確認してほしい．また，証明に関しては三線座標などによって容易にできるから各自で試みられたい．

モーリーの定理の別証

この共点・共線性を利用するとモーリーの定理を証明できる．
　まず$\triangle \mathrm {BCD'}$に注目する．$\mathrm{\angle CBD = \angle D'BD, \angle BCD = \angle D'CD}$であることから$\mathrm D$が内心となることがわかる．よって$\mathrm{\angle BD'D = \angle CD'D}$．同様に$\mathrm{\angle CE'E = \angle AE'E, \angle AF'F = \angle BF'F}$がわかる．これより簡単な角度計算から$\mathrm{\angle M_1E'D=60^\circ+\frac B3, \angle M_1FD=60^\circ+\frac C3, \angle E'DF'=120^\circ+\frac A3}$とわかるので，$\mathrm{\angle E'M_1F'=120^\circ}$すなわち$\mathrm{\angle EM_1F'=\angle FM_1E'=60^\circ}$．よって$\mathrm{\triangle EM_1D' \equiv \triangle FM_1D'}$なので$\mathrm {ED'=FD'}$となり，さらに$\mathrm{\triangle EM_1D' \equiv \triangle FM_1D'}$から$\mathrm {DE=DF}$である．よって$\mathrm {DE=EF=FD}$が分かったので$\mathrm {\triangle DEF}$は正三角形である．
　この議論で$\mathrm {DD',EE',FF'}$の共点性が用いられたことに注意してほしい．

モーリーの定理の別証

問題

本文中で紹介できなかったいくつかの事実に関して，問題の形で事実だけ述べる．答えに関しては[1]に詳しい．

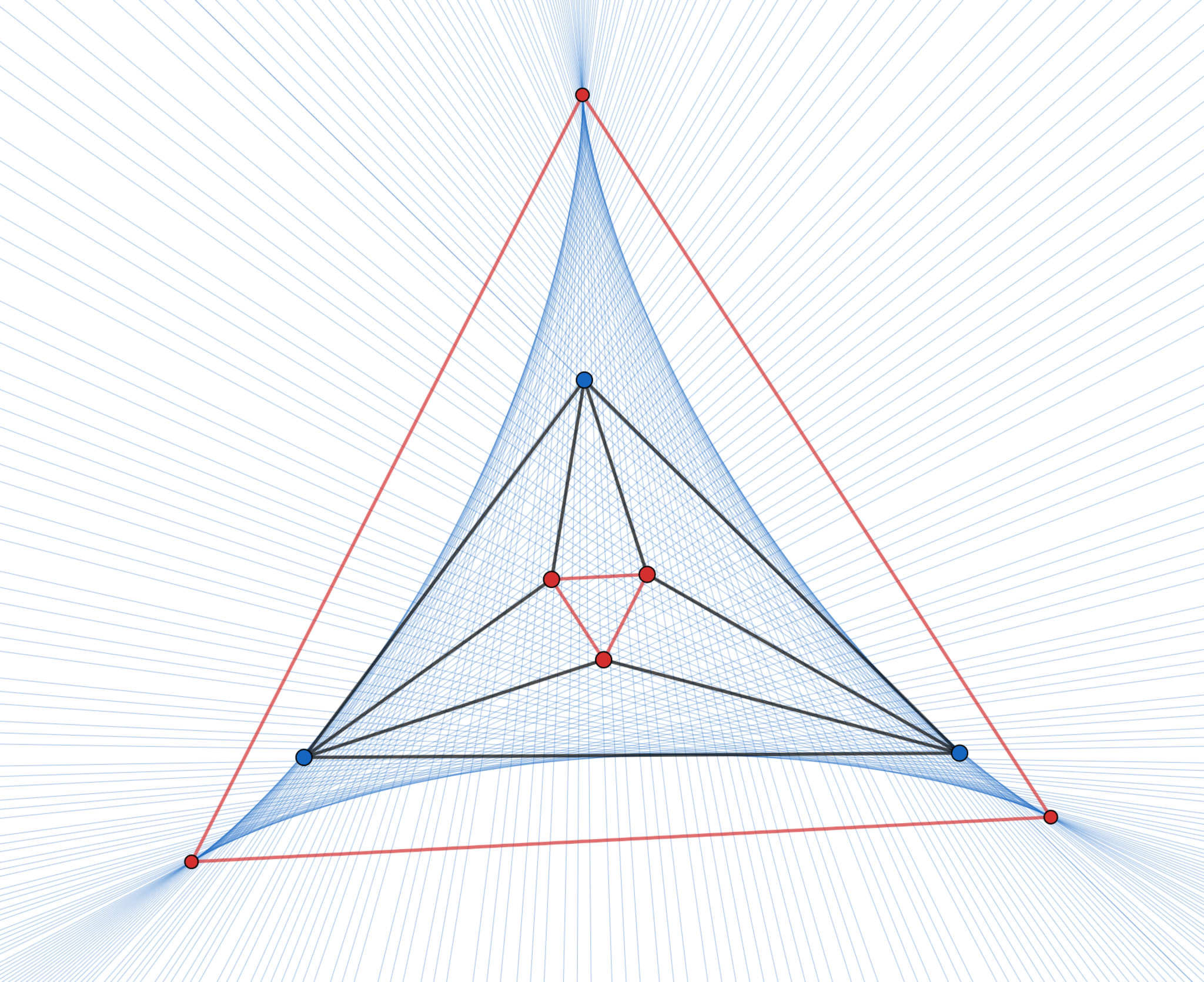モーリーの定理とsteinerのデルトイド

この問題は[1]では触れられていない．詳しくは[4]を参照されたい．

おわりに

ここまでモーリーの定理について書いてきたが，いかがだっただろうか．少しでも面白いと思ってもらえたならば嬉しい．もしモーリーの定理に興味を持ってもっと深く知りたいと思ったならば，ぜひとも[1]を読んでほしい．英語論文であって少々敷居が高いものの，ここで紹介しきれなかった面白い事実がたくさん載っている．そしてなにか面白いことが分かったならば，是非とも私に教えてもらえれば嬉しい．
　クリスマスまであと$2$週間．数学が恋人だった去年に続き，今年は受験勉強と一夜を過ごすことになりそうだ．来年こそは本当の恋人と……