重心座標系・三線座標系についてのまとめ
はじめに
三角形についていろいろ調べていると、'三線座標'や'重心座標'といった三角形に相対的な位置の表現がよく用いられる。また解析幾何的証明法にも利用される。これらの基本的な性質について、自分にはあまり自明でないことも多かったので、行間を埋めつつここにまとめる。
目次
- 定義と基本性質
$\to$
内容
定義1: 重心座標 $\to$
定義2: 三線座標 $\to$
系1: 重心座標と面積比 $\to$
定理1: 重心座標と三線座標の変換 $\to$
系2: 座標の定数倍 $\to$
定理2: デカルト座標と重心座標の変換 $\to$ - 重心座標系の直線 $\to$
- 重心座標系の円錐曲線 $\to$
- 2021/01/20 初稿
- 2021/01/26 円錐曲線の内接について加筆
1. 定義と基本性質
2次元平面上$\triangle\mr{ABC}$をおき、その座標をそれぞれ$\mr{A}(a_x,a_y)$などとする。位置ベクトル$\mr{A}(\vec{a})$、辺の長さ$\mr{BC}=a$もそれぞれ同様に定義する。
平面上の点$\mr{X}(\vec{x})$が、$\vec{x}=\dfrac{\xi_b\vec{a}+\eta_b\vec{b}+\zeta_b\vec{c}}{\xi_b+\eta_b+\zeta_b}$で表されるとき、$(\xi_b,\eta_b,\zeta_b)$を$\mr{X}$の重心座標という。ただし$\xi_b+\eta_b+\zeta_b\neq0$。
平面上の点$\mr{X}$が、直線$\mr{BC,CA,AB}$からの距離の比がそれぞれ$\xi_t,\eta_t,\zeta_t$であるとき、$(\xi_t,\eta_t,\zeta_t)$を点$\mr{X}$の三線座標という。点$\mr{X}$が、直線$\mr{BC}$に対して点$\mr{A}$と同じ側にあるとき$\xi_t>0$とし、反対側にあるとき$\xi_t<0$とする。$\eta_t,\zeta_t$についても同様に符号を定める。
以下のことがらが従うことは簡単にわかる。
符号を、3点が反時計回りに並ぶとき正、時計回りに並ぶとき負と定める符号付き面積について、
$\triangle\mr{XBC}:\triangle\mr{XCA}:\triangle\mr{XAB}=\xi_b:\eta_b:\zeta_b$である。
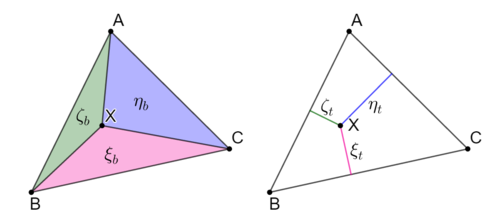 座標系の模式図
座標系の模式図
座標を模式的に示すと上図のようになる。これを踏まえて、座標の変換を考えることができる。
符号付き面積の比は、$\triangle\mr{XBC}:\triangle\mr{XCA}:\triangle\mr{XAB}=a\xi_t:b\eta_t:c\zeta_t$であることと、面積比と重心座標の関係から従う。
本来なら、2次元平面上の位置を表すのに3つの座標は必要ない。そのため、重心座標・三線座標と平面上の位置が厳密に1対1対応するわけではなく、次の性質を持つ。
点$\mr{X}$が重心座標で$(\xi_b,\eta_b,\zeta_b)$、三線座標で$(\xi_t,\eta_t,\zeta_t)$と表されるとき、$0$でない実数$k$を用いて重心座標$(k\xi_b,k\eta_b,k\zeta_b)$、三線座標$(k\xi_t,k\eta_t,k\zeta_t)$で表される点はともに点$\mr{X}$を表す。
重心座標については、定義から明らか。
三線座標で$(\xi_t,\eta_t,\zeta_t)$と表される点は、定理1より重心座標では$(a\xi_t,b\eta_t,c\zeta_t)$と表され、重心座標$(ka\xi_t,kb\eta_t,kc\zeta_t)$も同じ点を表す。このとき三線座標は$(k\xi_t,k\eta_t,k\zeta_t)$であるから、題意は示される。
通常、重心座標では$\xi_b+\eta_b+\zeta_b=1$となるように、三線座標では$\xi_t:\eta_t:\zeta_t$が簡単な比となるように選ばれる。なお、$\xi_t,\eta_t,\zeta_t$に各辺からの実際の距離を用いるなら、それを絶対三線座標と呼ぶ。
点$\mr{X}$は、デカルト座標で$(x,y)$、重心座標で$(\xi_b,\eta_b,\zeta_b)$、とそれぞれ表される。ただし$\xi_b+\eta_b+\zeta_b=1$とする。このとき次が成り立つ。
\begin{aligned}
\begin{pmatrix}
a_x & b_x & c_x \\
a_y & b_y & c_y \\
1 & 1 & 1
\end{pmatrix}
\begin{pmatrix}
\xi_b \\
\eta_b \\
\zeta_b
\end{pmatrix}
=
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
\end{aligned}
重心座標の定義と与えられた束縛条件から直ちに得られる。
三角形の代表的な点の重心座標・三線座標は文献を参照すればたくさん載っている。
2. 重心座標系の直線
ここでは重心座標$(\xi_b,\eta_b,\zeta_b)$を用いて議論するが、 定理1 を援用しつつ係数を適宜調整することで三線座標でも形式的に同じ結果が得られることを注意しておく。
相異なる2点$\mr{P}(p,q,r)$, $\mr{U}(u,v,w)$を通る直線を表す方程式は
\begin{aligned}
\begin{vmatrix}
\xi_b & \eta_b & \zeta_b \\
p & q & r \\
u & v & w
\end{vmatrix}
=0 \quad\dou\quad (qw-rv)\xi_b-(pw-ru)\eta_b+(pv-qu)\zeta_b=0
\end{aligned}
点$\mr{X}(\xi_b,\eta_b,\zeta_b)$をとる。$p+q+r=u+v+w=\xi_b+\eta_b+\zeta_b=1$としてよい。点$\mr{X}$が直線$\mr{PU}$上にあることと、ある実数$t$を用いて$\vec{\mr{CX}}=t\vec{\mr{CP}}+(1-t)\vec{\mr{CU}}$と書けることは同値である。これは、$\vec{\mr{CX}}=\xi_b\vec{\mr{CA}}+\eta_b\vec{\mr{CB}}$などであることから
\begin{aligned}
(\xi_b-tp-(1-t)u)\vec{\mr{CA}}+(\eta_b-tq-(1-t)v)\vec{\mr{CB}}=\vec{0}
\end{aligned}
と表される。$\vec{\mr{CA}}$と$\vec{\mr{CB}}$は線形独立だから、
\begin{aligned}
\xi_b-tp-(1-t)u=\eta_b-tq-(1-t)v=0
\end{aligned}
である。これが$t$について解を持つためには、
\begin{aligned}
\frac{\xi_b-u}{p-u}=\frac{\eta_b-v}{q-v} \quad\dou\quad (\xi_b-u)(q-v)-(\eta_b-v)(p-u)=0
\end{aligned}
でなければならない。逆に、$\xi_b,\eta_b,p,q,u,v$がこれを満たすならば、$\dfrac{\xi_b-u}{p-u}=\dfrac{\eta_b-v}{q-v}$の値を$t$とすればよい。
\begin{aligned}
&(\xi_b-u)(q-v)-(\eta_b-v)(p-u)=
\begin{vmatrix}
\xi_b-u & \eta_b-v \\
p-u & q-v
\end{vmatrix} =
\begin{vmatrix}
\xi_b-u & \eta_b-v & 1 \\
p-u & q-v & 1 \\
0 & 0 & 1
\end{vmatrix} \\
=&\, \begin{vmatrix}
\xi_b & \eta_b & 1 \\
p & q & 1 \\
u & v & 1
\end{vmatrix} =
\begin{vmatrix}
\xi_b & \eta_b & 1-\xi_b-\eta_b \\
p & q & 1-p-q \\
u & v & 1-u-v
\end{vmatrix} =
\begin{vmatrix}
\xi_b & \eta_b & \zeta_b \\
p & q & r \\
u & v & w
\end{vmatrix}
\end{aligned}
であるから、題意は示された。
3点$\mr{L}(l,m,n)$, $\mr{P}(p,q,r)$, $\mr{U}(u,v,w)$が同一直線上にあることは、
$\begin{vmatrix}
l & m & n \\
p & q & r \\
u & v & w
\end{vmatrix}=0$ であることと同値である。
定理3 より、点$\mr{L}$は直線$\mr{PU}$上にあることを意味するからよい。
定理3
より、直線を表す方程式がこのようにあらわされることは明らか。
逆に、点$\mr{X}(\xi_b,\eta_b,\zeta_b;\vec{x})$ ($\xi_b+\eta_b+\zeta_b=1$) が方程式$l\xi_b+m\eta_b+n\zeta_b=0$を満たすとする。明らかに$l=m=n$ではないから、少なくとも2つは相異なる。$m\neq n$の場合を示すが、$m=n$の場合でも$l\neq m,n$は成り立つから同様の議論が成立することに注意する。$\xi_b=t$として、
$$
\eta_b=\frac{-n}{m-n}+t\cdot\frac{-l+n}{m-n} \,,\,\, \zeta_b=\frac{m}{m-n}+t\cdot\frac{l-m}{m-n}
$$
であるから、
\begin{aligned}
\vec{x}&=t\vec{a}+\left(\frac{-n}{m-n}+t\cdot\frac{-l+n}{m-n}\right)\vec{b}+\left(\frac{m}{m-n}+t\cdot\frac{l-m}{m-n}\right)\vec{c} \\
&=\left(\frac{-n}{m-n}\vec{b}+\frac{m}{m-n}\vec{c}\right)+t\left(\vec{a}+\frac{-l+n}{m-n}\vec{b}+\frac{l-m}{m-n}\vec{c}\right)
\end{aligned}
となるので、これは直線を表す。よって題意は示された。
3直線$l_1\xi_b+m_1\eta_b+n_1\zeta_b=0$, $l_2\xi_b+m_2\eta_b+n_2\zeta_b=0$, $l_3\xi_b+m_3\eta_b+n_3\zeta_b=0$ が1点で交わることは、
$
\begin{vmatrix}
l_1 & m_1 & n_1 \\
l_2 & m_2 & n_2 \\
l_3 & m_3 & n_3
\end{vmatrix}=0
$と同値である。
3直線が1点で交わるとき、その点を$\mr{P}(p,q,r)$とすれば以下が成り立つ。
\begin{aligned}
\begin{pmatrix}
l_1 & m_1 & n_1 \\
l_2 & m_2 & n_2 \\
l_3 & m_3 & n_3 \\
\end{pmatrix}\!
\begin{pmatrix}
p \\
q \\
r
\end{pmatrix}
=O
\end{aligned}
これは$(p,q,r)=(0,0,0)$を自明な解として持つが、点$\mr{P}$を表す重心座標としては不適。よって非自明な解$(p,q,r)$を持たなければならないので、
$
\begin{vmatrix}
l_1 & m_1 & n_1 \\
l_2 & m_2 & n_2 \\
l_3 & m_3 & n_3
\end{vmatrix}=0
$
でなければならない。逆にこれが成り立つとき、非自明な$(p,q,r)$の解が存在するので、そのような点$\mr{P}(p,q,r)$で3直線は一点で交わる。
3. 重心座標系の円錐曲線
ここでも重心座標$(\xi_b,\eta_b,\zeta_b)$を用いて議論する。三線座標への変換についての注意も同様。
重心座標において円錐曲線 (楕円・放物線・双曲線) を表す方程式は、
\begin{aligned}
&
\begin{pmatrix}
\xi_b & \eta_b & \zeta_b
\end{pmatrix}\!
\begin{pmatrix}
p & l & m \\
l & q & n \\
m & n & r
\end{pmatrix}\!
\begin{pmatrix}
\xi_b \\ \eta_b \\ \zeta_b
\end{pmatrix}=0 \\
\dou\quad & p\xi_b^2+q\eta_b^2+r\zeta_b^2+2l\xi_b\eta_b+2m\eta_b\zeta_b+2n\zeta_b\xi_b=0
\end{aligned}
デカルト座標$(x,y)$上で、円錐曲線は一般に
$$ px^2+qy^2+2rxy+2sx+2ty+u=0 \quad\dou\quad
\begin{pmatrix}
x & y & 1
\end{pmatrix}\!
\begin{pmatrix}
p & r & s \\
r & q & t \\
s & t & u
\end{pmatrix}\!\!
\begin{pmatrix}
x \\ y \\ 1
\end{pmatrix}=0 $$
と表される。この$3\times3$行列を$A$とし、定理2におけるデカルト座標と重心座標の変換行列を$B$とすると、
\begin{aligned}
\begin{pmatrix}
x & y & 1
\end{pmatrix}
A
\begin{pmatrix}
x \\ y \\ 1
\end{pmatrix}
=
\begin{pmatrix}
\xi_n & \eta_b & \zeta_b
\end{pmatrix}
{}^tBAB
\begin{pmatrix}
\xi_b \\ \eta_b \\ \zeta_b
\end{pmatrix}
\end{aligned}
$A$は対称行列であり、${}^tB$と$B$は互いに転置であることに注意して計算すれば、${}^tBAB$は対称行列となることがわかる。よって題意が示された。
デカルト座標における方程式では、2次形式による表現行列の行列式を調べることで円錐曲線を分類できるが、重心座標における表現での分類法は明らかでないし、この表現形にはたとえば2直線も含まれうる。
各頂点は重心座標で$\mr{A}(1,0,0)$, $\mr{B}(0,1,0)$, $\mr{C}(0,0,1)$と表されるから、これらを通るならば 定理5 において$p=q=r=0$である。$2l\to l$などと係数を取り直せば題意の式が得られる。
この式は円錐曲線が外接するならば満たすべき式であり、ある式が与えられた場合にそれがどのような形状なのかを判断するには至らないことには注意する。
$\triangle\mr{ABC}$の頂点を除く外接円上に点$\mr{P}$を取る。面積の絶対値の比は
$$ |\triangle\mr{PBC}|:|\triangle\mr{PCA}|:|\triangle\mr{PAB}|=\frac{1}{2}\mr{PB\cdot PC}\sin\mr{A}:\frac{1}{2}\mr{PC\cdot PA}\sin\mr{B}:\frac{1}{2}\mr{PA\cdot PB}\sin\mr{C}=|\xi_b|:|\eta_b|:|\zeta_b| $$
 外接円と点Pの例
外接円と点Pの例
点$\mr{P}$が弧$\mr{BC}$間 ($\angle\mr{A}$内) にある場合を考える。すると$\triangle\mr{PBC}<0$,$\triangle\mr{PCA},\triangle\mr{PAB}>0$であるから、
\begin{aligned}
&a^2\eta_b\zeta_b+b^2\zeta_b\xi_b+c^2\xi_b\eta_b=\frac{\mr{PA\cdot PB\cdot PC}}{4}(a^2\mr{PA}\sin\mr{B}\sin\mr{C}-b^2\mr{PB}\sin\mr{C}\sin\mr{A}-c^2\mr{PC}\sin\mr{A}\sin\mr{B})) \\
=&\,\frac{1}{2}R\cdot\mr{PA\cdot PB\cdot PC}\sin\mr{A}\sin\mr{B}\sin\mr{C}(a\mr{PA}-b\mr{PB}-c\mr{PC})
\end{aligned}
なお$R$は外接円半径。トレミーの定理により、$a\mr{PA}=b\mr{PB}+c\mr{PC}$が成り立つから、この式の値は$0$となる。点$\mr{P}$が他の弧上にあるときにも、負の面積となる三角形が変わることとトレミーの定理の表式が変わることに注意すれば、常にこの式の値は$0$となる。
よって題意は示された。
頂点を除いた3辺$\mr{BC,CA,AB}$上あるいはその延長線上で接する円錐曲線は
$$ p^2\xi_b^2+q^2\eta_b^2+r^2\zeta_b^2-2pq\xi_b\eta_b-2qr\eta_b\zeta_b-2rp\zeta_b\xi_b=0 $$
で表され、接点の重心座標はそれぞれ$(0,r,q)$, $(r,0,p)$, $(q,p,0)$である。ただし$p,q,r\neq 0$。
辺$\mr{BC}$を表す方程式は$\xi_b=0$であるから、
定理5
において$\xi_b=0$とした式$q\eta_b^2+r\zeta_b^2+2m\eta_b\zeta_b=0$が重解をもつ。$q$(あるいは$r$)が$0$とすると、$\zeta_b$(あるいは$\eta_b$)が$0$となる解が得られるが、これは$\xi_b=0$と合わせて頂点を表すので不適。よってこのとき$m^2=qr>0$が成り立つから、$q$と$r$は同符号。よって$q,r,m$をそれぞれ$q^2,r^2,-qr$と置き換えることができ、このとき重解は$q\eta_b=r\zeta_b$、すなわち$\eta_b:\zeta_b=r:q$。
辺$\mr{CA,AB}$と接する条件についても同様の議論ができ、題意の式を得る。
$\triangle\mr{ABC}$に内接する円錐曲線
$$ p^2\xi_b^2+q^2\eta_b^2+r^2\zeta_b^2-2pq\xi_b\eta_b-2qr\eta_b\zeta_b-2rp\zeta_b\xi_b=0 $$
の中心の重心座標は、$(q+r,r+p,p+q)$である。
平行する2つの接線による接点の中点が中心となる。辺$\mr{AB}$に平行な直線は$\zeta_b=\alpha$で表されるから、この直線が与えられた円錐曲線と接するような$\alpha$の値とその時の接点の座標を求めればよい。また$\xi_b+\eta_b+\zeta_b=1$なる解を考えれば十分なので、$\eta_b=1-\alpha-\xi_b$を考える。$\beta=1-\alpha$とおいて、
\begin{aligned}
& p^2\xi_b^2+q^2(\beta-\xi_b)^2+r^2\alpha^2-2pq\xi_b(\beta-\xi_b)-2qr(\beta-\xi_b)\alpha-2rp\alpha\xi_b=0 \\
\dou\quad & (p+q)^2\xi_b^2-2(\beta q(p+q)+\alpha r(p-q))\xi_b+(\beta q-\alpha r)^2=0
\end{aligned}
これが$\xi_b$に関して重解を持てばよいから判別式$D$について
\begin{aligned}
\frac{D}{4}&=\beta^2q^2(p+q)^2+2qr\alpha\beta (p^2-q^2)+\alpha^2r^2(p-q)^2-(p+q)^2(\beta q-\alpha r)^2 \\
&=4pqr(p+q)\alpha\beta -4pqr^2\alpha^2=0
\end{aligned}
$\alpha=0$の解は辺$\mr{AB}$で接することを示すから、それ以外の解として$\alpha=\dfrac{p+q}{p+q+r}$を得て、そのときの接点の座標は
$$ \left(\dfrac{pr}{(p+q)(p+q+r)},\dfrac{qr}{(p+q)(p+q+r)},\dfrac{p+q}{p+q+r}\right) $$
与えられた円錐曲線の式について、$p,q,r$すべてを定数倍してもあらわす曲線は変わらないから、$p+q+r=1$であるとしてよい。また
系2
によって接点の座標は$(pr,qr,(p+q)^2)$と書ける。
続いて辺$\mr{AB}$での接点は$(q,p,0)$なので、これらの中点の座標は$(pr+q,qr+r,(p+q)^2)$となり、
\begin{aligned}
pr+q&=r(p+q)+(1-r)q=(q+r)(p+q) \\
qr+p&=r(p+q)+(1-r)p=(r+p)(p+q)
\end{aligned}
と計算できるから円錐曲線の中心は$(q+r,r+p,p+q)$。
あとがき
直線についてはおよそ満足しているが、円錐曲線についてはまだまだ不十分な点が多い。とくに形状の分類、焦点の座標が不足している。今後進展があれば追記・修正しようと思う。
