不変量を使ってポリオミノの問題を解く
はじめに
この記事は「
日曜数学 Advent Calendar 2022
」の 12月12日分の記事になります。
「12月12日」は、月と日を入れ替えても同じ日付になりますね!つまり不変・・・!!
……というわけで、この記事では不変量を使ってとある数学の問題を解いてみたいと思います。
(2022.12.12 追記)
※ 子葉さんのコメントでのご指摘にあわせて記号を修正しました。
不変量とは
不変量とは、たとえば「合同な図形の面積」とか「相似な図形の頂点数」のようなもののことです。ちゃんと定義するとこんな感じです。(Wikipedia調べ)
不変量（ふへんりょう、invariant）とは、数学的対象を特徴付ける別種の数学的対象のことである。一般に、不変量は数や多項式など、不変量同士の同型性判定がもとの対象の同型性判定より簡単であるものをとる。良い不変量とは、簡単に計算でき、かつなるべく強い同型性判別能力をもつものである。
とある問題
さて、この記事で挑戦する問題はみよしじゅんいち (@nosiika)さんの考案した次のようなものです。
Pペントミノからモノミノを引くと、テトロミノ5種のうち、Tテトロミノ、Lテトロミノ、Oテトロミノ、Sテトロミノの4種を作ることができる。引き算でテトロミノ5種を作ることができるようなポリオミノの組は存在するだろうか？
まず用語の説明をします。同じ大きさの正方形を辺に沿ってつなげた形を総称してポリオミノといいます。特に、正方形 $1$個、$2$個、$3$個、$4$個、$5$個、$6$個をつないだものはそれぞれ「モノミノ」、「ドミノ」、「トロミノ」、「テトロミノ」、「ペントミノ」、「ヘキソミノ」と呼びます(*)。そういえば、あえて名前は出しませんが、「テトロミノ」を並べて消すゲームは有名ですね。
(*) 語源としては「ドミノ」が最初
テトロミノは、裏返しや回転で一致するものを同一視すると５種類あり、区別するために似た形のアルファベットを用いてそれぞれ I型・O型・L型・S型・T型 と呼んだりします。
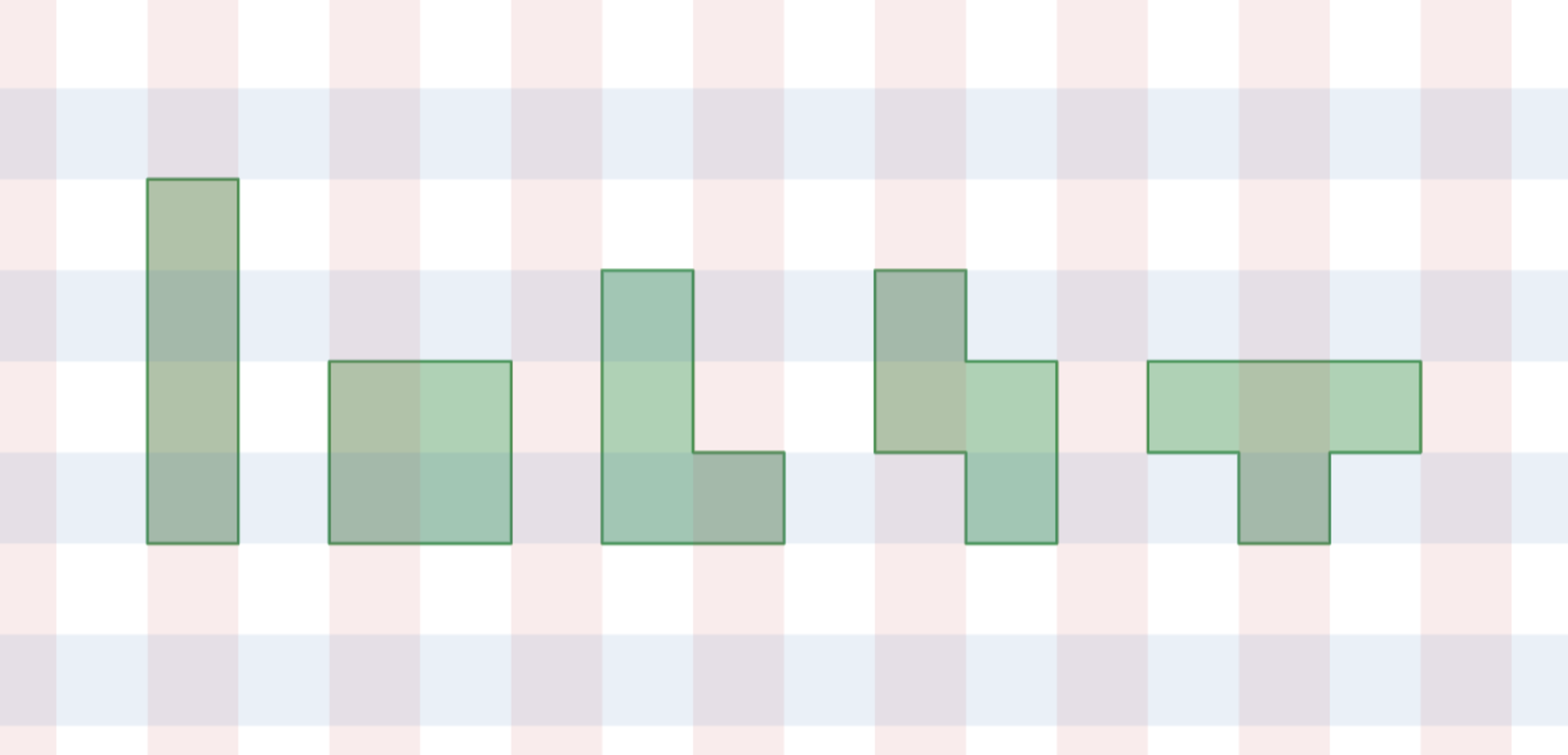テトロミノの I・O・L・S・T
そして、「Pペントミノからモノミノを引くと、テトロミノ5種のうち、Tテトロミノ、Lテトロミノ、Oテトロミノ、Sテトロミノの4種を作ることができる。」というのは、次の図のようにすれば、Pペントミノ(アルファベットのPに似た形のペントミノのことです。)からモノミノを削ることで4種のテトロミノが作れるということです。
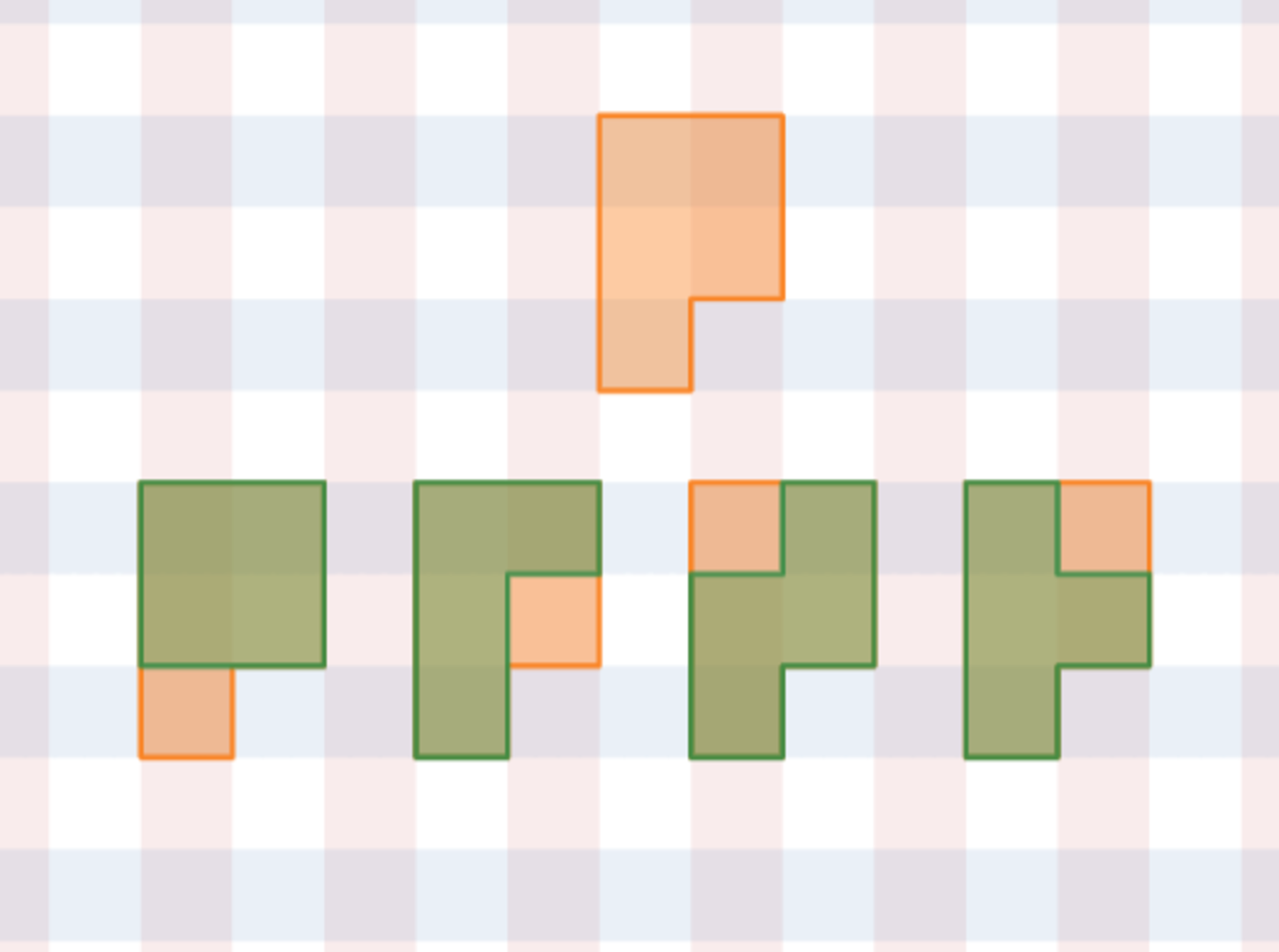PペントミノからO・L・S・Tのテトロミノが削り出せる
問題は、このようにポリオミノを「引き算」のように削った時に、テトロミノ $5$ 種をすべて作ることができるか、ということです。
試行錯誤してみる
とりあえず試行錯誤してみると、たとえばヘキソミノからドミノを削って $3$ 種類のテトロミノを作ったり、いろいろなパターンを作ることができます。
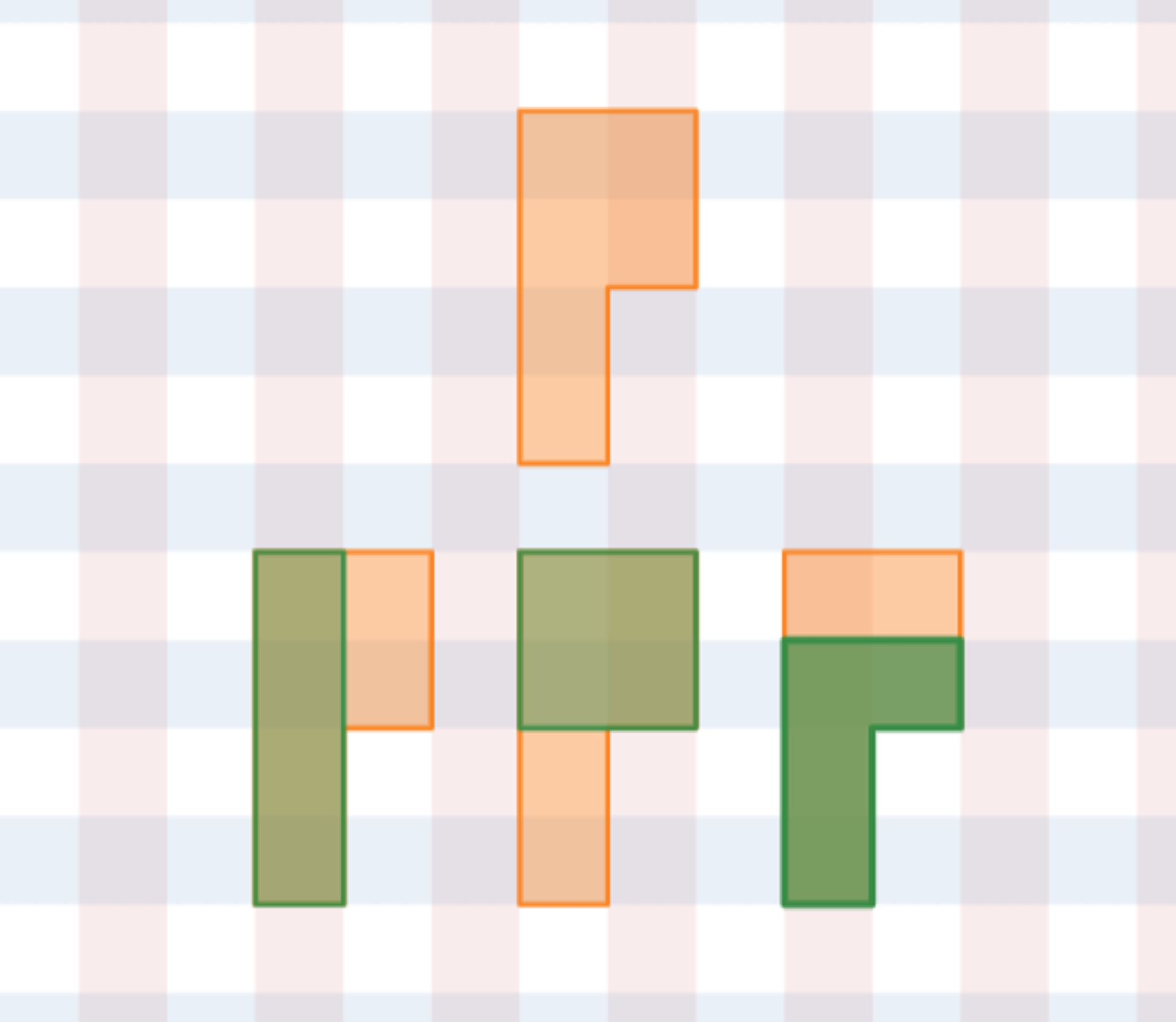ヘキソミノから I・O・L のテトロミノが削り出せる
しかしながら、$5$ 種全部を作るポリオミノの組み合わせはなかなか見つかりません。
しばらくやってみると「無理なのでは？」という気がしてきます。
となれば、不可能であることを証明したくなりますね!
不変量を使う(その1)
さて、最初に考えたのは以前「欠損チェスボードにドミノを敷き詰められるか」のときに使った、チェスボードの黒白のマスを数える方法でした。
そのときの記事を一部引用します。
欠損チェス盤にドミノ・L型トロミノ・I型トロミノを敷き詰めたい
=====(ここから引用)=====
欠損チェスボードにドミノを敷き詰められるか
=====(引用おわり)=====
このときと同じように、市松模様の上にテトロミノを並べてみます。
市松模様の上にテトロミノを配置する
そして、「テトロミノと重なる黒マスと白マスの個数の差」という量を考えます。
すると、その量は、テトロミノを平行移動・裏返し・回転しても変化しないことがわかります。つまり不変量……!!(伏線回収)
少し考えれば、テトロミノに限らず、一般的にポリオミノ全てについて「テトロミノと重なる黒マスと白マスの個数の差」は不変量となることがわかります。
ここでは、「ポリオミノ $x$ と重なる黒マスと白マスの個数の差」を $N(x)$ と書くことにします。また、Iテトロミノ・Oテトロミノ・Lテトロミノ・Sテトロミノ・Tのテトロミノはそれぞれ省略して単に $I,O,L,S,T$ と書くことにします。
表にするとこんな感じになります。
| N(I) | N(O) | N(L) | N(S) | N(T) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 2 |
$N(T)$ だけが違う数字になりました。これは使えそうな気がしますね?
次に、ポリオミノの「引き算」をすると、$N(x)$ がどのように変化するか考えてみましょう。
$N(x)$ は「ポリオミノ $x$ と重なる黒マスと白マスの個数の差」ですから、ポリオミノ $x$ からポリオミノ $y$ を削ったものを「$x-y$」で表すと、
$N(x-y)= \begin{cases} N(x)+N(y)\\ \,\text{ 又は }\,\\ \left|N(x)-N(y)\right| \end{cases} $
となります。
したがって、「Tテトロミノと、T以外のテトロミノをどちらも削り出せるポリオミノ $x,y$ の組合せが存在するならば、$N(x-y)$ が $0$ と $2$ の両方になる」はずです。
上記の式を満たす組み合わせを考えると
$ N(x)=1,N(y)=1$
しかありえないことがわかります。
偶数ミノ、奇数ミノ
突然ですが、正方形の数が偶数のポリオミノを「偶数ミノ」、奇数のポリオミノを「奇数ミノ」と呼ぶことにします。すると、次のようになります。
$N(\text{偶数ミノ})=\text{偶数}$
$N(\text{奇数ミノ})=\text{奇数}$
偶数を２つの整数に分けるとその偶奇が一致するから、その２つに分けた整数の差は偶数となる。
また、奇数を２つの整数に分けるとその偶奇は一致しないから、その２つに分けた整数の差も奇数となる。
したがって、$N(x)=1,N(y)=1$ をみたす $x,y$ はいずれも奇数ミノであることがわかります。
その1のまとめ
ここまでで、つぎのことがわかりました。
$T$テトロミノと、$T$以外のテトロミノをどちらも削り出せるポリオミノの組合せは、どちらも奇数ミノでなければならない
冒頭の例もこれを満たしていることを確認してください。
PペントミノからO・L・S・Tのテトロミノが削り出せる(再掲)
このアプローチでは、条件をみたすポリオミノの組合せが存在する場合には「奇数ミノと奇数ミノ」であること、特に、「黒マスと白マスの差が $1$ となる奇数ミノ」でなければならないことまではわかりましたが、そのような組み合わせが存在するかどうかまではわかりませんでした。
しかし、不変量はこれだけではありません。他の不変量が使えないかさらに考えます。
不変量を使う(その2)
不変量としてはその他にも、ポリオミノの辺や頂点や内角に注目していろいろなものを考えることができます。
試行錯誤の結果、次のようなものを考えてみることにしました。
まず縦縞、横縞にチェス盤の模様を塗り替えて、そこにポリオミノを配置します。
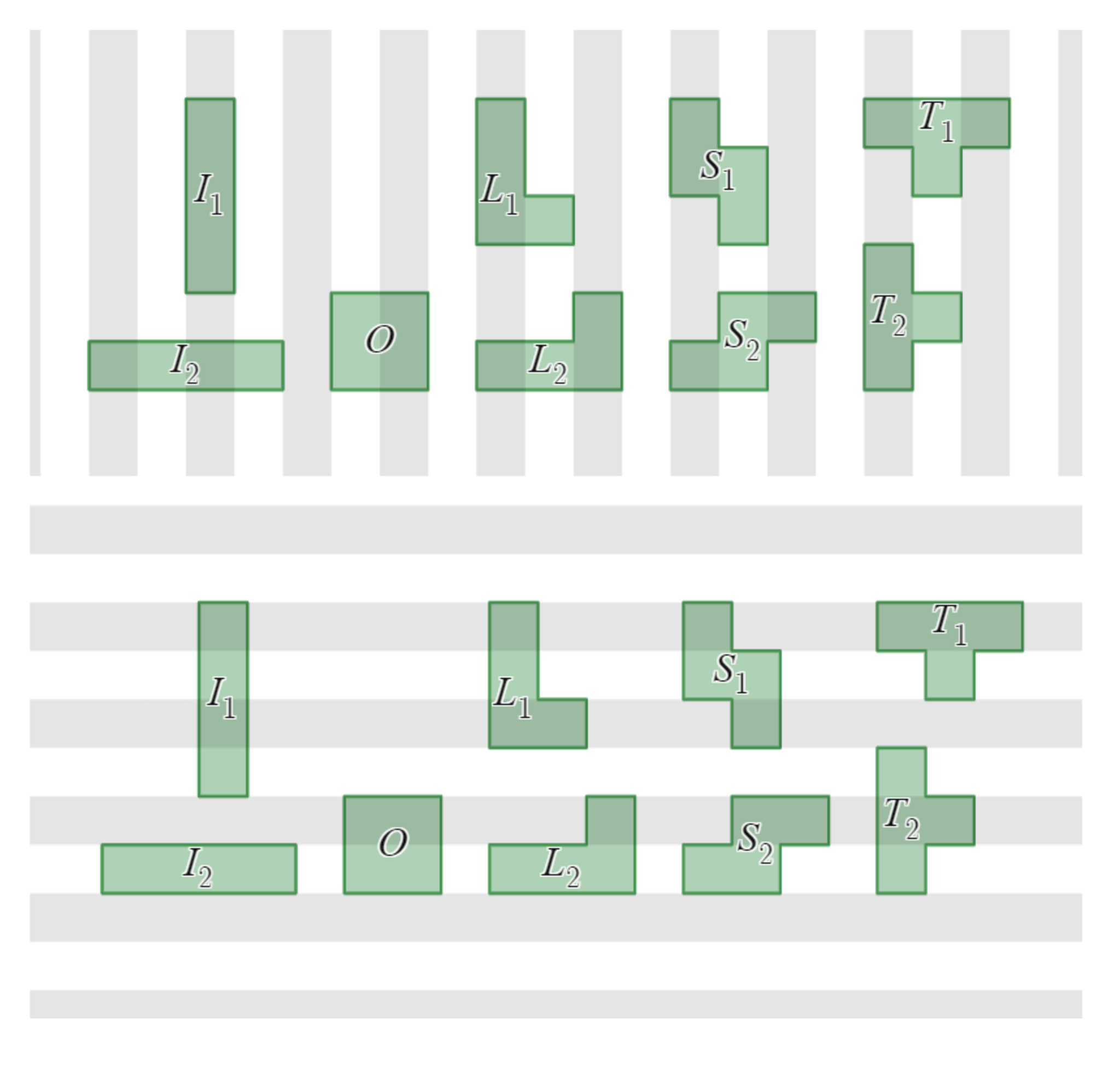縦縞の黒白差と、横縞の黒白差
縦縞の上にポリオミノを置いたときの「黒マスの数と白マスの数の差」を $a$、横縞の上にポリオミノを置いたときの「黒マスの数と白マスの数の差」を $b$ とします。
盤上に配置したポリオミノ $x$ に対する $a,b$ の組合せを $M[x]=[a,b]$ であらわすことにします。
$[a,b]$ は平行移動・裏返しに対して不変です。しかし、$90$ 度回転すると $a,b$ の値が入れ替わります。
そこで、テトロミノを$90$度回転したものを区別するため、上図のように $I,L,S,T$ は添え字をつけて $I_1,I_2,L_1,L_2,S_1,S_2,T_1,T_2$ として$2$種類を区別することにします。
各テトロミノについて表にすると次のとおり。
| $M[I_1],M[I_2]$ | $M[O]$ | $M[L_1],M[L_2]$ | $M[S_1],M[S_2]$ | $M[T_1],M[T_2]$ |
|---|---|---|---|---|
| $[4,0],[0,4]$ | $[0,0]$ | $[2,2],[2,2]$ | $[0,0],[0,0]$ | $[0,2],[2,0]$ |
もう少しシンプルにすることができそうです。 $[a,b]$ のカッコ内を降順に並べ替えて一意にしたものを$M\langle x\rangle=\langle c,d\rangle$のように書くことにします。
表にすると
| $M\langle I\rangle$ | $M\langle O\rangle$ | $M\langle L\rangle$ | $M\langle S\rangle$ | $M\langle T\rangle$ |
|---|---|---|---|---|
| $\langle 4,0\rangle$ | $\langle 0,0\rangle$ | $\langle 2,2\rangle$ | $\langle 0,0\rangle$ | $\langle 2,0\rangle$ |
$M\langle x\rangle$ はポリオミノ $x$ に対する不変量となっています。
注意
ここからは、$M[x]$ と $M\langle x\rangle$ が記事の中に混在してちょっと読みにくいかもしれません(すいません)。
$M[x]$ は「$[\text{縦},\text{横}]$の順番がある方」、 $M\langle x\rangle$ は「順番がない方」と思っていただければわかりやすいかと思います。
しばらくは、主に $M[x]$ ($[\text{縦},\text{横}]$の順番がある方)を使って議論していきます。
偶数ミノ、奇数ミノとの関係
ここで、$M[\text{偶数ミノ}]$ や $M[\text{奇数ミノ}]$ について、次が成り立つことを確認しておきます。
$M[\text{偶数ミノ}]=[\text{偶数},\text{偶数}]$
$M[\text{奇数ミノ}]=[\text{奇数},\text{奇数}]$
偶数を２つの整数に分けるとその偶奇が一致するから、その２つに分けた整数の差は偶数となる。
また、奇数を２つの整数に分けるとその偶奇は一致しないから、その２つに分けた整数の差も奇数となる。
ポリオミノの「引き算」との関係
次に、ポリオミノの「引き算」をすると、$M[x]$ がどのように変化するか考えてみましょう。
$M[x]=[a,b],M[y]=[c,d]$ とします。ポリオミノ$x$ からポリオミノ $y$ を削ってできるポリオミノを「$x-y$」で表すと、
$M[x-y]=\left[|a \pm c|,|b \pm d|\right]$
※ 複号は$x,y$により定まる
となります。
複号になっているのは、$a,b,c,d$ のそれぞれが「黒マスの数 － 白マスの数」と「白マスの数 － 黒マスの数」の どちらになっているかで式が変化するためです。
具体例で考える
今、ポリオミノ$x$ からポリオミノ $y$ を削ると $I_1$テトロミノができ、ポリオミノ$y$ の位置や向きを変えたポリオミノ$y'$ を削ると $O$テトロミノができたとします。
(※ ここでいろいろなテトロミノの中から $I_1$テトロミノと$O$テトロミノを選択したのにはちゃんと理由があります。読み進めていただければその理由がわかりますのでとりあえず「なぜこの組合せなのか」は気にしないでください。)
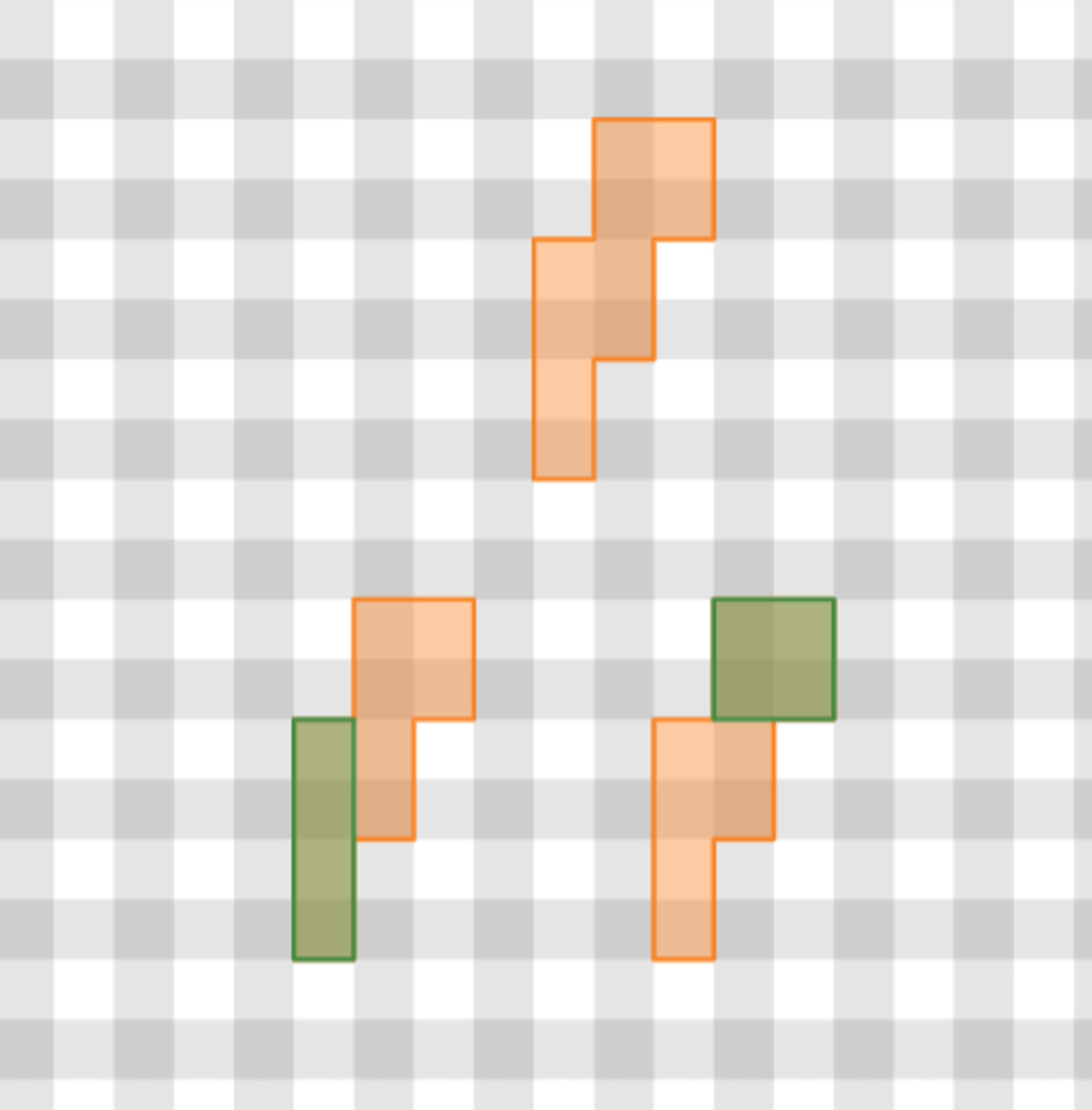I_1テトロミノとOテトロミノを削り出すポリオミノの例
このとき、
$M[x]=[a,b],M[y]=[c,d]$
だったととすると、
$M[y']=[c,d]\,\text{又は}\,[d,c]$
となります。
そこで場合分けして考えます。。
$M[y']=[c,d]$ の場合
${\displaystyle
\begin{cases}
M[x-y]=\left[|a \pm c|,|b \pm d|\right]\\
M[x-y']=\left[|a \pm c|,|b \pm d|\right]\\
M[I_1]=[4,0]\\
M[O]=[0,0]
\end{cases}
}$
を使って式を立てると
${\displaystyle \begin{cases} |a \pm c| = 4\\ |a \pm c| = 0\\ |b \pm d| = 0\\ |b \pm d| = 0 \end{cases} }$
これらすべてを満たす必要があります。($a,b,c,d$ は非負整数)
前半$2$行の複号が一致すると解なし。複号が異なる場合は第$2$行より$a=c$ となりこれを第$1$行に代入して$|2a|=4$ より$(a,c)=(2,2)$
補題$3$より、$x,y$ が偶数ミノでなければならないことがわかります。
$M[y']=[d,c]$ の場合
${\displaystyle
\begin{cases}
M[x-y]=\left[|a \pm c|,|b \pm d|\right]\\
M[x-y']=\left[|a \pm d|,|b \pm c|\right]\\
M[I_1]=[4,0]\\
M[O]=[0,0]
\end{cases}
}$
を使って式を立てると
${\displaystyle \begin{cases} |a \pm c| = 4\\ |a \pm d| = 0\\ |b \pm d| = 0\\ |b \pm c| = 0 \end{cases} }$
これらすべてを満たす必要があります。($a,b,c,d$ は非負整数)
下$3$行 より$a=b=c=d$ がわかり、第$1$行に代入すると $a=b=c=d=2$ となります。
したがって、補題 $3$ より $x,y$ が偶数ミノでなければならないことがわかります。
その$2$ まとめ
ここまでで、$I_1$テトロミノと、$O$テトロミノをどちらも削り出せるポリオミノの組合せは、どちらも偶数ミノでなければならないことがわかりました。
$M\langle I_2\rangle=M\langle I_1\rangle=\langle 4,0\rangle$
$M\langle S\rangle=M\langle O\rangle=\langle 0,0\rangle$
ですから、「$I_2$テトロミノと$O$テトロミノ」とか、「$I$テトロミノと$S$テトロミノ」についても全く同じ議論ができます。
まとめると、結局、次のことがわかったことになります。
『$I$テトロミノ』と、『$O$テトロミノ 又は $S$テトロミノ』をどちらも削り出せるポリオミノの組合せは、どちらも偶数ミノでなければならない
解答と追加問題
これで、この問題の答えができました!
(解答)
引き算でテトロミノ5種を作ることができるようなポリオミノの組は存在しない。
$T$テトロミノと、$T$以外のテトロミノをどちらも削り出せるポリオミノの組合せは、「奇数ミノと奇数ミノ」でなければならない(定理$2$より)
『$I$テトロミノ』と、『$O$テトロミノ 又は $S$テトロミノ』をどちらも削り出せるポリオミノの組合せは、どちらも偶数ミノでなければならない(定理$4$より)
したがって、引き算でテトロミノ $5$ 種を作ることができるようなポリオミノの組は存在しない。
ついに答えが出ました!
「条件を満たすポリオミノの組合せは存在しない」!
めでたしめでたし。
……
……
……のはずだったのですが。
みよしじゅんいち (@nosiika)さんから衝撃の追加問題が。
まだ十分理解できてはいないのですが、パリティ違いのTを除外した、I、L、O、Sができる可能性はありそうな感じですか？
つまり、「$5$種全部は不可能だとしても、$I,O,L,S$ の $4$ 種に限定すれば削り出せるポリオミノの組合せはあるだろうか」ということです。
先ほどと同様に考えると、もしそのようなポリオミノの組合せ $x,y$ が存在するならば、
$M\langle x\rangle=M\langle y\rangle=\langle 4,2\rangle$
又は
$M\langle x\rangle=M\langle y\rangle=\langle 2,0\rangle$
でなければいけないことまではわかりますが、そのような $x,y$ は本当に存在するのでしょうか。
試行錯誤したところでは、おそらく「不可能」と予想しています……が、まだ証明はできていません。
おわりに
というわけで、私が主に日曜数学活動をしているTwitter上での成果の一部をまとめさせていただきました。
当初の問題には答えが出てスッキリしましたが、最後の追加問題はまだ答えが出いません。
よろしければ皆さんもいっしょに考えてみませんか?
「条件を満たすポリオミノの組合せを発見する」か「条件を満たすポリオミノの組合せが存在しないことを証明する」か、どちらのルートを進むべきかすらまだ予想できないホットな話題です。
特に期限もないので好きな時に好きなだけ考えられるのが日曜数学の醍醐味です。
これを読んだ皆さんも是非素敵な日曜数学ライフを送ってくださいね!
この記事の参考にした主なツイートたち
最後に、この記事の元ネタとなったツイートたちの一部をご紹介します。みよしじゅんいち (@nosiika)さん、Taichi AOKI (@aoki_taichi)さん、TokusiN (@toku51n)さんとのやり取りがなければこの記事はできませんでした。ありがとうございました!
Pペントミノからモノミノを引くと、テトロミノ5種のうち、Tテトロミノ、Lテトロミノ、Oテトロミノ、Sテトロミノの4種を作ることができる。引き算でテトロミノ5種を作ることができるようなポリオミノの組は存在するだろうか？
— みよしじゅんいち (@nosiika) October 31, 2022
実はこれだけで不可能性いえたりしませんかね。 https://t.co/pzumubkn6P
— Taichi AOKI (@aoki_taichi) October 31, 2022
チェス盤のようにテトロミノを黒白に塗り分けると、Tは黒白の差が２、I・O・L・Sは０。したがって、削る方を黒白に塗り分けたときの黒白の差は１でなければいけません。
— ａｐｕ (@apu_yokai) October 31, 2022
もしかしてOテトロミノとIテトロミノを削り出しでできるのはPっぽいヘキソミノからドミノを削ったときだけだったりしないかしら？ https://t.co/wF69kxozuq
— Taichi AOKI (@aoki_taichi) October 31, 2022
これに正方形の枠を追加するトリッキーな反例がありますね。
— TokusiN (@toku51n) October 31, 2022
おお、なるほど
— ａｐｕ (@apu_yokai) October 31, 2022
…可能なパターンは全部偶数ですね
偶数でなければ無理である事を証明できれば元の主張も証明できますが🤔
通勤時間にずっとこれ考えてだんだけど、OミノとIミノを削り出しできるのは偶数ミノを削ったときに限られる事を証明できた（と思う）
— ａｐｕ (@apu_yokai) November 9, 2022
Tミノとそれ以外の組み合わせは奇数ミノを削ったときに限られるので、全てのテトロミノを削り出せるようなポリオミノは存在しない https://t.co/OwJhmOLhXQ
OテトロミノとIテトロミノを削り出しでできるのは元となるポリオミノから偶数ミノを削ったときだけ
— ａｐｕ (@apu_yokai) November 9, 2022
凄まじく雑だけど伝われ…! https://t.co/OwJhmOLhXQ pic.twitter.com/pgYyueuNgD
まだ十分理解できてはいないのですが、パリティ違いのTを除外した、I、L、O、Sができる可能性はありそうな感じですか？
— みよしじゅんいち (@nosiika) November 9, 2022
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
