∞-groupoid は空間である ～Joyal の拡張定理の応用とその証明～
こんにちは、 るめなる です。今回は無限圏論の話を扱います。これは 圏論 Advent Calendar 2022 の 13 日目の記事です。
Grothendieck は Pursuing Stacks という文書において、 "$\infty$-groupoid" と "空間" は同じものであるという ホモトピー仮説（homotopy hypothesis）を提唱しました。この仮説は、 "$\infty$-groupoid" や "空間" という言葉が具体的にどのような対象を指しているのかによって、その意味する内容は変わってきます。
この記事では、 "$\infty$-groupoid" として「すべての射が同型である quasi-category」を、"空間" として「Kan 複体」を選び、ホモトピー仮説を証明します。 quasi-category は $(\infty, 1)$-category のモデルの 1 つであり、 $(\infty,1)$-category は（かなり曖昧な表現ですが）通常の圏の "（高次）ホモトピー版" のようなものです。射がすべて同型な圏を groupoid と呼ぶことから、このように "$\infty$-groupoid" を定義するのは妥当性があるでしょう。また、 Kan 複体 はホモトピー論において基本的な空間である CW 複体と（それらのなすモデル圏が幾何学的実現関手と特異複体関手によって互いに Quillen 同値となるという意味で）等価であることが知られています。quasi-category と Kan 複体はそれぞれ 1 章で定義します。以降、ホモトピー仮説というときには先程に述べた意味での $\infty$-groupoid と Kan 複体が等価であるということを指すことにします。
さて、ホモトピー仮説を示す際、本質的な役割を果たすのは Joyal の拡張定理（Joyal extension theorem）と呼ばれる定理です。簡単な議論によって、この定理からホモトピー仮説が導かれることがわかります（2 章）。本記事の主な目的は Joyal の拡張定理の証明を アイデア重視で 解説することです。
1 章 記法、用語
基本的な用語の定義をします。単体圏 $\Delta$、単体的集合とそれらのなす圏 $\sSet$、標準 $n$-単体 $\Delta^n$、boundary $\partial\Delta^n$、horn $\Horn{n}{i}$ の定義はここでは与えません。 Kerodon（
1.1.1
と
1.1.2
）や壱大整域（[3],
pdf のリンク
）を参照してください。
最初に記事を通して用いる技術的な用語を定義します。
$S = \Horn{n}{i}$ もしくは $S = \partial\Delta^n$ とし、$f : S \to X$ を $\sSet$ の射とする。このとき、$\sSet$ の射 $h : \Delta^n \to X$ で図式
$$
\xymatrix{
S \ar[r]^f \ar@{^{(}->}[d] & X \\
\Delta^n \ar@{-->}[ur]_h
}
$$
を可換にするものを、 $f$ の 拡張 とよぶ。
圏 $C$ における次の可換図式（$\mathrm{D}$）を考える：
$$
\xymatrix{
A \ar[r] \ar[d] & X \ar[d]\\
B \ar[r] & Y
}
$$
このとき、 $C$ の射 $h : B \to X$ であって次の図式を可換にするものを、可換図式（$\mathrm{D}$）の リフト という。
$$
\xymatrix{
A \ar[r] \ar[d] & X \ar[d]\\
B \ar@{-->}[ur]^h \ar[r] & Y
}
$$
$\infty$-category（quasi-category）とそれに関わる概念の定義を与えます。この記事では、便宜上、$\infty$-category に制限せず一般の単体的集合に対して対象や射を定義します。
単体的集合 $X$ が $\infty$-category であるとは、任意の $0 < i < n$ と $\sSet$ の射 $f : \Horn{n}{i} \to X$ に対し $f$ の拡張が存在すること、すなわちある $\sSet$ の射 $h : \Delta^n \to X$ が存在して、図式
$$ \xymatrix{ \Horn{n}{i} \ar[r]^f \ar@{^{(}->}[d] & X \\ \Delta^n \ar@{-->}[ur]_h } $$
が可換であることをいう（ Kerodon, 定義1.3.0.1. ）。
$X$ を単体的集合とする。
- $X$ の $0$-単体すべてのなす集合 $X_0$ の元を $X$ の 対象 という。
- $X$ の $1$-単体すべてのなす集合 $X_1$ の元を $X$ の 射 という。
- $X$ の射 $f$ に対し、$0$-単体 $a := d_1(f)$ を $f$ の ドメイン、$b := d_0(f)$ を $f$ の コドメイン といい、このとき $f : a \to b$ とかく。
（ Kerodon, 1.3.1 ）
$X$ を単体的集合とする。$X$ の射 $f: a \to b$ が 同型射 であるとは、ある $X$ の射 $g : b \to a$ が存在して、$\sSet$ の射 $\partial \Delta^2 \xrightarrow{(g,\ f,\ \mathrm{id}_a)} X$ と $\partial \Delta^2 \xrightarrow{(f,\ g,\ \mathrm{id}_b)} X$ の拡張が存在することをいう。
$$ \xymatrix{ a \ar[rr]^{\mathrm{id}_a} \ar[dr]_f & & a & b \ar[rr]^{\mathrm{id}_b} \ar[dr]_g & & b \\ & b \ar[ur]_g & & & a \ar[ur]_f & } $$
（ Kerodon, 1.3.6 ）
ホモトピー仮説の主役である $\infty$-groupoid と Kan 複体を定義しましょう。
任意の射が同型射である $\infty$-category $X$ を $\infty$-groupoid という。
単体的集合 $X$ が Kan 複体 であるとは、任意の $0 \leq i \leq n$ と $\sSet$ の射 $f : \Horn{n}{i} \to X$ に対し $f$ の拡張が存在すること、すなわちある $\sSet$ の射 $h : \Delta^n \to X$ が存在して、図式
$$ \xymatrix{ \Horn{n}{i} \ar[r]^f \ar@{^{(}->}[d] & X \\ \Delta^n \ar@{-->}[ur]_h } $$
が可換であることをいう（ Kerodon, 定義1.1.9.1. ）。
$\infty$-category と Kan 複体の違いは、前者は $0 < i < n$ のみに対する horn $f : \Horn{n}{i} \to X$（ inner horn ）が拡張を持つのに対し、後者は $i = 0,\ n$ に対する horn（ outer horn ）も拡張を持つという点です。特に、このことから Kan 複体は $\infty$-category であることがわかります。
2 章 $\infty$-groupoid と Kan 複体の等価性
示すべきこと
目標はホモトピー仮説、つまり $\infty$-groupoid と Kan 複体が同一のものであると示すことでした。正確にかくと次のようになります：
$\infty$-category $X$ に対して、次の 2 条件は同値である。
- $X$ は $\infty$-groupoid である。
- $X$は Kan 複体である。
(2)⇒(1) の方向は、Kan 複体の拡張の条件を駆使することで比較的かんたんにわかります。
- $X$ を Kan 複体とする。Kan 複体の定義の後に注意したように $X$ は $\infty$-category であるから、任意の $X$ における射 $\phi : a \to b$ が同型射であることを示せばよい。
- horn $\Horn{2}{0} \xrightarrow{(-,\ \mathrm{id}_a,\ \phi)} X$ を考える。
$$ \xymatrix{ a \ar[rr]^{\mathrm{id}_a} \ar[dr]_{\phi} & & a \\ & b } $$
仮定よりこれは拡張 $h : \Delta^2 \to X$ をもつ。$h$ を以下のように表す。
$$ \xymatrix{ a \ar[rr]^{\mathrm{id}_a} \ar[dr]_{\psi} & & a \\ & b \ar[ur]_{\psi} } $$ - $\psi$ が $\phi$ の逆射であることを示すため、もう 1 つ $2$-単体を作る必要がある（同型射の定義を参照）。これには horn $\Horn{3}{0} \xrightarrow{(-,\ s_0 \phi,\ s_1 \phi,\ h)} X$ を考えばよい（絵を描いてみよ）。この horn の拡張の $d_0$ をとって得られた $2$-単体が求めるものである。
したがって問題は (1)⇒(2) の方向を示すことです。$X$ を $\infty$-groupoid とし、少し議論してみます：
- 任意の $0 \leq i \leq n$ と $\sSet$ の射 $f : \Horn{n}{i} \to X$ に対し $f$ が拡張をもつことをいえばよいです。
- $X$ は $\infty$-category なので $0 < i < n$ に対しては成り立ちます。
- よって、任意の $n>0$ に対し、任意の $\sSet$ の射 $f : \Horn{n}{0} \to X$ と射 $g : \Horn{n}{n} \to X$ が拡張をもてばよいです。
- ここで、単体的集合の双対（ Kerodon, 1.3.2 ）を考えると、 $\Horn{n}{0}$ と $\Horn{n}{n}$ は互いに双対なので、 $f$ の形の射が拡張を持つことがいえれば $g$ についてもいえます。
- ゆえに、示すべきことは次のようにまとめられます：
$X$ を $\infty$-groupoid とする。このとき、任意の $n>0$ と $\sSet$ の射 $f : \Horn{n}{0} \to X$ に対し、$f$ は拡張 $h : \Delta^n \to X$ を持つ。
Joyal の拡張定理
さて、以上で主定理を証明するには命題 2 がいえればよいことがわかりました。実は、この命題 2 より強い結果が成り立ち、それを Joyal の拡張定理（Joyal extension theorem） といいます。
$X$ を $\infty$-category、 $n > 0$ とし、$f : \Horn{n}{0} \to X$ を $\sSet$ の射とする。$X$ の射 $\phi := f|_{\Delta^{\{0,1\}}}$ が同型射なら、 $f$ は拡張 $h: \Delta^n \to X$ を持つ。
この定理は、quasi-category の理論を大きく発展させた Joyal の 2002 年の論文 ``Quasi-categories and Kan complexes"（[5]）において、ホモトピー仮説とともに最初に示されました。
証明のイメージ
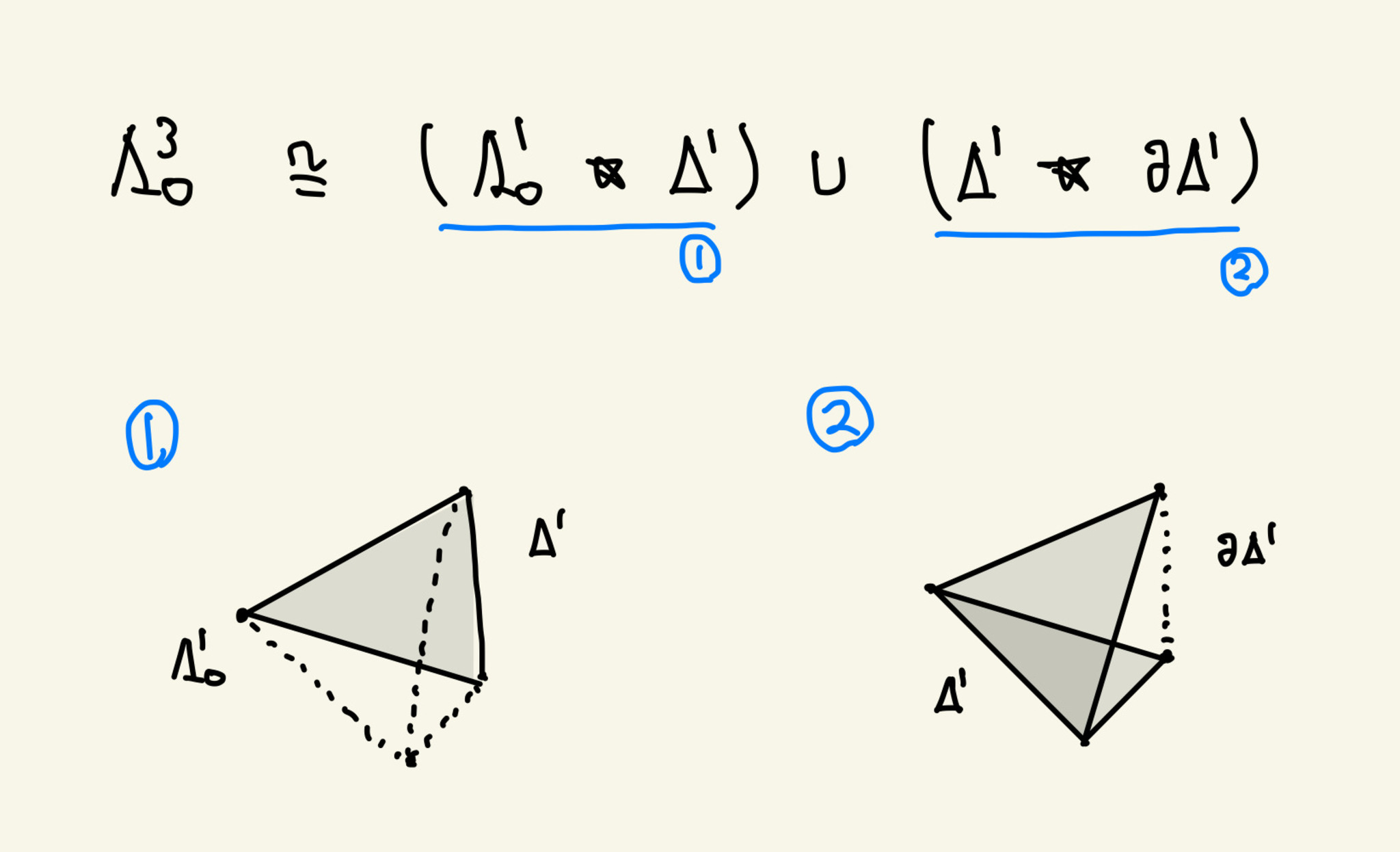
Joyal の拡張定理の証明のアイデアのイメージを説明します。簡単のために $n=3$ とします。つまり、 $\sSet$ の射 $f : \Horn{3}{0} \to X$ で $\phi := f|_{\Delta^{\{0,1\}}}$ が同型射であるものを $\Delta^3 \to X$ に拡張することを考えます。
射 $f$ を絵に描くと次のようになります：
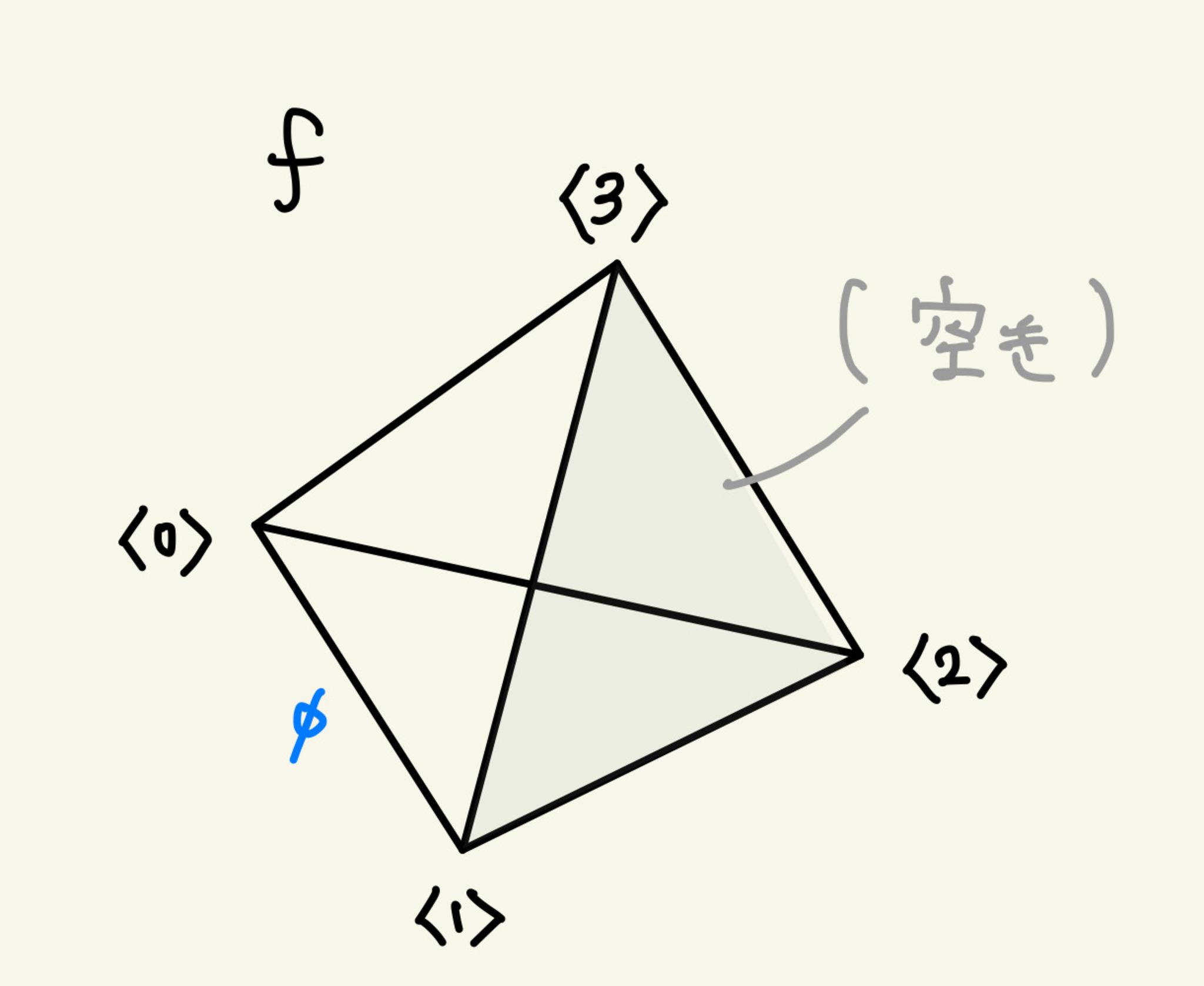射 f : Λ³₀ → X
$1$-単体 $\phi$ は頂点（$0$-単体）$\langle 0 \rangle$ から頂点 $\langle 1 \rangle$ への射 $\phi : \langle 0 \rangle \to \langle 1 \rangle$ です。 証明の（恐らく一番の）キーポイントは、この $\phi$ を $2$-単体 $\langle 023 \rangle$ から $2$-単体 $\langle 123 \rangle$ への射のようなものとみなすということです。
もう少し正確に述べます（3 章で注意するように完全に正確ではありません）： $\phi$ とそれを $1$-単体にもつ 2 つの $2$-単体 $\langle 012 \rangle,\ \langle 013 \rangle$ の "組" $(\phi,\ \langle 012 \rangle,\ \langle 013 \rangle)$ を、 $2$-単体 $\gamma := \simp{023}$ の境界 $\partial\gamma : \partial\Delta^2 \xrightarrow{(\simp{23},\ \simp{03},\ \simp{02})} X$ から $2$-単体 $\delta := \simp{123}$ の境界 $\partial\delta : \partial\Delta^2 \xrightarrow{(\simp{23},\ \simp{13},\ \simp{12})} X$ への "射" とみなす、ということが重要なアイデアです（注意： $f$ は horn $\Horn{3}{0}$ なので $2$-単体 $\delta$ は含まれません。説明のためにこのような書き方をしました）。
(φ, <012>, <013>) : ∂γ → ∂δ
さて、$\phi : \simp{0} \to \simp{1}$ は同型射なのでした。つまり $\phi$ の逆射 $\psi : \simp{1} \to \simp{0}$ が存在します。ここで、もし、 $\phi$ が "射" $(\phi,\ \simp{021},\ \simp{013}) : \partial\gamma \to \partial\delta$ として "同型射" であったらどうでしょうか？そのとき、"逆射 $(\psi,\ \rho_0,\ \rho_1) : \partial\delta \to \partial\gamma$" が存在するはずです。図にすると次のようになります：
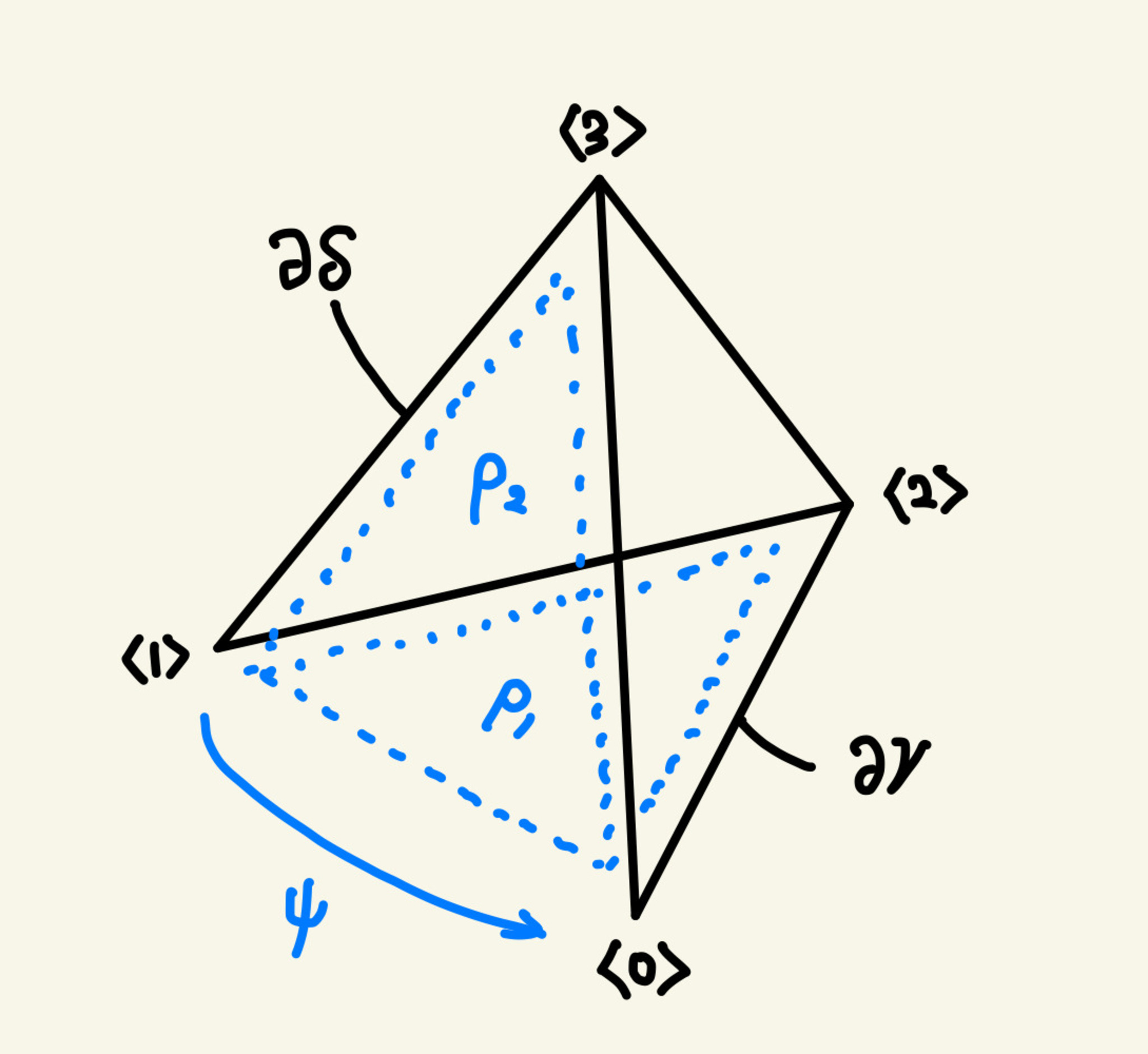(ψ, ρ₀, ρ₁) : ∂δ → ∂γ
考えていた horn は $\Horn{3}{0} \to X$ という形なので $2$-単体 $\gamma$ はもとの $f$ に備わっています。よって、上に描いた $(\psi,\ \rho_0,\ \rho_1)$ の $\partial\gamma$ の部分を "埋める" ことができそうです。すると、horn $\Horn{3}{1} \to X$ で $\delta$ の部分が空いたものができます。
これは inner horn です！$X$ は $\infty$-category なので、これの拡張 $k : \Delta^3 \to X$ は存在します。こうして $\partial\delta$ の中身を埋めることができました。ただ、$3$-単体 $k$ はもともとの $f$ を拡張した形にはなっていません。
そこでまたあのアイデアを使います。 $\partial\delta$ の中身を埋めている $2$-単体を $\delta'$ とかき、$3$-単体 $k$ を $2$-単体 $\delta'$ から $2$-単体 $\gamma$ への "射" $k : \delta' \to \gamma$ とみなします。
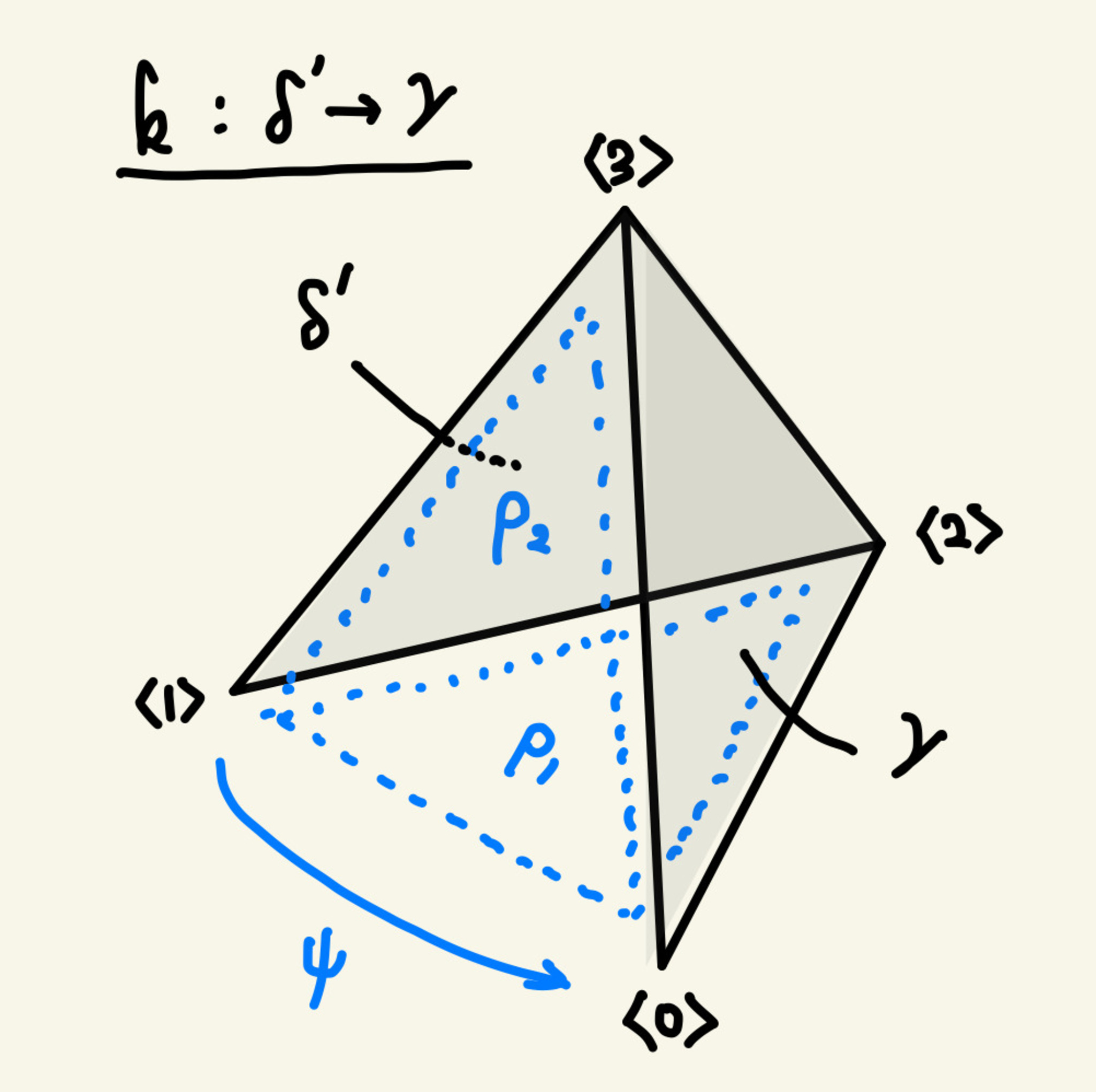k : δ' → γ
この "射" $k : \delta' \to \gamma$ は上に述べた射 $(\psi,\ \rho_0,\ \rho_1) : \partial\delta \to \partial\gamma$ をある意味で "拡張" したようなものと思えそうです。すると、$(\psi,\ \rho_0,\ \rho_1)$ が "同型射" だったので $k$ も "同型射" になりそうです。 実際にそうなることがわかり、このことから $k$ の "逆射" $h : \gamma \to \delta'$ の存在がいえます。 $k$ がそうであるように、 $h$ は $3$-単体 $h : \Delta^3 \to X$ になります。
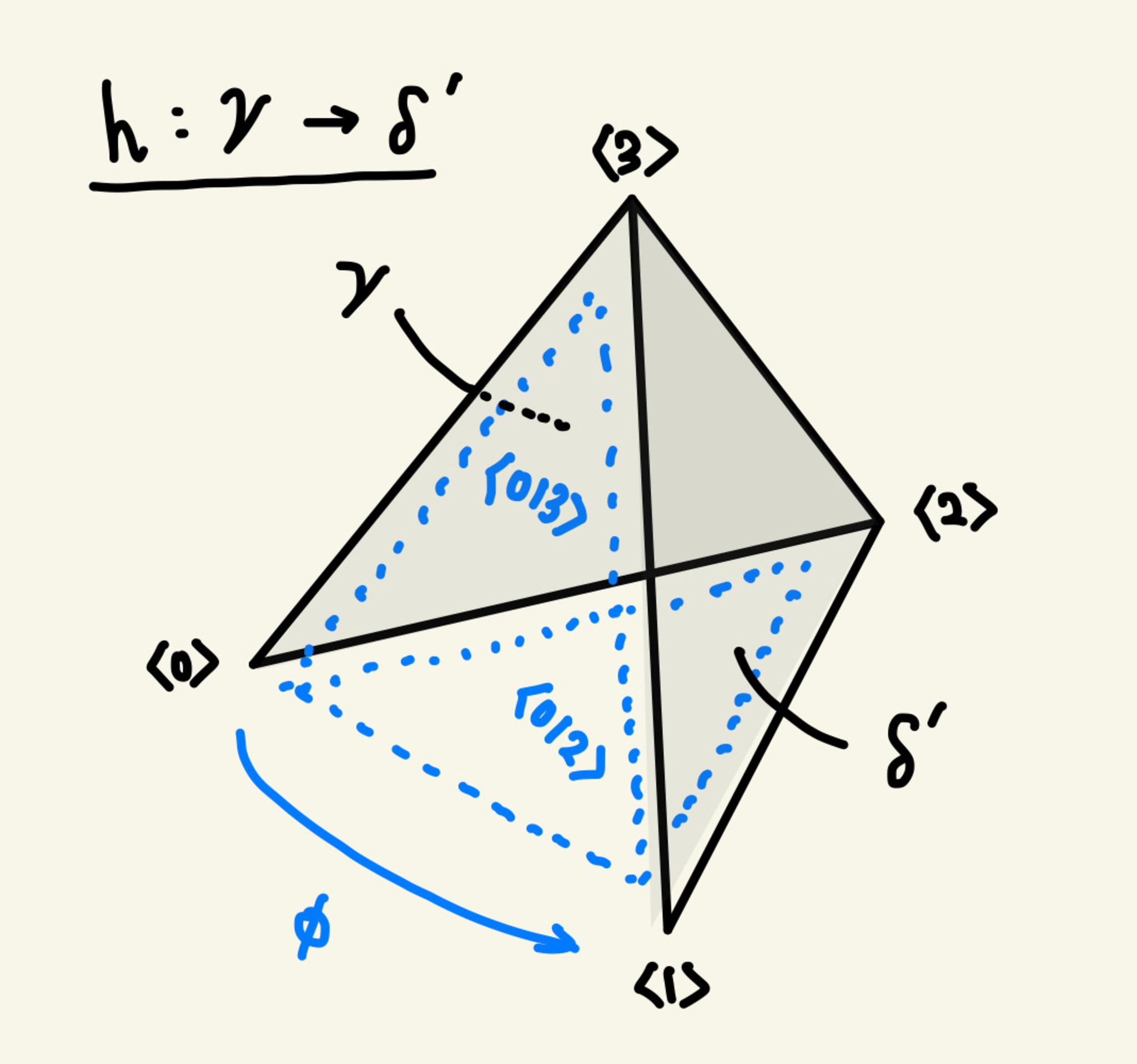h : γ → δ'
図から推測されるように、こうして得られた $3$-単体 $h : \Delta^3 \to X$ は求めていた $f$ の拡張になります！
以上が Joyal の拡張定理のアイデアと証明の流れのイメージになります。以降、これらのアイデアを正当化していきます。
Step1：組 $(\phi,\ \langle 012 \rangle,\ \langle 013 \rangle)$ や $3$-単体 $k : \Delta^3 \to X$ を射 $(\phi,\ \simp{021},\ \simp{013}) : \partial\gamma \to \partial\delta$ や $k : \delta' \to \gamma$ とみなすには 単体的集合のスライス という道具を使います。スライスの構成には 単体的集合の join という構成を用いるため、はじめにこれを説明します。
Step2： $\phi$ が同型射であることから射 $(\phi,\ \simp{021},\ \simp{013})$ が同型射であること、そして射 $(\psi,\ \rho_0,\ \rho_1)$ が同型射であることから射 $k$ が同型射であることを導く部分を正当化するためには right fibration という概念とその性質を利用します。ある 1 つの命題の証明は長くなってしまうため省略しています。
これらの準備のうえで、最後に上で述べた証明を厳密なものにしていきます。
3 章 アイデアの正当化
単体的集合の join
単体的集合の join を定義するために、まず圏の join を定義します。
$A, B$ を圏とする。このとき、圏 $A \star B$ を次のように定義し、$A$ と $B$ の join という。
- 対象全体の集まりを $\mathrm{Ob}(A\star B) := \mathrm{Ob}(A) \amalg \mathrm{Ob}(B)$ とする。
- 射全体の集まりを $\mathrm{Mor}(A\star B) := \mathrm{Mor}(A) \amalg (\mathrm{Ob}(A)\times \mathrm{Ob}(B)) \amalg \mathrm{Mor}(B)$ とする。
- 対象 $x, y \in A\star B$ に対して
$$ \mathrm{Hom}_{A\star B}(x,y) = \begin{cases} \mathrm{Hom}_A(x,y) & (x, y \in \mathrm{Ob}(A)) \\ \mathrm{Hom}_B(x,y) & (x, y \in \mathrm{Ob}(B)) \\ \{*\} & (x \in \mathrm{Ob}(A),\ y \in \mathrm{Ob}(B)) \\ \emptyset & (x \in \mathrm{Ob}(B),\ y \in \mathrm{Ob}(A)) \end{cases} $$
とする。
これは実際に圏をなす（省略）。
単体圏 $\Delta$ に対象 $[-1] := \emptyset$ を追加してできた圏を $\Delta_+$ とかきます。このとき、対象 $[m], [n] \in \Delta_+$ に対して、これらは順序集合なので、圏とみなせば $[m]\star [n] = [m+n+1]$ が成り立ちます。
また、 $\Delta_+$ の射 $\alpha : [m] \to [n_1]\star [n_2]$ に対し、2 つの射 $\alpha_1 : [m_1] \to [n_1],\ \alpha_2 : [m_2] \to [n_2]$ が一意に存在して、 $\alpha = \alpha_1 \star \alpha_2$ が成り立ちます（もし $\alpha([m]) \subseteq [n_1]$ となるなら $m_2 = -1$ です）。これは組合せ論的な考察で簡単に示すことができます（省略）。
それでは、単体的集合の join を定義しましょう：
$X, Y$ を単体的集合とする。このとき、単体的集合 $X\star Y$ を次のように定義し、 $X$ と $Y$ の join という。
- 各 $n \geq 0$ に対し
$$ (X\star Y)_n := \coprod_{\substack{[n] = [n_1]\star [n_2] \\ [n_1],\ [n_2] \in \Delta_+}} X_{n_1} \times Y_{n_2} $$
と定める。 - $\Delta$ の射 $\alpha: [m] \to [n]$ に対し写像 $(X\star Y)(\alpha) : (X \star Y)_n \to (X \star Y)_m$ を次のように定める：任意の $(x,y) \in X_{n_1}\times Y_{n_2} \subseteq (X\star Y)_n$ に対し、 $\alpha$ を $\Delta_+$ の 2 つの射 $\alpha_1 : [m_1] \to [n_1],\ \alpha_2 : [m_2] \to [n_2]$ に $\alpha = \alpha_1 \star \alpha_2$ と分解する（上の記述を参照）。このとき、
$$ (X\star Y)(\alpha)((x,y)) := (X\alpha_1(x), Y\alpha_2(y)) \in X_{m_1}\times Y_{m_2} \subseteq (X\star Y)_m $$
とする。
標準 $n$-単体や horn、boundary など具体的な単体的集合同士の join を扱う際に便利なのが次の補題です。証明は join の定義から簡単にできます（[3], 命題 3 を利用します）。
$X, Y$ を単体的集合とし、それぞれ $A \subset X_m,\ B \subset Y_n$ （$m,n \geq 0$）で生成されているとする。 このとき、単体的集合 $X \star Y$ は $A \times B \subset X_m \times Y_n \subset (X \star Y)_{m+n+1}$ により生成される。
さて、Joyal の拡張定理の証明において重要になるのは次の同型です（ Kerodon, 補題4.3.6.14 ）。
同型
$$
\Horn{n}{0} \cong (\Horn{1}{0} \star \Delta^{n-2}) \underset{\Horn{1}{0}\star \partial \Delta^{n-2}}{\coprod} (\Delta^1 \star \partial \Delta^{n-2})
$$
がある。すなわち、次の図式は pushout である。
$$
\xymatrix{
\Horn{1}{0} \star \partial\Delta^{n-2} \ar[r] \ar[d] & \Delta^1 \star \partial\Delta^{n-2} \ar[d]\\
\Horn{1}{0} \star \Delta^{n-2} \ar[r] & \Horn{n}{0}
}
$$
主張のイメージのために、この同型を $n=3$ の場合に絵に描くと次のようになります：
n = 3 の場合
Joyal の拡張定理の証明のイメージの節で述べた "射" $(\phi, \simp{012}, \simp{013})$ が $\Delta^1 \star \partial\Delta^1$ の部分に、2-単体 $\gamma = \simp{023}$ が $\Horn{1}{0} \star \Delta^1$ の部分に対応しています！
（pushout の四角の成立）
- まず、定理の四角の図式が可換になるように射 $i^1 : \Horn{1}{0} \star \Delta^{n-2} \to \Horn{n}{0}$ と $i^2 : \Delta^1 \star \partial\Delta^{n-2} \to \Horn{n}{0}$ を定義する。
- 補題 4（と [3], 命題 4）より、
- $i^1$ の場合は写像 $i^1_{n-1} : (\Horn{1}{0} \star \Delta^{n-2})_{n-1} \to (\Horn{n}{0})_{n-1}$ による ${(\delta_1^1, \mathrm{id}{[n-2]})} \subset (\Horn{1}{0})_0 \times \Delta^{n-2}{n-2} \subset (\Horn{1}{0}\star \Delta^{n-2})_{n-1}$ の元の行き先を定めればよく、
- $i^2$ の場合は写像 $i^2_{n-1} :(\Delta^1 \star \partial\Delta^{n-2})_{n-1} \to (\Horn{n}{0})_{n-1}$ による ${(\mathrm{id}{[n-2]}, \delta_0^{n-2}),\ldots,(\mathrm{id}{[n-2]}, \delta_{n-2}^{n-2})} \subset \Delta^1_1 \times \partial\Delta^{n-2}{n-1} \subset (\Delta^1 \star \partial\Delta^{n-2}){n-1}$ の各元の行き先を定めればよい。
- 上でしたように $n=3$ や $n=4$ で絵を描くとどのように定めればよいか検討がつく。すると、
\begin{align*} &i^1_{n-1}((\delta_1^1, \mathrm{id}_{[n-2]})) := \delta_1^{n-1} \\ &i^2_{n-1}((\mathrm{id}_{[n-2]}, \delta_i^{n-2})) := \delta_{i+2}^{n-2} && (0 \leq i \leq n-2) \end{align*}
と定めればうまくいくことが予想される。 -
- と同じように $\Horn{1}{0} \star \partial\Delta^{n-2}$ はそのある $(n-2)$-単体の集合で生成される。よって、詳細は省略するが、この集合の各元の行き先をみれば、実際に定理の図式が可換となることがわかる。
（pushout であることの証明）
$\Horn{n}{0}$ が pushout の普遍性をもつことを示せばよい。すなわち、任意の可換図式
$$
\xymatrix{
\Horn{1}{0}\star \partial\Delta^{n-2} \ar[r]\ar[d] & \Delta^1 \star \partial\Delta^{n-2} \ar[d] \\
\Horn{1}{0} \star \Delta^{n-2} \ar[r] & X
}
$$
に対し、ある射 $f : \Horn{n}{0} \to X$ が一意的に存在して、図式（＊）
\begin{align}
\xymatrix{
\Horn{1}{0}\star \partial\Delta^{n-2} \ar[r]\ar[d] & \Delta^1 \star \partial\Delta^{n-2} \ar[d] \ar@/^16pt/[ddr] & \\
\Horn{1}{0} \star \Delta^{n-2} \ar[r] \ar@/_16pt/[drr] & \Horn{n}{0} \ar[dr]^{f} & \\
& & X
}
\end{align}
が可換になればよい。
- 射 $\Horn{1}{0}\star \Delta^{n-2} \to X$ の行き先は $(n-1)$-単体の集合 $\{(\delta_1^1, \mathrm{id}_{[n-2]})\} \subset (\Horn{1}{0}\star \Delta^{n-2})_{n-1}$ の元の行き先 $x \in X_{n-1}$ で決定され、射 $\Delta^1 \star \partial\Delta^{n-2} \to X$ は $(n-1)$-単体の集合 $\{(\mathrm{id}_{[n-2]}, \delta_0^{n-2}),\ldots,(\mathrm{id}_{[n-2]}, \delta_{n-2}^{n-2})\} \subset (\Delta^1 \star \partial\Delta^{n-2})_{n-1}$ の各元の行き先 $y_0,\ldots,y_{n-2} \in X_{n-1}$ で決定される。
- 証明の前半の 2. と同じようにして、$(n-1)$-単体 $x, y_0, \ldots, y_{n-2}$ から射 $f : \Horn{n}{0} \xrightarrow{(-,x,y_0,\ldots,y_{n-2})} X$ を定義すると、図式（＊）が可換になることがわかる。また、生成元の行き先で射が一意に定まることから、一意性もいえる。
単体的集合のスライス
目的の、単体的集合のスライスを定義します。
$p : S \to X$ を $\sSet$ の射とする。このとき、単体的集合 $X_{/p}$ を次のように定義し、 $p$ 上の $X$ の スライス単体的集合（slice simplicial set）という。
各 $n\geq 0$ に対し、 $(X_{/p})_n := \mathrm{Hom}_p(\Delta^n \star S, X) := \{\ \sigma : \Delta^n \star S \to X \mid \sigma|_{S} = p\ \}$ と定める。
$$ \xymatrix{ S \ar[d]\ar[r]^p & X \\ \Delta^n \star S \ar@{-->}[ur]_\sigma } $$$\Delta$ の射 $\alpha: [m] \to [n]$ に対し写像 $(X_{/p})(\alpha) : (X_{/p})_n \to (X_{/p})_m$ を、射 $\Delta^m \star S \xrightarrow{\alpha \star \mathrm{id}_S} \Delta^n \star S$ との合成によって定める。
スライス単体的集合について、次の重要な事実が成り立ちます（ Kerodon, 命題4.3.5.13. ）。
$p : S \to X$ を $\sSet$ の射とする。このとき、任意の単体的集合 $K \in \sSet$ に対して、集合の同型 $\Hom_\sSet(K, X_{/p}) \cong \Hom_p(K\star S, X)$ がある。
双方向の写像を定義して地道に全単射を示す方法もあります（今後別記事で書くかもしれません）。多くの場合、任意の単体的集合 $S$ に対し関手 $-\star S : \sSet \to \sSet$ が余極限を保つことと、任意の単体的集合 $K$ が $K \cong \underset{\Delta^n \to K}{\mathrm{colim}}\ \Delta^n$ とかけること（$\because$ 任意の前層は表現可能関手の余極限で表せる）を用いて、
\begin{align*}
\Hom_\sSet(K, X_{/p}) &\cong \underset{\Delta^n \to K}{\mathrm{colim}}\ \Hom_\sSet(\Delta^n, X_{/p}) \\
&=\underset{\Delta^n \to K}{\mathrm{colim}}\ \Hom_p(\Delta^n \star S, X) \\
&\cong \Hom_p(K\star S, X)
\end{align*}
と示します。
後ほど使う概念をここで定義しておきます。
$p : S \to X$ を $\sSet$ の射とする。このとき $\sSet$ の射 $q : X_{/p} \to X$ を、各 $n \geq 0$ に対して $(q_X)_n := (X_{/p})_n = \Hom_p(\Delta^n \star S, X) \ni \sigma \mapsto \sigma|_{\Delta^n} \in X_n$ として定義し、 忘却関手 と呼ぶ（ Kerodon, 注意4.5.3.2. ）。
$T \xrightarrow{j} S \xrightarrow{p} X$ を $\sSet$ の射とする。このとき、 $\sSet$ の射 $r : X_{/p} \to X_{/p\circ j}$ を、各 $n \geq 0$ に対して合成 $\Delta^n \star T \xrightarrow{\mathrm{id}\star j} \Delta^n \star S \xrightarrow{} X$ を考えることで定め、 制限関手 という。
Step1 の正当化
再び $n=3$ とし、horn $f : \Horn{3}{0} \to X$ を考えます。命題 5 の同型を用いてこれを射 $f : (\Horn{1}{0} \star \Delta^{1})\amalg (\Delta^1 \star \partial\Delta^{1}) \to X$ と同一視します。そして、この射の第 1 成分への制限を $f^1 : \Horn{1}{0} \star \Delta^{1} \to X$、第 2 成分への制限を $f^2 : \Delta^1 \star \partial\Delta^{1} \to X$ とおきます。すなわち、次の図式が可換です：
\begin{align}
\xymatrix{
\Horn{1}{0}\star \partial\Delta^{1} \ar[r]\ar[d] & \Delta^1 \star \partial\Delta^{1} \ar[d] \ar@/^16pt/[ddr]^{f^2} & \\
\Horn{1}{0} \star \Delta^{1} \ar[r] \ar@/_16pt/[drr]_{f^1} & \Horn{3}{0} \ar[dr]^{f} & \\
& & X
}
\end{align}
また、 $\sigma := f^1|_{\Delta^1} : \Delta^1 \to X,\ \sigma_0 := f^2|_{\partial\Delta^1} : \partial\Delta^1 \to X$ とおきます。
$$
\xymatrix{
\Delta^1 \ar[d]\ar[r]^\sigma & X & & \partial\Delta^1 \ar[d]\ar[r]^{\sigma_0} & X\\
\Horn{1}{0} \star \Delta^1 \ar[ur]_{f^1} & & & \Delta^1 \star \partial\Delta^1 \ar[ur]_{f^2}
}
$$
ここで、命題 6 を用いると、
- 同型 $\Hom_\sigma(\Horn{1}{0} \star \Delta^1, X) \cong \Hom_\sSet(\Horn{1}{0}, X_{/\sigma})$ により $f^1$ から $\sSet$ の射 $g^1 : \Horn{1}{0} \to X_{/\sigma}$ が、
- 同型 $\Hom_{\sigma_0}(\Delta^1 \star \partial\Delta^1, X) \cong \Hom_\sSet(\Delta^1, X_{/\sigma_0})$ により $f^2$ から $\sSet$ の射 $g^2 : \Delta^1 \to X_{/\sigma_0}$ が
一意に定まります。
命題 5 の直後に述べたことを踏まえると、2 章の説明での "射" $(\phi, \simp{012}, \simp{013})$ は、$X_{/\sigma_0}$ という単体的集合における、上のように定まる 本当の $1$-単体 $g^2 : \Delta^1 \to X_{/\sigma_0}$ に対応しているとわかります！今回必要にならないので詳しくは説明しませんが、実は $X$ が $\infty$-category のとき $X_{/\sigma_0}$ も $\infty$-category になります。したがって、 $g^2$ は $X_{/\sigma_0}$ における射 $g^2 : d_1(g^2) \to d_0(g^2)$ です。
2 章の説明では、 "射" $(\phi, \simp{012}, \simp{013})$ を $2$-単体の boundary の間の射 $(\phi, \simp{012}, \simp{013}) : \partial\gamma \to \partial\delta$ とみなしました。しかし、上で定めた実際の射 $g^2$ は horn $\Horn{2}{0} \to X$ の間の射となります。つまり、 $X_{/\sigma_0}$ における 1-単体（対象）は horn $\Horn{2}{0} \to X$ と対応します。
このことは合成 $\Delta^0 \star \partial\Delta^1 \to \Delta^1 \star \partial\Delta^1 \xrightarrow{f^2} X$ と同型 $\Delta^0 \star \partial\Delta^1 \cong \Horn{2}{0}$ を考えることでわかります。
right fibration
以上で、単体的集合のスライスを用いることにより、$1$-単体とは限らない単体や horn、boundary などの間の "射" を定式化できることがわかりました。次に Step2 を定式化していきます。
2 章の議論では $\phi = f|_{\Delta^{\{0,1\}}} : \Delta^1 \to X$ が同型射であることから $g^2 : \Delta^1 \to X_{/\sigma_0}$ も同型射であるという予想を認めて議論を進めていました。
$\phi : \Delta^1 \to X$ が同型射なら、 $g^2 : \Delta^1 \to X_{/\sigma_0}$ も同型射である。
この予想は、2 セクション前で定義した忘却関手 $q : X_{/\sigma_0} \to X$ が right fibration になることと、その right fibration の性質を用いることで証明できます。まずは right fibration を定義します。
$p : X \to Y$ を $\sSet$ の射とする。このとき、 $p$ が right fibration であるとは、任意の $0 < i \leq n$ と任意の可換図式
$$
\xymatrix{
\Horn{n}{i} \ar[r] \ar@{^{(}->}[d] & X \ar[d]^p \\
\Delta^n \ar[r] & Y
}
$$
に対して、この図式がリフト $h: \Delta^n \to X$ を持つことをいう。
そして、今回は証明しませんが、 $X$ が $\infty$-category の場合、任意の忘却関手は right fibration になります！（ Kerodon, 命題4.3.6.1. ）
$p : S \to X$ を $\sSet$ の射とし、 $X$ を $\infty$-category とする。このとき、忘却関手 $q : X_{/p} \to X$ は right fibration である。
予想（1）を証明するのに使う right fibration の性質は次の命題です（ Kerodon, 命題4.4.2.11. ）。忘却関手 $q : X_{/\sigma_0} \to X$ を思い浮かべながら証明を追ってみるといいかもしれません。
$p : X \to Y$ を right fibration、$X$ を $\infty$-category、$\psi : \Delta^1 \to X$ を $X$ における射、 $\phi : \Delta^1 \to Y$ を $Y$ における同型射とする。もし $p(\psi) = \phi$ なら、すなわち図式
$$
\xymatrix{
\Delta^1 \ar[dr]_\phi \ar[r]^\psi & X \ar[d]^p \\
& Y
}
$$
が可換なら、 $\psi$ も同型射である。
$\psi$ は $X$ において $\psi : a \to b$ という形の射であるとする。仮定より $Y$ における射 $\phi = p(\psi) : p(a) \to p(b)$ には逆射 $\phi' : p(b) \to p(a)$ が存在する。
ということは、ある $2$-単体 $\omega : \Delta^2 \to X$ で次のようなものが存在する：
$$ \xymatrix{ p(b) \ar[rr]^{\mathrm{id}_{p(b)}} \ar[dr]_{\phi'} & & p(b) \\ & p(a) \ar[ur]_{p(\psi)} } $$すると、上の図からわかるように、次の図式が可換である：
$$ \xymatrix{ \Horn{2}{2} \ar[r]^{(\psi, \mathrm{id}_b, -)} \ar@{^{(}->}[d] & X \ar[d]^p \\ \Delta^2 \ar[r]_\omega & Y } $$$p$ は right fibration であるから、この可換図式のリフト $h : \Delta^2 \to X$ が存在する。
$$ \xymatrix{ \Horn{2}{2} \ar[r]^{(\psi, \mathrm{id}_b, -)} \ar@{^{(}->}[d] & X \ar[d]^p \\ \Delta^2 \ar[r]_\omega \ar@{-->}[ur]^h & Y } $$
$\psi' := h|_{\Delta^{\{0,1\}}}$ とおけば $h$ は次のような $2$-単体だから、 $\psi \circ \psi' \simeq \mathrm{id}_b$ がいえた。
$$ \xymatrix{ b \ar[rr]^{\mathrm{id}_b} \ar[dr]_{\psi'} & & b \\ & a \ar[ur]_{\psi} } $$あとは $\psi' \circ \psi \simeq \mathrm{id}_a$ ならよい。1 から 5 までの議論における $\phi$ を $\phi'$ に置き換えてもう一度行うことで、ある $X$ における射 $\psi'' : a \to b$ と、次のような $2$-単体 $h' : \Delta^2 \to X$ が存在するとわかる。
$$ \xymatrix{ a \ar[rr]^{\mathrm{id}_a} \ar[dr]_{\psi''} & & a \\ & b \ar[ur]_{\psi'} } $$$h$ と $h'$ から $\psi' \circ \psi \simeq \mathrm{id}_a$ を与える $2$-単体を作る。
まず horn $\Horn{3}{2} \xrightarrow{(h,\ s_0 \psi,\ -,\ h')} X$ の拡張が存在し、これの $d_2$ を $h'' : \Delta^2 \to X$ とする。
そして horn $\Horn{3}{1} \xrightarrow{(s_0 \psi',\ -,\ h',\ h'')} X$ の拡張の $d_1$ を考えると、これが求める $2$-単体であることがわかる。
上の証明の 6 は $\infty$-category の ホモトピー圏（ Kerodon, 1.3.5 参照）を考えれば簡単にわかる。すなわち： $[\psi] = [\psi] \circ ([\psi'] \circ [\psi'']) = ([\psi] \circ [\psi']) \circ [\psi''] = [\psi'']$ と $[\psi'] \circ [\psi''] = \mathrm{id}_a$ より $[\psi'] \circ [\psi] = \mathrm{id}_a$ となる。
ここまでくれば予想（１）は簡単に示せます。まず、図式
$$
\xymatrix{
\Delta^1 \ar[r]^{g^2} \ar[dr]_{\phi} & X_{/\sigma_0} \ar[d]^q \\
& X
}
$$
は可換です。これは、この図式が、次の図式に対応し、それが可換であることからわかります。
$$
\xymatrix{
\Delta^1 \star \partial\Delta^1 \ar[r]^{f^2} & X \\
\Delta^1 \ar[u] \ar[ur]_\phi &
}
$$
すると、命題 8 より $g^2 : \Delta^1 \to X_{/\sigma_0}$ が同型射であることがわかります！
上で忘却関手が right fibration であることを述べましたが、制限関手も部分集合への制限の場合には right fibration になります（ Kerodon, 系4.3.6.11. ）。これもここでは証明しません。
$p : S \to X$ を $\sSet$ の射、 $i : S_0 \hookrightarrow S$ を $S$ の部分単体的集合とし、$X$ を $\infty$-category とする。このとき、制限関手 $r : X_{/p} \to X_{/p\circ i}$ は right fibration である。
4 章 Joyal の拡張定理の証明（$n=3$の場合）
さて、この章では $n=3$ の場合に Joyal の拡張定理の証明の流れを追っていきます。2 章の議論と見比べてみてください。3 章「Step1 の正当化」の節の記号を使います。
"射" $(\phi,\ \simp{012},\ \simp{013}) : \partial\gamma \to \partial\delta$ を厳密に定式化したものが $g^2 : \Delta^1 \to X_{/\sigma_0}$ であること、 $\phi$ が $X$ における同型射であることから $g^2$ が $X_{/\sigma_0}$ における同型射であると導かれることは 3 章において述べました。次に進みましょう。
まず $g^2$ の逆射 $h^2 : \Delta^1 \to X_{/\sigma_0}$ を考えます。これは 2 章の議論における "射" $(\psi, \rho_0, \rho_1) : \partial\delta \to \partial\gamma$ にあたります。2 章ではこの $(\psi,\ \rho_0,\ \rho_1)$ の空き $\partial\gamma$ に $2$-単体 $\gamma$ を "埋める" ことで horn $\Horn{3}{1} \to X$ を構成したのでした。これを行います。次の図式 $(\rm A)$ を考えましょう：
$$
\xymatrix{
\Horn{1}{1} \star \partial\Delta^1 \ar[r] \ar[d] & \Delta^1 \star \partial\Delta^1 \ar[d]^{\widetilde{h^2}} \\
\Horn{1}{1} \star \Delta^1 \ar[r]_{f^1} & X
}
$$
ここで、$\widetilde{h^2} : \Delta^1 \star \partial\Delta^1 \to X$ は命題 6 により射 $h^2$ から得られる射であり、また同型 $\Horn{1}{1}\cong \Horn{1}{0}$ を用いて射 $f_1 : \Horn{1}{0} \star \Delta^1 \to X$ を $f_1 : \Horn{1}{1} \star \Delta^1 \to X$ と同一視しています（以降もこのような同一視を行います）。もし図式 $(\rm A)$ が可換なら、pushout（つまり "貼り合わせ"）を考えることにより、射
$$
l : \Horn{3}{1} \cong (\Horn{1}{1} \star \Delta^1) \underset{\Horn{1}{1} \star \partial\Delta^1}{\coprod} (\Delta^1 \star \partial\Delta^1) \xrightarrow{(f^1, \widetilde{h^2})} X
$$
が得られます！（最初の同型は命題 5 と同様にして得られます。）よって図式 $(\rm A)$ が可換であることを示せばよいです。
$h^2$ の定義より、 $(\Horn{1}{1}\star\partial\Delta^1 \to \Delta^1 \star \partial \Delta^1 \xrightarrow{\widetilde{h^2}} X)$ は $(\Horn{1}{0}\star\partial\Delta^1 \to \Delta^1 \star \partial\Delta^1 \xrightarrow{f^2} X)$ と同じです。よって、$f_1, f_2$ の定義、すなわち図式
$$
\xymatrix{
\Horn{1}{0} \star \partial\Delta^1 \ar[r] \ar[d] & \Delta^1 \star \partial\Delta^1 \ar[d]^{f^2} \\
\Horn{1}{0} \star \Delta^1 \ar[r]_{f^1} & X
}
$$
の可換性より、図式 $(\rm A)$ の可換性がわかります。
こうして horn $l: \Horn{3}{1} \to X$ が得られました。これは inner horn なので拡張 $k : \Delta^3 \to X$ が存在します。2 章の議論ではこの $k$ を "射" $k : \delta' \to \gamma$ とみなしていました。これを正当化するために同型 $\Delta^1 \star \Delta^1 \cong \Delta^3$ を使います。すると、例によって命題 6 より射 $\widetilde{k} : \Delta^1 \to X_{/\sigma}$ が得られます。
この $X_{/\sigma}$ における射 $\widetilde{k}$ の逆射があれば、それが元の $f$ の拡張であると考えられるのでした。そのため $\widetilde{k}$ が同型射だと示しましょう。それには、図式$(\rm B)$
$$
\xymatrix{
\Delta^1 \ar[r]^{\widetilde{k}} \ar[dr]_{h^2} & X_{/\sigma} \ar[d]^r \\
& X_{/\sigma_0}
}
$$
が可換であることを示し、 $r$ が right fibration であること（命題 9）と、命題 8 を使えばよいです。
図式 $(\rm B)$ の可換性は、join に書き直すと次の図式の可換性に対応します：
$$
\xymatrix{
\Delta^1 \star \Delta^1 \ar[r]^{k} & X \\
\Delta^1\star\partial\Delta^1 \ar[u] \ar[ur]_{\widetilde{h^2}} &
}
$$
この図式は、 $k$ が $l$ の拡張であることと $l$ の定義から可換性が簡単にわかります。よって、結局 $\widetilde{k}$ が同型射であること、つまり $\widetilde{k}$ の逆射 $\widetilde{h} : \Delta^1 \to X_{/\sigma}$ が存在することがいえました！
命題 6 よりこの $\widetilde{h}$ から射 $h : \Delta^3 \cong \Delta^1 \star \Delta^1 \to X$ が得られます。最後に、この $h$ が実際に $f$ の拡張であることを示しましょう。 $\widetilde{h}$ が $\widetilde{k}$ の $X_{/\sigma}$ における逆射であることと、 $k$ が $l$ の拡張であることから次の 2 つの図式が可換であることがわかります。
$$
\xymatrix{
\Horn{1}{0} \ar[r]^{g^1} \ar@{^{(}->}[d] & X_{/\sigma} & & & X_{/\sigma} \ar[d]^q \\
\Delta^1 \ar[ur]_{\widetilde{h}} & & & \Delta^1 \ar[r]_{g^2} \ar[ur]^{\widetilde{h}} & X_{/\sigma_0}
}
$$
これらの可換性は join に書き直すと次の図式の可換性に対応します。
$$
\xymatrix{
& \Delta^1 \star \partial\Delta^1 \ar[d] \ar@/^16pt/[rdd]^{f^2} & \\
\Horn{1}{0} \star \Delta^1 \ar[r] \ar@/_16pt/[drr]_{f^1} & \Delta^1 \star \Delta^1 \ar[dr]^h & \\
& & X
}
$$
したがって、次の 2 つの図式が可換であることになります。
$$
\xymatrix@=10pt{
\Horn{1}{0} \star \partial\Delta^1 \ar[r]\ar[d] & \Delta^1 \star \partial\Delta^1 \ar[d] \ar@/^8pt/[rdd] \ar@/^20pt/[rrddd]^{f^2} & & \\
\Horn{1}{0} \star \Delta^1 \ar[r] \ar@/_8pt/[drr] \ar@/_20pt/[ddrrr]_{f^1} & \Horn{3}{0} \ar[dr] & & \\
& & \Delta^1 \star \Delta^1 \ar[dr]^h & \\
& & & X
}
\xymatrix@=10pt{
\Horn{1}{0} \star \partial\Delta^1 \ar[r]\ar[d] & \Delta^1 \star \partial\Delta^1 \ar[d] \ar@/^18pt/[rrddd]^{f^2} & & \\
\Horn{1}{0} \star \Delta^1 \ar[r] \ar@/_18pt/[ddrrr]_{f^1} & \Horn{3}{0} \ar[ddrr]^f & & \\
& & \quad & \\
& & & X
}
$$
すると、pushout の普遍性より、次の図式が可換であること、すなわち $h$ が $f$ の拡張であることがわかります！
$$
\xymatrix{
\Horn{3}{0} \ar[r]^f \ar@{^{(}->}[d] & X \\
\Delta^3 \ar[ur]_h
}
$$
5 章 Joyal の拡張定理の証明（一般の場合）
以上の説明では、イメージの解説や概念・命題の導入と並行して証明を進めていったため議論が少しごちゃごちゃして見えたかもしれません。そこで、最後に、一般の場合での Joyal の拡張定理の証明を簡潔に書き下しておこうと思います。そのために、次の命題を使います（ Kerodon, 例4.4.1.10. ）。
$p : X \to Y$ を right fibration、$X$ を $\infty$-category、$a \in X_0$ とする。また、 $\phi : p(a) \to d$ を $Y$ における射、すなわち $\phi \in Y_1$ を次の図式が可換になるものであるとする：
$$
\xymatrix{
\Horn{1}{0} \ar[r]^a \ar@{^{(}->}[d] & X \ar[d]^p \\
\Delta^1 \ar[r]_\phi & Y
}
$$
このとき、 $\phi$ が同型射なら、ある $X$ における射 $\psi : a \to b$ が存在して $p(\psi) = \phi$ となる。すなわち、上の図式のリフト $\psi: \Delta^1 \to X$ が存在する（また、命題 8 より $\psi$ も同型射である）。
$\phi$ の逆射を $\phi' : d \to p(a)$ とする。
命題の図式の可換性から、次の図式は可換。
$$ \xymatrix{ \Horn{1}{1} \ar[r]^a \ar@{^{(}->}[d] & X \ar[d]^p \\ \Delta^1 \ar[r]_{\phi'} & Y } $$
すると、$p$ は right fibration だから、この図式のリフト $\psi' : \Delta^1 \to X$ が存在する。これを $\psi' : b \to a$ と表すことにする。1 より、次のような $X$ における $2$-単体 $\omega : \Delta^2 \to X$ が存在する。
$$ \xymatrix{ p(a) \ar[rr]^{\mathrm{id}_{p(a)}} \ar[dr]_{\phi} & & p(a) \\ & p(b) \ar[ur]_{p(\psi')} } $$
これは次の図式の可換性に言い換えられる。
$$ \xymatrix{ \Horn{2}{2} \ar[r]^{(\psi',\mathrm{id}_a,-)} \ar@{^{(}->}[d] & X \ar[d]^p \\ \Delta^2 \ar[r]_\omega & Y } $$$p$ は right fibration だから上の図式のリフト $h : \Delta^2 \to X$ が存在する。
$$ \xymatrix{ \Horn{2}{2} \ar[r]^{(\psi', \mathrm{id}_a, -)} \ar@{^{(}->}[d] & X \ar[d]^p \\ \Delta^2 \ar[r]_\omega \ar@{-->}[ur]^h & Y } $$
このとき、 $\psi := h|_{\Delta^{\{0,1\}}} : a \to b$ とおけば $p\circ h = \omega$ より $p(\psi) = \phi$ である。
それでは、Joyal の拡張定理の証明を述べます。
$f: \Horn{n}{0} \to X$ を horn、$\phi := f|_{\Delta^{\{0,1\}}}$ を同型射とする。
命題 5 の horn の分解を用いて、次の図式の可換性により射 $f_1, f_2$ を定義する。
\begin{align} \xymatrix{ \Horn{1}{0}\star \partial\Delta^{n-2} \ar[r]\ar[d] & \Delta^1 \star \partial\Delta^{n-2} \ar[d] \ar@/^16pt/[ddr]^{f^2} & \\ \Horn{1}{0} \star \Delta^{n-2} \ar[r] \ar@/_16pt/[drr]_{f^1} & \Horn{n}{0} \ar[dr]^{f} & \\ & & X } \end{align}
また、次の図式の可換性により射 $\sigma, \sigma_0$ を定義する。
$$ \xymatrix{ \Delta^{n-2} \ar[d]\ar[r]^\sigma & X & & \partial\Delta^{n-2} \ar[d]\ar[r]^{\sigma_0} & X\\ \Horn{1}{0} \star \Delta^{n-2} \ar[ur]_{f^1} & & & \Delta^1 \star \partial\Delta^{n-2} \ar[ur]_{f^2} } $$
ここで、 $\sigma_0 = (\partial\Delta^{n-2} \hookrightarrow \Delta^{n-2} \xrightarrow{\sigma} X)$ であることに注意する。join とスライスの対応（命題 6）により射 $f^2$ から射 $g^2 : \Delta^1 \to X_{/\sigma_0}$ が得られる。このとき、図式
$$ \xymatrix{ \Delta^1 \star \partial\Delta^{n-2} \ar[r]^{f^2} & X \\ \Delta^1 \ar[u] \ar[ur]_\phi & } $$
の可換性から、次の図式が可換であることがわかる。
$$ \xymatrix{ \Delta^1 \ar[r]^{g^2} \ar[dr]_{\phi} & X_{/\sigma_0} \ar[d]^q \\ & X } $$
ここで、 $q: X_{/\sigma_0} \to X$ は忘却関手である。よって、命題 8 より $g^2$ は $X_{/\sigma_0}$ における同型射となる。再び join とスライスの対応（命題 6）を使うと射 $f^1$ から射 $g^1 : \Horn{1}{0} \to X_{\sigma}$ が得られる。このとき、2 の最初の図式の外側をスライスに書き換えれば図式
$$ \xymatrix{ \Horn{1}{0} \ar[r]^{g^2} \ar@{^{(}->}[d] & X_{/\sigma} \ar[d]^r \\ \Delta^1 \ar[r]_{g^1} & X_{/\sigma_0} } $$
が可換であることがわかる。ここで、 $r: X_{/\sigma} \to X_{/\sigma_0}$ は制限関手である。すると、2 の最後で注意した事実より $r$ は right fibration であるから、3 と命題 10 より上の図式のリフト $\widetilde{h} : \Delta^1 \to X_{/\sigma}$ が存在する。
$$ \xymatrix{ \Horn{1}{0} \ar[r]^{g^2} \ar@{^{(}->}[d] & X_{/\sigma} \ar[d]^r \\ \Delta^1 \ar[r]_{g^1} \ar@{-->}[ur]^{\widetilde{h}}& X_{/\sigma_0} } $$上の図式を join に書き換えれば次の図式が可換であることがわかる。
$$ \xymatrix{ & \Delta^1 \star \partial\Delta^{n-2} \ar[d] \ar@/^16pt/[rdd]^{f^2} & \\ \Horn{1}{0} \star \Delta^{n-2} \ar[r] \ar@/_16pt/[drr]_{f^1} & \Delta^1 \star \Delta^{n-2} \ar[dr]^h & \\ & & X } $$
ここで、射 $h$ は join とスライスの対応（命題 6）より射 $\widetilde{h}$ から得られるものである。2 と 5 より次の 2 つの図式が可換である。
$$ \xymatrix@=10pt{ \Horn{1}{0} \star \partial\Delta^{n-2} \ar[r]\ar[d] & \Delta^1 \star \partial\Delta^{n-2} \ar[d] \ar@/^8pt/[rdd] \ar@/^20pt/[rrddd]^{f^2} & & \\ \Horn{1}{0} \star \Delta^{n-2} \ar[r] \ar@/_8pt/[drr] \ar@/_20pt/[ddrrr]_{f^1} & \Horn{n}{0} \ar[dr] & & \\ & & \Delta^1 \star \Delta^{n-2} \ar[dr]^h & \\ & & & X } \xymatrix@=10pt{ \Horn{1}{0} \star \partial\Delta^{n-2} \ar[r]\ar[d] & \Delta^1 \star \partial\Delta^{n-2} \ar[d] \ar@/^18pt/[rrddd]^{f^2} & & \\ \Horn{1}{0} \star \Delta^{n-2} \ar[r] \ar@/_18pt/[ddrrr]_{f^1} & \Horn{n}{0} \ar[ddrr]^f & & \\ & & \quad & \\ & & & X } $$
したがって、pushout の普遍性より図式
$$ \xymatrix{ \Horn{n}{0} \ar[r]^f \ar@{^{(}->}[d] & X \\ \Delta^1 \star \Delta^{n-2} \ar[d]_{\cong} \ar[ur] & \\ \Delta^n \ar[uur]_{h} } $$
は可換。すなわち、射 $h : \Delta^n \to X$ は $f$ の拡張である。
おわりに
この記事ではホモトピー仮説をテーマにして Joyal の拡張定理について解説してきました。単体的集合の join やスライスを利用することで、そのままでは複雑な図形の扱いを $\Horn{1}{0}$ や $\Delta^1$ など簡単な図形の操作に帰着でき、また実際に操作を行う際には忘却関手や制限関手が right fibration という性質をもつことが重要なのでした。これらの概念の重要性が伝われば嬉しいです。
（$\infty$-category の間の）忘却関手と制限関手が right fibration であることの証明は省略しました。これに関して今後記事を書きたいです。一応証明が載っている文献を挙げておきます：
- Kerodon [1], 4.3.6 Slices of $\infty$-Categories
- [2], 28. Slices of quasicategories
- [4], 2.1.1 Left Fibrations in Classical Category Theory
- Denis-Charles Cisinski, "Higher Categories and Higher Algebra", 3.4 Left or right fibrations, joins and slices, pdf のリンク
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
