次元定理についてのお話
Intro
はじめに
Nocturnalです.今回,karihito様の企画に参加するにあたり,人生で初めて記事を書かせていただきます.見にくい点もあろうかと思いますが,ご容赦下さい.
おそらくこの企画では,みなさん競技数学のことをいろいろと語られると思うので,私の記事では,線形代数について、特に私が最近学んで面白いと感じた次元定理についてお話ししたいと思います.
ただし,私自身も線形代数を深く学んだわけではないので,皆さんからのご意見などを是非お待ちしています.
また、行列式など煩雑な計算を要する物は扱いませんので、安心して下さい.
※線形代数を学んだことがある方にとっては,新鮮味がないように思われるかもしれないです.ご容赦下さい.
目次
この記事の終着点は,次元定理の証明です.
0.基本的な用語について
1.数ベクトル空間,線形写像
2.核,像とは
3.次元定理
基本的な事項
・m行n列(以下m×n)の行列$ \cdots $上下にm行,左右にn列並んだ行列
・n次正方行列$\cdots$n×n行列
・行列の掛け算
$ \begin{eqnarray}
\left(
\begin{array}{cc}
a_1&a_2\cdots a_n \\
\end{array}
\right)
\end{eqnarray} $$ \begin{eqnarray}
\left(
\begin{array}{cc}
b_1 \\
b_2\\
\vdots\\
b_n
\end{array}
\right)
\end{eqnarray}$$=a_1b_1+a_2b_2+\cdots+a_nb_n$
$A(m×n型)$,$B(n×l型)$をそれぞれ行ベクトル表示、列ベクトル表示して,
$\begin{eqnarray}
\left(
\begin{array}{cc}
a^1 \\
a^2\\
\vdots\\
a^m
\end{array}
\right)
\end{eqnarray}$$\begin{eqnarray}
\left(
\begin{array}{cc}
b^1 & b^2\cdots b^l \\
\end{array}
\right)
\end{eqnarray} $$=
\begin{eqnarray}
\left(
\begin{array}{cc}
a^1b^1\quad a^1b^2\cdots a^1b^l \\
a^2b^1 \quad a^2b^2\cdots a^2b^n\\
\vdots\\
a^mb^1 \quad a^mb^2\cdots a^mb^l\\
\end{array}
\right)
\end{eqnarray}$
※詳しくは他サイト参照
数ベクトル空間,線形写像
数ベクトル空間
数ベクトル空間とはずばり,世界です.
どういうことかというと,我々は今3次元の世界に暮らしていますね.結局私たちも3次元の数ベクトル空間に存在しています.座標平面だって,2次元の数ベクトル空間です.世界を一意的な方法で表したものが,数ベクトル空間のそれなのです...
さて,こんな適当な説明ではいけないような気もするので,ある程度しっかりとした定義を書いていきます.
数ベクトル空間とは,以下のような線形空間のことである.
実数全体の集合を$ \mathbb{R} $とする.
$ \mathbb{R} ^{n}=\lbrace \begin{eqnarray}
\left(
\begin{array}{cc}
a_1 \\
a_2\\
\vdots \\
a_n
\end{array}
\right)
| \hspace{10pt} a_1,a_2, \cdots,a_n \in \mathbb{R}
\end{eqnarray} \rbrace
$
又,$ \mathbb{R} $の部分が$ \mathbb{C} $などになってもよい.
*線形空間とは,簡単に言えばベクトルの足し引き,定数倍が可能であり,空間内で完結するものです.詳しくは他の文献を参考にして下さい.今回は,線形空間の厳密な定義については割愛します.
また,今後$V$上の部分空間というなどという言葉が出てきますが,$W \subset V$である線形空間$W$のことを指します.
上で見てもらえば分かりますが,xy平面は$ \mathbb{R} ^2$で,xyz空間は$ \mathbb{R} ^3$で表されます.
…ということは,$ \mathbb{R} ^4$は,4次元空間を表しているということになりますね.4次元という空間を,幾何学的描像として理解するのは全く容易ではないですが,ベクトル空間を使うことによって,簡単に理解することができます.
これってすごいロマンありますよね.
基底
ここで今後重要となる基底という概念を取り入れていきます.
基底は,簡単に言えば, 高校で習う単位ベクトルです.要は,そのベクトルをいい感じに組み合わせることで存在するベクトルすべてを作り出すことができる物です.これを定量的に表すとこのようになります.
ここからは$ \mathbb{R} $とか$ \mathbb{C} $とかのことをまとめて$K$と呼んでいきます.
$v_1, v_2 \cdots ,v_n \in V$とする($V$は$K$上のベクトル空間).
以下を満たす$v_1, v_2 \cdots ,v_n$を$V$の基底と呼ぶ.
・$v_1, v_2 \cdots ,v_n$は一次独立
・任意の$v\in V$に対し,ある$k_1, k_2 \cdots ,k_n \in K$が存在して,
$v=k_1v_1+k_2v_2+\cdots +k_nv_n$と表せる
また,あるベクトル空間の基底の個数は一意に定まる.この個数を次元と言い,$dim V$と表される.
ここで,$ \mathbb{R}^n $の基底は
$v_1= \begin{eqnarray}
\left(
\begin{array}{cc}
1 \\
0\\
\vdots \\
0
\end{array}
\right)
\end{eqnarray}$ $v_2= \begin{eqnarray}
\left(
\begin{array}{cc}
0 \\
1\\
\vdots \\
0
\end{array}
\right)
\end{eqnarray}$ $\cdots$ $v_n= \begin{eqnarray}
\left(
\begin{array}{cc}
0 \\
0\\
\vdots \\
1
\end{array}
\right)
\end{eqnarray}$
とすることができます.これを標準基底と呼びます.
さて,線形空間の話はこんなところにしておいて,線形写像の話にいきたいと思います.
線形写像
「写像ってなんすか?」でおなじみの写像ですが,その中にも線形写像という部類のものがあります.
そもそも写像というのは,あるものが入力されるとそれに伴ったあるものが出力されるという概念ですが,ある条件を満たすとそれが線形写像へとパワーアップします.
以下、写像を$f$と表します.
$V,W$は$K$上のベクトル空間である.$f:V \rightarrow W$が,次の条件を満たすとき,$f$は線形写像であるという.
・$f ( x + y ) = f(x) +f(y), \hspace{10pt} x,y \in V$
・$f(kx) = kf(x), \hspace{10pt} k\in K , \hspace{10pt} x\in V$
噛み砕いて言えば,
・$f: \mathbb{R} \rightarrow \mathbb{R}$ $f(x)=ax$は線形写像である.証明は容易であるため割愛.
・$f: \mathbb{R}^2 \rightarrow \mathbb{R}^2 $ $A= \begin{eqnarray}
\left(
\begin{array}{cc}
2 & 0 \\
3 & 1
\end{array}
\right)
\end{eqnarray}$とし,$f(x)=Ax$は線形写像である.これは行列において和の分配法則が成り立つことなどから示される.
では,これから線形写像の核や像についてお話ししたいと思います.
核,像
まず,こんな感じの図を見てもらうのが早いと思います.
 核
核
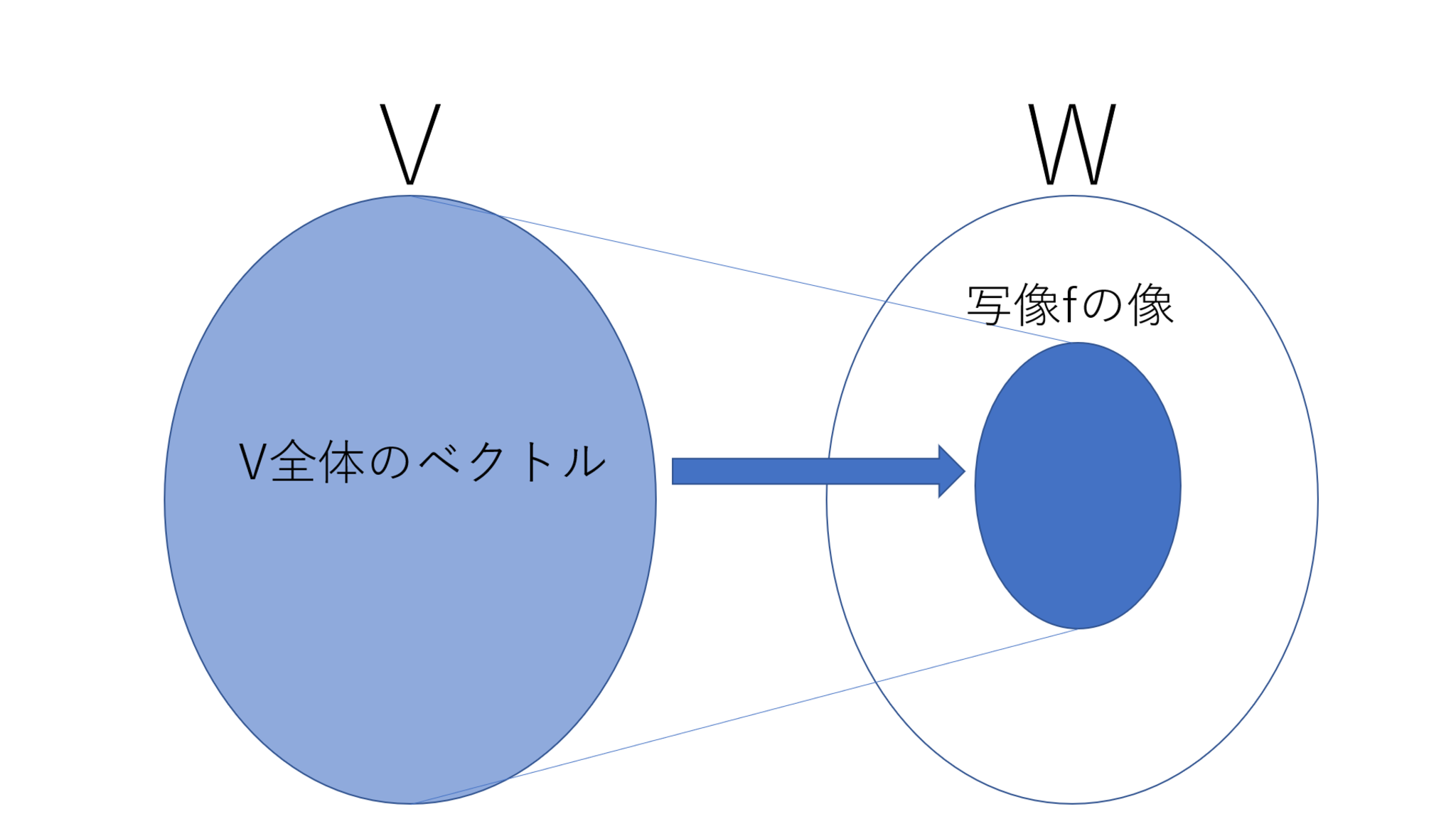 像
像
見てもらえば分かる通り,核や像は全く難しい概念ではございません.安心して下さい!
下に定義を載せておきます.
$f:V\rightarrow W$に対し
核とは次のようなベクトルの集合である.
$Ker\hspace{1pt}f=\lbrace x\in V \vert f(x)=0
\rbrace$
また,像とは次のようなベクトルの集合である.
$Im\hspace{1pt}f=\lbrace f(v)\vert v\in V \rbrace$
核は出力が$0$である様な$V$の部分空間,像は入力に対応する$W$の部分空間です.
さて,核と像がほんわかと理解できたところで,次元定理を早速見てみましょう.
次元定理
ではまずその主張から見ていきましょう.
$V,W$を線形空間とする.線形写像$f:V\rightarrow W$について,
$dim\hspace{1pt}V=dim\hspace{1pt} (Kerf)+dim\hspace{1pt} (Imf)$
が成り立つ.
さて,この定理で私が一番感心したところが,核と像の次元の関係が,写された後の空間$W$によらないということなのです.
これ,すごくないですか??線形写像をどのようにとっても,写される前の空間だけ決まっていれば,写された後の空間がどんなに広くても狭くても,核と像の次元の和は一定なんです.
では,証明していきましょう.(ここから先は少し固い話になってしまうので,読み飛ばしてもらってかまいません)
次元定理の証明
$V$の次元を$n$とする.
$Kerf$の基底を$v_1,v_2,\ldots ,v_s$とし,$Imf$の基底$u_1,u_2,\ldots ,u_{n-s}$とする.このとき,$f(a_1)=u_1,\ldots ,f(a_{n-s})=u_{n-s}$を満たす$a_1,\ldots ,a_{n-s}$が存在する.以下、$t=n-s$とする.
$\lbrace v_1,v_2,\cdots,a_s,a_1,a_2,\cdots,a_t \rbrace $が$V$の基底となることを示す.
任意の$x\in V$をとる.このとき,$f(x)=c_1u_1+\cdots +c_tu_t$とすることができる.これを$f$が線形写像であることを用いてうまく変形すると,$f(x-(c_1a_1+\cdots +c_ta_t))=0$となる.つまり,$x-(c_1a_1+\cdots +c_ta_t)\in Kerf$で,$$x-(c_1a_1+\cdots +c_ta_t)=d_1v_1+\cdots +d_tv_t$$
よって,$x=c_1a_1+\cdots +c_ta_t+d_1v_1+\cdots +d_tv_t$と$\lbrace v_1,v_2,\cdots,a_s,a_1,a_2,\cdots,a_t \rbrace$の線形結合で$x$を表せた.
$\lbrace v_1,v_2,\cdots,v_s,a_1,a_2,\cdots,a_t \rbrace $が線形独立であることを示す.
$x_1v_1+\cdots+x_sv_s+y_1a_1+\cdots+y_ta_t=0$であると仮定すると,両辺を$f$で写せば,$y_1u_1+\cdots+y_tu_t=0$となるが,$\lbrace u_1,u_2,\cdots,u_t \rbrace $は$Imf$の基底で有るため,線形独立だから,$y_1=\cdots=y_t=0$.
元の式にこれを代入すると, $x_1v_1+\cdots+x_sv_s=0$で,同様に$x_1=\cdots=x_s=0$.よって $\lbrace v_1,v_2,\cdots,v_s,a_1,a_2,\cdots,a_t \rbrace $が線形独立であることがいえ,定理は示された.
どうでしょうか?なかなかいけてる証明だと思いませんか?
$Kerf$と$Imf$を定めるものが、そのままかぶりなく$V$を作っているんですって。
形式的には理解が可能ですが,定性的に理解しようとすると少し躓いてしまうかなと思います.(ですが,よく考えてみると自明っぽいかな?という気もしてきます.$Kerf$の定義が$f(a)=0$なる$a$の集合で,$0$は$Imf$の基底にはなりえませんから.)
ここまでの話で,次元定理のぱわーを感じ取ってもらえたでしょうか?最後に少しだけ余談をしてこの記事を締めたいと思います.
最後に
この記事でもっとも伝えたかったのは,抽象的な数学も面白い!!ということです.今回お話ししたのは次元定理というそこまで高度ではない物でしたが,後々選択公理だったり,次元定理の一般ver.の準同型定理なんてのもあったりして,だんだん訳が分からなくなってきます.それでも少し競技数学や受験数学に疲れたりしたときは,抽象数学の世界をさまよってみたりするのもよいと思います.
大分長くなってしまいましたが,皆さんがこれからも楽しく数学に触れていかれることを願っています!!
