空間の曲率とは？～曲線・曲面の曲率とその計算方法～

Preface

こんにちは, 首藤です. Wathematicaアドベントカレンダー企画最終日の記事になります. 初日の記事も僕が書いたのでオセロ理論から全部の記事を僕が書いたことになりますね.

さて, この記事のテーマは”曲率”です. その名の通り, 空間の曲がり具合を表す量なのですが, 具体的にはどのように定まっているのか, またどうすれば計算できるのか, などについて書いていこうと思います.
前提知識は1年次程度の数学？だと思います. 一応軽く証明を書いたりはしますが, 読み飛ばしちゃって全然OKです.

平面曲線の曲率

定義

まずは, 平面内の曲線について考えていきましょう. $c:[a,b]\rightarrow \mathbb{R}^2$をなめらかな曲線とします. このままではちょっと扱いにくいので, 弧長パラメータ変換(arc length parametrization)というのを施します. これは, 曲線の形はそのままに, 進み方をちょっといじってそのスピードが一定になるようにする変換のことです.
（ここは読み飛ばして大丈夫です）具体的には
$$s(t)=\int_a^t \|c'(u)\|du$$
として$s:[a,b]\to[0,l]$ ($l$は曲線$c$の長さ) を定め, その逆関数$t:[0,l]\to[a,b]$を取ります.
そして $\gamma(s)=c(t(s))$ と合成で定めたものが, 弧長パラメータ変換された曲線です. これからは主にこっちの曲線を扱っていきます.
こいつにはいくつか良い性質があって, そのひとつが「速度ベクトルとその微分が直交する」ということです. 一応証明をしておきましょう. $T(s)=\gamma'(s)$とすると, $T(s)$の大きさ$\|T(s)\|$は常に一定なので,
$$\langle\ T(s),T(s)\ \rangle=\|T(s)\|^2=Const$$
ここで, $\langle,\rangle$は内積です. これを微分して,
$$0=\langle\ T'(s),T(s)\ \rangle+\langle\ T(s),T'(s)\ \rangle=2\langle\ T(s),T'(s)\ \rangle$$
よって$T(s)$と$T'(s)$の内積が0, つまり直交していることがわかりました.
さて, ここで方向ベクトル$\mathbb{n}$を, $T$を正の方向に90°回転させたものと定めます. 当然, この$\mathbb{n}$も$T$と直交しているので, ある実数$\kappa$を用いて$T'=\kappa\mathbb{n}$と書くことができます. 図にするとこうです.
crv1
この$\kappa$のことを, $\gamma$の($\gamma(s)$での)曲率(curvature)といいます.

具体例

ではいくつか具体的な平面曲線の曲率を求めてみましょう.

円周の曲率

$c(t)=(r\cos t,r\sin t)$の曲率を求めてみましょう. 計算は省きますが, 弧長パラメータ変換すると, $\gamma(s)=(r\cos\dfrac{s}{r},r\sin\dfrac{s}{r})$となります. 次に必要なベクトルを計算すると,
$T(s)=\gamma'(s)=(-\sin\dfrac{s}{r},\cos\dfrac{s}{r})$
$T'(s)=-\dfrac{1}{r}(\cos\dfrac{s}{r},\sin\dfrac{s}{r})$
$\mathbb{n}(s)=(-\sin(\dfrac{s}{r}+\dfrac{\pi}{2}),\cos(\dfrac{s}{r}+\dfrac{\pi}{2}))=-(\cos\dfrac{s}{r},\sin\dfrac{s}{r})$
と出ました. よって$T'(s)=\dfrac{1}{r}\mathbb{n}(s)$と書けるので, 半径$r$の円周の曲率は$\dfrac{1}{r}$となります. 曲率半径は曲率の逆数で定まりますが, それにはこういう背景があったんですね.

直線の曲率

直線の曲率は0であってほしいですよね. 実際そうなります.
$c(t)=(t,0)$とすると, これは既に弧長パラメータになってます. なので,
$T(t)=c'(t)=(1,0)$
$T'(t)=(0,0)$
$\mathbb{n}(t)=(0,1)$
となって曲率は0です. $T'$が0なんで$\mathbb{n}$を計算するまでもなかったんですが一応.

曲面の曲率

曲線の曲率を定めることはできたけど, 次元が上がって曲面になったらどうするの？っていう疑問が浮かぶかもしれません. もちろん曲面にも曲率を定めることはできるし, 何なら超曲面（$n+1$次元ユークリッド空間に埋め込まれた$n$次元多様体のこと. 要するに次元が高い曲面）にも似たような感じで曲率が定まります. ですがその定め方はいくらか面倒になります. 本記事の目標はその構成を理解し, また具体的に計算できるようになることです. 厳密性とか証明とかはだいぶ飛ばすけどね.

定義

$M$を曲面とし, その各点$p$に単位法ベクトル$N_p$があるとします（単位は大きさが1の意）. また, $p$での接平面を$T_pM$と書くことにします. つまり, $N_p\perp T_pM$が成り立っています. 図にするとこんな感じ.

crv2
うーん図がヘタクソ.
さて, $M$の$p$での曲率を定めていきたいんですが, いくつかステップを踏む必要があります.
まず, 単位接ベクトル$X_p$をとります. すると, $X_p$と$N_p$の張る平面によって曲面$M$が切断され, 曲線が出来上がります.

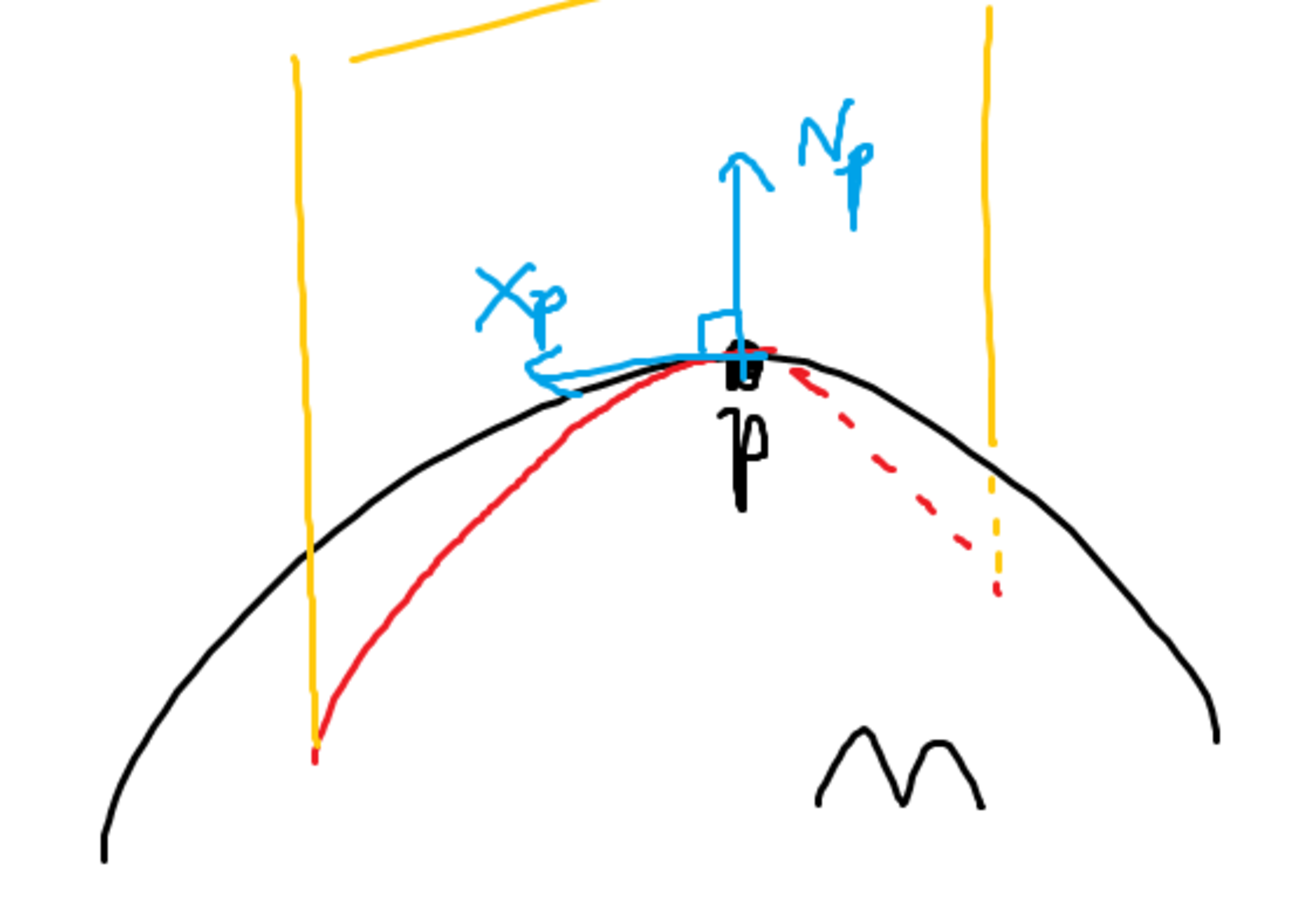crv3

伝わるかな…… オレンジが張られる平面, 赤がそれで切断されてできた曲線のつもりです……
すると, このオレンジの平面内に赤の曲線が描かれている状態になります. さっきやった平面曲線が作れたわけです. 同じ要領で曲率を求めたとしましょう.
（補足：パラメータは$p$での微分が$X_p$になるようにとっておき, $\mathbb{n}$は$N_p$として計算する）
これは最初に取った単位接ベクトル$X_p$ごとに決まるので, 関数として$\kappa(X_p)$と書くことにします. さて, これで曲率を得られましたが, 関数の形ではちょっと扱いにくいので, 代表的な値を取り出していきます.
この関数$\kappa$の最大値を$\kappa_{max}$, 最小値を$\kappa_{min}$とします. この2つの実数を主曲率(principal curvature)といいます. そして, これらの平均$\dfrac{\kappa_{max}+\kappa_{min}}{2}$を平均曲率(mean curvature), 積$\kappa_{max}\kappa_{min}$をガウス曲率(Gaussian curvature)といいます. 単に曲率とだけ言った場合は, ガウス曲率を指すことが多いです.

余談：ガウス驚異の定理

実はガウス曲率は, 等長同型な曲面間で保存されます. 等長同型っていうのは, 長さを変えないようにぐにゃぐにゃいじって移り合うもののことをいいます. 平面と円筒とかがそうですね. 紙をそのままぐるっと巻けば円筒になりますよね？そんな感じです.
”等長同型ならばガウス曲率は同じ”ということなので, 対偶をとって”ガウス曲率が違うなら等長同型でない”ことがいえます. これは数学でよくやる分類手法で, そのまま同型かどうか調べるのは大変なので, 特徴的な量を調べて判断しようって感じです.
この定理を”ガウス驚異の定理”っていいます. 本当です. あのガウスがびっくりするくらいの定理だったってことで, こういう名前になったらしいです. 原語では$\mathrm{Gauss's\ Theorema\ Egregium}$です. かっこいいですね.
この定理の有名な帰結として, ”地球の等長な地図は作れない”ことがあります. 曲面の等長な地図が書けるっていうのは, 地図（平面）と等長同型であるってことですが, 地球（球面）のガウス曲率は正の値, 平面のガウス曲率は0なので, どうあがいても等長同型にはなりえません. そんなわけで, 地球の等長な地図は書けないんです. メルカトル図法とかモルワイデ図法とか色々ありますが, そのどれも何かしらの量はおかしくなっています. よく見る地図は端っこがやたらでかくなってたりするでしょ？

具体例

これだけだと簡単な形の曲面に対してしか曲率を求められないんですが, とりあえずできるものを2つほどやってみましょう.

球面

球面は対称なので, すべての点での曲率が同じになります. 法ベクトルは外に向かうようにとっておきましょう. 単位接ベクトルはどう取ってもそれらによる球面の切断は円周になります.

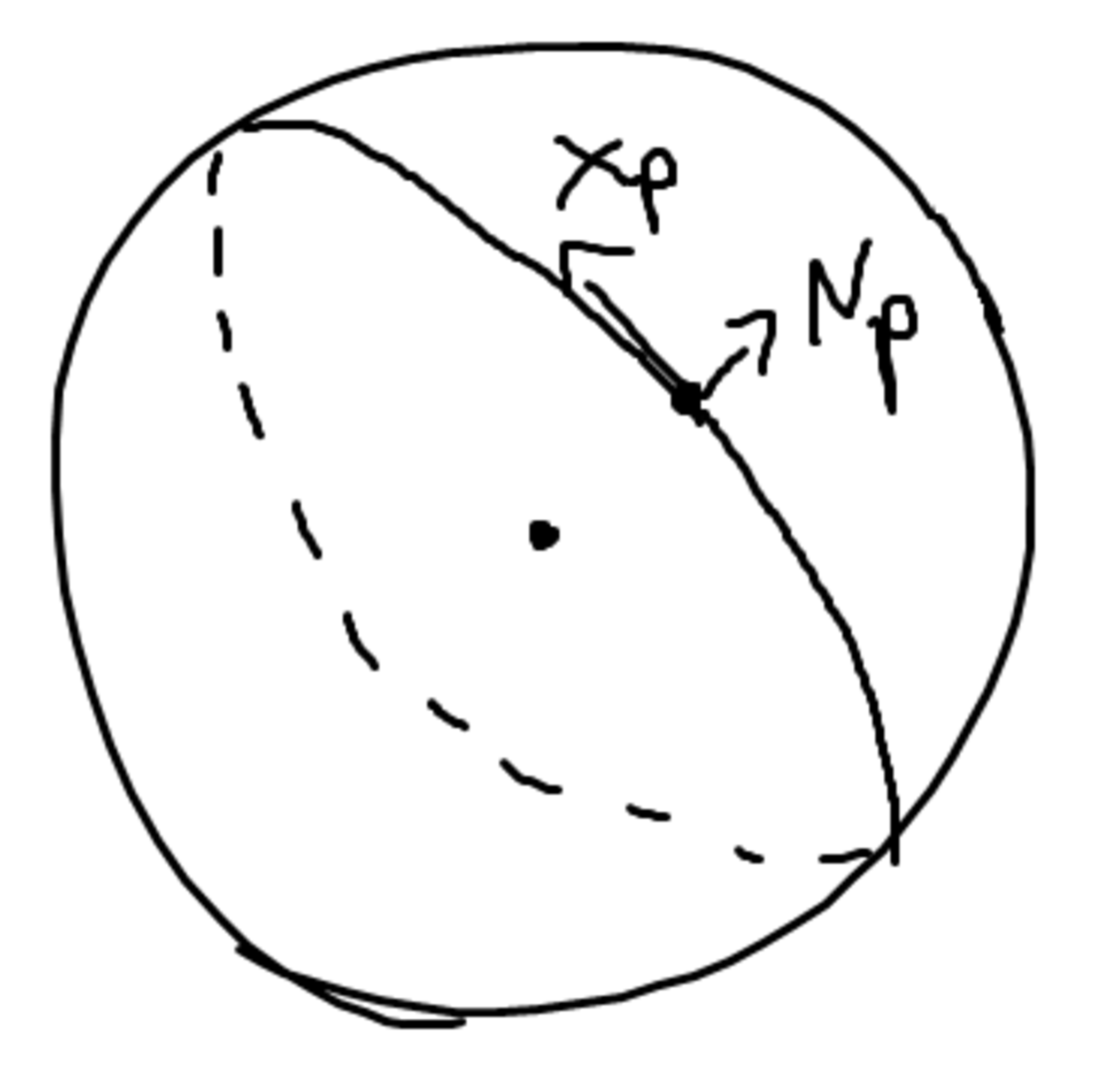crv4

こんな感じです. 頭の中で補正してください…
さて, さっきやったように, 半径$r$の円周の曲率は$1/r$でした. しかし, ここで注意しなければならないのが, 法ベクトル(上で言うところの$\mathbb{n}$)が逆になっている点です. この場合曲率は$-1$倍されます. よって主曲率はともに$-1/r$で, 平均曲率はそのまま$-1/r$, ガウス曲率は$1/r^2$となります. 絶対に0にはなりませんね.

平面

では平面の曲率を調べていきましょう. とは言ってもすごく簡単で, 切断っていうのは平面との共通部分なので直線になります. なので曲率は0となって, 平均曲率, ガウス曲率ともに0になります. これは球面のガウス曲率と異なるので, 球面と平面は等長同型ではないことになります.

ガウス曲率の計算方法

ガウス曲率を計算する方法は色々ありますが, ここではshape operatorを使った方法を採用することにします. そのために, まず方向微分というものを導入します.

方向微分

多様体論でのベクトル場とかの扱いを知っている方は脳内で適当に置き換えてください.
点$p$を始点とするベクトル$X_p=(a,b,c)$による, ベクトル場$Y=(f(x,y,z),g(x,y,z),h(x,y,z))$の方向微分を$D_{X_p}Y$と書くことにしましょう. これを, $X_p$を微分作用素$a\dfrac{\partial}{\partial x}|_p+b\dfrac{\partial}{\partial y}|_p+c\dfrac{\partial}{\partial z}|_p$とみて, $D_{X_p}Y:=(X_p(f),X_p(g),X_p(h))$と定めます. 成分でもうちょっと明示的に書くと, $D_{X_p}Y=\left(a\dfrac{\partial f}{\partial x}(p)+b\dfrac{\partial f}{\partial y}(p)+c\dfrac{\partial f}{\partial z}(p),\ a\dfrac{\partial g}{\partial x}(p)+b\dfrac{\partial g}{\partial y}(p)+c\dfrac{\partial g}{\partial z}(p),\ a\dfrac{\partial h}{\partial x}(p)+b\dfrac{\partial h}{\partial y}(p)+c\dfrac{\partial h}{\partial z}(p)\right)$
となります. 複雑な気がしますが, 実際やってることは似たような微分の繰り返しなので意外と簡単です.

Shape Operator

それではshape operatorを定義します. ここまで来てしまえば簡単です. $M$を単位法ベクトル場$N$を持つ曲面, $p$をその点とします. 接ベクトル$X_p\in T_pM$に対し, $L_p(X_p):=-D_{X_p}N$と定めます. これがshape operatorです. マイナスがついているのに注意してください.
証明は省きますが, これは接空間$T_pM$内の線形変換になります. $L_p:T_pM\to T_pM$と見れて, しかもこれは線形写像ってことです. なにこれ？って感じかもしれませんが, ここですごい定理を紹介します.

これ凄くないですか？線形代数の授業で意味もわからず計算方法だけ覚えがちな固有値はこんな所でも出てきます. こっちを調べればわざわざ切断を考えたりしなくていいわけです.

具体例

さて, ではさっきの球面の曲率と平面の曲率をshape operatorを使って計算してみましょう.

球面の曲率

$M$を半径$r$の球面, $p=(p_x,p_y,p_z)$を$M$上の点とします. 単位法ベクトル場$N$は$\dfrac{1}{r}(x,y,z)$です. $v_1=(-p_y,p_x,0),\ v_2=(0,-p_z,p_y)$を$T_pM$の基底とすると, $L_p(v_1)=-D_{v_1}N=-(p_z/r,p_x/r,0)=-\dfrac{1}{r}v_1,\ L_p(v_2)=-D_{v_2}N=-(0,-p_z/r,p_y/r)=-\dfrac{1}{r}v_2$
よって$(L_p(v_1),L_p(v_2))=(v_1,v_2)\begin{pmatrix}-1/r&0\\0&-1/r\end{pmatrix}$となって, したがってこの基底に関する$L_p$の表現行列は$\begin{pmatrix}-1/r&0\\0&-1/r\end{pmatrix}$です. 以上から, 主曲率は$-1/r$, ガウス曲率は$1/r^2$であることが確認できました.

平面の曲率

$M=\mathbb{R}^2$を$xy$平面とすると, 法ベクトル場は$N=(0,0,1)$です. これは定数なので, 微分で定義されているshape operatorは0になります. よって固有値, 行列式ともに0です.

円筒の曲率

ついでに円筒の曲率も調べてみましょう. $M=\{(x,y,z)\in\mathbb{R}^2|x^2+y^2=r^2\}$を半径$r$の円筒とします.法ベクトル場は$N=(x/r,y/r,0)$です. 円筒は対称的なので$p=(r,0,0)$での曲率だけ調べればOKです. $T_pM$の基底を$e_1=(0,1,0),\ e_2=(0,0,1)$とします. これらにshape operatorを作用させると,
$L_p(e_1)=-D_{e_1}N=-(0,1/r,1)=-\dfrac{1}{r}e_1,\ L_p(e_2)=-D_{e_2}N=(0,0,0)$となります. よって表現行列は$\begin{pmatrix}-1/r&0\\0&0\end{pmatrix}$なので, 主曲率は0と$-1/r$, ガウス曲率は0となります. ガウス曲率は平面と一緒ですね.

おわりに

この記事ではshape operatorを使った曲率の計算方法を紹介しましたが, これでは曲率を計算できない曲面もあります. そもそも法ベクトル場がわかんなかったら計算のしようがありません. これをなんとかする方法の1つとして, 微分形式があります. 曲率形式っていう2形式とかそれに関する公式とかを使ってなんかがちゃがちゃやると曲率が計算できるんですが, これをちゃんとやるには, 微分形式だけでなくリーマン接続についてもある程度やる必要があります. なので本記事では触れませんでした. 気になる方はぜひ, 参考文献の"Differential Geometry"を読んでみてください. 多様体がまだよくわかってない方はその前に同著者の"An Introduction to Manifolds"（トゥー多様体）を読んで下さい. 僕のバイブルです.
曲率とは一体なんなのか, どうやったら計算できるのかが少しでもわかって頂けたなら幸いです.