2022/12/31に出題した自作問題とその解答

　あけましておめでとう。2023年の時空から挨拶を、 匿(Tock) である。何がおめでたいのかは各々の解釈に委ね、早速数学の話題に移りたい。良いだろうか。いや良くないか。良くないとは薄々察している。なので強引に行かせてもらう。善悪など高貴なる数学の前には些事に過ぎない。多分。

　新年最初の記事ということで、昨年最後に出題した 自作問題 を紹介しよう。

問題

匿(Tock)

　( @con_malinconia )
　
2022年最後の出題です。
三重以上の根号も「二重根号を含む」ものと考えます。
　
#二重根号
https://twitter.com/con_malinconia/status/1609145076785229824/photo/1

解答

　条件より${0}^{\circ}<\theta<{90}^{\circ}$の範囲で考えてよい。また、$$0<\sin\theta\leq 1\,\Longleftrightarrow\, 0< n\leq \left(\frac{5+3\sqrt{3}+2\sqrt{5}}{2}\right)^{4}<2894$$から、$n$としてありうる値の範囲は$1\leq n\leq 2893$である。

$$\begin{align*} \cos\theta &=\sqrt{1-\sin^{2}\theta} \\ &=\sqrt{1-\left(\dfrac{2\sqrt[4]{n}}{5+3\sqrt{3}+2\sqrt{5}}\right)^{2}} \\ &=\dfrac{\sqrt{\left(5+3\sqrt{3}+2\sqrt{5}\right)^{2}-4\sqrt{n}}}{5+3\sqrt{3}+2\sqrt{5}} \end{align*}$$であるから、
$${\color{red} \sqrt{\left(5+3\sqrt{3}+2\sqrt{5}\right)^{2}-4\sqrt{n}}} \qquad\dots({\rm i})$$の二重根号が外れるような$n$を探したい。
　$({\rm i})$を変形していくと、
$$\begin{align*} &\sqrt{\left(5+3\sqrt{3}+2\sqrt{5}\right)^{2}-4\sqrt{n}} \\ &\qquad =\sqrt{72+30\sqrt{3}+20\sqrt{5}+12\sqrt{15}-4\sqrt{n}} \\ &\qquad =\sqrt{2\left(36+6\sqrt{15}-2\sqrt{n}\right)+2\left(15\sqrt{3}+10\sqrt{5}\right)} \\ &\qquad =\sqrt{2\left(36+6\sqrt{15}-2\sqrt{n}\right)+2\sqrt{1175+300\sqrt{15}}} \end{align*}$$になる。ゆえに、$x_1=36+6\sqrt{15}-2\sqrt{n},$ $y_1=1175+300\sqrt{15}$とおけば、
$$\begin{align*} &\sqrt{\left(5+3\sqrt{3}+2\sqrt{5}\right)^{2}-4\sqrt{n}} \\ &\qquad =\sqrt{2x_1+2\sqrt{y_1}} \\ &\qquad ={\color{red} \sqrt{x_1+\sqrt{\left(x_1\right)^2-y_1}}+\sqrt{x_1-\sqrt{\left(x_1\right)^2-y_1}}} \end{align*}$$が従う。$({\rm i})$の二重根号を外したいので、
$$\begin{align*} \left(x_1\right)^2-y_1 &=\left(36+6\sqrt{15}-2\sqrt{n}\right)^2-\left(1175+300\sqrt{15}\right) \\ &=\left(4n+661\right)+132\sqrt{15}-144\sqrt{n}-24\sqrt{15n} \qquad\dots({\rm ii}) \end{align*}$$が何らかの式の平方になっている場合、綺麗に外せそうである。

　以上の考察を受け、$a, b, c, d$を整数として
$$(a+b\sqrt{15}+c\sqrt{n}+d\sqrt{15n})^2$$という式を立て、これが$({\rm ii})$に等しくなるような$(a,b,c,d,n)$の組を探す。
$$\begin{align*} &(a+b\sqrt{15}+c\sqrt{n}+d\sqrt{15n})^2 \\ &\qquad =\left(a^2+15b^2+c^2 n+15d^2 n\right)+2\left(ab+cdn\right)\sqrt{15} \\ &\qquad\qquad\qquad\qquad +2\left(ac+15bd\right)\sqrt{n}+2\left(ad+bc\right)\sqrt{15n} \end{align*}$$より、連立方程式
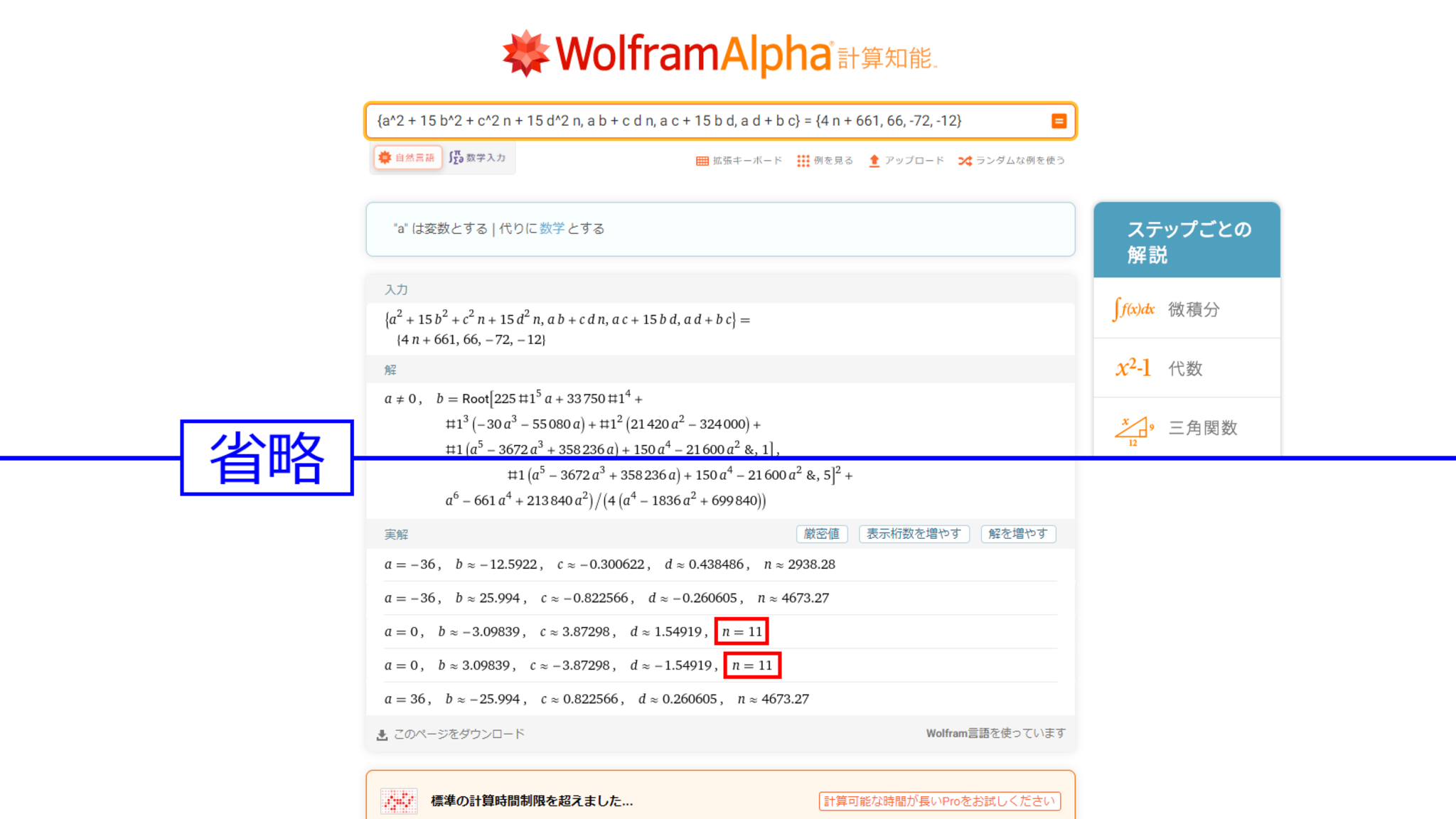
$$\begin{align*} \left\{\begin{array}{l} a^2+15b^2+c^2 n+15d^2 n &=& 4n+661 \\ ab+cdn &=& 66 \\ ac+15bd &=& -72 \\ ad+bc &=& -12 \end{array}\right. \end{align*}$$が整数解（$n>0$）をもつ場合を見つけよう。
　……とはいえ、手計算で見つけるのは大変そうなので（実際に大変である）、 WolframAlpha 先生の力を借りることにする。

この入力形式をつい最近知りました

　先生曰く、$n=11$のときに何かが起こっているようだ。これを確かめるべく、先程の連立方程式に$n=11$を代入し、再度先生にクエリを投げてみる。

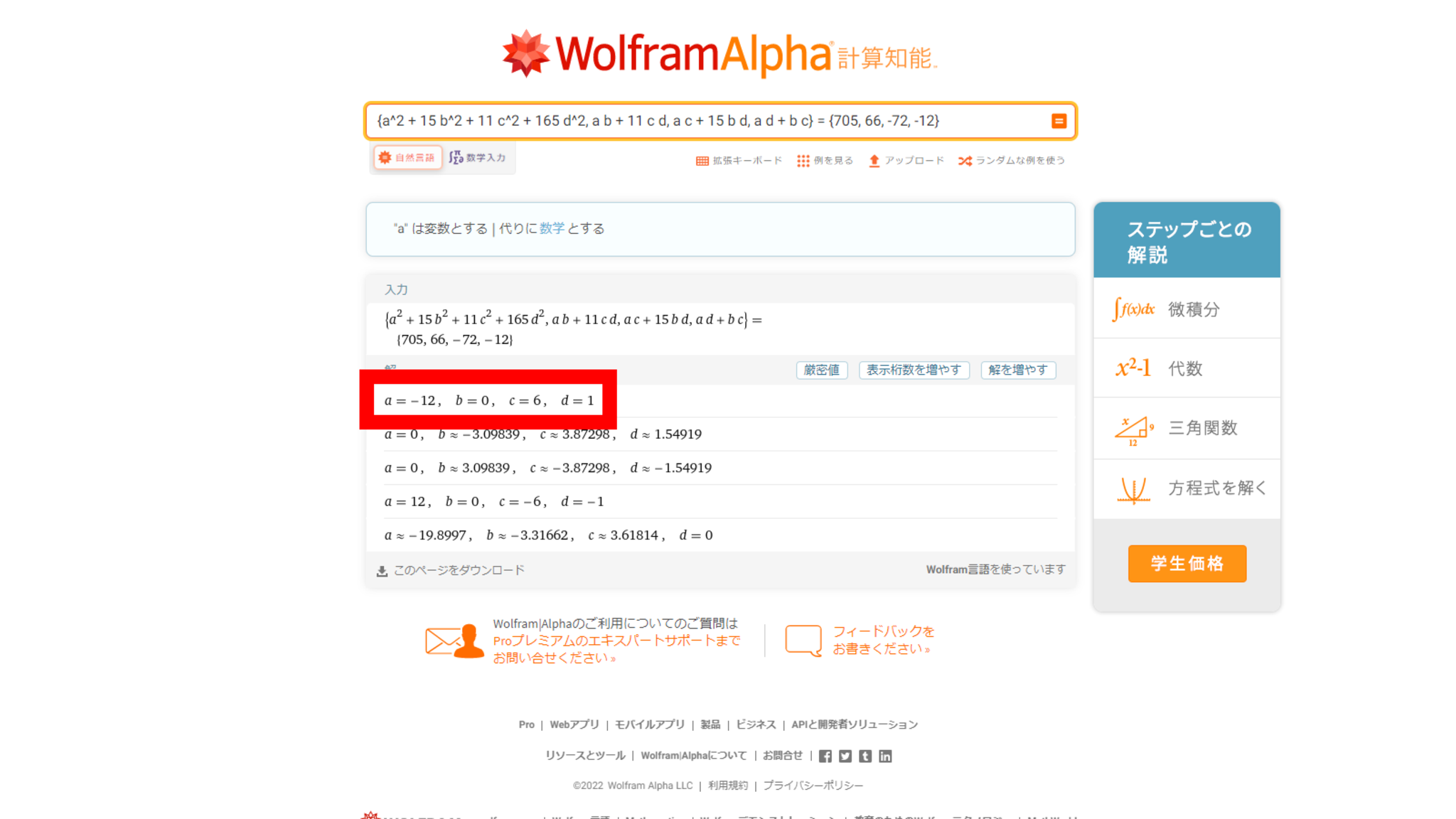あまりにも有能な先生様

　整数解が得られてしまった。$(a,b,c,d,n)=(-12,0,6,1,11)$のとき、上の連立方程式は満足される。すなわちこのとき、$({\rm ii})$は
$$\begin{align*} \left(x_1\right)^2-y_1 &=705-144\sqrt{11}+132\sqrt{15}-24\sqrt{165} \\ &={\color{red} \left(-12+6\sqrt{11}+\sqrt{165}\right)^2} \end{align*}$$と変形され、$x_1=36-2\sqrt{11}+6\sqrt{15}$とあわせて
$$\begin{align*} &\sqrt{\left(5+3\sqrt{3}+2\sqrt{5}\right)^{2}-4\sqrt{n}} \\ &\qquad =\sqrt{x_1+\sqrt{\left(x_1\right)^2-y_1}}+\sqrt{x_1-\sqrt{\left(x_1\right)^2-y_1}} \\ &\qquad =\sqrt{x_1+\left(-12+6\sqrt{11}+\sqrt{165}\right)}+\sqrt{x_1-\left(-12+6\sqrt{11}+\sqrt{165}\right)} \\ &\qquad ={\color{red} \sqrt{24+4\sqrt{11}+6\sqrt{15}+\sqrt{165}}+\sqrt{48-8\sqrt{11}+6\sqrt{15}-\sqrt{165}}} \qquad\dots({\rm iii}) \end{align*}$$を得る。

　$({\rm iii})$まで来ればあと一息である。
$$\begin{align*} \sqrt{24+4\sqrt{11}+6\sqrt{15}+\sqrt{165}} &=\sqrt{\left(6+\sqrt{11}\right)\left(4+\sqrt{15}\right)} \\ &=\dfrac{1}{2}\sqrt{12+2\sqrt{11}}\sqrt{8+2\sqrt{15}} \\ &={\color{red} \dfrac{1}{2}\left(1+\sqrt{11}\right)\left(\sqrt{3}+\sqrt{5}\right)} \\ \end{align*}$$および
$$\begin{align*} \sqrt{48-8\sqrt{11}+6\sqrt{15}-\sqrt{165}} &=\sqrt{\left(6-\sqrt{11}\right)\left(8+\sqrt{15}\right)} \\ &=\dfrac{1}{2}\sqrt{12-2\sqrt{11}}\sqrt{16+2\sqrt{15}} \\ &={\color{red} -\dfrac{1}{2}\left(1-\sqrt{11}\right)\left(1+\sqrt{15}\right)} \\ \end{align*}$$が簡単に分かるので、$({\rm iii})$に代入すれば
$$\begin{align*} &\sqrt{\left(5+3\sqrt{3}+2\sqrt{5}\right)^{2}-4\sqrt{n}} \\ &\qquad =\sqrt{24+4\sqrt{11}+6\sqrt{15}+\sqrt{165}}+\sqrt{48-8\sqrt{11}+6\sqrt{15}-\sqrt{165}} \\ &\qquad ={\color{red} \dfrac{1}{2}\left(\left(1+\sqrt{11}\right)\left(\sqrt{3}+\sqrt{5}\right)-\left(1-\sqrt{11}\right)\left(1+\sqrt{15}\right)\right)} \qquad\dots({\rm iv}) \end{align*}$$となって、$({\rm i})$の二重根号が完全に外れた。

　$n=11$は最初に求めた$n$の範囲に含まれているため、本問の答えとして$\bbox[#66ffcc]{11}$が挙げられる。

あとがき

　ただただWolframalpha先生の凄さを噛みしめる1問であった。
　なお、解答で求めたように$n=11$かつ${0}^{\circ}<\theta<{90}^{\circ}$としたとき、$\cos\theta$の値は
$$\cos\theta=\dfrac{\left(1+\sqrt{11}\right)\left(\sqrt{3}+\sqrt{5}\right)-\left(1-\sqrt{11}\right)\left(1+\sqrt{15}\right)}{2\left(5+3\sqrt{3}+2\sqrt{5}\right)}$$となる($\because ({\rm iv})$)。これを整理すると
$$\cos\theta=1-\dfrac{\left(1+\sqrt{3}\right)\left(1+\sqrt{5}\right)-2\left(1+\sqrt{11}\right)}{-7+4\sqrt{3}+3\sqrt{5}}$$のようにも書けて、個人的にはこちらのほうが綺麗に見えるのだがいかがだろうか。

1箇所だけ四乗根が現れている

　それから$n=11$以外の自然数解を発見された方は是非ご一報を。無いとは思うけれども。