調和性から見た射影幾何学（日本語版）

調和性から見た射影幾何学

（本記事はこちらの記事　 https://mathlog.info/articles/3835 　の日本語版です。若干の加筆修正と補足を加えています。）

非調和比の幾何学的導入

非調和比の概念は射影幾何学の色々な本で現れる。例えば、Cremonaの射影幾何学原論やBertiniの本などでみられる。非調和比を取り扱った本も存在する。なぜ非調和比がそれほど重要なのかは、それが4点からなるrangeの射影に関する完全不変量だからである。特に調和性は射影平面上で幾何学的に特別な意味を持つ。
非調和比、特に調和性からみた射影幾何学をみていこう。

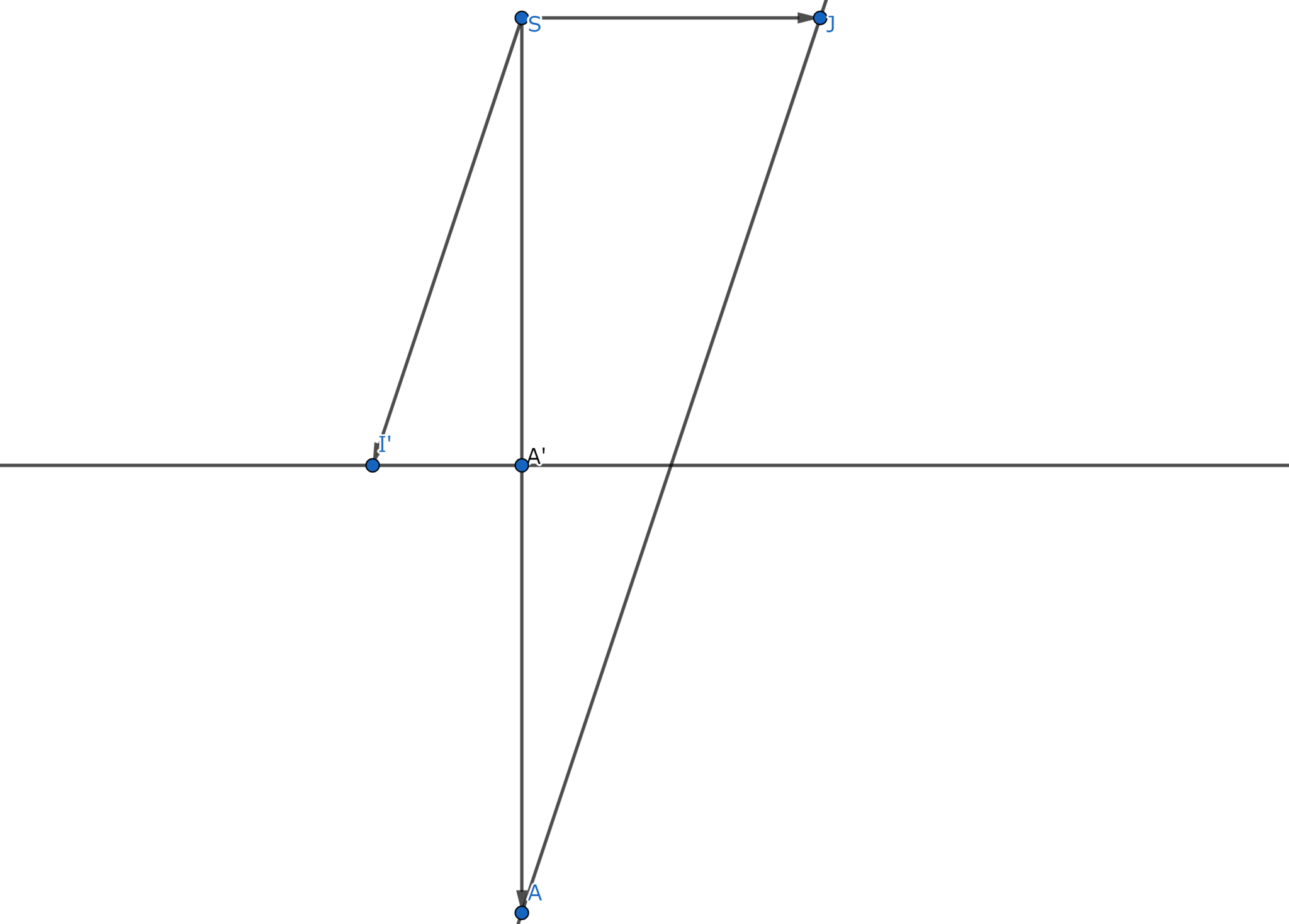相似な三角形
平面上の上図において相似な三角形$ SAJ,A'SI'$より$ JA/JS = I'S/I'A' $ よって $ JA.I'A' = JS.I'S $　が成り立つ。同様にperspectiveな他の点 $ B,B'$ を考えると$ JB.I'B' = JS.I'S$が成り立つ。よって、
$$ JA.I'A' = JB.I'B' $$
が成り立つ。つまりこの値はperspectiveな点の取り方に依らない。この値を$k$と表すとする。すると
$$ AB = JB - JA = k/I'B' - k/I'A' = k.(I'A'-I'B')/I'A'.I'B' = k.B'A'/I'A'.I'B'$$
が成り立つ。他のperspectiveな点 $ C,D$についても同様に成り立ち、これらの比を計算すると
$$ AC/BC:AD/BD = A'B'/B'C':A'D'/B'D'.$$
このperspectivityに関する定数比を非調和比という。

非調和比の定義

初等的な定義

直線上の４つの異なる点$ A,B,C,D $に対して
$$ (ABCD) = AC/BC : AD/BD $$
と定義する。ただし$ XY $は2点$ X,Y $の距離を表すとする（無限の距離を含む）。ここで$XY$は符号を含むものとする。つまり点$X,Y$は有限の距離にある場合は向きの付いた適当なアフィン直線上で考えるものとする。（射影直線は向き付けできない。）向きを変更しても$ AC/BC$ と $ AD/BD$はそれらの値が変わらないため向きの取り方に依らない。

斉次座標を用いた定義

直線上の４つの斉次座標$ \lambda_1,\lambda_2,\lambda_3,\lambda_4$に対して
$$ (\lambda_1\lambda_2\lambda_3\lambda_4)= |\lambda_1\lambda_3|/|\lambda_2\lambda_3|:|\lambda_1\lambda_4|/|\lambda_2\lambda_4|$$
と定義する。ただし、$|\lambda \mu|$は斉次座標$\lambda, \mu$をベクトルと見た時の行列式とする。

基本的な性質

perspectivity に関する不変性

導入でみたように、非調和比はperspectiveなrangeの取り方に依らない。斉次座標による非調和比の不変性は以下のようにして示される：
perspectivityはメビウス変換であるため非特異な行列$M$で変換すると
$$ |M\lambda_1M\lambda_i|/|M\lambda_2M\lambda_i| = |M(\lambda_1\lambda_i)|/|M(\lambda_2\lambda_i)| = |M||\lambda_1\lambda_i|/|M||\lambda_2\lambda_i| = |\lambda_1\lambda_i|/|\lambda_2\lambda_i| (i=3,4).$$

projectivity に関する完全不変性

完全性は以下の二つの性質によって導かれる：
・3点よりなるrangeを二つ用意すると、それらは射影的である
・固定された非調和比におけるrangeの第4点の一意性
同じ非調和比をもつ二つのrange$A,B,C,D; A',B',C',D'$を与える。それぞれ3点よりなる二つのrangeは射影的であるので、それらはperspectiveであると仮定してよい。すると$A'B'C'$と同じ直線上に$D$とperspectiveな点$D''$を見つけることができる。perspectivityより$(ABCD) = (A'B'C'D'')$を得る。しかし、仮定より$(ABCD)=(A'B'C'D')$であるので$(A'B'C'D') = (A'B'C'D'')$を得る。よって第4点の一意性より$D'=D''$が成り立つ。したがって、$A,B,C,D$と$A'B'C'D'$はperspectiveである。perspectivityの操作を何回も行うことにより主張を得る：$A,B,C,D$と$A'B'C'D'$が同じ非調和比を持つならば、それらは射影的である。

その他の性質

以下の性質を記載しておく（証明は省略する）：
$$(ABDC) = 1/(ABCD)$$
$$(ACBD) = 1-(ABCD)$$
$$(ACDB) = -1/(ABCD)$$
ただし、これらの値は適当なアフィン直線で考えるものとする。

調和性

定義

幾何学的定義

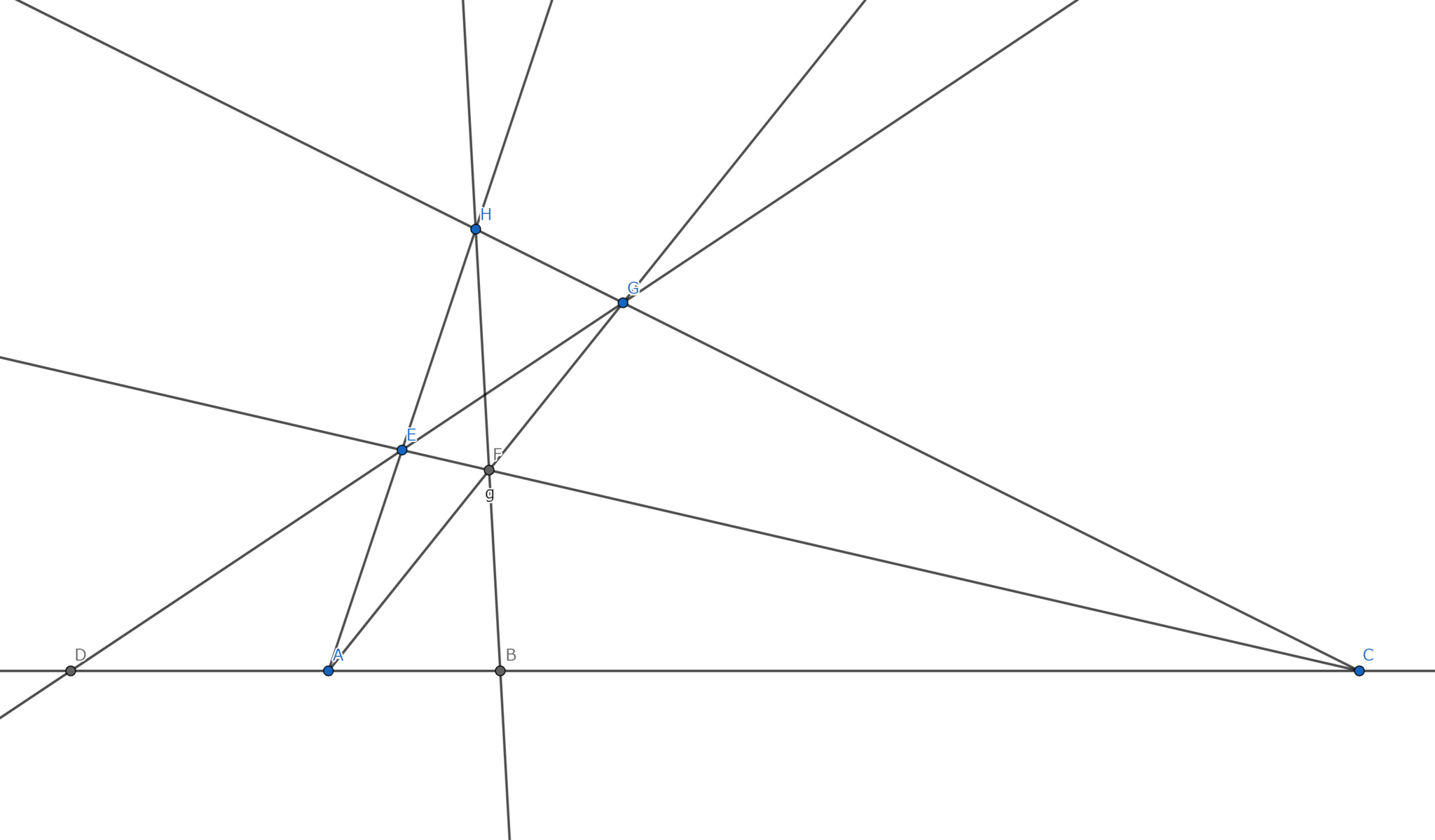Harmonic range
平面上のある直線上に異なる4点$A,B,C,D$を与える。点$A$から二つの直線を描き点$C$から二つの直線を描くと対角線$EG,FH$をもつ四角形$EFGH$を得る。さらに対角線に沿ってそれぞれ直線を引くと直線$AC$上に交点$B,D$をえ、これらの点$A,B,C,D$を調和的と言う。ここで点$A,C$からそれぞれ引く二つの直線はその取り方に依らないとする。

非調和比による定義

直線上に4つの異なる座標$\lambda_1,\lambda_2,\lambda_3,\lambda_4$を与え
$$ (\lambda_1\lambda_2\lambda_3\lambda_4)= |\lambda_1\lambda_3|/|\lambda_2\lambda_3|:|\lambda_1\lambda_4|/|\lambda_2\lambda_4| = -1:1$$
であるとき、これらの点は調和的である呼ぶ。

性質

定義の同値性

3点よりなる任意のrangeは$(-1:1),(1:1),(0:1)$に射影的であるので、range $(-1:1),(1:1),(0:1),D$に対して同値性を示せば十分である。

それらの４点が幾何学的定義において調和的であると仮定する。点$(0:1)$を通るように垂直線を引き、それぞれの点$(-1:1),(1:1)$から垂直線上で交わるように同じ側に二直線を引く。その時、点$D$を通る直線は水平線でなければならないので、$D$は無限遠点$(1:0)$となる。この状態で非調和比を計算すると、
$$((-1:1)(1:1)(0:1)(1:0)) = |\begin{bmatrix} -1 & 0 \\ 1 & 1 \\ \end{bmatrix}| / |\begin{bmatrix} 1 & 0 \\ 1 & 1 \\ \end{bmatrix}| : |\begin{bmatrix} -1 & 1 \\ 1 & 0 \\ \end{bmatrix}| / |\begin{bmatrix} 1 & 1 \\ 1 & 0 \\ \end{bmatrix}| = -1/1:-1/-1 = -1:1. $$
となる。従って、幾何学的定義において調和的な4点は非調和比の意味でも調和的である。

逆に、非調和比の意味で調和的と仮定する、つまり
$((-1:1)(1:1)(0:1)(\lambda_4:\lambda_4')) = -1/1 : -(\lambda_4'+\lambda_4)/(\lambda_4'-\lambda_4) = -1:1$。
この時、この式は線型方程式となるので第4の座標は一意的に定まり
$(\lambda_4:\lambda_4') = (1:0)$
となる。幾何学的な意味での調和性を示すには$(0:1)$を通る直線は垂直線である場合を証明すれば十分である。なぜならば、もし垂直でないならば$(0:1)$を固定する射影によって垂直になるようにすればよいからである。この時、4点は別の直線上の$(-t:1),(0:1),(t:1),(1:0) (t\not=0)$へと射影され、非調和比は$-1:1$のまま維持される。また$(1:0)$を通る直線は水平線である。従って、非調和比の意味での調和性は幾何学的定義においても調和的である。

方程式

$M,O,A_1,A_2$を直線上の4つの異なる点とし、それらは調和的とする。調和性より$MA_1/OA_1+MA_2/OA_2 = 0$を得る。$MA_i = MO+OA_i$であることを適用し、その結果を$MO$で割ると
$$(1/OM-1/OA_1)+(1/OM-1/OA_2) = 0$$
を得る。

一般化された調和性

任意の個数の点の「調和性」を定義するには、方程式における和の数を増やせばよい：
2点$M,O$を固定し、その直線上の$n$個の異なる点$A_i (i=1,...,n)$をとる。点$A_1,...,A_n$に対して調和性を以下の方程式で定義する：
$$\sum_{i=1,...,n} (1/OM - 1/OA_i) = 0.$$
更にもっと次の様に一般化することができる：
$$\sum_{\#I=r,I\subseteq\{1,...,n\}}\prod_{i\in I} (1/OM - 1/OA_i) = 0.$$

コメント

初等的な非調和比の定義はCremonaの射影幾何学原論で述べられている。非調和比の不変性は射影幾何学の色々な本で説明されているが完全不変性の証明は、調べた限りでは、射影幾何学原論でのみ示されており他の文献には無かった。
一般化された調和性の方程式はBoncelet, Jonquieres, Cremonaの文献で述べられており、最初の方程式はPonceletによって初めて導入され最後の方程式はJonquieresによって最初に導入された。
※誰が最初に導入したか十分に調べていないので目下調査中であるが、文献を調べてみると今の所彼らが最初に導入していた模様。

補足

各種定義

range : 同じ直線上の異なる点の集まり（非調和比を計算する際は順序も考慮される）。
perspectivity : 平面上のある点を中心として、ある直線から別の直線へと点を写す操作。元のrangeと写した先のrangeをperspectiveな関係にあるという。今でいう「射影」のこと。中心となる点は無限遠点でもよい。この時、中心の点を通る直線はすべて平行となる。
projectivity : perspectivity を有限回行う操作。この操作によって同様にprojectiveな関係が定義される。
（いずれの定義もcremonaの射影幾何学原論によるもの。）