積分公式
$\displaystyle \int_{-\infty}^{\infty}\frac{dx}{1+x^{2n}}= \frac{\pi}{n\sin{\frac{\pi}{2n}}}$の証明
関数$\displaystyle f(z)=\frac{1}{1+z^{2n}}$について
今回考える関数は、$\displaystyle f(z)=\frac{1}{1+z^{2n}}$ここで$n$は$n\in\mathbb{N}$とする。
$\displaystyle z^{2n}=-1$の解について
一般の形$x^{p}+q=0$の解は次のような形で与えられる。$x^p+q=0$の解は、 $$\begin{eqnarray} x=e^{\frac{1}{p}\{(2n-1)\pi i+\log q\}} (n=1,2,...,p)\end{eqnarray}$$
$x^p+q=0\Longleftrightarrow x^p =e^{\pi i+\log q}\Longleftrightarrow x =e^{\frac{1}{p}\{\pi i+\log q\}}$この時、$|x|=\bigl|e^{\frac{\pi i}{p}}\bigr|\cdot \bigl|e^{\frac{\log q}{p}}\bigr|=\bigl|e^{\frac{\log q}{p}}\bigr|$となる。ここで、代数学の基本定理よりから$p$次の代数方程式には、$p$個の解があるので偏角のみ変化させた場合も絶対値は変化しないことを利用して、次の様に解を仮定する。
$$x=e^{\frac{1}{p}\{(2n-1)\pi i+\log q\}} (n=1,2,3,...,p)$$この式が、解であるとは$x^p+q=0$を満たす$x$のはずなので
$$x^{p}=e^{p(\frac{1}{p}\{(2n-1)\pi i+\log q\}})=e^{(2n-1)\pi i+\log q}$$が成り立つ。ここで、$2n-1$は奇数であるから、$$x^{p}=-e^{\log q}=-q\Longleftrightarrow x^{p}+q=0$$が成立する。よって、今回求めるべき解は
$$x=e^{\frac{1}{p}\{(2n-1)\pi i+\log q\}} (n=1,2,...,p)$$
従って、今回求めるべきである$z^{2n}+1=0$は公式1から
$$z=e^{\frac{\pi ki}{n}-\frac{\pi i}{2n}}(k=1,2,...,2n)$$ である。
$\displaystyle \int_{C}\frac{dz}{1+z^{2n}}$の値
ここから、複素関数を用いて議論していく。まず、積分経路$C$を次の様に取る。
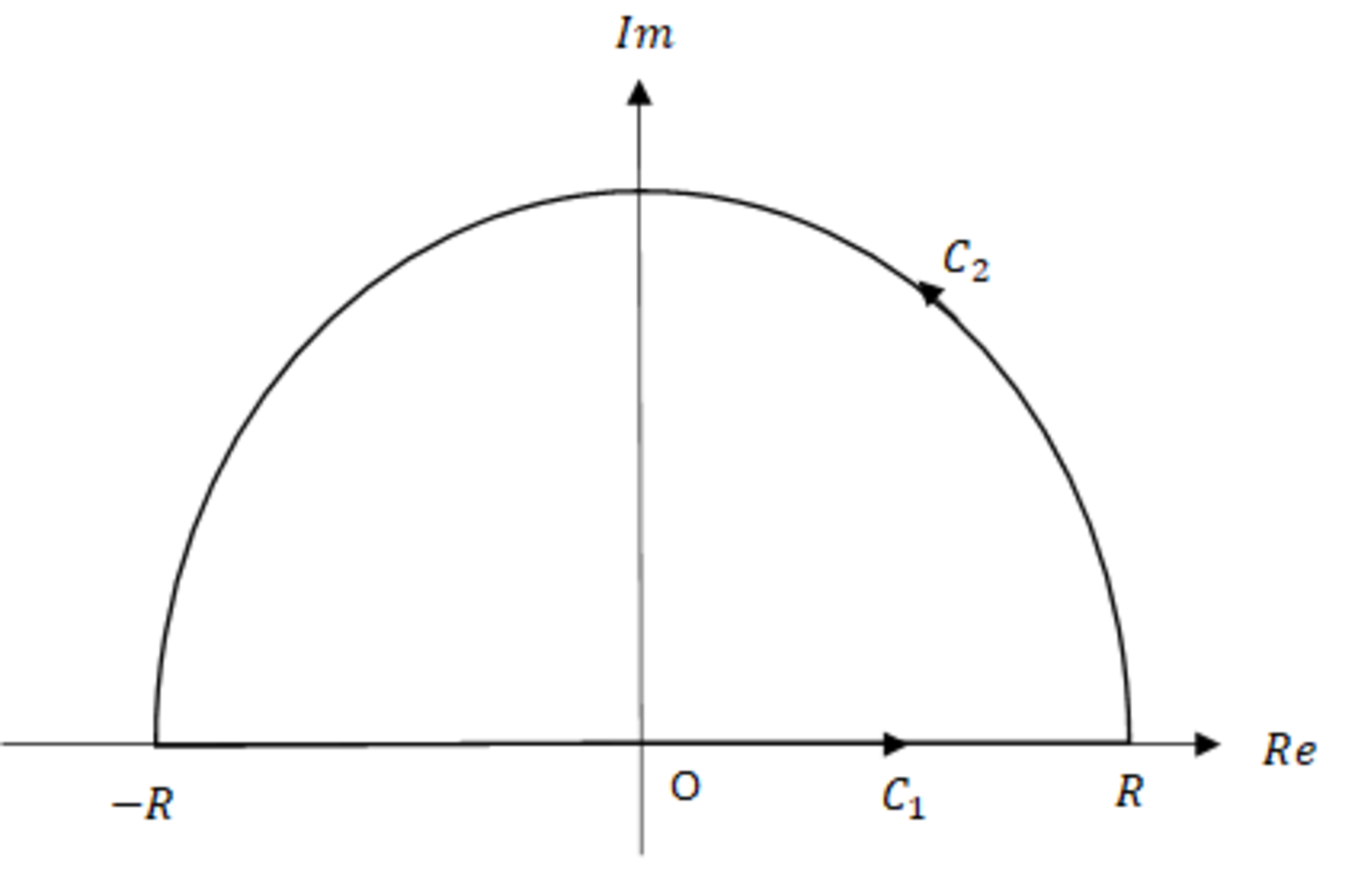 積分経路
積分経路
区分的に$C^{1}$級の有限個の単純閉曲線によって囲まれた(有界)平面領域$G$の境界$\partial G$は($G$に関して)正の向きに向きづけられているとする。この時平面領域$\bar{G}$上で正則な$C^{1}$級関数$f$に対して次が成り立つ。
$$\int_{\partial G}f(z)dz=0$$
複素線積分の定義 *1 とグリーンの定理 *2 を続けて用いると、$$\begin{eqnarray} \int_{\partial G}f(z)dz&=&\int_{\partial G}udx-vdy+i\int_{\partial G}vdx+udy\\ &=&-\int\int_{G}\biggl(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\biggr)dxdy+i\int\int_{G}\biggl(\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\biggr)dxdy\end{eqnarray}$$ここで、コーシー・リーマンの関係式 *3 より0になる。
ここで、$C_1$は実軸上にあり、$R$は十分大きいとする。$C_2$は半時計回りに$0\leq\theta\leq\pi$と取る。そうすると次のようになる。
$$\int_{C}f(z)dz=\int_{C_1}\frac{dz}{1+z^{2n}}+\int_{C_2}\frac{dz}{1+z^{2n}}$$積分経路$C_1$は実軸上にあるのでさらに書き換えると、$$\int_{C}f(z)dz=\int_{-R}^{R}\frac{dz}{1+z^{2n}}+\int_{C_2}\frac{dz}{1+z^{2n}}$$の様になる。
ここで、経路内の極は$n$個でありその値は、$\displaystyle e^{\frac{\pi ki}{n}-\frac{\pi i}{2n}}(k=1,2,...,n)$となっている。
従って、留数定理を用いて値を求める。
有限個の区分的に$C^{1}$級の単純平曲線によって囲まれた領域$G$の閉包$\overline{G} =G\cup\partial G$の上で、有限この内点$a_{1},a_{2},\cdots,a_{N}$を除いて正則な関数$f$について次が成り立つ。
$$\int_{\partial G}f(z)dz=2\pi i\sum_{n=1}^{N}Res_{a_{n}}f$$
参考文献[2]のp.305を参照されたい。
$z=z_0$で極を持つ関数$f(z)$が正則でかつ$\displaystyle f(z)=\frac{p(z)}{q(z)}$で表せるとき、留数は
$$Res[f(z),z_0]=\frac{p(z_0)}{q'(z_0)}$$で表せる。
$z=z_{0}$において$f(z)=\frac{p(z)}{q(z)}$が極を持つと仮定する。この時、$p(z_{0})=0$であることから$p(z)$を$z=z_{0}$付近でテイラー展開すると、$$\begin{eqnarray}
\nonumber q(z)&=&q(z_{0})+q'(z_{0})(z-z_{0})+\frac{1}{2}q''(z_{0})(z-z_{0})^{2}+...\\
&=&(z-z_{0})\{q'(z_{0})+\frac{1}{2}q''(z_{0})(z-z_{0})+...\}\end{eqnarray}$$となる。
次に関数$f(z)$が$z=z_{0}$で一位の極を持つとき
$$Res[f(z),z_{0}]=\lim_{z\rightarrow z_{0}}(z-z_{0})f(z)$$ が成り立つのでこれを用いて
$$\begin{eqnarray}
\nonumber Res[f(z),z_{0}]&=&Res\biggl[\frac{p(z)}{q(z)},z_{0}\biggr]\\ \nonumber
&=&\lim_{z\rightarrow z_{0}}(z-z_{0})\frac{p(z)}{q(z)}=\lim_{z\rightarrow z_{0}}\frac{p(z)}{q'(z_{0})+\frac{1}{2}q''(z_{0})(z-z_{0})+...}\\
&=&\frac{p(z_{0})}{q'(z_{0})}\end{eqnarray}$$
この公式1を用いて留数を求める。$p(z)=1$,$q(z)=1+z^{2n}$として考えると、留数は
$$Res\biggl[\frac{1}{1+z^{2n}},e^{\frac{\pi ik}{n}-\frac{\pi i}{2n}}\biggr]=\sum_{k=1}^{n}\frac{1}{2n}\frac{1}{e^{\frac{\pi ik}{n}-\frac{\pi i}{2n}}}$$となる。ここで、$\bigl|e^{\frac{\pi k}{n}-\frac{\pi}{2n}}\bigr|=1$より
$$\sum_{k=1}^{n}-\frac{1}{2n}\frac{1}{e^{\frac{\pi ik}{n}-\frac{\pi i}{2n}}}=\sum_{k=1}^{n}\frac{1}{2n} {e^{\frac{\pi ik}{n}-\frac{\pi i}{2n}}}=-\frac{1}{2n}e^{-\frac{\pi i}{2n}}\sum_{k=1}^{n}e^{\frac{\pi ik}{n}}$$と書ける。ここで、$\displaystyle \sum_{k=1}^{n}e^{\frac{\pi ik}{n}}$は、初項$e^{\frac{\pi ik}{n}}$公比$e^{\frac{\pi ik}{n}}$の等比数列の和なので、$$-\sum_{k=1}^{n}e^{\frac{\pi ik}{n}}=-\frac{e^{\frac{\pi i}{n}}(1-e^{\pi i})}{1-e^{\frac{\pi i}{n}}}=-\frac{2e^{\frac{\pi i}{n}}}{1-e^{\frac{\pi i}{n}}}$$これより求める値は、$$-\frac{1}{2n}e^{-\frac{\pi i}{2n}}\biggl(\frac{2e^{\frac{\pi i}{n}}}{1-e^{\frac{\pi i}{n}}}\biggr)=-\frac{1}{n}\biggl(\frac{e^{\frac{\pi i}{2n}}}{1-e^{\frac{\pi i}{n}}}\biggr)$$分母,分子に$e^{-\frac{\pi i}{2n}}$と、留数定理から$2\pi i$をかけて$\frac{e^{\frac{\pi i}{2n}}-e^{\frac{-\pi i}{2n}}}{2i}=\sin\bigl(\frac{\pi}{2n}\bigr)$の関係より
$$\frac{\pi}{n}\Biggl(\frac{1}{\frac{e^{\frac{\pi i}{2n}}-e^{\frac{-\pi i}{2n}}}{2i}}\Biggr)=\frac{\pi}{n\sin\bigl(\frac{\pi}{2n}\bigr)}$$以上より、$$\int_C\frac{dz}{1+z^{2n}}=\frac{\pi}{n\sin\bigl(\frac{\pi}{2n}\bigr)}$$ここから、各積分経路ごとに値を見ていく。
積分$\displaystyle \int_{0}^{\pi}\frac{iRe^{i\theta}}{1+R^{2n}e^{2ni\theta}}d\theta$の評価
まず全体で$R\rightarrow \infty$として考える。その時、経路$C_1$は、$$\int_{C_1}\frac{dz}{1+z^{2n}}=\lim_{R\rightarrow \infty}\int_{-R}^{R}\frac{dz}{1+z^{2n}}=\int_{-\infty}^{\infty}\frac{dz}{1+z^{2n}}$$の様になる。次に、経路$C_2$は、$z=Re^{i\theta}$と変数変換を行うと
$$\int_{C_2}\frac{dz}{1+z^{2n}}=\int_{0}^{\pi}\frac{iRe^{i\theta}}{1+R^{2n}e^{2ni\theta}}d\theta$$と書ける。従って、次の様に絶対値をとって評価する。
$$\biggl|\int_{0}^{\pi}\frac{iRe^{i\theta}}{1+R^{2n}e^{2ni\theta}}d\theta\biggr|<\int_{0}^{\pi}\biggl|\frac{iRe^{i\theta}}{R^{2n}e^{2ni\theta}}\biggr| d\theta=\lim_{R\rightarrow\infty}\frac{\pi}{R^{2n-1}}=0$$となるので、$$\int_{-\infty}^{\infty}\frac{dz}{1+z^{2n}}=\frac{\pi}{n\sin\bigl(\frac{\pi}{2n}\bigr)}$$に収束すること分かる。
$\displaystyle \int_{-\infty}^{\infty}\frac{1}{z^{2n}+a^{2n}}dz=\frac{\pi}{na^{2n-1}\sin{\frac{\pi}{2n}}}$の証明
次に考える関数は$\displaystyle f(z)=\frac{1}{z^{2n}+a^{2n}}$で$n\in \mathbb{N},|a|>0,a\in\mathbb{C}$とする。
$z^{2n}+a^{2n}=0$の解
公式1を用いると、$$z=e^{\frac{1}{2n}\{(2k-1)\pi i+2n\log a\}}=e^{\frac{\pi i}{2n}(2k-1)+\log a} (k=1,2,...,2n)$$これを用いて、$\displaystyle \int_{C}\frac{dz}{z^{2n}+a^{2n}}$を求める。
$\displaystyle \int_{C}\frac{dx}{z^{2n}+a^{2n}}$の値
積分経路$C$を図1の通りに取るとすると
$\displaystyle \int_{C}\frac{dx}{z^{2n}+a^{2n}}$に対し$x=e^{\frac{1}{2n}\{(2k-1)\pi i+2n\log a\}}=e^{\frac{\pi i}{2n}(2k-1)+\log a} (k=1,2,...,n)$が極である。
次に、$R$は十分大きいとして考える。
そうすると、$\displaystyle \int_{C}\frac{dz}{z^{2n}+a^{2n}}$は留数定理により求まる。この時留数は、$$\begin{eqnarray} Res\biggl[\frac{1}{z^{2n}+a^{2n}},e^{\frac{\pi i}{2n}(2k-1)+\log q}\biggr]&=\frac{1}{2n}\sum_{k=1}^{n}\frac{1}{e^{(\frac{\pi i}{2n}(2k-1)+\log q)(2n-1)}}\\ &=\frac{1}{2n}\sum_{k=1}^{n}\frac{1}{(-1)a^{2n}e^{-\frac{\pi i}{2n}(2k-1)-\log a}}\\ &=-\frac{1}{2na^{2n-1}}e^{-\frac{\pi i}{2n}}\sum_{k=1}^{n}e^{\frac{\pi i}{n}k}\\ &=\frac{1}{na^{2n-1}}\biggl(\frac{e^{\frac{\pi i}{2n}}}{e^{\frac{\pi i}{n}}-1}\biggr)\end{eqnarray}$$である。ここで留数定理より値が求まるので、$$2\pi i\biggl\{\frac{1}{na^{2n-1}}\biggl(\frac{e^{\frac{\pi i}{2n}}}{e^{\frac{\pi i}{n}}-1}\biggr)\biggr\}=\frac{\pi}{na^{2n-1}}\biggl(\frac{2i}{e^{\frac{\pi i}{2n}}-e^{-\frac{\pi i}{2n}}}\biggr)=\frac{\pi}{a^{2n-1}n\sin\bigl(\frac{\pi}{2n}\bigr)}$$の様になって結果
$$\int_{C}\frac{dz}{z^{2n}+a^{2n}}=\frac{\pi}{a^{2n-1}n\sin\bigl(\frac{\pi}{2n}\bigr)}...(1)$$
積分$\displaystyle \lim_{R\rightarrow\infty}\int_{0}^{\pi}\frac{iRe^{i\theta}}{R^{2n}e^{2ni\theta}+a^{2n}}d\theta$の評価
次に、積分経路は$C=C_1+C_2$であり、経路$C_1$に関しては実軸上を動いているから
$$\int_{C}\frac{dz}{z^{2n}+a^{2n}}=\int_{-R}^{R}\frac{dx}{x^{2n}+a^{2n}}+\int_{C_2}\frac{dz}{z^{2n}+a^{2n}}...(2)$$
の様に書ける。この時、$(R\rightarrow \infty)$として考えると、$$\lim_{R\rightarrow\infty}\int_{C}\frac{dz}{z^{2n}+a^{2n}}=\int_{-\infty}^{\infty}\frac{dx}{x^{2n}+a^{2n}}+\lim_{R\rightarrow\infty}\int_{C_2}\frac{dz}{z^{2n}+a^{2n}}$$経路$C_2$に関して$z=Re^{i\theta}$の様に変数変換すると微小量は、$dz=iRe^{i\theta}d\theta$となって、積分区間が$0\rightarrow\pi$であるので、$\displaystyle\lim_{R\rightarrow\infty}\int_{C_2}\frac{dz}{z^{2n}+a^{2n}}$は次の様に変化する。
$$\lim_{R\rightarrow\infty}\int_{C_2}\frac{dz}{z^{2n}+a^{2n}}=\lim_{R\rightarrow\infty}\int_{0}^{\pi}\frac{iRe^{i\theta}}{R^{2n}e^{2ni\theta}+a^{2n}}d\theta$$$\displaystyle \lim_{R\rightarrow\infty}\int_{0}^{\pi}\frac{iRe^{i\theta}}{R^{2n}e^{2ni\theta}+a^{2n}}d\theta$の絶対値をとって評価すると、$$\lim_{R\rightarrow\infty}\Biggl|\int_{0}^{\pi}\frac{iRe^{i\theta}}{R^{2n}e^{2ni\theta}+a^{2n}}d\theta\Biggr|<\lim_{R\rightarrow\infty}\Biggl|\int_{0}^{\pi}\frac{iRe^{i\theta}}{R^{2n}e^{2ni\theta}}d\theta\Biggr|\leq\lim_{R\rightarrow\infty}\int_{0}^{\pi}\frac{\bigl|iRe^{i\theta}\bigr|}{\bigl|R^{2n}e^{2ni\theta}\bigr|}d\theta=\lim_{R\rightarrow\infty}\frac{\pi}{R^{2n-1}}=0$$よって、$$\lim_{R\rightarrow\infty}\int_{C_2}\frac{dz}{z^{2n}+a^{2n}}=0$$従って、(1),(2)から
$$\int_{-\infty}^{\infty}\frac{dx}{x^{2n}+a^{2n}}=\frac{\pi}{a^{2n-1}n\sin \bigl(\frac{\pi}{2n}\bigr)}$$に収束する。
$\displaystyle \int_{-\infty}^{\infty}\frac{x^p}{x^{2n}+a^{2n}}dx=\frac{a^p\pi(1+\cos(p\pi))}{2na^{2n-1}\sin(\frac{p+1}{2n}\pi)}$の証明
$$z=e^{\frac{1}{2n}\{(2k-1)\pi i+2n\log a\}}=e^{\frac{\pi i}{2n}(2k-1)+\log a} (k=1,2,...,2n)$$
この結果を参考に今から議論をする。ここで$p$を次の2つの場合に分けて考えることができる。
$$\begin{eqnarray}
\int_{-\infty}^{\infty}\frac{x^{2n}}{x^{2n}+a^{2n}}dx (p=2n)\\
\int_{-\infty}^{\infty}\frac{x^{p}}{x^{2n}+a^{2n}}dx (p<2n)\end{eqnarray}$$ $p=2n$の時は下に示すように$+\infty$に発散していくことがわかる。
$$\int_{-\infty}^{\infty}\frac{x^{2n}}{x^{2n}+a^{2n}}dx=\int_{-\infty}^{\infty}1-\frac{a^{2n}}{x^{2n}+a^{2n}}dx=\int_{-\infty}^{\infty}dx-\int_{-\infty}^{\infty}\frac{a^{2n}}{x^{2n}+a^{2n}}dx=\infty$$
次に、$p<2n$の場合を取り扱うが、ここでも一点($p=2n-1$)で問題が発生するがその問題は後に任せるとして、$p<2n$の時の値を求めていく。
$\displaystyle\int_{C}\frac{z^p}{z^{2n}+a^{2n}}dz$の値
まず、$\displaystyle \int_{C}f(z)dz=\int_{C}\frac{z^p}{z^{2n}+a^{2n}}dz$に対し図1のような積分経路$C$を取る。
この時$R\rightarrow\infty$の極限を考える。 そうすると、$$\lim_{R\rightarrow\infty}\int_{C}\frac{z^p}{z^{2n}+a^{2n}}dz=\lim_{R\rightarrow\infty}\int_{-R}^{R}\frac{x^p}{x^{2n}+a^{2n}}dx+\lim_{R\rightarrow\infty}\int_{C_2}\frac{z^p}{z^{2n}+a^{2n}}dz$$の様に書ける。次に、留数定理より以下の様に書ける。
$$\int_{C}\frac{z^p}{z^{2n}+a^{2n}}dz=2\pi i\sum_{k}Res\biggl[\frac{z^p}{z^{2n}+a^{2n}},z_{k}\biggr]$$ここで、積分経路$C$内における$f(z)$の極は、$\displaystyle z=e^{\frac{\pi i}{2n}(2k-1)+\log a}$ $(k=1,2,...,n)$であるから、次のように書き換えられる。
$$\int_{C}\frac{z^p}{z^{2n}+a^{2n}}dz=2\pi i\biggl\{-\frac{a^{p}e^{-\frac{\pi i}{2n}(p+1)}}{2na^{2n-1}}\sum_{k=1}^{n}e^{\frac{pk}{n}\pi i+\frac{\pi i}{n}k}\biggr\}=2\pi i\biggl\{-\frac{a^{p}e^{-\frac{\pi i}{2n}(p+1)}}{2na^{2n-1}}\sum_{k=1}^{n}e^{\frac{k}{n}\pi(p+1)}\biggr\}$$シグマの中身を初項$e^{\frac{1}{n}\pi(p+1)}$公比$e^{\frac{1}{n}\pi(p+1)}$として計算すると、$$\begin{eqnarray}
2\pi i\biggl\{-\frac{a^{p}e^{-\frac{\pi i}{2n}(p+1)}}{2na^{2n-1}}\sum_{k=1}^{n}e^{\frac{k}{n}\pi(p+1)}\biggr\}&=&
2\pi i\biggl\{-\frac{a^{p}e^{-\frac{\pi i}{2n}(p+1)}}{2na^{2n-1}}\biggl(\frac{e^{\frac{\pi i}{n}(p+1)}(1-e^{\pi i(p+1)})}{1-e^{\frac{\pi i}{n}(p+1)}}\biggr)\biggr\}\nonumber \\
&=&2\pi i\biggl\{-\frac{a^{p}}{2na^{2n-1}}\biggl(\frac{e^{\frac{\pi i}{2n}(p+1)}(1-e^{\pi i(p+1)})}{1-e^{\frac{\pi i}{n}(p+1)}}\biggr)\biggr\}\nonumber \\
&=&2\pi i\biggl\{-\frac{a^{p}}{2na^{2n-1}}\biggl(\frac{(1-e^{\pi i(p+1)})}{e^{-\frac{\pi i}{2n}(p+1)}-e^{\frac{\pi i}{2n}(p+1)}}\biggr)\biggr\} \nonumber \\
&=&2\pi i\biggl\{\frac{a^{p}}{2na^{2n-1}}\biggl(\frac{(1-(-1)^{(p+1)})}{e^{\frac{\pi i}{2n}(p+1)}-e^{-\frac{\pi i}{2n}(p+1)}}\biggr)\biggr\}\end{eqnarray}$$ここで、$(-1)^n=\cos(\pi n)$の関係を用いて式を変形すると、
$$\begin{eqnarray}
2\pi i\biggl\{\frac{a^{p}e^{\frac{\pi i}{n}(p+1)}}{2na^{2n-1}}\biggl(\frac{(1-(-1)^{(p+1)})}{e^{\frac{\pi i}{2n}(p+1)}-e^{-\frac{\pi i}{n}(p+1)}}\biggr)\biggr\}
=\frac{a^p\pi(1+\cos(p\pi))}{2na^{2n-1}\sin(\frac{p+1}{2n}\pi)}\end{eqnarray}$$となる。従って
$$\int_{C}\frac{z^p}{z^{2n}+a^{2n}}dz=\frac{a^p\pi(1+\cos(p\pi))}{2na^{2n-1}\sin(\frac{p+1}{2n}\pi)}$$が成立する。次に、積分経路$C_{2}$を評価する。
積分$\int_{0}^{\pi}\frac{R^{p}e^{pi\theta}}{R^{2n}e^{2ni\theta}+a^{2n}}iRe^{i\theta}d\theta$の評価
$$\int_{C_2}\frac{z^p}{z^{2n}+a^{2n}}dz$$に対し、$z=Re^{i\theta}$と変数変換すると、$$\int_{C_2}\frac{z^p}{z^{2n}+a^{2n}}dz=\int_{0}^{\pi}\frac{R^{p}e^{pi\theta}}{R^{2n}e^{2ni\theta}+a^{2n}}iRe^{i\theta}d\theta$$の様になる。これから、この積分を評価していく。
$$\biggl|\int_{0}^{\pi}\frac{R^{p}e^{pi\theta}}{R^{2n}e^{2ni\theta}+a^{2n}}iRe^{i\theta}d\theta\biggr|$$を評価する。ここで、$t=e^{i\theta}$と変数変換すると $$\begin{eqnarray}
\biggl|\int_{0}^{\pi}\frac{R^{p}e^{pi\theta}}{R^{2n}e^{2ni\theta}+a^{2n}}iRe^{i\theta}d\theta\biggr|&=&
\biggl|\int_{1}^{-1}\frac{R^{p}t^{p}}{R^{2n}t^{2n}+a^{2n}}Rdt\biggr|<\biggl|\int_{1}^{-1}\frac{R^{2n-1}t^{2n-1}}{R^{2n}t^{2n}+a^{2n}}dt\biggr|\\
&=&\int_{1}^{-1}\frac{R^{2n-1}t^{2n-1}}{R^{2n}t^{2n}+a^{2n}}dt=\biggl[\frac{R^{2n-2}}{2n}\log(R^{2n}t^{2n}+a^{2n})\biggr]_{1}^{-1}=0\nonumber\end{eqnarray}$$このことから、 $$\int_{C_2}\frac{z^p}{z^{2n}+a^{2n}}dz=0$$であるので、結果
$$\int_{-\infty}^{\infty}\frac{x^p}{x^{2n}+a^{2n}}dx=\frac{a^p\pi(1+\cos(p\pi))}{2na^{2n-1}\sin(\frac{p+1}{2n}\pi)}$$となる。ここで、この式は、$p=2n-1$で$\frac{0}{0}$の不定形になってしまう
$\displaystyle\int_{-\infty}^{\infty}\frac{x^p}{x^{2n}+a^{2n}}dx$における$p=2n-1$の問題
この問題を次の様にとらえてみる。
$$\lim_{p\rightarrow2n-1}\int_{-\infty}^{\infty}\frac{x^p}{x^{2n}+a^{2n}}dx=\lim_{p\rightarrow2n-1}\frac{a^p\pi(1+\cos(p\pi))}{2na^{2n-1}\sin(\frac{p+1}{2n}\pi)}$$そして、左辺を次の様に変形する。
$$\lim_{p\rightarrow2n-1}\int_{-\infty}^{\infty}\frac{x^p}{x^{2n}+a^{2n}}dx=\lim_{p\rightarrow2n-1}\int_{-\infty}^{0}\frac{x^p}{x^{2n}+a^{2n}}dx+\lim_{p\rightarrow2n-1}\int_{0}^{\infty}\frac{x^p}{x^{2n}+a^{2n}}dx$$さらに$x=\frac{1}{t}$と変数変換すると、 $$\begin{eqnarray}
\lim_{p\rightarrow2n-1}\int_{-\infty}^{\infty}\frac{x^p}{x^{2n}+a^{2n}}dx&=&\lim_{p\rightarrow2n-1}\int_{0}^{\infty}-\frac{\frac{1}{t^{p+1}}}{\frac{1}t^{2n}+a^{2n}}dt+\lim_{p\rightarrow2n-1}\int_{\infty}^{0}-\frac{\frac{1}{t^{p+1}}}{\frac{1}t^{2n}+a^{2n}}dt\\
&=&-\lim_{p\rightarrow2n-1}\int_{0}^{\infty}\frac{\frac{1}{t^{p+1}}}{\frac{1}t^{2n}+a^{2n}}dt+\lim_{p\rightarrow2n-1}\int_{0}^{\infty}\frac{\frac{1}{t^{p+1}}}{\frac{1}t^{2n}+a^{2n}}dt\\
&=&\lim_{p\rightarrow2n-1}0=0\end{eqnarray}$$となって、$0$に収束する。次に右辺も
$$\lim_{p\rightarrow2n-1}\frac{a^p\pi(1+\cos(p\pi))}{2na^{2n-1}\sin(\frac{p+1}{2n}\pi)}=0$$に収束することを示す。
まず、$$\lim_{p\rightarrow2n-1}a^p\pi\{1+\cos(p\pi)\}=\lim_{p\rightarrow2n-1}2na^{2n-1}\sin\biggl(\frac{p+1}{2n}\pi\biggr)=0 \tag*{...$\alpha$}$$である。次に、$2n-2< p<2n$の条件下では
$$\frac{d}{dp}2na^{2n-1}\sin\biggl(\frac{p+1}{2n}\pi\biggr)=\frac{d}{dp}\sin\biggl(\frac{\pi p}{2n}+\frac{\pi}{2n}\biggr)=\frac{\pi}{2n}\cos\biggl(\frac{\pi p}{2n}+\frac{\pi}{2n}\biggr)\neq0 \tag*{...$\beta$}$$となる。さらに、$$\lim_{p\rightarrow2n-1}\frac{\frac{d}{dp} a^p\pi(1+\cos(p\pi))}{\frac{d}{dp} 2na^{2n-1}\sin(\frac{p+1}{2n}\pi)}=
\lim_{p\rightarrow2n-1}\frac{a^p\pi^{2}\sin(p\pi)}{a^{2n-1}\pi\cos\bigl(\frac{\pi p}{2n}+\frac{\pi}{2n}\bigr)}=0\tag*{...$\gamma$}$$ここで$\alpha,\beta,\gamma$は、ロピタルの定理
*4
の要件を満たしているので、今回示したかった極限の結果と一致する。従って、
$$\lim_{p\rightarrow2n-1}\int_{-\infty}^{\infty}\frac{x^p}{x^{2n}+a^{2n}}dx=\lim_{p\rightarrow2n-1}\frac{a^p\pi(1+\cos(p\pi))}{2na^{2n-1}\sin(\frac{p+1}{2n}\pi)}=0$$となる。
参考文献
[1]杉浦光夫 著『基礎数学2 解析入門I』 東京大学出版会
[2]杉浦光夫 著『基礎数学3 解析入門II』 東京大学出版会
[3]柴 雅和 著『複素関数論』 朝倉書店
[4]涌井貞美 著『道具としての複素関数』 日本実業出版社
[5]岡本和夫 著『新版数学シリーズ 新版微分積分』 実教出版
参照
$$\int_{\partial G}f(x,y)dx+g(x,y)dy=\int\int_{G}\biggl(\frac{\partial g}{\partial x}-\frac{\partial f}{\partial y}\biggr)dxdy$$証明は、参考文献[2]のp.168を参照されたい。