解釈モリモリで環論をやる イデアルの対応定理
どうも
こんにちは ごててんです 解釈モリモリで環論をやるシリーズも4本目です.
読者の想定・注意
剰余環の定義を理解しているくらいの前提です 環論やったことあります！という人はそんなの知ってるわ！という感じでムカつくと思うので読まないでください（？）
この記事は、単に環といえば「$1$を持つ可換環」を意味し, 環は自明な環でないとします！
可換代数をちょっとやったくらいの知識で個人の解釈モリモリの記事を書いています. 超的はずれなことを書いている可能性がありますが許してください. 無茶苦茶勇気を出してイメージとかそういうものを書いています（？）
この記事の目的
証明をほどほどに、イデアルの対応定理のイメージを掴むのが目的です
厳密さ等を伴わないイメージを書くこともあるので苦手な方はブラウザバック推奨です
自然な準同型
イデアルの対応定理を説明する前に, 「自然な準同型」を説明します. 本来は準同型を定義してから説明するべきですが, せずに説明します.
$A$を環, $I$をイデアルとするとき, 写像$\pi : A \rightarrow A/I$を$\pi(a)=a+I$で定める. これを自然な準同型という.
「自然な」「準同型」両方よく分かりませんね. とりあえずは意味を疑わずに行きましょう......
写像としてはかんたんです. $a$から$a+I$に対応させるというだけです. またこれは全射になります.
証明はしませんが, 次の命題が成立します. この命題が一つのキーとなります.
$A$を環, $I$をイデアル, $J$を$I$を含むイデアルとするとき, $\pi(J)$は$A/I$のイデアル.
一般に, イデアルの像がイデアルとなるわけではありません. 適切な仮定（全射準同型）のもとなら成立します.
$\pi(J)$とは何者でしょうか. これは$J/I$と書かれることが多いです. なぜなら, $x \in J$とするときの$x+I$を集めてきているからです.
観察をば
例を見てみましょう.
$\pi : \mathbb{Z} \rightarrow \mathbb{Z} / 12 \mathbb{Z}$を自然な準同型とする. たとえば$\pi(3 \mathbb{Z})=3\mathbb{Z} / 12\mathbb{Z}$はイデアルとなる.
$\mathbb{Z} / 12 \mathbb{Z}$を少し観察したいと思います. $\mathbb{Z} / 12 \mathbb{Z}$のイデアルを列挙してみましょう. これは次のようになります.
・$\mathbb{Z} / 12 \mathbb{Z} = \pi(\mathbb{Z})$
・$2\mathbb{Z} / 12 \mathbb{Z} = \pi(2\mathbb{Z})$
・$3\mathbb{Z} / 12 \mathbb{Z} = \pi(3\mathbb{Z})$
・$4\mathbb{Z} / 12 \mathbb{Z} = \pi(4\mathbb{Z})$
・$6\mathbb{Z} / 12 \mathbb{Z} = \pi(6\mathbb{Z})$
・$12\mathbb{Z} / 12 \mathbb{Z} = \pi(12\mathbb{Z})$
よく見ると, すべて$12\mathbb{Z}$を含むイデアルの像として書けています. さらに言えば, $12\mathbb{Z}$を含むイデアルは$\mathbb{Z},2\mathbb{Z},3\mathbb{Z},4\mathbb{Z},6\mathbb{Z},12\mathbb{Z}$の$6$個だけです. そしてこれは偶然ではありません.
イデアルの対応定理とは
さて, もうイデアルの対応定理を説明できます. これは「剰余環とは何か」に迫る一つのカギです.
$A$を環, $I$をイデアルとし, $A/I$のイデアル全体を$X$, $A$の$I$を含むイデアル全体を$Y$とする. このとき2つの写像を定める.
・$\phi : X \rightarrow Y$を$\overline{J} \mapsto \pi^{-1}(\overline{J})$で定める.
・$\psi : Y \rightarrow X$を$J \mapsto \pi(J)$で定める.
すると, この2つの写像は互いに逆写像となる.
まあ記号とか集合とかを用意して正確に述べましたが, 実際に運用するなら下くらいの理解で大丈夫だと思います.
$A/I$のイデアルは$A$の$I$を含むイデアルと1対1に対応する.
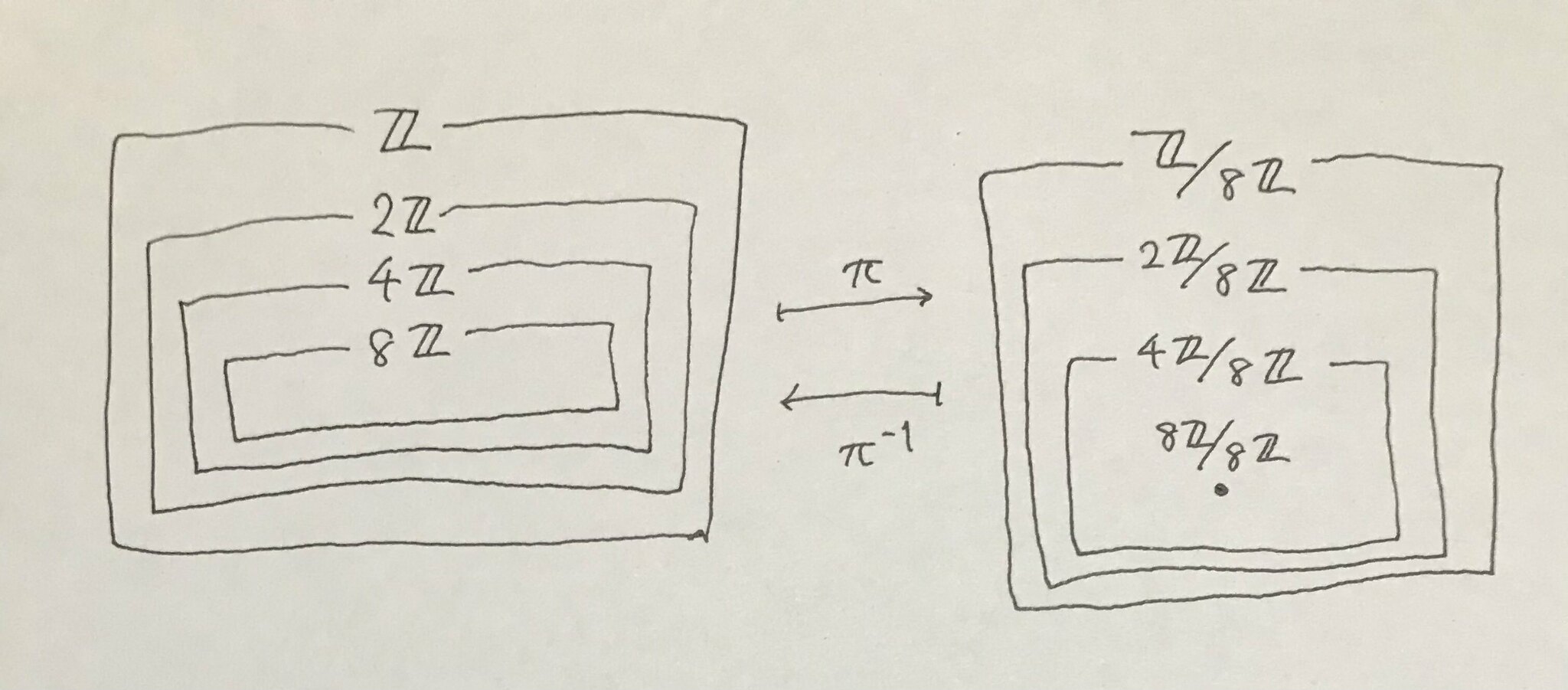とりあえず描いた図
例題で覚えよう
$\mathbb{Q}[X] / (X)$のイデアルを列挙せよ.
これは実質的に, $\mathbb{Q}[X]$の$(X)$を含むイデアルを列挙すればいい問題です.
$(X)$を真に含むイデアル$I$を考えると, 定数項を持つ元が入っているはずです.（定数項がない元はすべて$X$で割り切れるため, $(X)$に含まれる.）さて, 定数項を持つ元を$f(X) \in I$とすると, 多項式の割り算をして$f(X) = Xg(X)+a$$(g(X) \in \mathbb{Q}[X], a \in \mathbb{Q},a \ne 0)$と書くことができます. ということは, $a = f(X) - Xg(X) \in I$が成立します. （$(X) \subset I$より$Xg(X) \in I$.）これはつまり, $I$は可逆元を含むことになります.（$0$でない有理数は$\mathbb{Q}[X]$の有理数.）可逆元を含むイデアルは全体に一致するので, $I=\mathbb{Q}[X]$が成立します.
ということは, $\mathbb{Q}[X]$の$(X)$を含むイデアルは$(X), \mathbb{Q}[X]$のみです. ここからイデアルの対応定理を使ってわかることは, $\mathbb{Q}[X] / (X)$のイデアルは$\mathbb{Q}[X] / (X) , (X) / (X)$のみだということです. イデアルが, 自分自身と$(0)$しかないということから, これが体だということまでわかりました！
もう少し踏み込んだ言語化
冒頭の注意で個人の解釈モリモリの記事と書きましたが, この見出しは特に個人の解釈がものすごいです. そう......かな？くらいで読んでください.
イデアルの対応定理を踏まえてイデアルを見直してみましょう. イデアルは, ある意味で「倍数」と見ることができました. そしてイデアルで割るということは, イデアルの対応定理から, 環のイデアルをごっそり減らすということだと分かりました.
ということは, 無茶苦茶大きいイデアルで割れば大量にイデアルを削ることができます. さて, これ以上大きくできない！というほど大きいイデアルで割ると, イデアルが限界まで少なくなった剰余環を得ることができます. イデアルが限界まで少ないということは, 「倍数」の概念がつまらなくなるということで, つまり体になってしまいます.
この, 限界まで大きくなったイデアルを極大イデアルと呼びます. この記事では扱いません.
おつかれさまでした
剰余環とは何か, に迫るカギとなる対応定理を説明しました. イデアルを見ればどんな環なのか理解が深まる, ということで, 剰余環のイデアルがわかるというこの定理は剰余環への理解を大きく深めるものだと思います. ここまで読んでいただきありがとうございました.