反転を知る人のためのトレミーの定理の証明方法
この記事は,「 反転を知らない人のためのトレミーの定理の証明方法 」とは異なります.
はじめに
円$\Gamma$上の(凸)四角形$ABCD$について、
$$AB \cdot CD + BC \cdot DA = AC \cdot BD$$
 トレミーの定理
トレミーの定理
トレミーの定理は反転で証明しなければならない。
トレミーの定理の証明は、反転以外認められないということが広く知られています。
では,等角共役線を引く方法は許されないのしょうか?
もちろんそんなことはありません!
証明
反転する
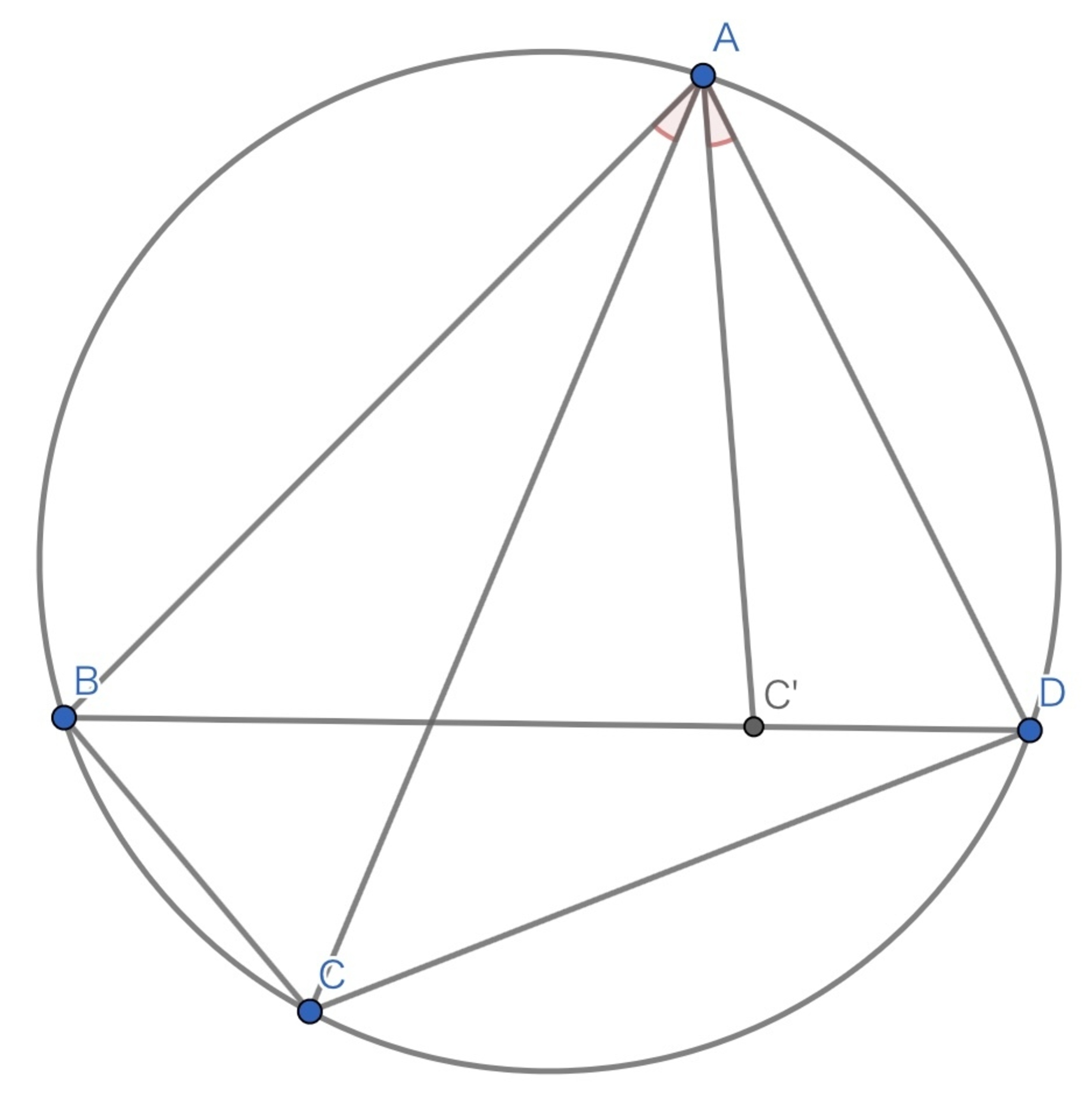
中心$A$,半径$\sqrt{AB \cdot AC}$の円による反転の写像と,$\angle BAD$の二等分線による対称移動の写像の合成を$f$とします.
$f(B)=D$,$f(D)=B$より,$f$による円$\Gamma$の像$f[\Gamma]$は直線$BD$です.
$f$は,$A$を通る直線をその等角共役線にうつすので,$f(C)$は,直線$AC$の等角共役線と直線$BD$の交点です.
直線$AC$およびその等角共役線は$\angle BAD$の内部にあるので,直線$BD$とは$2$点$B,D$の間で交わります.
すなわち,$f(C)B + Df(C)= BD$です.
長さの変換
$A$と異なる任意の$2$点$X,Y$に対し,
$$XY = f(X)f(Y) \cdot \dfrac{AB \cdot AD}{Af(X) \cdot Af(Y)}$$
$$CD = f(C)f(D) \cdot \dfrac{AB \cdot AD}{Af(C) \cdot Af(D)} = f(C)B \cdot \dfrac{AB \cdot AD}{Af(C)} \div AB$$
$$BC = f(B)f(C) \cdot \dfrac{AB \cdot AD}{Af(B) \cdot Af(C)} = Df(C) \cdot \dfrac{AB \cdot AD}{Af(C)} \div AD$$
$$AC = \dfrac{AB \cdot AD}{Af(C)}$$
これを用いて,主張から点$C$を消去すると,
$$f(C)B \cdot \dfrac{AB \cdot AD}{Af(C)} + Df(C) \cdot \dfrac{AB \cdot AD}{Af(C)} = BD \cdot \dfrac{AB \cdot AD}{Af(C)}$$
です.
両辺を$\dfrac{AB \cdot AD}{Af(C)}$で割ります.
トレミーの定理は以下と同値
$$f(C)B + Df(C)= BD$$
前の節の最後で確認したとおり,これは成立します.
これでトレミーの定理が証明されました!
補足
以上の証明を,
反転を知らない人
向けに書き直したもの,すなわち,「反転を知らない人のための反転を知る人のためのトレミーの定理の証明」が,
よく知られた
証明になります.
つまり,「補助線が天下りすぎる」「反転で証明しろ」などと散々言われてきた(*誰によって?*)あの証明も,明示的に反転が登場するわけではありませんが,やっていることは反転なので,実はトレミーの定理の証明として適切でした.