数の落とし子「距離空間⑥⑦」の補足
YouTubeチャンネル「 数の落とし子 」の動画の補足です。
背景
私は工学系出身ですが趣味として大学数学を勉強中で、「数の落とし子」チャンネルの距離空間と位相空間の動画を視聴しています。その中の 距離空間⑦ では定理5として連続写像の同値表現として開集合を使った同値表現を学びました(Mathlogで番号を変える方法がわかりませんでした)。
$f:X \to Y$は連続写像である $\iff$ $\forall A \in \mathscr{O}_Y$に対し、$f^{-1}(A) \in \mathscr{O}_X$
$\mathscr{O}_Y$は$Y$側の開集合全体の集合の意味です。同値なものの否定を取っても同値ですから、以下のことがわかります。
$f:X \to Y$は連続写像ではない $\iff$
$\exists A \in \mathscr{O}_Y$ s.t. $f^{-1}(A) \notin \mathscr{O}_X$ $\iff$
$\exists A \in \mathscr{O}_Y$ s.t. $f^{-1}(A) \cap \partial (f^{-1}(A)) \neq \emptyset$
3行目は「$Y$側の開集合で$f$による逆像が境界点を含むようなものが存在する」という意味です。
具体例
以下のような階段関数$f:\mathbb{R}\to\mathbb{R}$を考えると、開区間$A$の逆像$f^{-1}(A)$が開区間でないことがわかります。
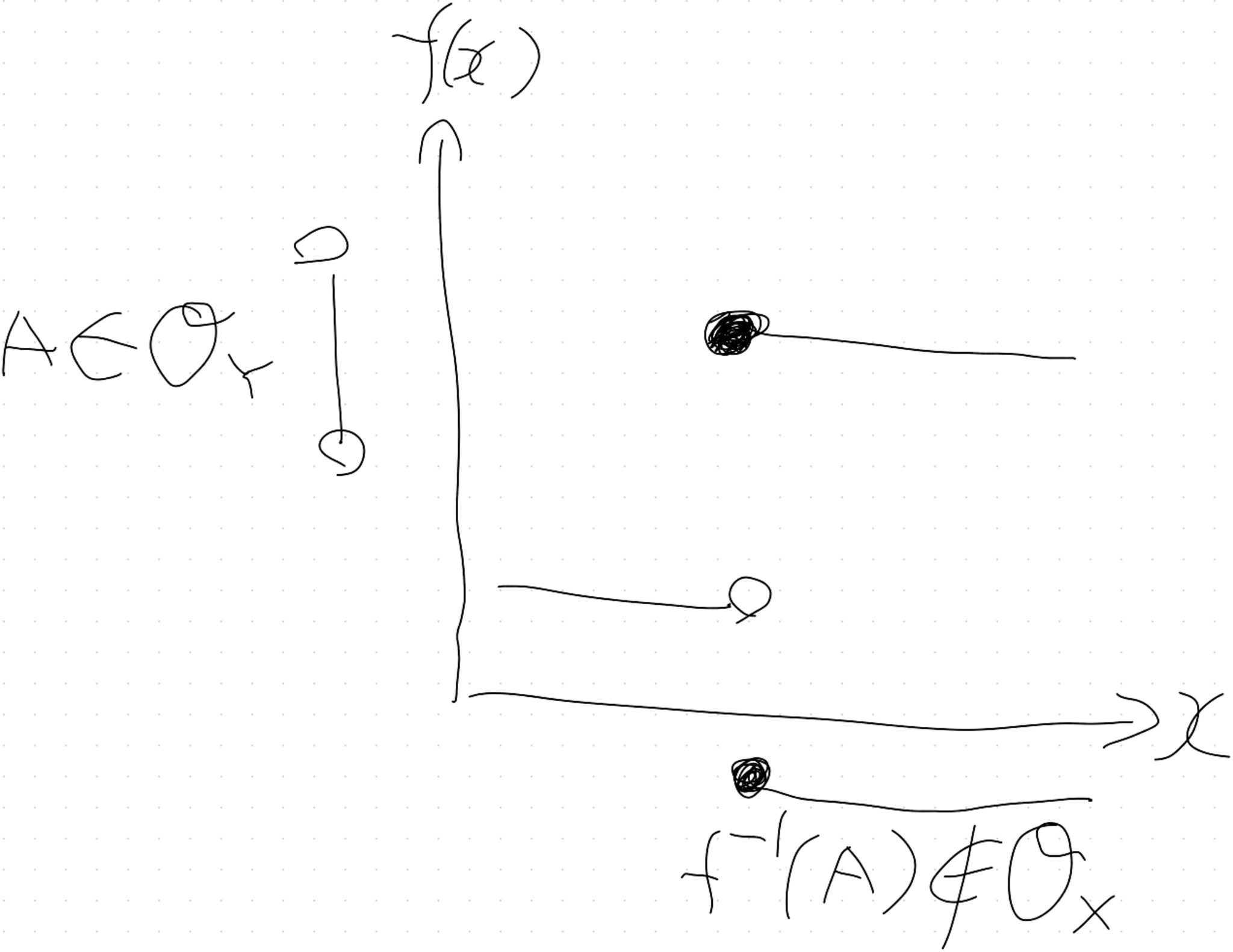
このとき下側の●で表されるのが、$f^{-1}(A)$の境界点です。
予想
ここで私は「そのような境界点は$f$が不連続となる点と一致するのではないか?」と考え、次のように予想しました。
$f: X \to Y$ が $x_0 \in X$ で連続ではない $\iff$ $\exists A \in \mathscr{O}_Y$ s.t. $x_0 \in f^{-1}(A) \cap \partial (f^{-1}(A))$
右辺は「$Y$側の開集合で$f$による逆像が点$x_0$を境界点として含むものが存在する」という意味です。
なお 距離空間⑥ で$f$が点$x_0$で連続であることの他の同値表現を学びましたので、これを使います。
$f:X \to Y$ は $x_0 \in X$ で連続である $\iff$ $\forall A \in \mathscr{N}_Y(f(x_0))$ に対し、$f^{-1}(A) \in \mathscr{N}_Y(x_0)$
$\mathscr{N}_Y(y)$は$Y$側の点$y$の近傍の意味です。
準備
証明に入る前に、予想の左辺と右辺を内点の言葉を使った同値表現に書き換えておきましょう。まず左辺は定理2と近傍の定義を使って、次のように書き換えます。
$f: X \to Y$ が $x_0 \in X$ で連続ではない $\iff$
任意の$A \in \mathscr{N}_Y(f(x_0))$に対し$f^{-1}(A) \in \mathscr{N}_Y(x_0)$とは限らない $\iff$
$\exists A \in \mathscr{N}_Y(f(x_0))$ s.t. $f^{-1}(A) \notin \mathscr{N}_Y(x_0)$ $\iff$
$\exists A\subset Y$ s.t. $f(x_0) \in I(A)$ かつ $x_0 \notin I(f^{-1}(A))$
ここで$I(A)$は$A$の内点集合です。同様に予想の右辺も開集合の定義、逆像の定義、境界点の性質をそれぞれの項に使って書き換えます。
$\exists A \in \mathscr{O}_Y$ s.t. $x_0 \in f^{-1}(A) \cap \partial (f^{-1}(A))$ $\iff$
$\exists A \subset Y$ s.t. $I(A)=A$ かつ $f(x_0) \in A$ かつ $x_0 \notin I(f^{-1}(A))$
第3項の変形は、$\implies$に境界点は内点ではないことを、$\impliedby$にある集合に含まれる点がその集合の内点ではないならば境界点であることを利用しました。
証明
最初の予想を内点の言葉を使って書き換えると、証明がかなり簡単になりました。
$\exists A\subset Y$ s.t. $f(x_0) \in I(A)$ かつ $x_0 \notin I(f^{-1}(A))$ $\iff$
$\exists A\subset Y$ s.t. $I(A)=A$ かつ $f(x_0) \in A$ かつ $x_0 \notin I(f^{-1}(A))$
まず$\impliedby$を示す。ある$A \subset Y$が存在して、$I(A)=A$ かつ $f(x_0) \in A$ かつ $x_0 \notin I(f^{-1}(A))$を満たすと仮定すると、仮定より$f(x_0) \in A = I(A)$ なので $f(x_0) \in I(A)$、すなわち$\impliedby$が示された。
次に$\implies$を示す。ある$A \subset Y$が存在して、$f(x_0) \in I(A)$ かつ $x_0 \notin I(f^{-1}(A))$ を満たすと仮定する。ここで$B=I(A)$とおくと、まず$I(B)=I(I(A))=I(A)=B$と$f(x_0) \in I(A)=B$は明らか。次に$I(A) \subset A$ なので $I(f^{-1}(I(A))) \subset I(f^{-1}(A))$ が成り立ち、更に$x_0 \notin I(f^{-1}(A))$なので$x_0 \notin I(f^{-1}(I(A))) = I(f^{-1}(B))$が成り立つ。まとめると$\exists B\subset Y$ s.t. $I(B)=B$ かつ $f(x_0) \in B$ かつ $x_0 \notin I(f^{-1}(B))$となるが、これは$B$を$A$に読み替えれば結論そのものである。以上より$\implies$が示された。
まとめ
$f$が$x_0$で連続でないことと、$Y$側の開集合で逆像が$x_0$を境界点として含むものが存在することが同値であることを証明しました。
$f: X \to Y$ が $x_0 \in X$ で連続ではない $\iff$ $\exists A \in \mathscr{O}_Y$ s.t. $x_0 \in f^{-1}(A) \cap \partial (f^{-1}(A))$
両辺の否定を取れば、$f$が$x_0$で連続であることと、$Y$側の開集合で逆像が$x_0$を境界点として含むものが存在しないことが同値であることがわかります。
$f: X \to Y$ が $x_0 \in X$ で連続である $\iff$ $\forall A \in \mathscr{O}_Y$ s.t. $x_0 \notin f^{-1}(A) \cap \partial (f^{-1}(A))$
つまり$x_0$が逆像$f^{-1}(A)$に含まれないか、逆像の内点として含まれるかのどちらかということですね。
初めてMathlogの記事を書きましたが、これは大変ですね! 間違いなどありましたらコメントお願いします。
