機械学習に関する数理1
バックプロパゲーションを理解しよう
んちゃ！
今回は機械学習の入門的記事としてバックプロパゲーションについて書いていくのだ。
ちなみに、いつも通り厳密性より分かるを重視しているので、「どんなものでも厳密でなければならぬ！」と考えている方はブラウザバック推奨なのだ。
ニューラルネットワークの構成
層とは次のようなものなのだ。入力$\mathbb{x}\in\mathbb{R}^{m}$、重み$\mathbb{W}\in\mathbb{R}^{m}\times \mathbb{R}^{n}$、バイアス$\mathbb{b}\in\mathbb{R}^{n}$、非線形関数列$\mathbb{f}=\{f_{i}\}_{i=1,2,...,n}$、出力$\mathbb{y}\in\mathbb{R}^{n}$とするとき、次の様な処理を行うものの事なのだ。
\begin{equation}
\mathbb{y}=\mathbb{f}(\mathbb{x}\mathbb{W}+\mathbb{b})
\end{equation}
ただし、$\mathbb{f}(*)$とは成分で書くと次の様に定義されているのだ。
\begin{equation}
y_{i}=f_{i}(\sum_{j}^{m}x_{j}W_{ji}+b_{i})
\end{equation}
ちなみに、以下重み$\mathbb{W}$、バイアス$\mathbb{b}$、非線形関数列$\mathbb{f}$の層を$L(\mathbb{W},\mathbb{b},\mathbb{f})$の様に書くことにするのだ。
NewuralNetworkとは、層$L_{i}(\mathbb{W}_{i},\mathbb{b}_{i},\mathbb{f}_{i})\quad (i=1,2,...,N)$を接続して処理を行ったものなのだ。
バックプロパゲーション
ベクトル場$\mathbb{f}:\mathbb{R}^{m}\rightarrow\mathbb{R}^{n}$の$\mathbb{x}\in\mathbb{R}^{m}$でのTaylor展開は次の様に書けるのだ。
\begin{equation}
\mathbb{f}(\mathbb{x}+\mathbb{\epsilon})=\sum_{k=0}^{\infty}\frac{(\mathbb{\epsilon}\cdot \nabla)^{k}}{k!}\mathbb{f}(\mathbb{x})
\end{equation}
\begin{eqnarray} \mathbb{f}_{i}(\mathbb{x}+\mathbb{\epsilon}t)&=&g(t)\\ &=&\sum_{k=0}^{\infty}\frac{1}{k!}\frac{d^{k}}{dx^{k}}g(0)\\ &=&\sum_{k=0}^{\infty}\frac{(\mathbb{\epsilon}t\cdot\nabla)^{k}}{k!}\mathbb{f}_{i}(\mathbb{x}) \end{eqnarray}
パラメータ$\mathbb{a}=(a_{1},a_{2},...,a_{N})$を持つスカラー関数$f(a_{1},a_{2},...,a_{N}):\mathbb{R}^{n}\ni\mathbb{x}\rightarrow f(a_{1},a_{2},...,a_{N};\mathbb{x})\in\mathbb{R}$を極小にするパラメータは次のような方法を続ける事で近似できるのだ。
\begin{equation}
\mathbb{a}\rightarrow\mathbb{a}-\lambda\nabla_{\mathbb{a}}f(\mathbb{a},\mathbb{x}) \quad(\lambda\in\mathbb{R}_{+}かつ\lambdaは十分小ならしめる正数)
\end{equation}
$\mathbb{\epsilon_{a}}\in\mathbb{R}^{N}$を考えると
\begin{equation}
f(\mathbb{a}-\lambda\mathbb{\nabla}_{\mathbb{a}}f(\mathbb{a},\mathbb{x}),\mathbb{x})\simeq f(\mathbb{a},\mathbb{x})-\lambda||\mathbb{\nabla}_{\mathbb{a}}f(\mathbb{a},\mathbb{x})||^{2}
\end{equation}
と書けるので、$||\lambda\mathbb{\nabla}_{\mathbb{a}}f(\mathbb{a},\mathbb{x})||^{2}\geq 0$なので、かならず負の値になるからなのだ。
実数$x\in\mathbb{R}$から実ベクトル$\mathbb{v(x)}=(F_{1}(x),F_{2}(x),...,F_{n}(x))\in\mathbb{R}^{n}$への関数と、目的関数$E:\mathbb{R}^{n}\rightarrow \mathbb{R}$を考えるのだ。この時、$\frac{dE}{dx}$は次の様に書けるのだ。
\begin{equation}
\frac{dE}{dx}=\sum_{k=1}^{n}\frac{dF_{k}}{dx}\frac{\partial E}{\partial F_{k}}
\end{equation}
\begin{eqnarray} \frac{dE}{dx}&=&\lim_{\Delta x\rightarrow 0}\frac{1}{\Delta x}[E(F_{1}(x+\Delta x),F_{2}(x+\Delta x),...,F_{n}(x+\Delta x))-E(F_{1}(x),F_{2}(x+\Delta x),...,F_{n(x+\Delta x)})\\ &+&E(F_{1}(x),F_{2}(x+\Delta x),...,F_{n}(x+\Delta x))-E(F_{1}(x),F_{2}(x),...,F_{n}(x+\Delta x))\\ &+&\cdots \\ &+&E(F_{1}(x),F_{2}(x),...,F_{n}(x+\Delta x))-E(F_{1}(x),F_{2}(x),...,F_{n}(x))]\\ &=&\sum_{k=1}^{n}\frac{dF_{k}}{dx}\frac{\partial E}{\partial F_{k}} \end{eqnarray}
先の微分で$\frac{dF_{k}}{dx}\quad (k=1,2,...,n)$を自己微分列、$\frac{\partial E}{\partial F_{k}}\quad (k=1,2,...,n)$を目的微分列と呼ぶことにするのだ。
＊自己微分列、目的微分列なる様な用語は一般的に使われていないので注意。この記事の中だけで通じる用語です。目的微分は誤差関数を入力xで微分したもの。勾配降下法ではこの微分したものが最も重要なことが分かるだろうなのだ。
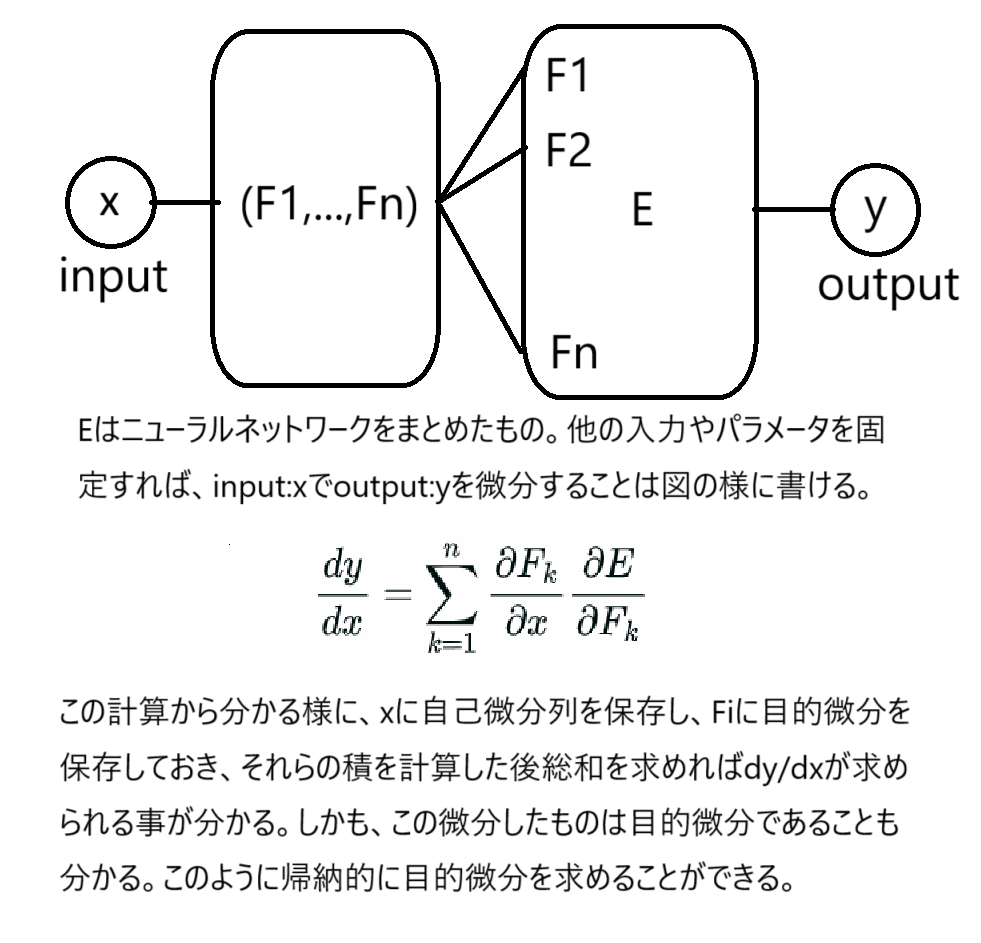
チェインルールを考慮すると下記画像の様にして目的微分を求める事ができる。
画像の名前
つまり、グラフ的に考えると次の様に目的微分を求めることで、すべての頂点に対して目的微分を求めることができるのだ。
- まず各頂点について、自己微分を求める処理を行う。
- 出次元が0の頂点について目的微分を求めるのだ。
- 次に、これら頂点に隣接する頂点を抜き出し、各々頂点を始点側の自己微分列、終点側の目的微分列との内積を求めるのだ。
- 以下同様の操作を繰り返すのだ。
- この操作が完了すれば各頂点上の目的微分が求められるのだ。
- ゆえに、パラメータを入力ととらえれば、これに対する目的微分も求められるので、勾配降下法を用いてパラメータを変更し、誤差関数を減少させることができるのだ。
- この勾配降下法を用いることで誤差関数の極小値を求めることができるのだ。
この記事を高評価した人
この記事に送られたバッジ
投稿者
