文献あり

アステカダイヤモンドの敷き詰め

405

はじめに

位数$n$のアステカダイヤモンドとは, 領域$|x|+|y|\leq n+1$に含まれる$1\times 1$の正方形の合併のことをいいます. これを$1\times 2$の長方形(ドミノ)で敷き詰めていくことを考えます.
位数!FORMULA[4][36584004][0]のアステカダイヤモンド位数$n=3$のアステカダイヤモンド
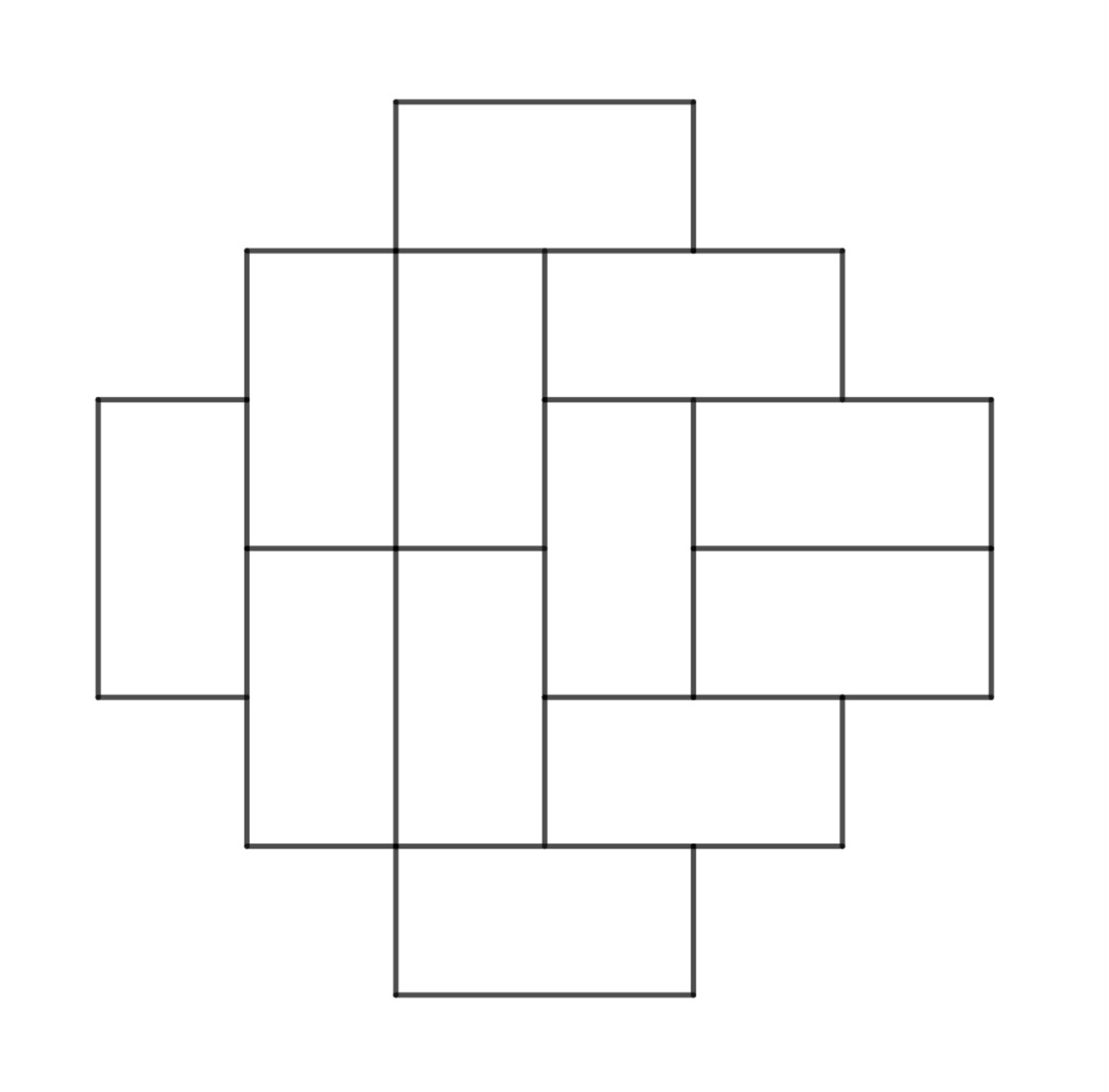ドミノで敷き詰め
実は, 位数$n$のアステカダイヤモンドをドミノで敷き詰める方法の総数は$2^{\frac{n(n+1)}{2}}$通りであることが知られています. シンプルで綺麗な結果ですね！今回はこの記事でその証明をしていきたいと思います.

証明の方針

①とある経路とドミノでの敷き詰めを一対一対応させる
②一対一対応させた経路の数を数え上げる

証明

①一対一対応

ドミノ$\to$経路

与えられたドミノでの敷き詰めを, 経路(の組)に変換することを考えます. 具体的には、次のようにします:

$1.$図3のように, アステカダイヤモンドの下半分の部分のうち, 左側の辺すべてに点をつける(これらを始点とする経路を描く).
$2.$図4のような方法で, 右側の辺に到達するまで矢印を引く.

先ほどの敷き詰めの例を使うと, 図5のような経路を得ることが出来ます.

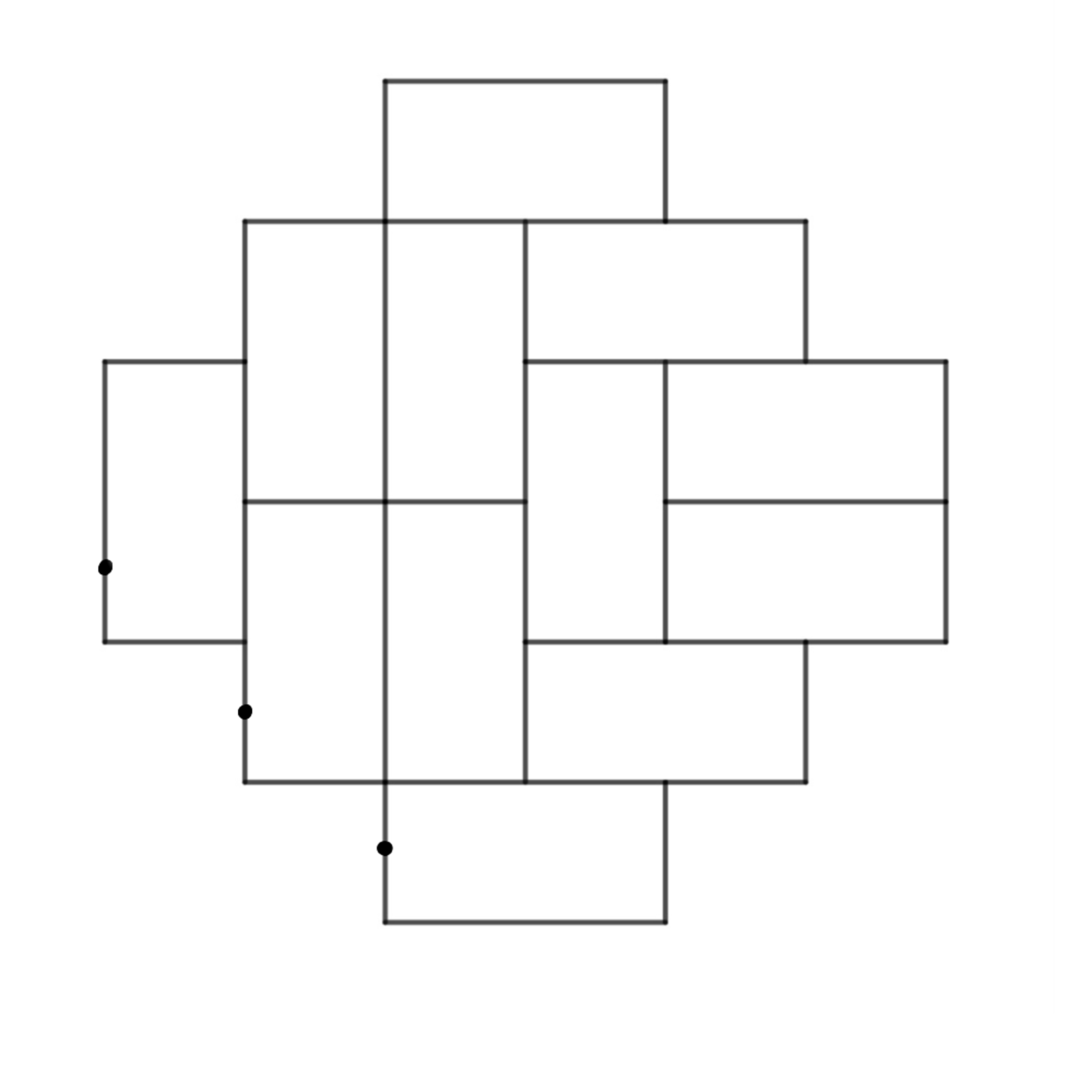始点
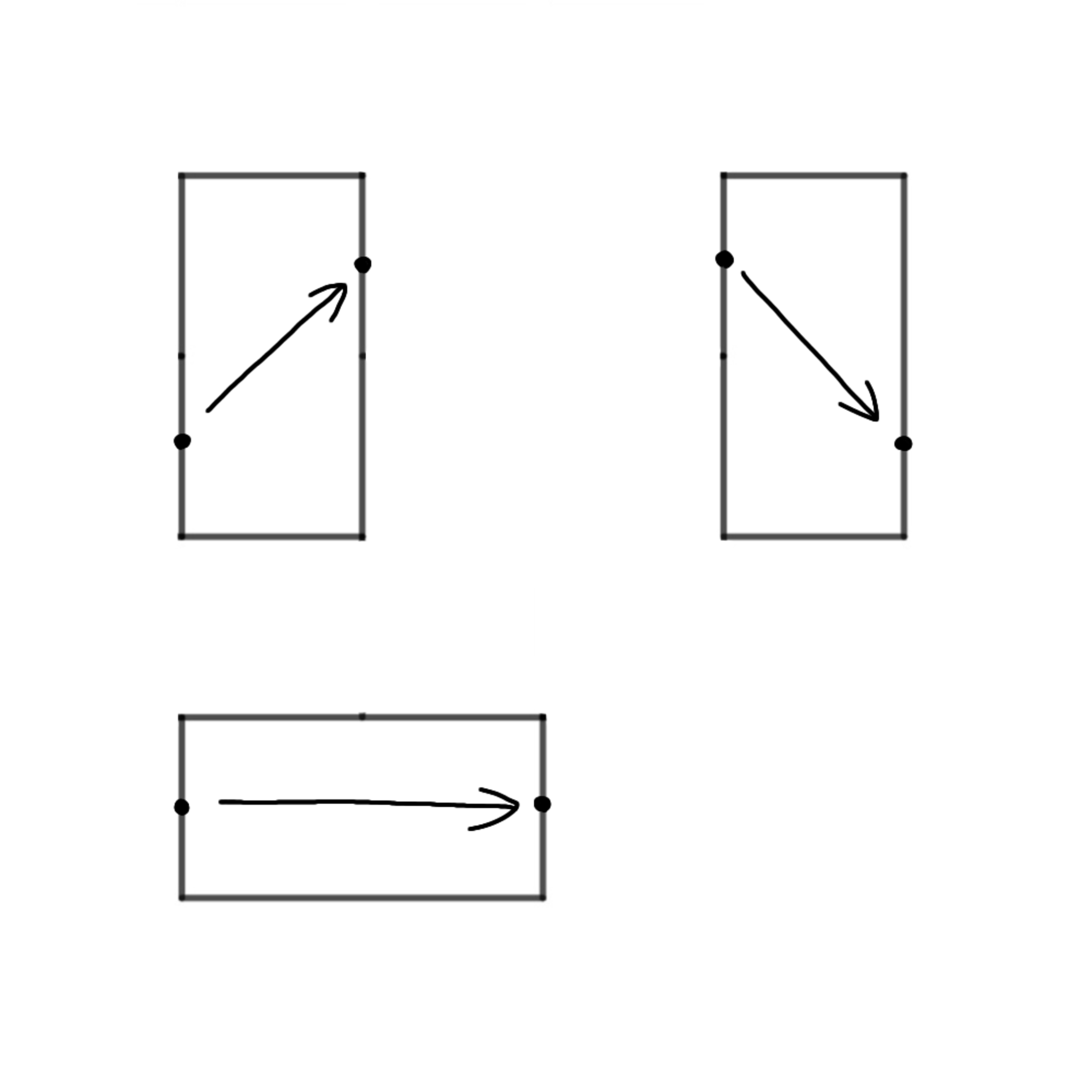矢印の引きかた
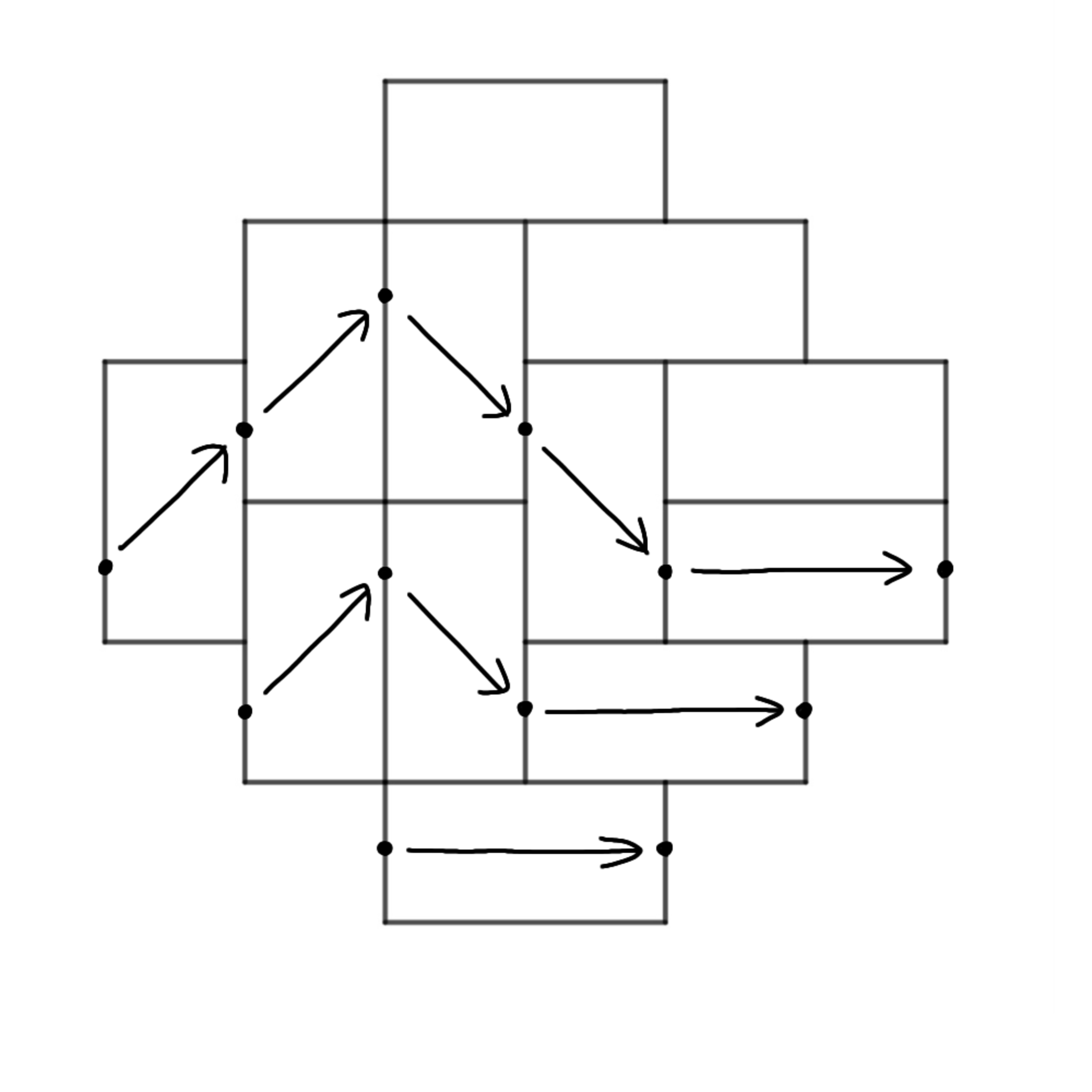経路の例

さらに, アステカダイヤモンドを図6のように市松模様で塗り分けると, 経路上の点は全て色付きのマスの左側の辺($=$白いマスの右側の辺)の上にのっていることが分かります.
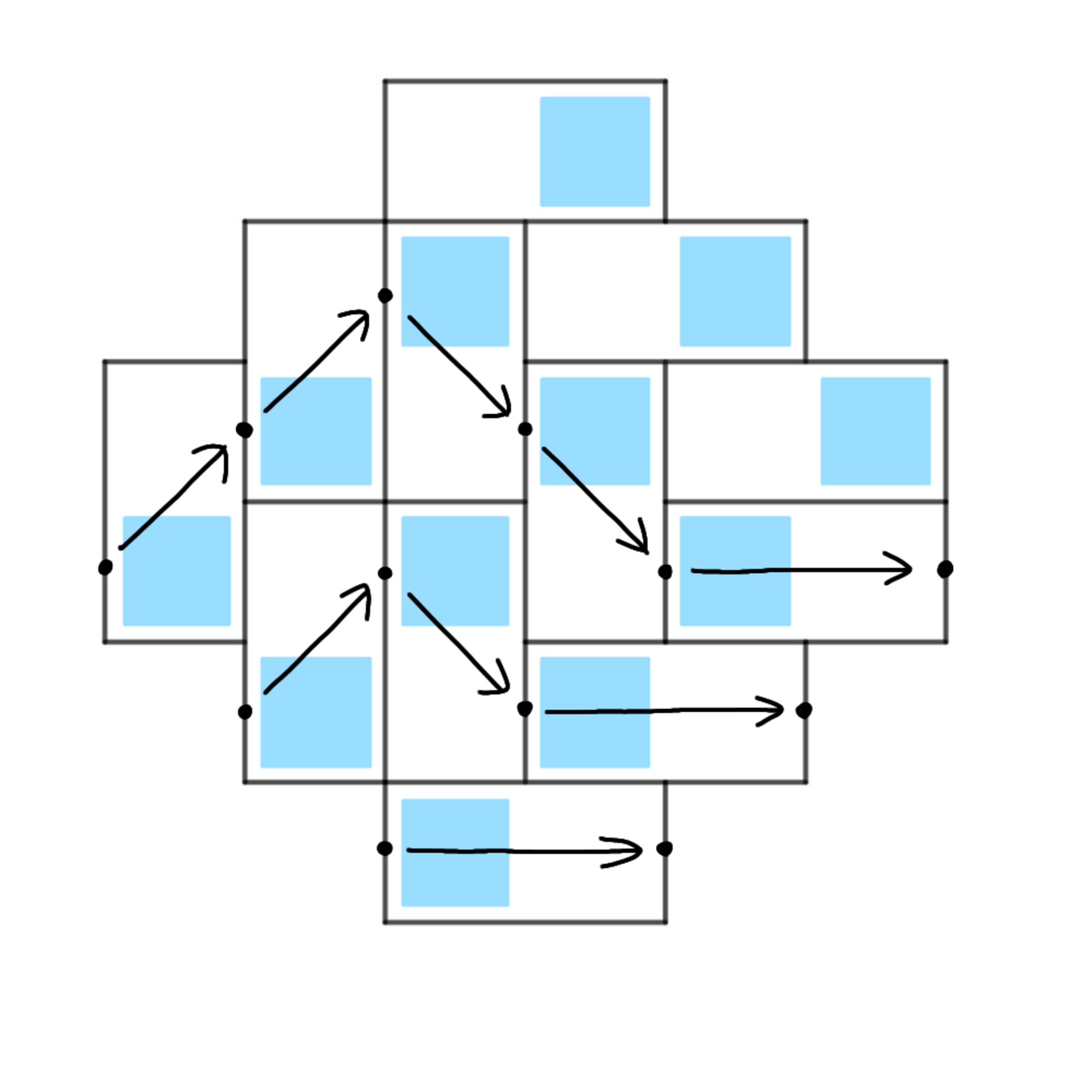市松模様

加えて, これらの経路は決して交差しないことが分かります. (ふたつの経路が交差するとは, 経路が同じ点を共有することをいいます. 交差すると仮定すると, 図7の示すいずれかの状況になる必要がありますが, それはどれも不可能です. )

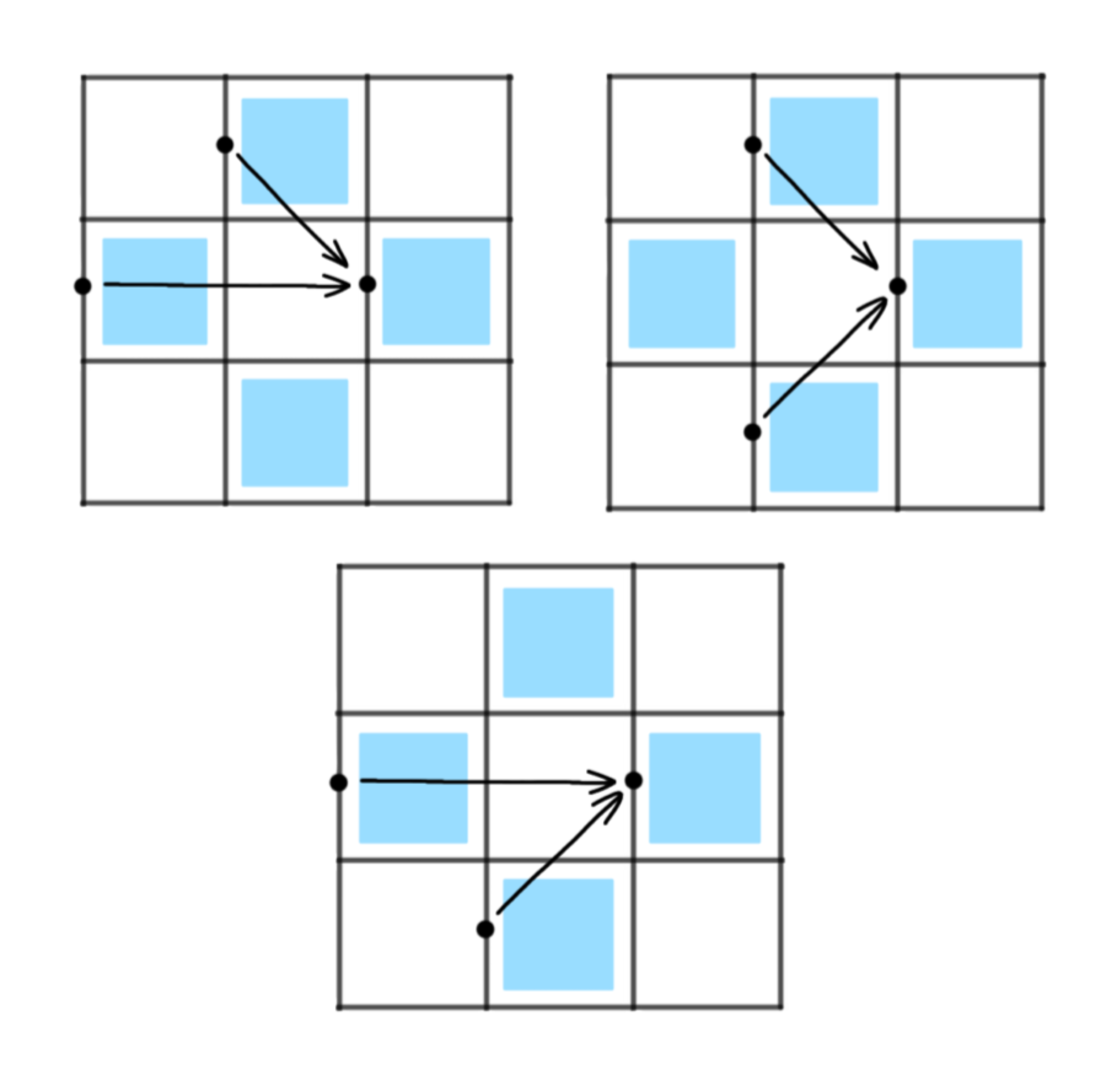このようにはならない

経路$\to$ドミノ

逆に, アステカダイヤモンドに対して

・始点を図3のように定め
・$x$方向, $y$方向への移動がそれぞれ$(x,y)=(1,1),(2,0),(1,-1)$のいずれかになるように
・経路同士が交差しないように

経路を書き込むと, その経路から一意にドミノの敷き詰めを定めることができます.

証明

まず, 経路は交差しないので, 書き込んだ経路が通るマスにはドミノを一意に敷き詰めることができます. したがって, 経路が書き込まれていないマスにドミノを一意に敷き詰められることが言えればいいわけです. ここで, 経路が色付きのマスを通ることと経路がその一つ左の白いマスを通ることが(始点・終点以外の位置で)同値であることより, 経路が書き込まれていないマスは, 左が白いマスで右が色付きのマスである横倒しのドミノで敷き詰められることが分かります. これ以外のドミノを少なくともひとつ使って経路が通らないマスを敷き詰められたと仮定すると, そのドミノから図4のルールに従って左右に経路を伸ばしていけば, 結局このドミノはいずれかの経路に組み込まれてしまうことになり, 矛盾します.以上より経路からドミノの敷き詰めが一意に決まることが示されました.

以上より, 条件をみたす非交差経路の組の数を数える問題に帰着することができました！

②経路の数え上げ

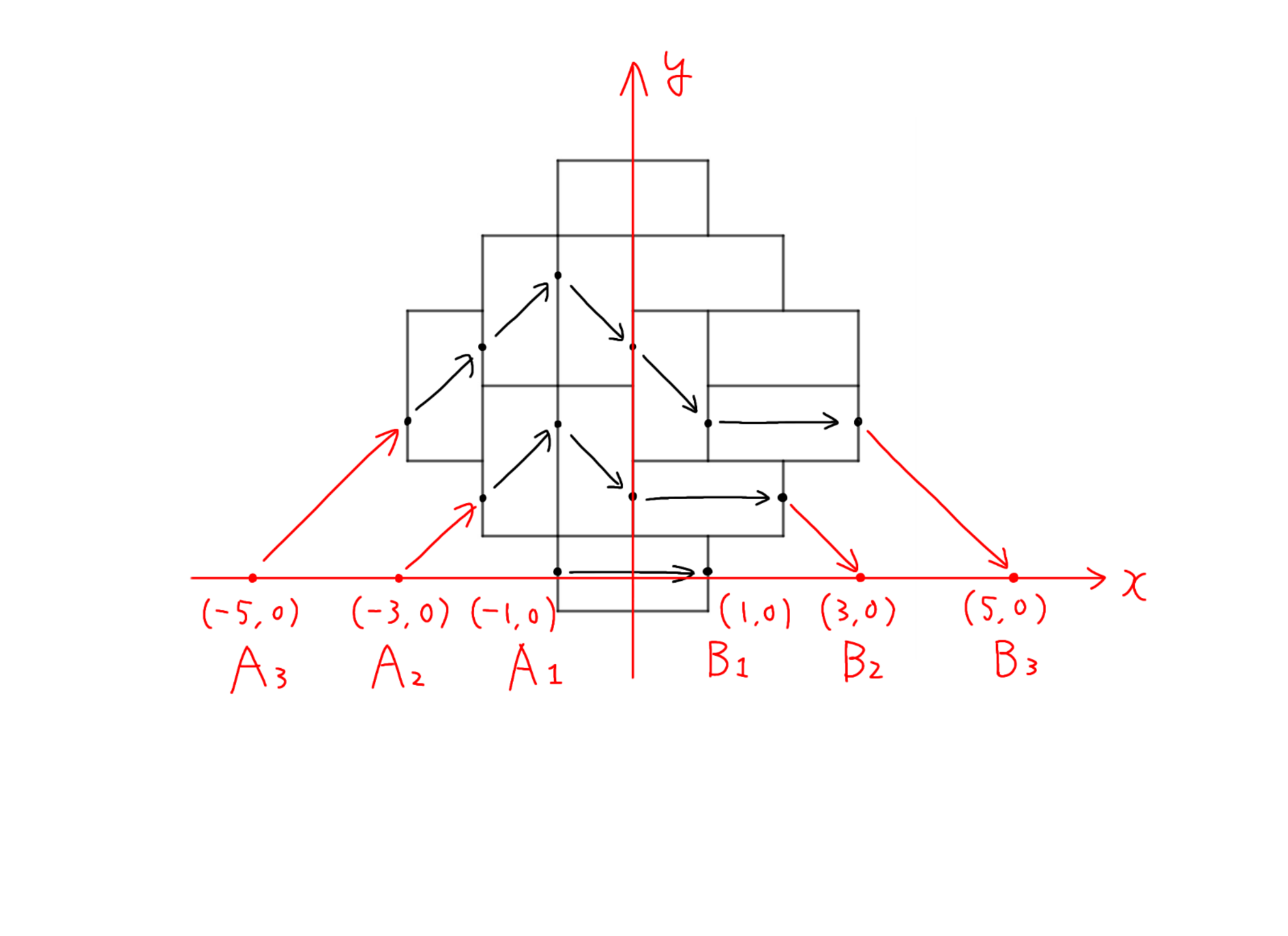非交差経路

図8のように, 最下段のマスを通るように$x$軸を, 図形の左右の対称軸に$y$軸をとり, $i=1,2,\cdots,n$について点$A_i$および$B_i$をそれぞれ$(-2i+1,0),(2i-1,0)$で定めます. ここで, $A_i$から$B_i$へ向かう経路であって

(i)$x$軸を下回らない
(ii)$x$方向、$y$方向への移動がそれぞれ$(x,y)=(1,1),(2,0),(1,-1)$のいずれかである

の条件を満たす経路を$\pi_i$とし, 非交差経路の組$(\pi_1, \pi_2, \cdots, \pi_n)$全体の集合を$\Pi_n$とすると, ①の考察より$|\Pi_n|$が求めるべきものです. また, $(0,0)$から$(2n, 0)$へ向かう経路であって, (i)と(ii)の条件をどちらも満たすものの総数を$r_n$で表します(この$r_n$をlarge Schröder numberと呼びます).

さらに, (i)と(ii)に加えて

(iii)$x$軸上で$(x,y)=(2,0)$の移動を行わない

の条件を満たして$A_i$から$B_i$へ向かう経路を$\omega_i$とし, 非交差経路$(\omega_1, \omega_2, \cdots, \omega_n)$全体の集合を$\Omega_n$とします. また, $(0,0)$から$(2n,0)$へ向かう経路であって(i)(ii)(iii)の条件をすべて満たすものの総数を$s_n$で表します(この$s_n$をsmall Schröder numberと呼びます).

ここでいくつかの補題を用意します:

$|\Omega_{n+1}|=|\Pi_n|$

!FORMULA[47][38352][0]軸を下げたところに取る $x$軸を下げたところに取る

図8における直線$y=-2$を新たに$x$軸とし, 図9のように点をとって非交差経路を対応させると, これらは$\Omega_{n+1}$そのものであることがわかる.

$i$行$j$列目の成分が$r_{i+j-1}$である行列
\begin{pmatrix} r_{1} & r_{2} & \dots & r_{n} \\ r_{2} & r_{3} & \dots & r_{n+1} \\ \vdots & \vdots & \ddots & \vdots \\ r_{n} & r_{n+1} & \dots & r_{2n-1} \end{pmatrix}
を$H_n$, $i$行$j$列目の成分が$s_{i+j-1}$である行列
\begin{pmatrix} s_{1} & s_{2} & \dots & s_{n} \\ s_{2} & s_{3} & \dots & s_{n+1} \\ \vdots & \vdots & \ddots & \vdots \\ s_{n} & s_{n+1} & \dots & s_{2n-1} \end{pmatrix}
を$G_n$とすると,
$$|\Pi_n|=\mathrm{det}(H_n), |\Omega_n|=\mathrm{det}(G_n)$$

LGV公式より従う. LGV公式についてはこちらを参照.

$r_n=2s_n$

$(0,0)$から$(2n,0)$へ向かう経路であって(i)(ii)の条件を満たすもののうち、(iii)をみたすものの個数と(iii)をみたさないものの個数が等しいことを示せばよい. これらの集合の間に次のように全単射を構成する:
(iii)をみたさない経路について, 左から見たときに最後に登場する$(x,y)=(2,0)$の移動を$\longrightarrow$で表し, その左側の経路を$P$, 右側の経路を$Q$とする. 与えられた経路$"P\longrightarrow Q"$を$"\nearrow P\searrow Q"$に対応させる写像を考えると, これは全単射である($\nearrow, \searrow$でそれぞれ$(x,y)=(1,1),(1,-1)$の移動を表す). これは, (iii)をみたす経路について, 左から見たときに(始点を除いて)はじめて$x$軸上に点がのるまでの経路を$"\nearrow P \searrow"$とみなして先ほどと逆の操作を行うことを考えれば分かる.

経路!FORMULA[75][1342216998][0] 経路$"P\longrightarrow Q"$
経路!FORMULA[76][-204315566][0] 経路$"\nearrow P\searrow Q"$
図では$P$を赤色で, $Q$を青色で, 矢印部分を緑色で表している.

以上より$|\Pi_n|$を求める準備が整いました！

$|\Pi_n|$を求める

補題2と補題3より, $I_n$を単位行列とすれば
$$|\Pi_n|=\det(H_n)=\det(2I_nG_n)=\det(2I_n)\det(G_n)=2^n|\Omega_n|$$
が従うので, 補題1とあわせて
$$|\Pi_{n+1}|=2^{n+1}|\Omega_{n+1}|=2^{n+1}|\Pi_n|$$
より$|\Pi_n|$の漸化式が得られました！あとは$|\Pi_1|=2^1$とあわせて,
$$|\Pi_n|=2^{\frac{n(n+1)}{2}}$$
が分かります.