コンパクトハウスドルフ空間の連結成分について
初めに
この記事の内容コンパクトハウスドルフ空間の連結成分は、その連結成分を含む「開かつ閉集合」全体の共通部分である、という命題について書きます。この命題についてはイメージが湧いていませんが、ひとまず記事を書いてみることにしました。
証明の流れ
簡単に証明の流れを書きます。詳細については 本題 で述べます。$K$ を連結成分、$L$ を $K$ を含む開かつ閉集合全体の共通部分とします。
★ 目標：$L$ が連結であることを示すことstep1. $L$ が連結でないと仮定
step2. $L$ を分割する閉集合を取ることができる
step3. step2 の閉集合を分離する開集合を取ることができる
step4. step3 の開集合を使って、$K$ を含むが $L$ を含まない開かつ閉集合 $W$ を構成する←矛盾が生じた
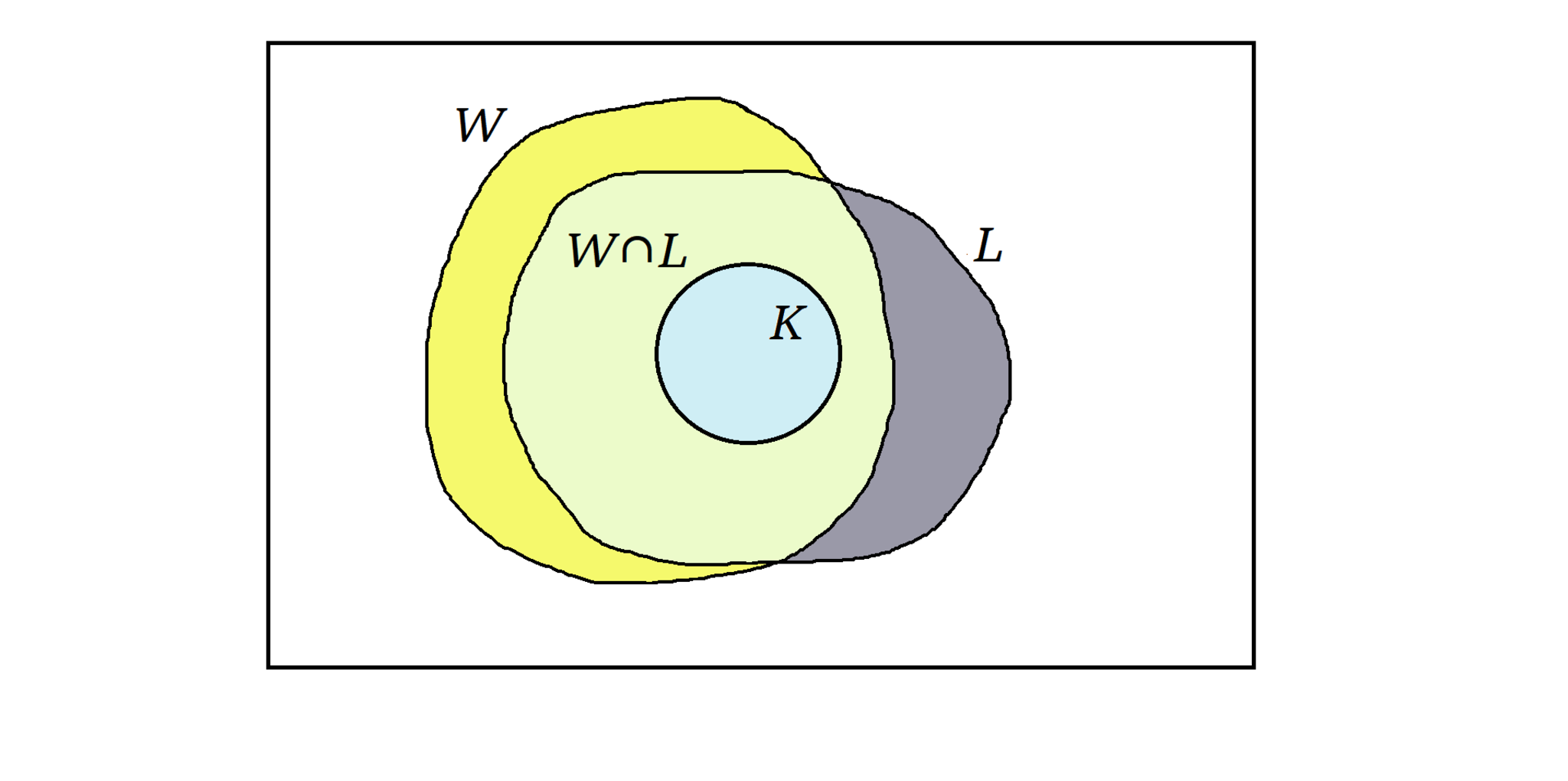証明の流れ step4
準備
まず、コンパクトと有限交叉性について整理します。以下は 【Mathpedia】定義 9.11 (有限交叉的な集合族) を参考にさせていただきました。
位相空間 $X$ の部分集合族 $\mathcal{A}$ が有限交叉性をもつとは、次が成り立つことをいう：
次の補題は 【Mathpedia】命題 9.12 (コンパクト性と有限交叉的な閉集合族) を参考にさせていただきました。
$X$ を位相空間、$\mathcal{F}_X$ を $X$ の閉集合全体とする。次は同値である：
(1) $X$ はコンパクトである。
(2) 有限交叉性をもつような任意の $\mathcal{A} \subset \mathcal{F}_X$ に対して、$\displaystyle \bigcap_{A\in \mathcal{A}} A \neq \emptyset$ である。
次の補題は、参考文献[1]の p.81 H) を参考にさせていただきました。
$X$ をコンパクト位相空間、$\mathcal{F}_X$ を $X$ の閉集合全体、$\mathcal{A} \subset \mathcal{F}_X $ とする。このとき, $\displaystyle \bigcap_{A \in \mathcal{A}} A$ を含む任意の開集合 $O$ に対して, $\displaystyle\bigcap_{i = 1}^n A_i \subset O$ を満たすような $A_1,\ \cdots,\ A_n \in \mathcal{A}$ が存在する。
$\mathcal{A}' := \lbrace \ O^c \cap A \ | \ A \in \mathcal{A} \ \rbrace \subset \mathcal{F}_X$ とおくと、$\displaystyle\bigcap_{A' \in \mathcal{A}'} A' = \displaystyle\bigcap_{A \in \mathcal{A}} (O^c \cap A) = O^c \cap F = \emptyset$ であるから、補題 1 により $\mathcal{A}'$ は有限交叉性をもたない. よってある $A_1,\ \cdots,\ A_n \in \mathcal{A}$ が存在して, $\displaystyle\bigcap_{i = 1}^n (O^c \cap A_i) = \emptyset$ となる。すなわち $\displaystyle\bigcap_{i = 1}^n A_i \subset O$ である。
本題
以下は 【数学についてのwebノート】位相空間における連結性の定義 の「定義：連結位相空間」の(定義1)、「定義：連結部分集合･連結部分空間」の(定義2)を参考にさせていただきました。
$X$ を位相空間、$Y$ を $X$ の部分空間とする。
$(1)$ $X$ が連結であるとは、次を満たす $X$ の開集合 $U_1,\ U_2$ が存在しないことをいう：
$$ X = U_1 \cup U_2,\ U_1 \neq \emptyset,\ U_2 \neq \emptyset,\ \ U_1 \cap U_2 = \emptyset$$
$(2)$ $Y$ が連結であるとは、次を満たす $X$ の開集合 $U_1,\ U_2$ が存在しないことをいう：
$$ Y \subset U_1 \cup U_2,\ U_1 \cap Y \neq \emptyset,\ U_2 \cap Y \neq \emptyset,\ U_1 \cap U_2 \cap Y = \emptyset$$
以下が本記事のメインとなる命題です。参考文献[1]の p.95 F) を参考にさせていただきました。
$X$ をコンパクトハウスドルフ空間、$K$ を $X$ の連結成分、$\mathcal{O}_X$ を $X$ の開集合全体、$\mathcal{F}_X$ を $X$ の閉集合全体とする。このとき、
$$ K = \displaystyle \bigcap_{K\subset A,\ A \in \mathcal{O}_X \cap \mathcal{F}_X}A$$
が成り立つ。
$\mathcal{A} := \lbrace \ A \in \mathcal{O}_X \cap \mathcal{F}_X \ |\ K\subset A \ \rbrace,\ L := \displaystyle \bigcap_{A \in \mathcal{A}} A$ とおく。$L$ が連結ならば、$K = L$ となる。そこで $L$ が連結でないと仮定すると、次を満たす $U_1,\ U_2\in \mathcal{F}_X$ が存在する：
$$ L \subset U_1 \cup U_2,\ L\cap U_1 \neq \emptyset,\ L\cap U_2 \neq \emptyset,\ L\cap U_1 \cap U_2 = \emptyset \cdots (*)$$
$K$ は連結であるから、$K \subset U_1$ としてよい。$L\cap U_1 ,\ L\cap U_2 \in \mathcal{F}_X$ であり、$X$ は正規空間であるから、次を満たす $V_1,\ V_2\in \mathcal{O}_X$ が存在する：
$$ L\cap U_1 \subset V_1,\ L\cap U_2 \subset V_2,\ V_1 \cap V_2 = \emptyset \cdots (**)$$
補題 2 より、$\displaystyle \bigcap_{i=1}^n A_i \subset V_1 \cup V_2$ を満たす $A_1,\ \cdots,\ A_n \in \mathcal{A}$ が存在する。$M := \displaystyle \bigcap_{i=1}^n A_i$ とおくと
$$ L \subset M \subset V_1 \cup V_2,\ M \in \mathcal{O}_X \cap \mathcal{F}_X$$
である。$W_1 := M\cap V_1,\ W_2 := M\cap V_2$ とおくと、$W_1,\ W_2 \in \mathcal{O}_X$ である。また、
$$ W_1 \cup W_2 = M,\ W_1\cap W_2 = \emptyset$$
であるから $W_1,\ W_2 \in \mathcal{O}_X \cap \mathcal{F}_X$ である。さらに $K\subset L\cap U_1 \subset M \cap V_1 = W_1$ より、$ W_1 \in \mathcal{A}$ であるから $L \subset W_1$ である。しかし、$(*)$、$(**)$ より $L \not \subset V_1$ であるから $L\not \subset W_1$ である。これは矛盾である。したがって $L$ は連結である。
