釣り糸の長さについて

研究の動機

一様重力場で物体をいくらかの仰角を以て投射すると、その物体の軌道は放物線となる。これは古典力学の中でもよく知られている現象である。
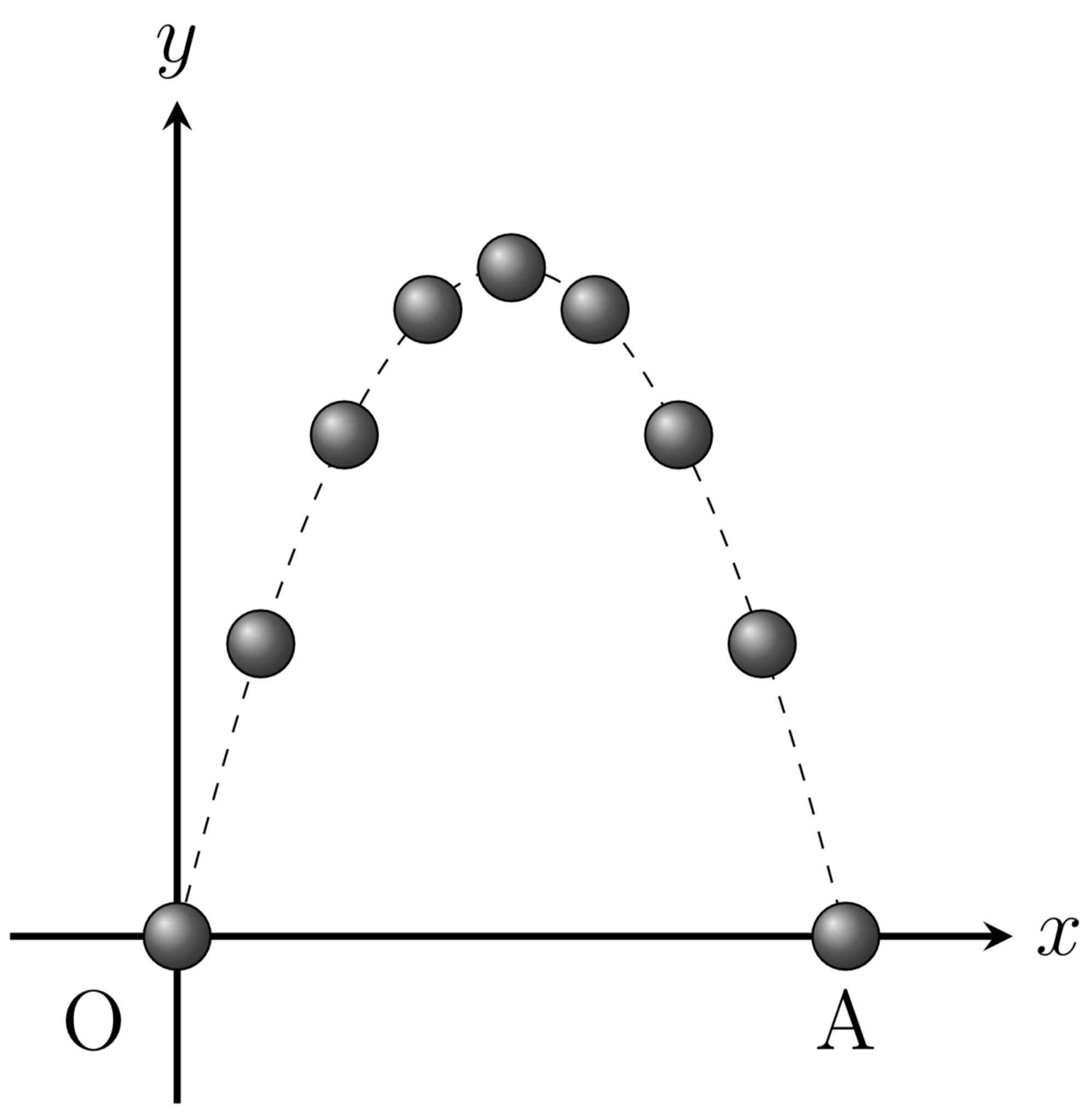物体を斜方投射した時の様子

とある映画で、ペットボトルで作ったロケットに釣り糸をつないで飛ばすシーンがあった。釣り糸は回転計の備わったリール付きの釣り竿につながっており、回収を容易にするだけでなく、釣り糸がどのくらい引き出されたか、その長さが分かる仕組みになっていた。

これを見て、どのくらいの長さの釣り糸を用意すれば、釣り糸に邪魔されることなくこの実験を行うことができるのかが気になった。

今回はこの疑問を、初等的な微積分を用いて解明することにした。

目標

この記事では以下を目標に議論を進める。

準備

以下では、議論で用いる力学と数学の設定、公式等を列挙する。

力学

設定

1. 物体の投射位置を原点$\mathrm{O}$とし、$x$軸と$y$軸をそれぞれ図のように設ける。
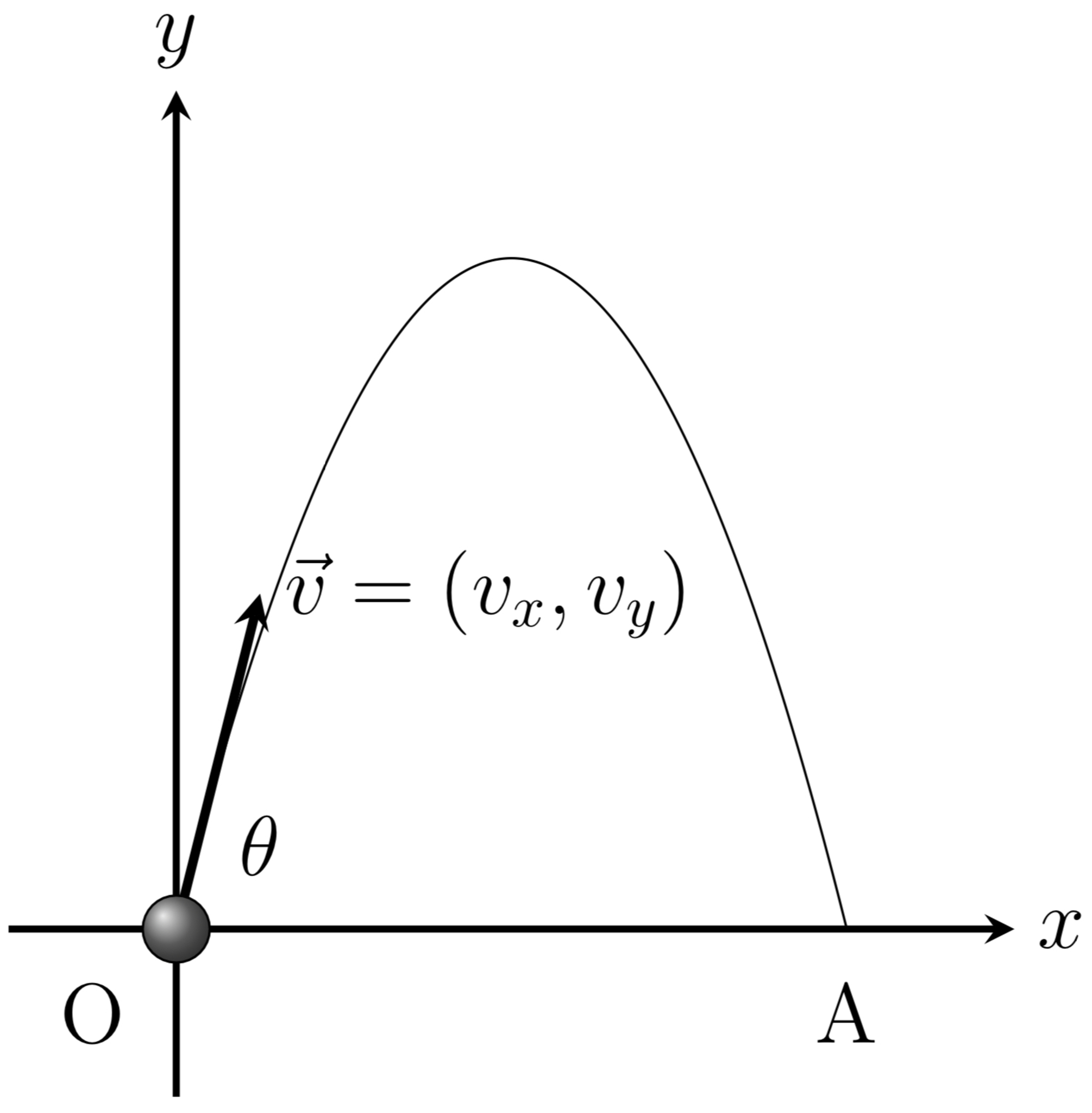   座標軸の設定
2. 物体は仰角$\theta$で投射する。ただし、$0<\theta<\cfrac{\pi}{2}$とする。
3. 物体は$xy$平面内を運動し、$x$軸上の点$\mathrm{A}$に落下する。
4. 重力加速度と初速度はベクトル量でそれぞれ$\vec{g}=(0,-g)$、$\vec{v_0}=(v_{0x},v_{0y})$である。ただし、$g,v_{0x},v_{0y}$は正の数である。
5. 重力加速度の大きさ$g$と、投射初速度の大きさ$v_0$は一定である。
6. 物体は質量$1$の質点とみなす。すなわち回転などは考えない。
7. 空気抵抗や電磁気的な作用などは無視する。つまり、物体に働く力は重力$1\vec{g}=\vec{g}$だけである。
8. 単位は国際単位系SIに従う。
9. 糸は軽く丈夫で伸縮しない。

公式

1. 時刻$0$で初速度$\vec{v_0}=(v_{0x},v_{0y})$で投射した物体の、時刻$t$における速度$\vec{v}$は$\vec{v}=(v_{0x},v_{0y}-gt)$

2. 時刻$0$で初速度$\vec{v_0}=(v_{0x},v_{0y})$で投射した物体の、時刻$t$における変位$\vec{r}$は$\vec{r}=\left(v_{0x}t,v_{0y}t-\cfrac{gt^2}{2} \right)$

3. 仰角$\theta$で投射する場合の初速度ベクトルの成分$\vec{v_0}=(v_{0}\cos{\theta},v_{0}\sin{\theta})$

数学

公式

1. $a\leqq x\leqq b$で定義された$C^1$曲線$y=f(x)$の$x=a$から$x=b$までの道のり$s$は$$ s=\int_{a}^{b} \sqrt{1+\{f^\prime(x)\} ^2}\mathrm{d}x$$

2. 積分定数を省略する。実数$\alpha$に対して不定積分$$\int \sqrt{x^2+{\alpha}^2}\mathrm{d}x=\cfrac{1}{2}\left\{x\sqrt{x^2+{\alpha}^2}+ {\alpha}^2\log{\left(x+\sqrt{x^2+ {\alpha}^2} \right)} \right\}$$

議論と導出

軌道の表式

まず、$xy$平面上での軌跡を確認するために、変位を$x,y$で表す。
力学公式より、$$\begin{cases} v_x=v_0\cos{\theta}\\ v_y=v_0\sin{\theta}-gt \end{cases} \tag{1}$$
ゆえに、
$$\begin{cases} x=v_0\cos{\theta}\ t\\ y=v_0\sin{\theta}\ t-\cfrac{1}{2}gt^2 \end{cases} \tag{2}$$
これより、$t=\cfrac{x}{v_0\cos{\theta}}$を$y$の式に代入して整理すると
$$y=-\cfrac{g}{2v_0^2\cos^2 {\theta}}x^2+\tan{\theta}\ x \tag{3}$$
を得る。

ここで、$\mathrm{A}$の$x$座標は、$x\ne 0$の下で$y=0$となる$x$であるから、軌道の式で$y=0$として$x$について解けば$$\mathrm{A}(\cfrac{v^2\sin{2\theta}}{g},0) \tag{4}$$を得る。

よって、軌道の式は$\mathrm{A} $の座標を用いて、
$$y=-\cfrac{gx}{2v_0^2\cos^2 {\theta}}\left(x-\cfrac{v^2\sin{2\theta}}{g} \right) \tag{5}$$

とも書き換えられる。

放物線の長さ

$a,p$を$0$でない正数とする。
放物線$C:y=-ax(x-p)$　$(y\geqq 0)$の長さ$s$を求めてみよう。
$C$を展開して微分すると以下のようになる。
$y=-ax(x-p)$
$y=-ax^2+apx$
$y^\prime =-2ax+ap$

よって、数学公式1より、
$$s=\int_{0}^{p}\sqrt{1+(-2ax+ap)^2}\mathrm{d}x $$
これを整理する。展開して平方完成すると次のようになる。
$$s=\int_{0}^{p}\sqrt{1+\left\{2a\left(x-\frac{p}{2}\right)\right\}^2 }\mathrm{d}x $$

ここで、$t=2a\left(x-\cfrac{p}{2}\right)$と変数変換する。
$\mathrm{d}t=2a\mathrm{d}x$より、$\mathrm{d}x=\cfrac{\mathrm{d}t}{a} $

ここで、放物線は軸対称なので、$s$の式は次のように書き換えて良い。
$$s=2\int_{p/2}^{p}\sqrt{1+\left\{2a\left(x-\frac{p}{2}\right)\right\}^2 }\mathrm{d}x $$
これを$t$の式で書き換える。
$$s=\cfrac{1}{a}\int_{0}^{ap}\sqrt{1+t^2 }\mathrm{d}t $$

よって、数学公式2において、公式の${\alpha}$を${\alpha}=1$とすれば
$$s=\cfrac{1}{2a}\left[t\sqrt{t^2+1}+\log{\left(t+\sqrt{t^2+1} \right)} \right]^{ap}_{0}$$
$$s=\cfrac{1}{2a}\left[ap\sqrt{(ap)^2+1}+\log\left\{ap+\sqrt{(ap)^2+1}\right\}\right] $$
これが、この$C$の長さである。

釣り糸の長さ

前項の結果を用いる。
軌道の方程式$$y=-\cfrac{g}{2v_0^2\cos^2 {\theta}}x^2+\tan{\theta}\ x$$
と前項で出てきた$C$の方程式
$$y=-ax^2+apx$$
を比較すれば、$a=\cfrac{g}{2v_0^2\cos^2 {\theta}}$、$ap=\tan{\theta}$なので、これを$s$の式に代入すると

$$s=\cfrac{v_0^2\cos^2 {\theta}}{g}\left\{\tan{\theta}\sqrt{1+\tan^2{\theta}}+\log{\left(\tan{\theta}+\sqrt{1+\tan^2{\theta} } \right) } \right\} $$

$1+\tan^2{\theta}=\cfrac{1}{\cos^2{\theta}}$を用いて、これを$\tan{\theta}$だけで表す。この$s$が、仰角$\theta$における釣り糸の長さの最小値である。たしかにこれは$g,v_0$一定の下では仰角だけで表されている。

具体的な計算

斜方投射においては、仰角$\theta=\cfrac{\pi}{4}$で最も遠くへ投げることが出来る。
これは、力学でもよく知られた事実であるし、前項の点$\mathrm{A}$の$x$座標$\cfrac{v^2\sin{2\theta}}{g}$が$\theta=\cfrac{\pi}{4}$で最大値をとることからもわかる。

では、このときの釣り糸が最低いくらあれば良いだろうか。

前述の公式1を利用する。これに$\theta=\cfrac{\pi}{4}$を代入すれば

$$s=\cfrac{v_0^2(\sqrt{2}+\log{(1+\sqrt{2})})}{2g}$$

$g=9.8$m/s${}^2$、$v=20$m/sとすれば、物体の落下地点$\mathrm{A} $は原点からおよそ$40.8$m離れていて、釣り糸は最低でも$s\fallingdotseq 46.8$m必要であることが計算によって分かる。

感想と今後の課題

式の形は複雑に見えるが、初等的な微積分が力学でどのように応用されるのかの一例が垣間見えて実に面白かった。

さらに面白いことに、釣り糸の長さを最大とする仰角$\theta $は$\theta=\cfrac{\pi}{4}$ではなかった。これは、上記の具体的な計算において$s$と$\theta$の関係を調べるためにdesmosを走らせた時に判明したものである。

青線が物体の実際の軌道、赤線が$s-\theta$の関係をあらわすグラフ

この赤いグラフに注目すると、$s$の最大値を与える$\theta$は$\cfrac{\pi}{4}$より大きいことが分かる。
では、$g,v_0$一定の下で釣り糸の長さを最大とする仰角$\theta$はいくらなのだろうか。定理1を$\theta$で微分すれば分かりそうだが煩雑そうで戦慄する。
いつか計算してみたい。