完備ブール代数の商ブール代数は必ず完備？

この記事では、ブール代数とそのイデアルによる商、完備性の知識を仮定する。

次の問題を考えよう。

自分で考えたい人はここで一旦読むのをやめて考えてみてください。

太郎と花子と対話が始まります。

太郎

先生から上のような問題をもらったよ。
でも今回の問題はかんたんだよね。
$B$に入っている無限meetと無限joinをそのまま$B/I$の演算に落とせばいいじゃん。

花子

あらそうかしら。
それって、$B/I$の元たち$([b_i] : i \in A)$のjoinをたとえば、
$$ \bigvee_{i \in A} [b_i] = \left[\bigvee_{i \in A} b_i\right] $$
と定義するということよね。これはwell-definedかしら？

太郎

あっ、たしかに…。

花子

うん、これはwell-definedでないことを示せるわね。
自然数全体の集合$\omega$の冪集合のブール代数$B = \Pow(\omega)$を考えよう。これは完備ブール代数ね。
$\omega$の有限部分集合のなすイデアルを$\fin$と書くことにしよう。
ブール代数$\Pow(\omega)/\fin$にさっきのようにwell-definedにjoinは定まらないわね。

実際、1点集合たち$\{n\}$ ($n \in \omega$)は$\Pow(\omega)/\fin$ではそれぞれ$0$に潰れるけど、その和集合は$\omega$、つまりブール代数の$1$になる。もし上の演算がwell-definedだったら$\Pow(\omega)/\fin$で$0 = 1$となりそれは矛盾だわ。

太郎

分かった。花子さんのさっきの証明から問題は偽なんだ！
つまり、$\Pow(\omega)$と$\Pow(\omega)/\fin$が反例！

花子

うーん、それはまた先走り過ぎかしら。
上で太郎くんが考えてくれた演算の定義がうまくいかなかっただけで、本当はもっとうまい無限個のjoinとmeetを定義できる可能性、というのを排除していないからね。

太郎

そうか、どう示せばいいんだろう？花子さん、教えて。

花子

わかりやすさのために$\Pow(\omega)$と$\Pow(\omega \times \omega)$を同一視しよう。
すると考えるべき図形は平面になるね。
$A_n = [n, \omega) \times \omega$
という集合を考えよう。

太郎

ははあ、$[n, \omega)$は$n$以上の自然数がなす集合という意味で、こんな感じだね。
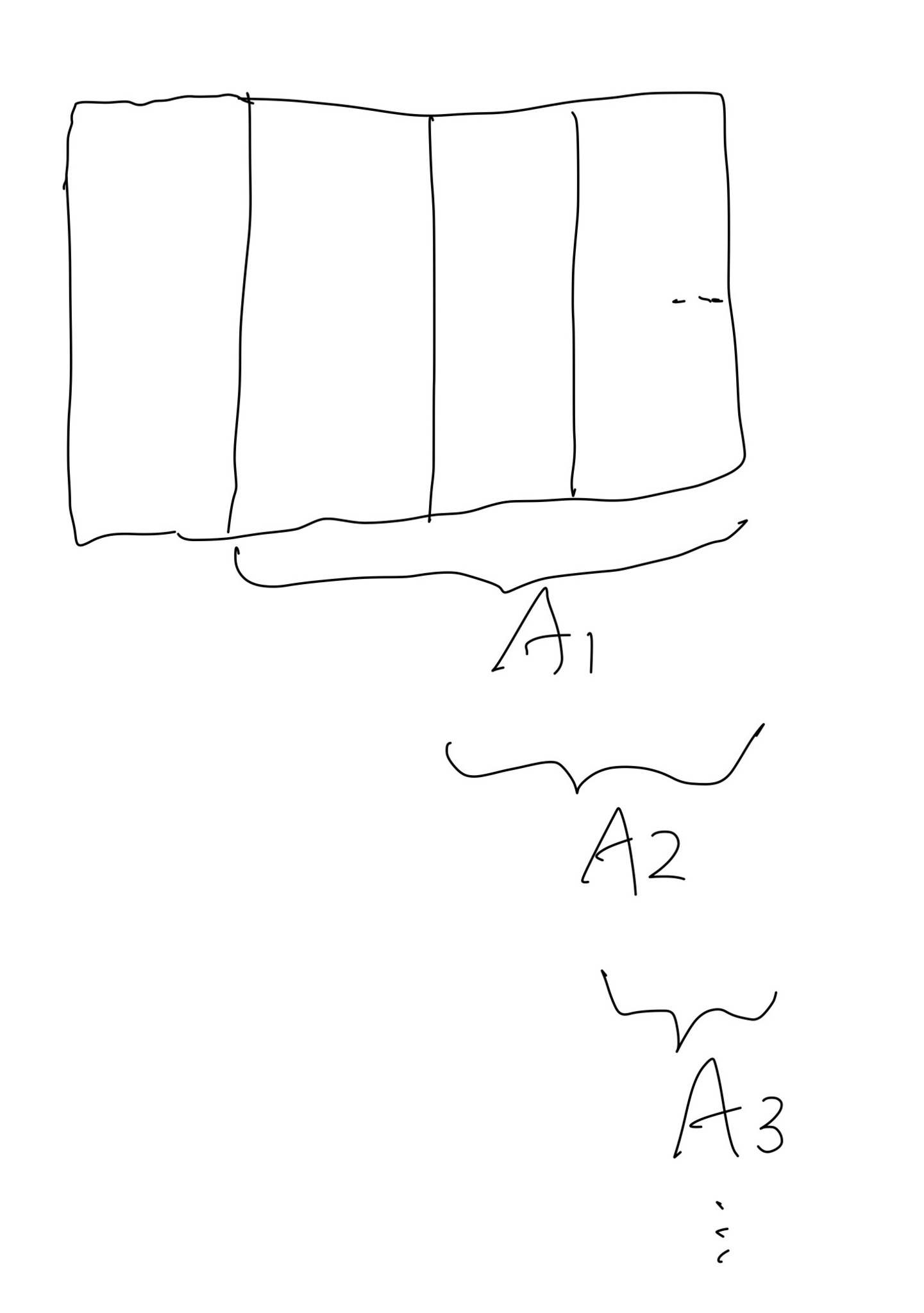平面

花子

その通り。もちろん、これらの集合を$\Pow(\omega\times\omega)$で考えたら、下限が存在し、それは$0$だ。ところが$\Pow(\omega\times\omega)/\fin$で考えたらどうなるかしら？

太郎

むむ。まさか、$0$以外の下界が存在する？

花子

そう。たとえば、$B = \omega \times \{0\}$を考えよう。

太郎

図はこんな感じか。
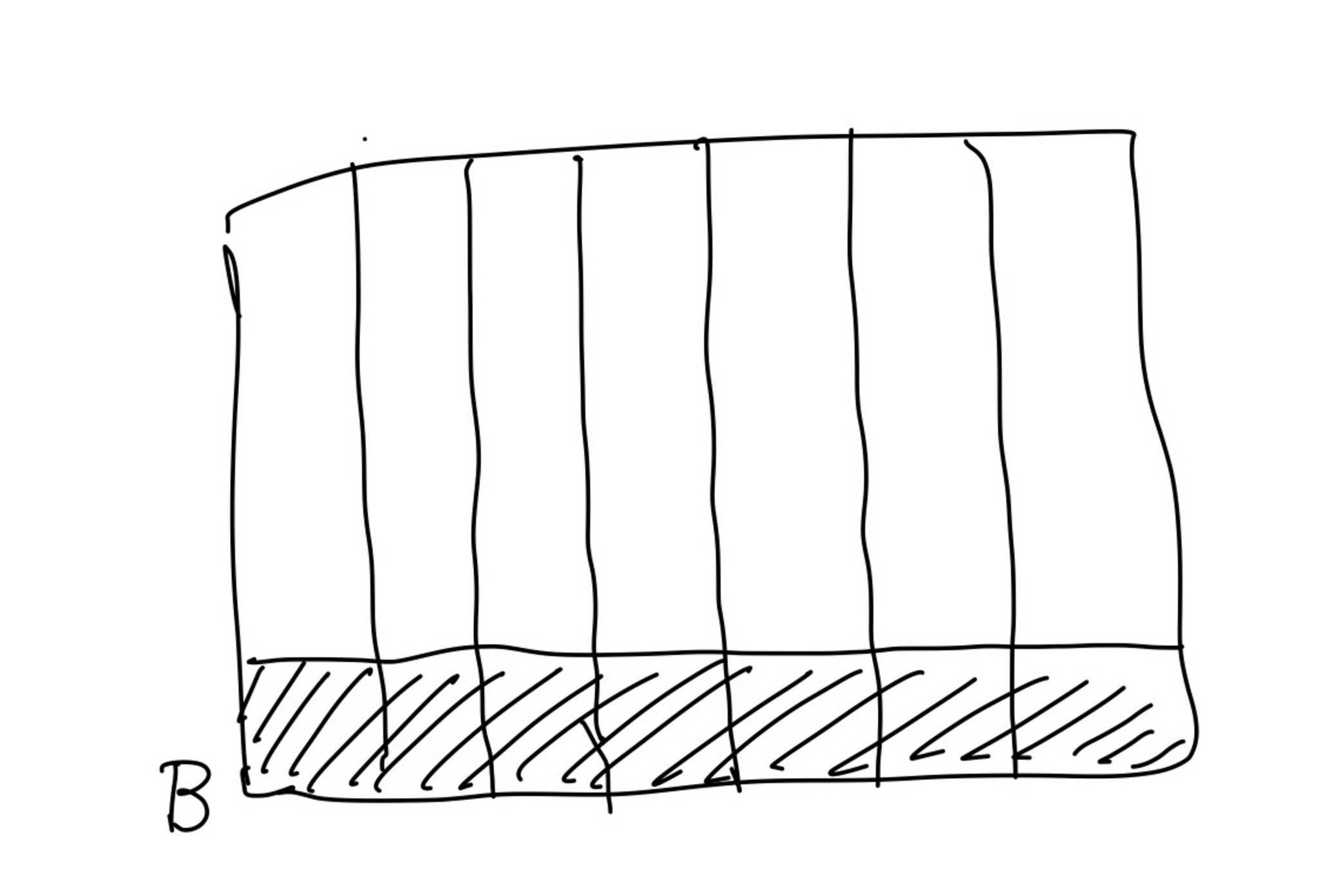Bを加えた図
あっ、そうか。
$\Pow(\omega\times\omega)/\fin$の世界では$B$も$A_n$たちの下界だ。
実際、$B \setminus A_n$は有限集合しか残らないから$[B]_{\fin} \le [A_n]_{\fin}$が成り立つ！

太郎

しかも縦幅を各カラムの中で有限の範囲なら好きに大きくできるだから、いくらでも大きい下界が構成できる！
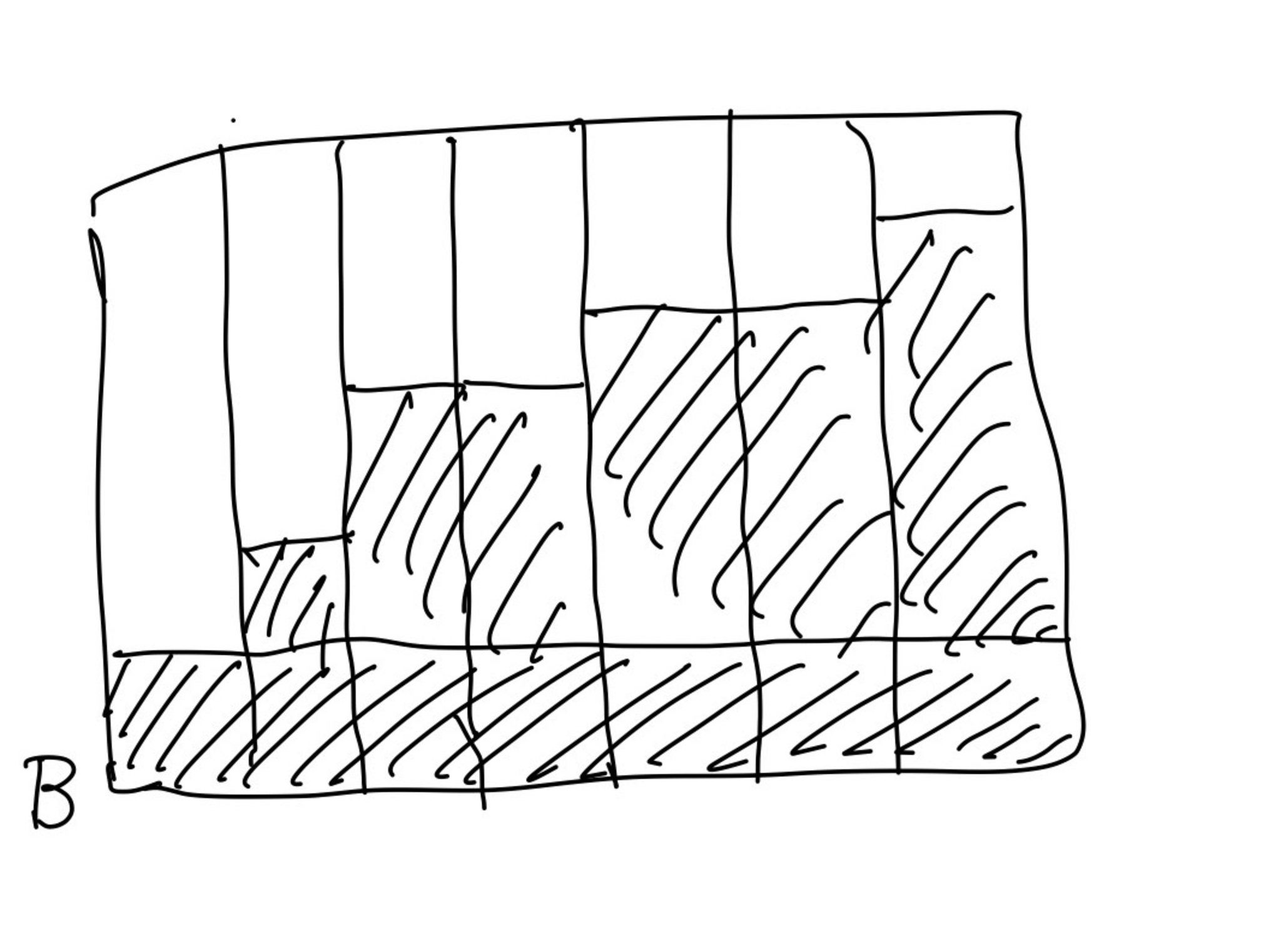もっと大きいB
というわけで、$[A_n]_\fin$たちの最大下界はないのか！つまり$\Pow(\omega\times\omega)/\fin$は完備でない！

花子

そう、そうでいい。本当は任意の下界がその図のような形に含まれることを示さないといけないけど、それはまあかんたん。

太郎

うーん、また花子さんの力に頼り切りだったなあ。
あれ、この問題カード、裏にもなにか書いてある。

花子

なるほど…。これは私宛ての問題ってところか。

続く (いいえ)

某ガールの設定パクリですね。すいません。