大学数学基礎解説

文献あり

グラフ理論の基本

グラフ理論

1122

この記事は、ほかの記事でグラフ理論を使うときの説明用の記事です。ほかの記事で必要な内容が出るたびに更新する予定です。

記号について

集合や写像についての基礎的な知識は前提とし用語や記号は断りなく使います。

集合 $S$ に対して、 $[S]^{n}$ で $S$ の $n$ 元からなる部分集合全体を表します。形式的に書けば $[S]^{n} = {X \subset S ∣ | X | = n}$ となります。

無向グラフ

グラフとは

単純グラフ

グラフとは図1のように頂点と辺からなる図形です。グラフを考える際には、頂点の位置や辺の長さ・形は意味を持たず、頂点と辺の接続関係だけに注目します。身近な例としては、路線図を考えるとわかりやすいでしょう。路線図はどの駅にどの路線が通っているかが重要で、その形が実際の線路の形そっくりになっている必要はありません。駅の位置関係も、実際とは異なっていても構いません。

グラフの例

グラフの形式的な定義は以下のようになります。

単純グラフ

頂点集合 $V$ 、辺集合 $E \subseteq [V]^{2}$ の組 $G = (V, E)$ を単純グラフといいます。

図1のグラフは頂点集合 $V = {v_{1}, v_{2}, v_{3}, v_{4}, v_{5}, v_{6}, v_{7}, v_{8}}$ 、辺集合 $E = {{v_{1}, v_{2}}, {v_{2}, v_{3}}, {v_{3}, v_{1}}, {v_{4}, v_{5}}, {v_{4}, v_{6}}, {v_{4}, v_{7}}}$ のグラフ $G = (V, E)$ です。

ハイパーグラフ

先に路線図の例を挙げました。駅を頂点、路線を辺とすると一つの辺に3つ以上の頂点が接続していることになります。このように、辺の要素数の制限をなくしたものをハイパーグラフといいます。

ハイパーグラフ

頂点集合 $V$ 、辺集合 $E \subseteq P (V)$ の組 $G = (V, E)$ をハイパーグラフといいます。

単純グラフはハイパーグラフの特別な場合と言えます。

多重グラフ

図2のような図形もまたグラフと呼ばれます。 $e_{2}$ のような両端点ともひとつの頂点であるような辺をループといい、 $e_{5}$ と $e_{6}$ のように両端点ともを共有する辺を多重辺といいます。多重辺やループを持つグラフを多重グラフといいます。逆に単純グラフとは多重辺やループを持たないグラフです。

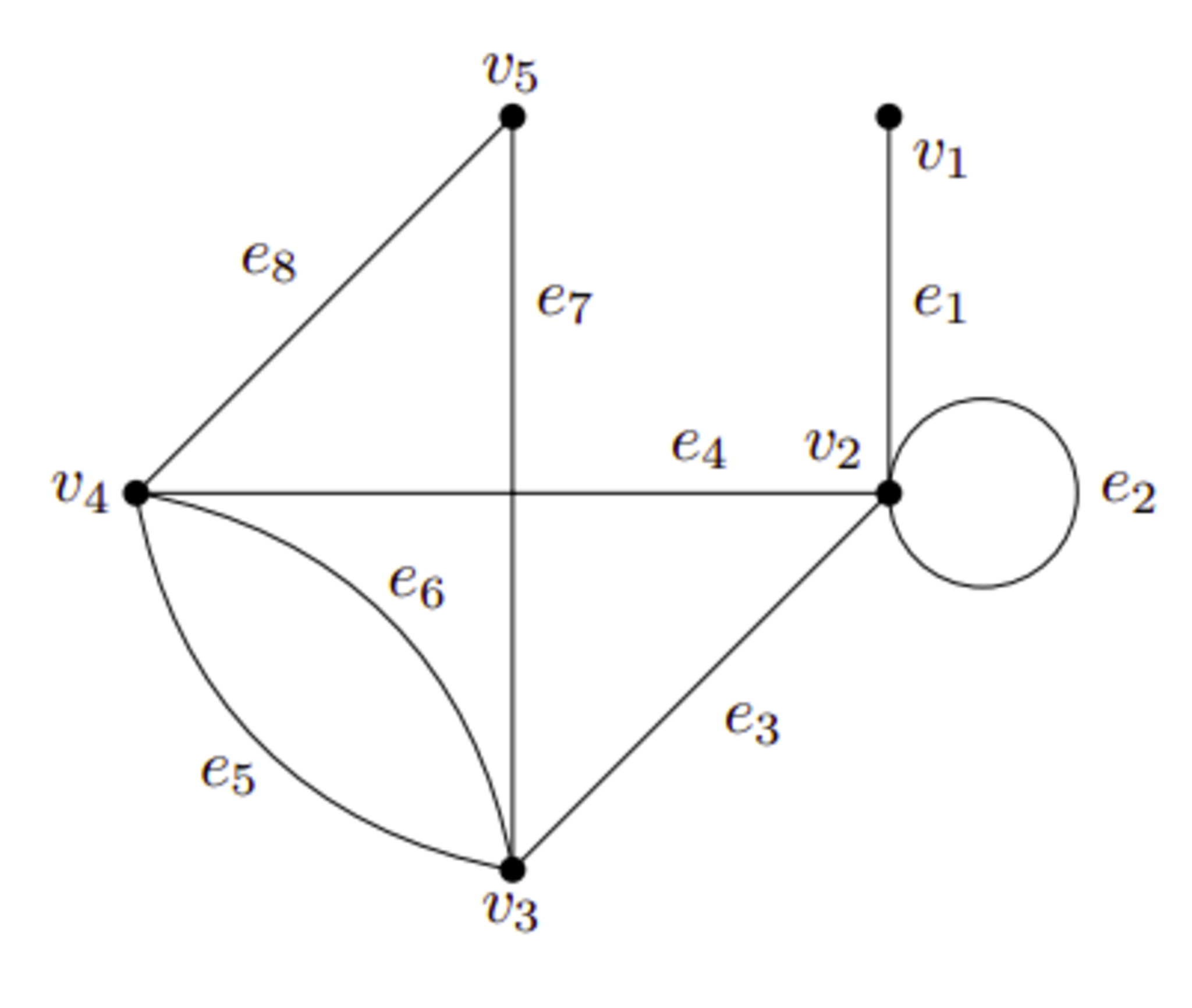多重グラフの例

多重グラフの形式定義は以下の通りです。

多重グラフ

頂点集合 $V$ 、辺集合 $E$ 、接続関数 $ψ : E \to [V]^{1} \cup [V]^{2}$ の組 $G = (V, E, ψ)$ を多重グラフといいます。

図2では、 $V = {v_{1}, v_{2}, v_{3}, v_{4}, v_{5}}$ 、 $E = {e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{7}, e_{8}}$ であり、接続関数 $ψ$ は $\begin{aligned} ψ (e_{1}) & = {v_{1}, v_{2}} \\ ψ (e_{2}) & = {v_{2}} \\ ψ (e_{3}) & = {v_{2}, v_{3}} \\ ψ (e_{4}) & = {v_{2}, v_{4}} \\ ψ (e_{5}) & = {v_{3}, v_{4}} \\ ψ (e_{6}) & = {v_{3}, v_{4}} \\ ψ (e_{7}) & = {v_{3}, v_{5}} \\ ψ (e_{8}) & = {v_{4}, v_{5}} \end{aligned}$
となっています。

単純グラフはループや多重辺を持たない多重グラフだと考えることができます。単純グラフで考えるより多重グラフで考えたほうが自然で、証明などもしやすくなるような場合もあります。

（ところでハイパーグラフで多重グラフなグラフって聞かない気がします。定義すること自体は簡単ですが、何かそういうグラフが使われている例とかってあるんでしょうか。ご存じの方がいらっしゃいましたらコメントなどで教えてください。）

基本的な用語

グラフ $G$ の頂点集合を $V (G)$ 、辺集合を $E (G)$ 、接続関数を $ψ (G)$ と書きます。例えばグラフ $H = (W, F)$ に対して $V (H) = W$ 、 $E (H) = F$ です。 $W (H)$ とは書きません。グラフと頂点集合・辺集合を厳密に区別せず、例えば $v_{1} \in G$ 、 ${v_{2}, v_{4}} \notin G$ のように書いたりもします。

グラフ ${\emptyset, \emptyset}$ を空グラフと呼びます。

接続・隣接

頂点 $v$ と辺 $e$ に対して、 $v \in e$ （多重グラフなら $v \in ψ (e)$ ）となるとき、 $v$ は $e$ に接続するといい、 $e$ を $v$ の接続辺といいます。1つの辺に接続する2つの頂点はぞの辺の端点と呼び、辺はその端点を結ぶといいます。

辺 ${x, y}$ を単純に $x y$ （または $y x$ ）と書きます。多重グラフのときも $x$ 、 $y$ が $e$ の端点であることを表すために $e = x y$ と書きますが、もはや $e$ を一意に定めることはできません。この書き方は $ψ (e) = {x, y}$ を省略したものとみることもできます。

グラフ $G$ に辺 $x y$ が在るとき、 $x$ と $y$ は隣接するといい、互いにほかの隣接点であると呼びます。また、2つの辺 $e \neq f$ が共通の端点を持つとき隣接するといいます。

グラフ $G = (V, E)$ において、頂点 $v$ の $G$ における隣接点全体の集合を $N_{G} (v)$ または単に $N (v)$ と表します。一般に、頂点からなる集合 $U \subseteq V$ に対して、 $U$ に属する頂点の $V ∖ U$ の中にある隣接点全体の集合を $U$ の近傍といい、 $N_{G} (U)$ または $N (U)$ と表します。このように、誤解の恐れがないときは添え字の $G$ を省略することがあります。

$X$ と $Y$ を頂点からなる集合とします。 $x \in X$ 、 $y \in Y$ となるような辺 $e = x y$ を $X$ - $Y$ 辺と呼びます。 $X$ - $Y$ 辺全体の集合を $E (X, Y)$ と表します。 $E ({x}, Y)$ や $E (X, {y})$ を単に $E (x, Y)$ や $E (X, y)$ と書きます。このように単元集合のとき、波括弧 ${}$ を省略することがあります。頂点 $v$ に接続する辺全体の集合を $E (v)$ と書きます。

次数

頂点 $v$ の次数 $d_{G} (v)$ とは $v$ に接続する辺の本数 $| E (v) |$ です。単純グラフなら、 $v$ の隣接点の個数に等しくなります。次数0に頂点を孤立点といいます。次数の最小値 $δ (G) := min {d (v) ∣ v \in V}$ を最小次数、最大値 $Δ (G) := max {d (v) ∣ v \in V}$ を最大次数と呼びます。

同型なグラフ

2つの単純グラフ $G = (V, E)$ 、 $G^{'} = (V^{'}, E^{'})$ について、一対一対応 $f : V \to V^{'}$ が存在して、全ての $x, y \in V$ に対して $x y \in E \Leftrightarrow f (x) f (y) i n E^{'}$ を満たすとき、 $G$ と $G^{'}$ は同型であるといい、 $G ≃ G^{'}$ と書き、この写像 $f$ を同型写像と呼びます。多重グラフのときは、同型写像が $f : V \to V^{'}$ と $g : E \to E^{'}$ の組 $(f, g)$ となり、条件が、全ての $x, y \in V$ 、 $e \in E$ に対して $ψ (e) = {x, y} \Leftrightarrow ψ^{'} (g (e)) = {f (x), f (y)}$ が成り立つことになります。

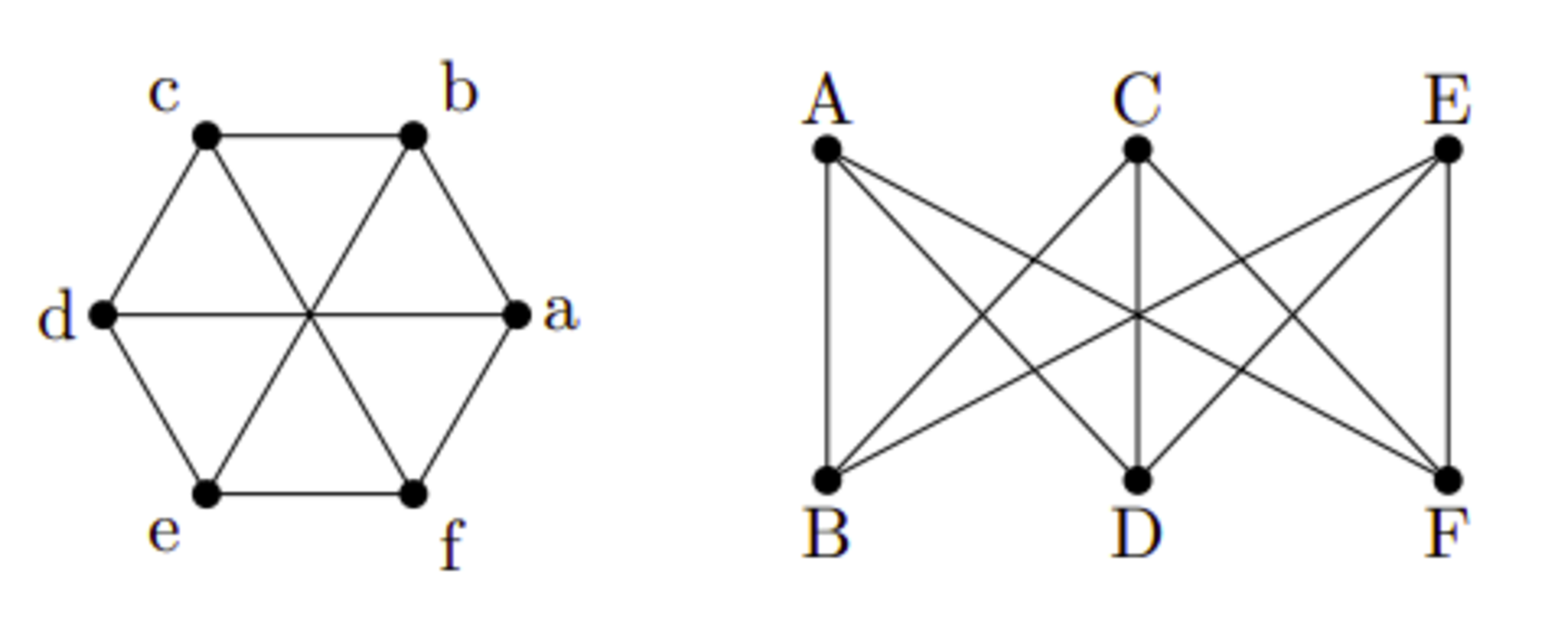同型なグラフ

部分グラフ

グラフ $G = (V, E)$ 、 $G^{'} = (V^{'}, E^{'})$ について、 $V^{'} \subset V$ 、 $E^{'} \subset E$ であり、頂点と辺の接続関係が保存されるとき、 $G^{'}$ を $G$ の部分グラフと呼び、 $G^{'} \subset G$ と書きます。

$G^{'} \subset G$ であり、 $G$ が $x, y \in V^{'}$ となるような辺 $x y \in E$ をすべて含むとき、 $G^{'}$ は $G$ の誘導部分グラフであるといいます。このとき、 $V^{'}$ は $G$ において $G^{'}$ を生成するといい、 $G^{'} = G [V^{'}]$ と書きます。

道

頂点と辺を交互に並べた空でない有限列 $W = v_{0} e_{1} v_{1} e_{2} \dots e_{k} v_{k}$ で各 $i \leq k$ に対し $e_{i} = v_{i - 1} v_{i}$ となるものを歩道と呼びます。また $v_{0}$ 、 $v_{k}$ を端点と呼び、特に $v_{0}$ を始点、 $v_{k}$ を終点と呼びます。

歩道 $W = v_{0} e_{1} v_{1} e_{2} \dots e_{k} v_{k}$ が相異なる $i, i^{'} \leq k$ に対し $e_{i} \neq e_{i^{'}}$ であるとき、これを小径と呼びます。さらに相異なる $j, j^{'} \leq k$ に対し $v_{j} \neq v_{j^{'}}$ であるとき、これを道と呼びます。

歩道（小径、道）の辺の本数をその長さと言います。始点と終点は本質的には違いがありませんが、これを決めておくことで歩道内の要素に順番が与えられるので便利なことがあります。小径は頂点の重複を許す道、歩道は辺の重複を許す道、というとらえ方もできます。

道の例

道はその頂点の集合 $V (P)$ と辺の集合 $E (P)$ からなる単純グラフ $P = (V (P), E (P))$ ととらえることもできます。道を表すために、その頂点だけを並べることも多いです。そのようなときは $P = v_{0} \dots v_{k}$ と書きます。

$0 \leq i \leq j \leq k$ とします。道 $P = v_{0} \dots v_{k}$ の一部を切り取ったものを以下のように表します。

$\begin{aligned} v_{i} P & = v_{i} \dots v_{k} \\ P v_{j} & = v_{0} \dots v_{j} \\ v_{i} P v_{j} & = v_{i} \dots v_{j} \\ \overset{˚}{P} & = v_{1} \dots v_{k - 1} \\ \overset{˚}{v_{i}} P & = v_{i + 1} \dots v_{k} \\ P \overset{˚}{v_{j}} & = v_{0} \dots v_{j - 1} \end{aligned}$

$P$ が長さ1の道であるとき、 $\overset{˚}{P}$ は空グラフになります。これはもはや道ではありません。

さらに、いくつかの道をつないで新たな道を作るとき、たとえば三本の道の和 $P x \cup x Q y \cup y R$ が道になるならば、これを単に $P x Q y R$ というように表します。

道 $P = v_{0} \dots v_{k}$ と頂点の集合 $A$ 、 $B$ について $V (P) \cap A = {v_{0}}$ かつ $V (P) \cap B = {v_{k}}$ となるとき、 $P$ を $A - B$ 道と言います。 $A$ - $B$ 道全体の集合を $P (A, B)$ で表します。以前と同様に波括弧を省略し $P (v_{0}, B)$ などと書いたりします。

連結

グラフ $G = (V, E, ψ)$ について、任意の $u, v \in V$ に対し $P (u, v) \neq \emptyset$ となるとき、 $G$ は連結であると言います。

直観的に言えばすべてつながっているグラフが連結なグラフです。

極大な連結部分グラフを連結成分と呼びます。

縮約

グラフのある辺を縮めて一つの頂点にすることを考えましょう。

図5のようにグラフ $G = (V, E)$ の辺 $e = x y \in E$ を選びます。この辺を新しい頂点 $v_{e}$ に置き換えます。このとき、 $x$ または $y$ と隣接していた頂点は $v_{e}$ と隣接するようにし、どちらとも隣接していない頂点は $v_{e}$ とも隣接しないようにします。

縮約

こうして得られたグラフを、 $G$ から、その辺 $e = x y$ を1つの頂点 $v_{e}$ に縮約して得られたグラフといい、 $G / e$ で表します。 $G / e$ の頂点集合と辺集合は、形式的には以下のように表されます。
$\begin{aligned} V (G / e) & = (V ∖ {x, y}) \cup {v_{e}} \\ E (G / e) & = {v w \in E ∣ {v, w} \cap {x, y} = \emptyset} \cup {v_{e} w ∣ x w \in E ∖ {e} または y w \in E ∖ {e}} \end{aligned}$

この縮約の操作を何度か繰り返し、 $G$ から新たにグラフ $X$ を作ることを考えるます。各 $x \in V (X)$ に対し、 $x$ に縮約された $G$ の頂点全体の集合を $V_{x}$ とすると、各 $V_{x}$ は連結であり、任意の $x, y \in V (X)$ に対し、 $G$ に $V_{x} - V_{y}$ 辺があることと、 $x y \in E (X)$ となることが同値です。集合 $V_{x}$ を $G$ の分岐集合と言います。

多重グラフの場合はもう少し単純です。両端点が共通な辺が許されるため、頂点集合、辺集合は以下のようになります。
$\begin{aligned} V (G / e) & = (V ∖ {x, y}) \cup {v_{e}} \\ E (G / e) & = E (G) ∖ {e} \end{aligned}$
そして、 $e$ 以外の $e^{'} \in E ∖ {e}$ に対して、 $ψ_{G / e} (e^{'})$ を新しい頂点集合に合わせて修正します。

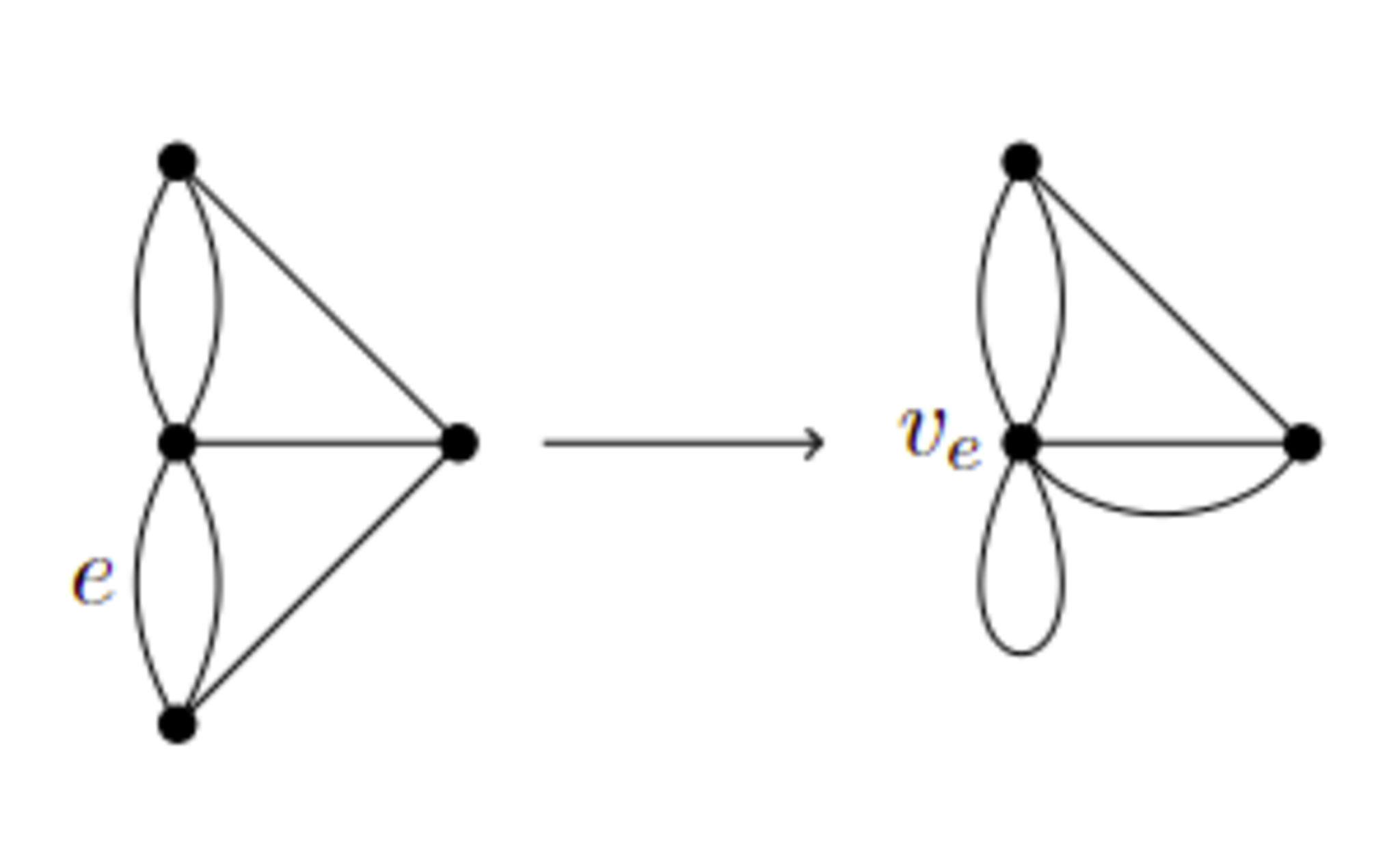多重グラフの縮約

有向グラフ

定義

有向単純グラフ

頂点集合 $V$ 、辺集合 $E \subset V^{2} ∖ {(v, v) ∣ v \in V}$ の組 $G = (V, E)$ を有向単純グラフと言います。

有向多重グラフ

頂点集合 $V$ 、辺集合 $E$ 、接続関数 $ψ : E \to V^{2}$ の組 $G = (V, E, ψ)$ を有向多重グラフと言います。

辺に向きを考えたものが有向グラフです。組は順序も考えるので、 $(u, v)$ と $(v, u)$ は異なります。

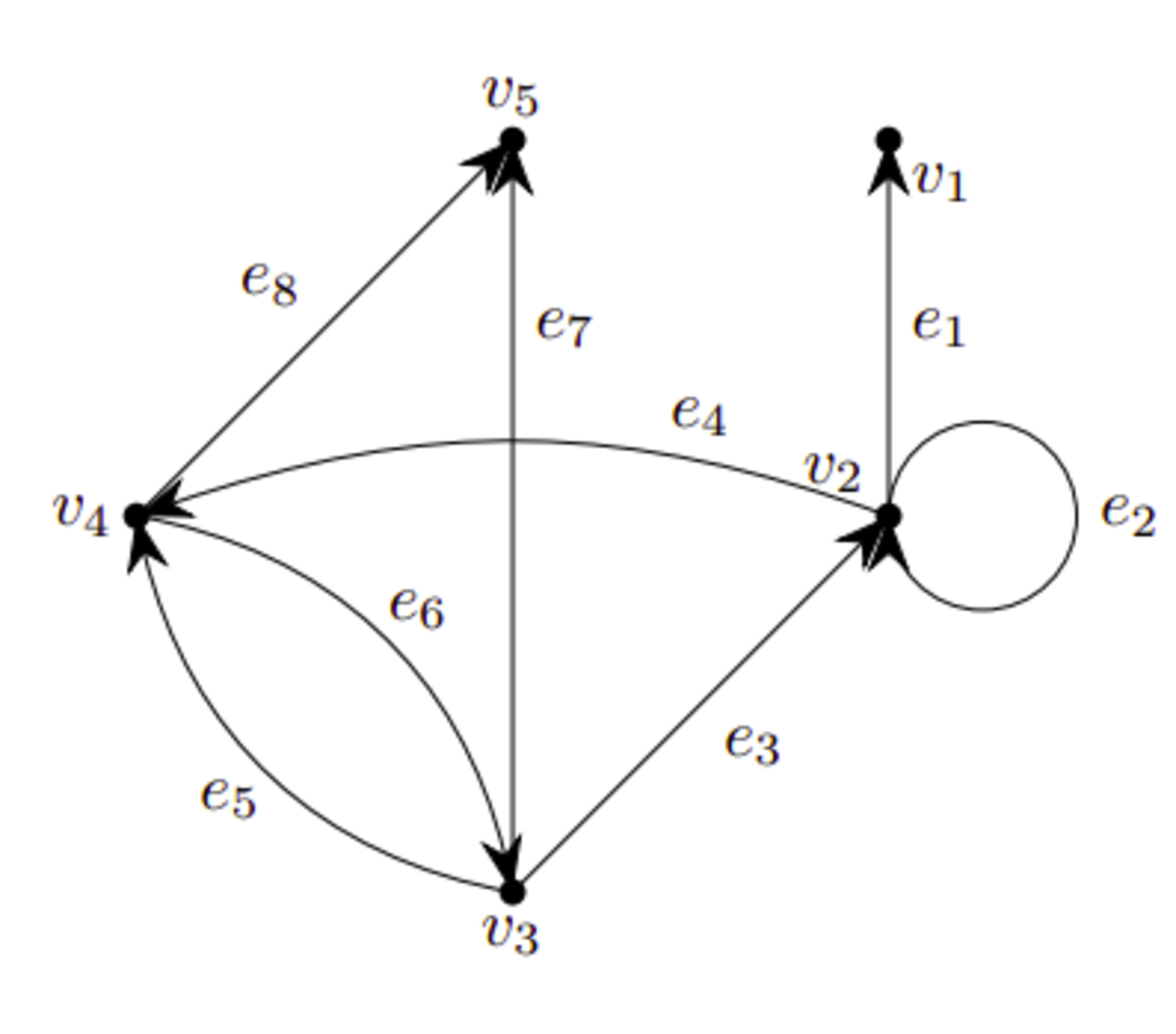有向グラフの例

道

頂点と辺を交互に並べた空でない有限列 $W = v_{0} e_{1} v_{1} e_{2} \dots e_{k} v_{k}$ で各 $i \leq k$ に対し $e_{i} = (v_{i - 1}, v_{i})$ となるものを有向歩道と呼びます。また $v_{0}$ 、 $v_{k}$ を端点と呼び、特に $v_{0}$ を始点、 $v_{k}$ を終点と呼びます。

歩道 $W = v_{0} e_{1} v_{1} e_{2} \dots e_{k} v_{k}$ が相異なる $i, i^{'} \leq k$ に対し $e_{i} \neq e_{i^{'}}$ であるとき、これを有向小径と呼びます。さらに相異なる $j, j^{'} \leq k$ に対し $v_{j} \neq v_{j^{'}}$ であるとき、これを有向道と呼びます。