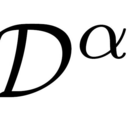sinの弧長とレムニスケートの関係

大学1年生レベル

$\sin$の弧長について

こんばんは、たしです。
今回はsinの弧長についての話です。以前はてなブログでまとめたものの再掲なので、細かい式変形や詳細な説明は省きます。丁寧な記事が見たい方は はてなブログ の記事をどうぞ

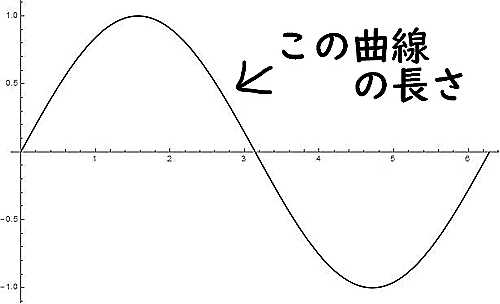sin 長さ

この公式は$f(x)$の弧長が$\sqrt{1+f'(x)}$の積分で求まるという高校レベルの知識から得られます。従って、あとはこの積分を計算するだけなのですが、みなさんはこの積分計算できるでしょうか？

実はこの積分はかなり曲者で恐らく高校範囲では解けません。そこで今回は大学初年度の知識(ガンマ関数、ベータ関数)を用いてこの積分に挑んでみようと思います。

注意: 対称性から、$0<\theta<\pi$の積分が求まれば十分です。
$$\int_0^{2\pi}\sqrt{1+\cos^2{\theta}} \ d\theta = 2\int_0^{\pi}\sqrt{1+\cos^2{\theta}} \ d\theta$$

【略証】

よって、$\sqrt{\sin x }と\frac{1}{\sqrt{\sin x}}$の積分が求まれば良いのですが、実はこの積分はガンマ関数という関数を用いて表すことができます。ガンマ関数の詳細な定義や性質は割愛します。

【略証】

これより、$s=\frac{1}{2}$とすることで
$$\int_0^{\frac{\pi}{2}} (\sin x)^{\frac{1}{2}} \ dx =2\sqrt{\pi} \frac{\Gamma(\frac{3}{4})}{ \Gamma(\frac{1}{4})}$$
$s=-\frac{1}{2}$とすることで、
$$\int_0^{\frac{\pi}{2}} (\sin x)^{-\frac{1}{2}} \ dx =\frac{\sqrt{\pi}}{2} \frac{\Gamma(\frac{1}{4})}{ \Gamma(\frac{3}{4})}$$が得られます。

これで終わりでもいいのですが、実は$\Gamma(\frac{1}{4})と\Gamma(\frac{3}{4})$の比は、さらに有名な数学定数を用いて表すことができます。それがレムニスケート周率$\varpi \ (=2.62205755...)$です。この定数は知らない方も多いかもしれませんが、簡単に言うと円周率の親戚みたいなものです。円に対応する図形にレムニスケートというものがあり、円周率$\pi$に対応するのがレムニスケート周率$\varpi$です。以下の積分からも何となく二つの定数が似ていると思えるのではないでしょうか。

$$\pi = 2\int_0^1\frac{1}{\sqrt{1-x^2}}dx$$ $$ \varpi = 2\int_0^1\frac{1}{\sqrt{1-x^4}}dx$$

このレムニスケート周率を用いると、先ほどのガンマ関数の値は次のように書けます。

【略証】

よって、これを先ほどの結果に代入することで、
$$\int_0^{\frac{\pi}{2}} (\sin x)^{\frac{1}{2}} \ dx =2\sqrt{\pi} \frac{\Gamma(\frac{3}{4})}{ \Gamma(\frac{1}{4})} \ = \frac{\pi}{\varpi}$$ $$\int_0^{\frac{\pi}{2}} (\sin x)^{-\frac{1}{2}} \ dx =\frac{\sqrt{\pi}}{2} \frac{\Gamma(\frac{1}{4})}{ \Gamma(\frac{3}{4})} = \varpi$$
が得られます。

以上全ての結果から、次の結論を得ます。

かなり簡潔に求まったのではないでしょうか。個人的にはsinの長さが、円周の長さ$\pi$ とレムニスケートの長さ$\varpi$を用いて簡単に書けるところに何か奥深さのようなものを感じます。ちなみにこの問題は『楕円積分』と呼ばれるジャンルらしいので、気になる方は調べてみてください。

それでは最後まで読んでいただきありがとうございました。　
もし誤植やミスがあった場合はコメントやTwitter(@math_lewisia)までお願いいたします。