数学で所得格差を考える～ジニ係数～

はじめに

　今回この記事では、統計学に関する内容を扱っていきたいと思います。様々な事をデータ化して分析を行う現在、どんな人でも統計やその周辺の話題について触れないで過ごすことはないですよね。学生であれば、「偏差値」が一番身近な統計データかもしれません。
　その中でも今回は「ジニ係数」について紹介していきます。「ザ・数学」というよりは、少し社会系も混ざった記事になってしまうかもしれませんが、興味を持った方はぜひ最後まで読んでみてください。

ジニ係数とは？

　ジニ係数とは簡単に言うと「格差を表すために使う指標」です。最近ニュースでも使われるようになってきたので聞いたことがある方もいるかもしれません。主に社会において所得格差を測るために使われます。それでは、前置きが長くなりましたが、ジニ係数の求め方を見ていきましょう。

ジニ係数を求めよう

お年玉10万円を5人で分ける場合を例にとって考えてみます。今回はAさん1万、Bさん1万、Cさん1万、Dさん2万、Eさん5万というように分配しました。この分配から、収入の少ない順に並べて、累積人数、累積人数比率、累積収入、累積収入比率を下の表のように求めます。
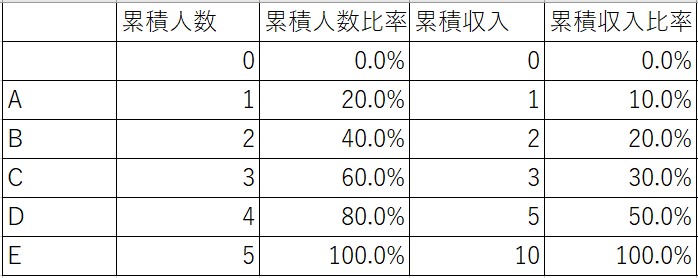　 表１
　次に、この表を使ってローレンツ曲線を描いていきます。

ローレンツ曲線とは

　ローレンツ曲線とは、分配の状態を折れ線で表したもので、これを描くことにより、分配の平等・不平等を目で観察することができるようになります。上の表の累積収入比率を縦軸に、累積人数比率を横軸にとって描いたものが下のグラフです。
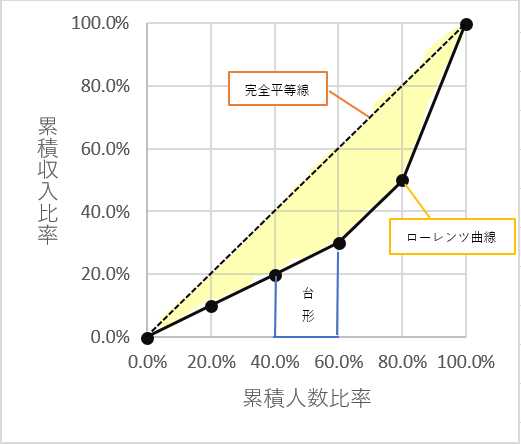グラフ1
　ここで、もし5人に同じ値段ずつお年玉が分配されていた場合について考えてみます。同じ値段ということは2万円ずつになりますね。この時、ローレンツ曲線は、累積人数比率の増え方と累積収入比率の増え方が同じになるので、45度線に等しくなります。これを完全平等線と言い、グラフの中の対角線のような直線になります。
　反対に、もし5人のうち一人だけが10万をもらい残りの4人が1円ももらわなかった場合、ローレンツ曲線は最も下方に位置する折れ線となります。つまり、ローレンツ曲線が完全平等線に近いほど均等に分配されていて、ローレンツ曲線が右下の一角に近いほど不平等に分配されているということです。
　さて、ここまで理解出来たら、いよいよジニ係数の登場です。具体的には、ローレンツ曲線と完全平等線で挟まれた部分の面積が、完全平等線を斜辺とした直角三角形の面積に占める割合で表すことができます。

完全平等線とローレンツ曲線で挟まれた部分とは、グラフの黄色で塗りつぶされたところにあたります。この部分の面積を出すには、グラフにある台形の面積を合計して、完全平等線を斜辺とした直角三角形の面積から引けば求められます。

四角形の面積が1ということは、もちろん
　　0$ \leq $G$ \leq $1
であり、分配が完全に平等であれば、G=0が成り立ちます。反対に分配が不平等になるほどGは1に近づきます。

補足

　さて、これでジニ係数の求め方は終わりです。しかし、今回はあまりにも数式が出てこなかったので、最後に少しだけ発展した内容を紹介しておきます。
　実は、ジニ係数を求めるのに便利な公式があるのです。それがこちら。

　　　　G=$\frac{1}{2n^2\bar{x}}$$ \sum_{i=1}^{n}$$ \sum_{j=1}^n $ |$x_{i}$-$x_{j}$|

実際に今回のお年玉の配分をこれで計算すると…
　　　まず各要素の差の絶対値を全ての組み合わせについて足すと、36。
　　　さらに、$\bar{x}$=$ \frac{1+1+1+2+5}{5} $=2なので
　　　$G_{x}$=$ \frac{36}{2×5^2×2} $=0.36

となります。したがって、この場合ジニ係数は0.36というのが答えです。

　今回は初心者向けにこの記事を書いているので(というのは建前で本当は難しいから…)この公式の証明は省略します。
　興味を持った方はぜひご自分で調べてみてください！また、これをきっかけに、日本の所得格差問題についても関心をもってもらえたら嬉しいです。