5
解説大学数学以上
四平方の定理(記事作成の練習)
$$$$
記事作成の練習も兼ねて四平方の定理の紹介とその証明を書こうかと思います。
(四平方の定理は正式な名前ではありません)
四平方の定理
四面体ABCDにおいて∠BAC＝∠CAD＝∠DAB＝90°の時、
$ △BCD^2 $＝$△ABC^2$+$△ACD^2$+$△ADB^2$
が成り立つ。
証明
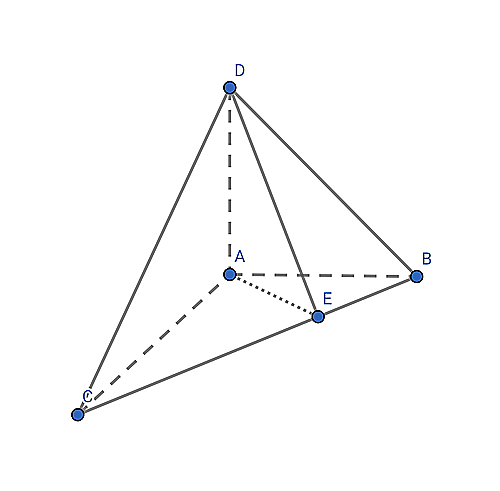図１
BC上にBC$\perp$AEかつBC$\perp $DEとなる点Eを取る。（Eの存在は三垂線の定理から簡単に分かる）
ここで、$△BCD ^2 $＝$\frac{BC^2\times DE^2}{４} $＝$ \frac{1}{4} ${$BC^2 \times (AD^2+AE^2) $}
＝$ \frac{1}{4}$ {$(AB^2+AC^2)\times AD^2+BC^2\times AE^2$}
＝$\frac14$($AB^2\times AD^2+AC^2\times AD^2+BC^2\times AE^2$)
＝$△ABC^2$+$△ACD^2$+$△ADB^2$
(式変形に三平方の定理を用いている)
検算に使えるかもしれませんね。僕は高校受験で面積比と組み合わせて多用していました。
次の記事はピザの定理の簡潔な証明かも、、、
投稿日：2020年11月10日
投稿者
投稿者
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
コメント
コメント