文献あり

特異点論入門〜これほど簡単な入門記事は多分ない〜part1

550

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

特異点論入門 part1

お久しぶりです

こんにちは！！しんぎゅらです！！最近は弊大学で学祭があり,そこで数学科有志企画「数学カフェ・数学おもしろ話コンペティション」というのを運営していましたので,記事が書けていませんでした...
ちなみに私も発表しました.「ライツアウトの〇〇的解法」という記事を元に発表したら、思いの外先生からの評価も高くてびっくりしました！！

さて今回は特異点論について書こうと思います,そうです、私の専門です.

特異点ってなんぞや

まず,イントロダクションです.最初は$2$変数で始めます.
これから微分を前提とするので,$f$はある程度微分可能な関数とします.(後でちゃんと,設定はするのでイントロダクションの間は我慢してね)
以下の定理は大学1,2年生の時に習うと思います.

陰関数定理(Implicit Function Theorem)

滑らかな陰関数$f(x,y)=0$とする. $f(a,b)=0$なる点$(a,b)\in\mathbb{R}^{2}$について,
$\frac{\partial f}{\partial x}(a,b)\neq0$が成り立つ時, $f(x,y)=0$は$(a,b)$の近くで$y=g(x)$という形で書ける.
同様に$\frac{\partial f}{\partial y}(a,b)\neq0$が成り立つ時, $f(x,y)=0$は$(a,b)$の近くで$x=g(y)$という形で書ける.

つまり,陰関数があった時に"ある条件"を満たせば,陽関数として表示できると言う意味ですね！陽関数があれば上手く接線を取ってこれそうですよね
では,その"ある条件"が成り立たないのはいつでしょうか？その時には果たして(滑らかなのに)接線が取れないモノが存在するということでしょうか？

特異点

$f:\mathbb{K}^{2}\rightarrow\mathbb{K}$:滑らかな関数と$(a,b)\in\mathbb{K}^{2}$について,
$\frac{\partial f}{\partial x}(a,b)=\frac{\partial f}{\partial y}(a,b)=0$となるとき,$(a,b)$は$f$の特異点(singular point,singularity)という.

円$x^{2}+y^{2}-1=0$は曲線上の全ての点で陰関数定理の仮定を満たしますね〜
$y^{2}-x^{3}=0$は原点$O$で陰関数定理の仮定を満たしませんね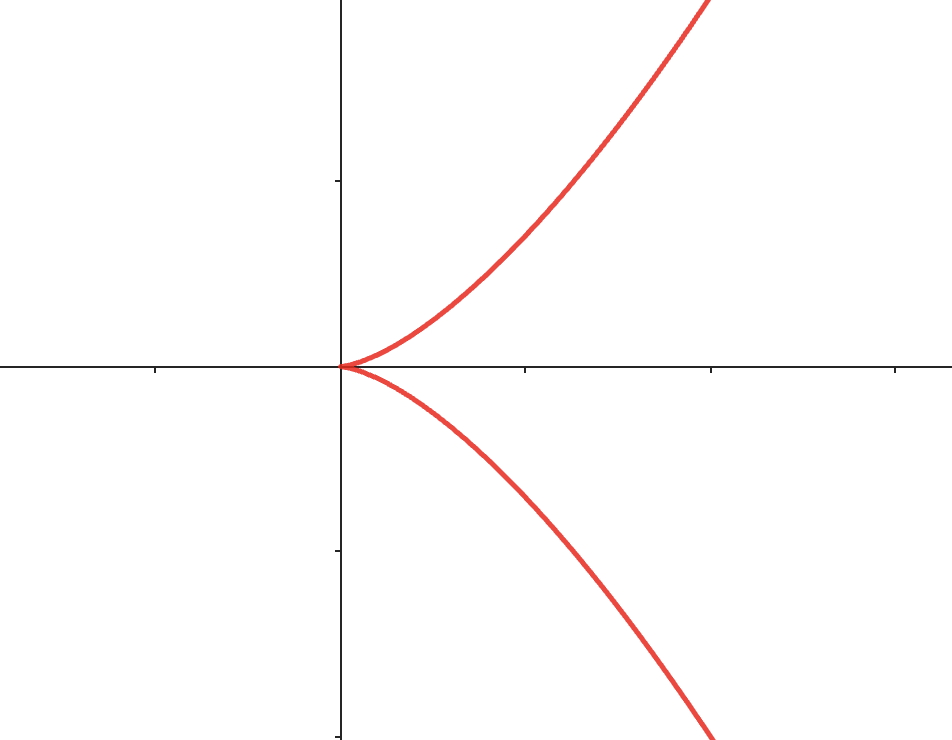尖ってて接せなさそう

数IIBか数IIIで微積分やった人は,関数の性質(増減や極大極小など)を調べたい時には微分して$0$になる点を調べましたよね？そう、実は高校数学でも皆さんは特異点に触れてきたんです！そう考えれば特異点を考えるモチベーションは分かったはずです.

特異点の定義と必要な概念

さきほど$(a,b)$が特異点の定義をしましたが, 必要に応じて平行移動すれば特異点を原点$O$に持って来れるはずです.そして原点に持ってきた方が幾許か楽なので原点$O$に注目して考えます.

集合芽

$(X,\mathcal{O})$を位相空間として,$x\in X$をとる.
$A,B\in\mathcal{O}$について関係$\sim_{x}$を以下で定義.
$A\sim_{x}B\overset{\text{def}}{\Longleftrightarrow}\exists U$:$x$の近傍 s.t.$A\cap U=B\cap U$
このとき,関係$\sim_{x}$は同値関係になる.
この同値関係による同値類を集合芽(set germ)といい,$(A,x)$と書く.

これはデカい集合を考えなくても$x$の近くの小さい集合を考えればいいよ〜という設定です(えらくざっくり)

写像芽

$X,Y$:位相空間,$x\in X$,$M:=\{(U,f)|U\subset X$:$x$の近傍$,f:U\rightarrow Y\}$について,$M$上の関係$\approx_{x}$を考える.
$(U_{1},f_{1}),(U_{2},f_{2})\in M$について,$(U_{1},f_{1})\approx_{x}(U_{2},f_{2})\overset{\text{def}}{\Longleftrightarrow}\exists U\subset U_{1}\cap U_{2}$:$x$の近傍 s.t.$f_{1}|_{U}=f_{2}|_{U}$
この関係$\approx_{x}$は同値関係になり,この同値関係による同値類を写像芽(map germ)という.

こいつも集合芽と同じように,ある点のめっちゃ近くだけ調べる時に使う概念です.ある点の近くで同じ写像だったら,遠くの部分は気にしなくても良いから同一視しちゃおう〜〜！！のノリです(えらくざっくりリターンズ)

また,私は代数学徒です(唐突な自己紹介)そんなそんな$\sin,\cos$とか$e^{x}$をそのまま使うのは面倒です.俺らが好きなのは環とかイデアルなんじゃ〜〜い！！
勘の良いガキの皆さんはお気付きでしょう.そうですTaylor展開されたものを考えます.即ち私は解析的な関数しか扱いませんし,展開された関数(多項式みたいなヤツ)を考えます.

$E_{n,p}\overset{\text{def}}{=}\{f:(\mathbb{K}^{n},0)\rightarrow\mathbb{K}^{p}|f:\text{解析的な関数}\}$
特に$P=1$の時に$E_{n}$と表す.
また,$\mathbb{K}=\mathbb{C}$のとき,$E_{n}$を $\mathcal{O}_{n}$と表す

$E_{n,p}$は加法と乗法に関して環をなします.
特に$E_{n}\cong\mathbb{K}\{x_{1},\cdots,x_{n}\}$:収束冪級数環と言えます.よって局所環であることが分かり,その唯一の極大イデアル$\mathfrak{m}$は$\mathfrak{m}=\langle x_{1},\cdots,x_{n}\rangle_{E_{n}}$になります.
$\mathfrak{m}^{k}=\langle\cdots, x_{1}^{i_{1}}\cdots x_{n}^{i_{n}}$(ただし$i_{1}+\cdots i_{n}=k$)$,\cdots\rangle_{E_{n}}$

(飛ばしてもOK)

アティマク等で可換環論を勉強された方はこう考えるかもしれません
「$E_{n}\setminus\mathfrak{m}$の元って全部可逆なの？」
答えはYes. $E_{n}\setminus\mathfrak{m}$の元$f$は
$f(x)=a+a_{10\cdots0}x_{1}+\cdots+a_{0\cdots01}x_{n}+\cdots+a_{i_{1}\cdots i_{n}}x_{1}^{i_{1}}\cdots x_{n}^{i_{n}}+\cdots$($a\neq0$)と表されるのですが,$g(x)=b+b_{10\cdots0}x_{1}+\cdots+b_{0\cdots01}x_{n}+\cdots+b_{i_{1}\cdots i_{n}}x_{1}^{i_{1}}\cdots x_{n}^{i_{n}}+\cdots$と掛け算して,$f\times g=1$を解くことで
$b=a^{-1}, b_{10\cdots0}=a^{-1}(1-a_{10\cdots0}b),\cdots$と帰納的に逆元の係数たちが求まっていきます.

イントロでやった定義を$n$変数バージョンにしてみましょう！

特異点

$f\in E_{n,p}$とする.
$f$が原点$O$で特異点を持つ$\overset{\text{def}}{\Longleftrightarrow}$ヤコビ行列$Jf$の階数が$n$と$p$のいずれより小さい.即ち,

$\rank\begin{eqnarray} \left( \begin{array}{cc} \frac{\partial f_{1}}{\partial x_{1}}(0) & \cdots & \frac{\partial f_{p}}{\partial x_{1}}(0) \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{1}}{\partial x_{1}}(0) & \cdots & \frac{\partial f_{p}}{\partial x_{n}}(0) \end{array} \right) \end{eqnarray} \lt \min\{n,p\}$

$f\in E_{n}$が原点$O$で特異点を持つ$\Leftrightarrow f\in \mathfrak{m}^{2}$

$f(x)=a+a_{1}x_{1}+\cdots+a_{n}x_{n}+\cdots+a_{i_{1}\cdots i_{n}}x_{1}^{i_{1}}\cdots x_{n}^{i_{n}}+\cdots\in E_{n}$とする.
$f$は原点$O$を通るので,$a=f(0)=0$.
$\frac{\partial f}{\partial x_{1}}(x)=a_{1}+($高次の項$)$となるので$a_{1}=\frac{\partial f}{\partial x_{1}}(0)=0$
同様にして,$\forall i, a_{i}=0$が成立.よって$f\in\mathfrak{m}^{2}$