モーリーの定理
モーリーの定理の初等的な証明です。
 モーリー1
モーリー1
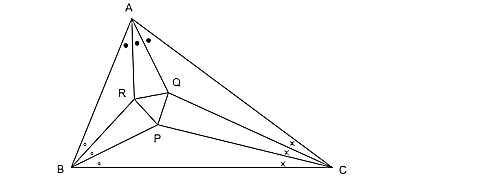
三角形ABCの3つの角それぞれについて、角の3等分線を引く。
隣接する3等分線の交点をP, Q, Rとしたとき、三角形PQRは正三角形である。
 モーリー2
モーリー2
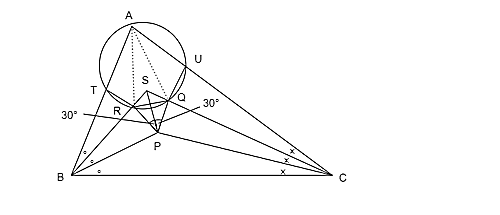
∠A=3a, ∠B=3b, ∠C=3c とする。
∠B, ∠Cの3等分線の交点をP, Sとする。
点Pは△BCSにおける内心となる。よって、線分SPは∠Sを2等分する。
2点Q, Rをそれぞれ線分BS, CS上に
∠SPR=SPQ=30° となるようにとると、△SPR≡△SPQである。
(∠RSP=∠QSP, SPが共通であることに注意)
すると、RP=QP, ∠QPR=60° より、△PQRは正三角形である。
△SQRは二等辺三角形であるため、∠SQR=∠SRQ さらに、
∠SQR+∠SRQ=180°-∠QSR=180°-∠BSC=180°-(180°-(2b+2c))
=2b+2c となるので、
∠SQR=∠SRQ=b+c となる。
ここで、3(a+b+c)=180° から、a+b+c=60° であるから、∠SRQ=60°-a
したがって、∠SRP=∠SRQ+∠QRP=120°-a となる。
次に、線分BA, CA上にそれぞれBP=BT, CP=CU となるような点T, Uをとる。すると、△BRP≡△BRT, △CQP≡△CQU が成り立ち、
TR=RP=UQ=QP …(ⅰ) が導かれる。
次に、∠TRQ=∠TRS+∠SRQ=∠SRP+∠SRQ=180°-2a
同様にして∠UQR=180°-2a から、∠TRQ=∠UQR
3a=∠A$ \lt $180° より、a$ \lt $60°, 180°-2a$ \gt $60°…(ⅱ)
ここで、次の定理が知られている(証明は簡単なので考えてみてください)。
4点A, B, C, Dが次の2条件を満たすとき、これらは同一円周上に存在する。
(1) AB=BC=CD
(2) ∠ABC=∠BCD$ \gt $60°
さらに、∠ABC=∠BCD=180°-2aとおいたときに、直線ADに関して点B, Cと反対側にある点Xが∠AXD=3aを満たすとき、点Xも4点A, B, C, Dと同一円周上に存在する。
(続きから)
よって、(ⅰ), (ⅱ)から、ナラニエンガーの定理より5点A, T, R, Q, Uは同一円周上に存在する。
またTR=RQ=QUより、これらの円周角は等しく、線分AR, AQは∠Aを3等分することが分かる。
Q.E.D.
