グリーン・タオの定理1　グラハム・ロスチャイルドの定理

こんにちは,itouです.
グリーン・タオの定理(著:関真一朗)を買ったので,内容を少しまとめます.
この本では以下の定理を理解することが最終目的です.

このような整数からなる集合がどのような場合に等差数列(やその一般化)を含むかという問題をAPラムゼー問題といいます.(APはArithmetic Progressionの頭文字)

まず,以下の定理が第一歩です.

もし$\mathbb Z_{>0}\backslash\mathbb P$が任意の長さの等差数列を含まないならば,ファン・デル・ヴェルデンの定理よりグリーン・タオの定理が証明されますが,実際はそうではありません.(いくらでも長い素数砂漠が存在することから$\mathbb Z_{>0}\backslash\mathbb P$は任意の長さの公差1の等差数列を含むので)
ファン・デル・ヴェルデンの定理は任意の等差数列を含む部分集合がどれか教えてくれないのです.これを克服するのがセメレディの定理です.ハイパーグラフ除去補題(第4章)⇒有限版多次元セメレディの定理(第2章)⇒多次元セメレディの定理(第2章)⇒セメレディの定理(第2章)という関係があります.つまりハイパーグラフ除去補題を示せばいい(第4章)のですがいきなりそれは難しいので,今回はファン・デル・ヴェルデンの定理の一般化であるグラハム・ロスチャイルドの定理を解説します.これはいわば一般化された等差数列についてのファン・デル・ヴェルデンの定理です.注:この定理はグリーン・タオの定理の証明に使われません.準備運動というわけです.

記号について

通常と違い,$[a,b]$は$a$以上$b$以下の整数の集合を指します.また,$[N]=[1,N]$とします.等差数列$(a)_n$と集合$\{a_1,a_2,\cdots,a_n\}$を同一視します.等差数列の元の個数を長さということがあります.

本題

次のような同値関係を導入します.

少し説明しておきます.
同値類とは同値関係によって集合を分類したものです.左から数えて最後に$k$が現れるのを$j$番目とすると,
$j=0$のときの同値類は集合$[0,k-1]^d$です.(元の個数は$k^d$個でそのような同値類は1個)
$j=1$のときの同値類は$\{k,\underbrace{\cdots\cdots\cdots\cdots}_{\text{[0,k-1]の元が}d-1\text{個}}\}$($\cdots$の部分は$k-1$以下の非負整数が並ぶ)の形の元全体の集合です.(そのような同値類はただ1つある.)

同様に$j$のときの同値類は$\{\underbrace{\cdots\cdots\cdots\cdots}_{\text{[0,k]の元が}j-1\text{個}},k,\underbrace{\cdots\cdots\cdots\cdots}_{\text{[0,k-1]の元が}d-j\text{個}}\}$の形の元であって,左の$\cdots$の部分が一致しているような元全体の集合です.(元の個数は$k^{d-i}$個でそのような同値類は$(k+1)^{j-1}$個ある.)

このように$[0,k]^d$を$1+1+(k+1)+(k+1)^2+\cdots+(k+1)^{d-1}$個の集合に分類しておきます.

以下の同値関係$～$は$k$同値とします.

記号がいっぱい出てきたので整理しましょう.$d$は次元,$m$は分割の個数,$r$たちは公差です.
\begin{multline} \begin{split} \left\{ b+\sum_{j\in [d]}a_jr_j \in [N]:(a_1,…,a_d)\in A \right\} \end{split} \end{multline}
とは$d$次元の等差数列です.(1次元の等差数列がふつうの等差数列です.)等差数列の長さは同値類$A$の元の個数に対応します.($r$たちの値によっては異なる$(a_1,…,a_d)$に対して同じ値であることもあり得るのではと指摘されました.等差数列の長さは最大で$\sharp A$です)$k$は$a_j$の上限で,これより大きくなることはできません.$(a_1,…,a_d)$たちはいわばインデックスで,$(a_1,…,a_d)$たちが同値類$A$の中を動き回ることで数列が作られます.$b+\sum_{j\in [d]}kr_j\leq N$という条件は,これら等差数列の元の中でも一番大きいもの($a_j\leq k$なので)が$N$以下であるようにしたいということです.そのための$N$の条件が$N \geq N_{GR}(k,d,m)$です.そして$[0,k]^d$という空間を$k$同値によって分類し,任意の同値類$A$の元すべてから等差数列の集合を作ると,それは分割のどれかに入ります.それがどの部分集合なのか明示されていないことに注意して下さい.まるで鳩ノ巣原理ですね.(実は証明には鳩ノ巣原理が出てきます.)

証明の方針

正整数$k,d$を固定し任意の$m$に対し上の主張が成立することを$GR(k,d)$と表すことにします.$k,d$についての二重帰納法で示します.つまり仮定から別のうまい分割を構成します.

ステップ１$GR(k,d)⇒GR(k+1,1)$ を示す

まず,任意の$d\in \mathbb Z_{>0}$に対して$GR(1,d)$が成立することは$[0,1]^d$の任意の２元が互いに1同値でないことより分かります.($N_{GR}(1,d,m)=d+1$とすればよい)

さて,$k$を固定します.以下任意の$d$に対し$GR(k,d)$の成立を仮定します.任意の$m$に対して$N_{GR}(k+1,1,m)=2N_{GR}(k,m,m)$を取ることで,$GR(k,d)⇒G(k+1,1)$ を示します.$M=N_{GR}(k,m,m)$とします.
$N\geq 2M$を満たす$N$と任意の分割$[N]=C_1\cup …\cup C_m$をとり,それから分割$[M]=\bigcup_{i\in [m]}(C_i\cap [M])$をとります.仮定より$[M]$の分割に対して$GR(k,m)$を適用できて,

が成立します.ここで
\begin{multline} \begin{split} b+\sum_{j\in [p]}kr_j (p\in [0,m]) \end{split} \end{multline}

の形の元を考えます.換言すれば,

$\underbrace{(k, \cdots ,k}_{p \text{個}},\underbrace{0,\cdots,0)}_{m-p\text{個}}\in [0,k]^m$
に対する等差数列を考えます.$p$は$0$以上$m$以下なのでこのような等差数列は$m+1$個あり,すべて互いに異なる同値類の元です.分割$[N]=C_1\cup …\cup C_m$は$m$個の部分集合を考えていたのでした.よって,鳩ノ巣原理より,
\begin{align} &b+\sum_{j\in [s]}kr_j \in C_I　　\tag{1}\label{1}\\ &b+\sum_{j\in [t]}kr_j \in C_I \tag{2}\label{2}\\ \end{align}

が成り立つような$s,t\in [0,m](s< t)$および$I\in [m]$が存在します.このとき,任意の$l\in [0,k]$に対して,

\begin{align} &b+\sum_{j\in [s]}kr_j +l\sum_{j\in [s+1,t]}r_j\in C_I \tag{3}\label{3}\\ \end{align}

であることを示します.
$l\in [0,k-1]$のとき,

$\underbrace{(k, \cdots ,k}_{s\text{個}},\underbrace{l, \cdots ,l}_{t-s\text{個}},\underbrace{0,\cdots,0)}_{m-t\text{個}}\quad l\in [0,k-1]$
という元たちはすべて互いに$k$同値なので仮定と\ref{1}より従います.
$l=k$のときは\ref{2}から従います.
これで\ref{3}が示されました.なぜ\ref{3}の形の元を考えたのでしょうか.
それは,

\begin{align} &b+\sum_{j\in [s]}kr_j +l\sum_{j\in [s+1,t]}r_j\in C_I \tag{3} \\ \end{align}
(再掲)この式の
\begin{align} &b+\sum_{j\in [s]}kr_j \\ \end{align}
の部分を初項,
\begin{align} &\sum_{j\in [s+1,t]}r_j \\ \end{align}
の部分を公差とみることで,$k+1$,次元$1$(つまり等差数列の長さが$k+1$)のときに帰着できるからなのです.
次元が1なので,$k+1$同値の同値類は二つしかありません.
つまり,$\{l: l\in [0,k]\}$と$\{k+1\}$です.

\begin{align} &b+\sum_{j\in [s]}kr_j +(k+1)\sum_{j\in [s+1,t]}r_j \\ \end{align}
が$N$以下であることを確かめましょう.
\begin{align} &b+\sum_{j\in [s]}kr_j +(k+1)\sum_{j\in [s+1,t]}r_j \\ &=\left( b+\sum_{j\in [t]}kr_j \right)+\sum_{j\in [s+1,t]}r_j\\ &\leq M+M\leq N \tag{4}\label{4} \end{align}

$\{(l)| l\in [0,k]\}$については\ref{3}と\ref{4}より,
$k+1$のときは等差数列の元が一つしかありませんから,この等差数列(というか一つの数)が分割のどれかに含まれることは明らかで,\ref{4}と合わせて分かりました.

よって,$GR(k,d)⇒GR(k+1,1)$ が示されました.

ステップ2 $GR(k+1,d)⇒GR(k+1,d+1)$を示す

$GR(k+1,d)$が成り立つと仮定します.
$N_1=N_{GR}(k+1,d,m),N_2=N_{GR}(k+1,1,m^{N_1})$とします.このとき,$N_{GR}(k+1,d+1,m)=N_1N_2$を取れることを示します.
ステップ1と同様に,仮定から別の分割を構成していきます.

$N\geq N_1N_2$を満たす$N$と分割$[N]=C_1\cup …\cup C_m$を任意にとります.
$[N_1N_2]$を
\begin{align} [N_1N_2]=\bigcup_{h\in [N_2]}([N_1]+(h-1)N_1) \end{align}
という$N_2$個の区間に分割します.
以下の通り.
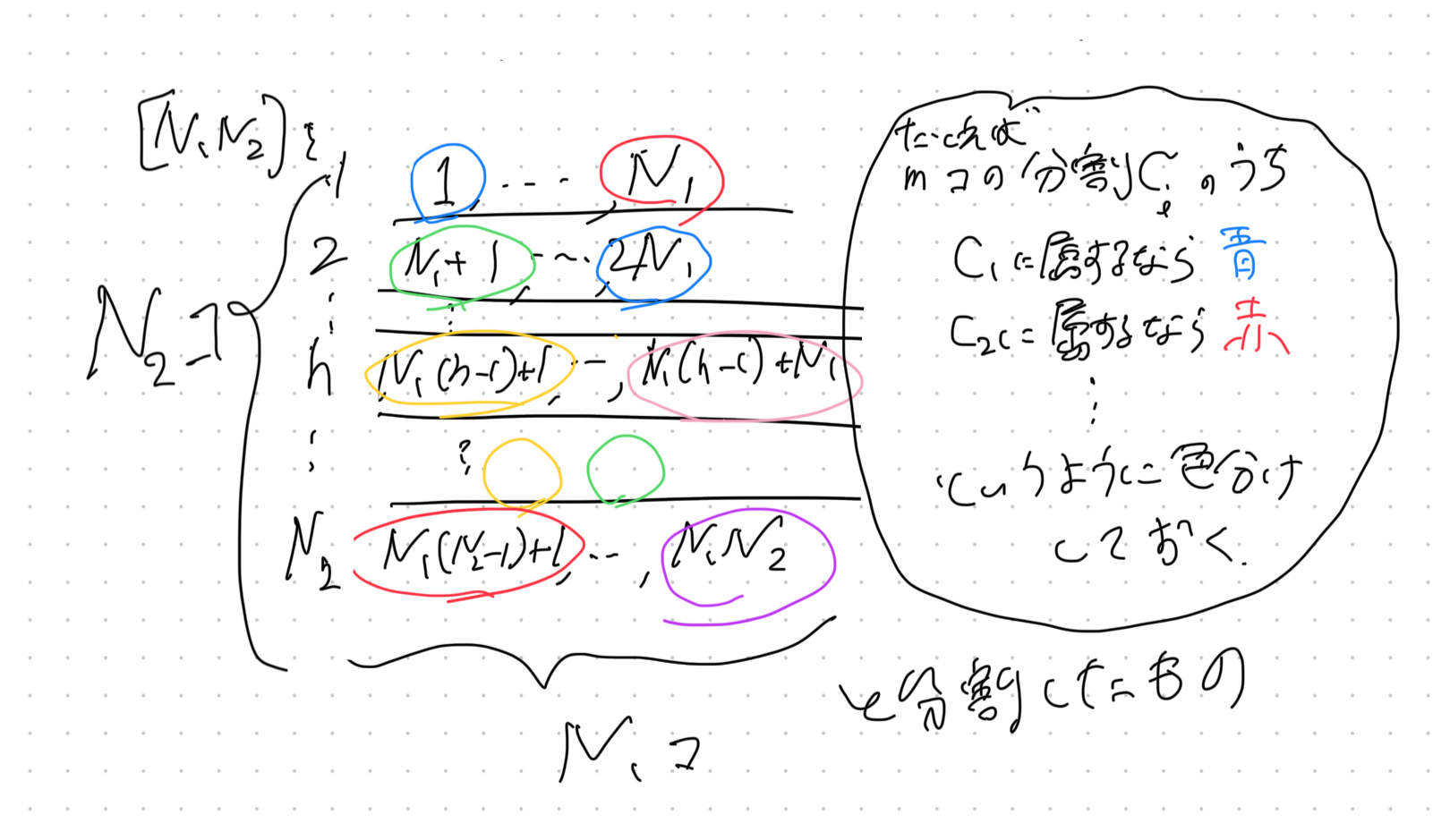図1

上の図で各行は$[N_1]+(h-1)N_1(h\in [N_2])$と表されます.
上の色分けにおいて$N_2$は各行の色分けの総数$m^{N_1}$より大きいので,ある色分けが存在して,その色分けに対応する$h\in [N_2]$が複数存在します.このことを使って逆に$[N_2]$を分割しましょう.

写像$c:[N]→[m]$を$c(a)=$「$a\in C_i$なる番号$i$」として定義し,写像$\textbf{c}:[N_2]→[m]^{N_1}$を
\begin{align} \textbf{c}(h)=(c(1+(h-1)N_1),c(2+(h-1)N_1),\cdots,c(N_1+(h-1)N_1)) \end{align}
で定義します.

このとき,$[N_2]$の分割

\begin{align} [N_2]=\bigcup_{\mathbf j\in [m]^{N_1}}(\textbf{c}^{-1}(\mathbf j)) \end{align}
が得られます.

よって,$N_2$の定義から$b'+(k+1)r'\leq N_2$を満たす$b',r'\in \mathbb Z_{>0}$,$\textbf{i}=(i_1,\cdots,i_{N_1}) \in [m]^{N_1}$が存在して,
\begin{align} \{b'+ar':a\in [0,k]\} \subset \textbf{c}^{-1}(\textbf{i})) \end{align}
が成り立ちます.
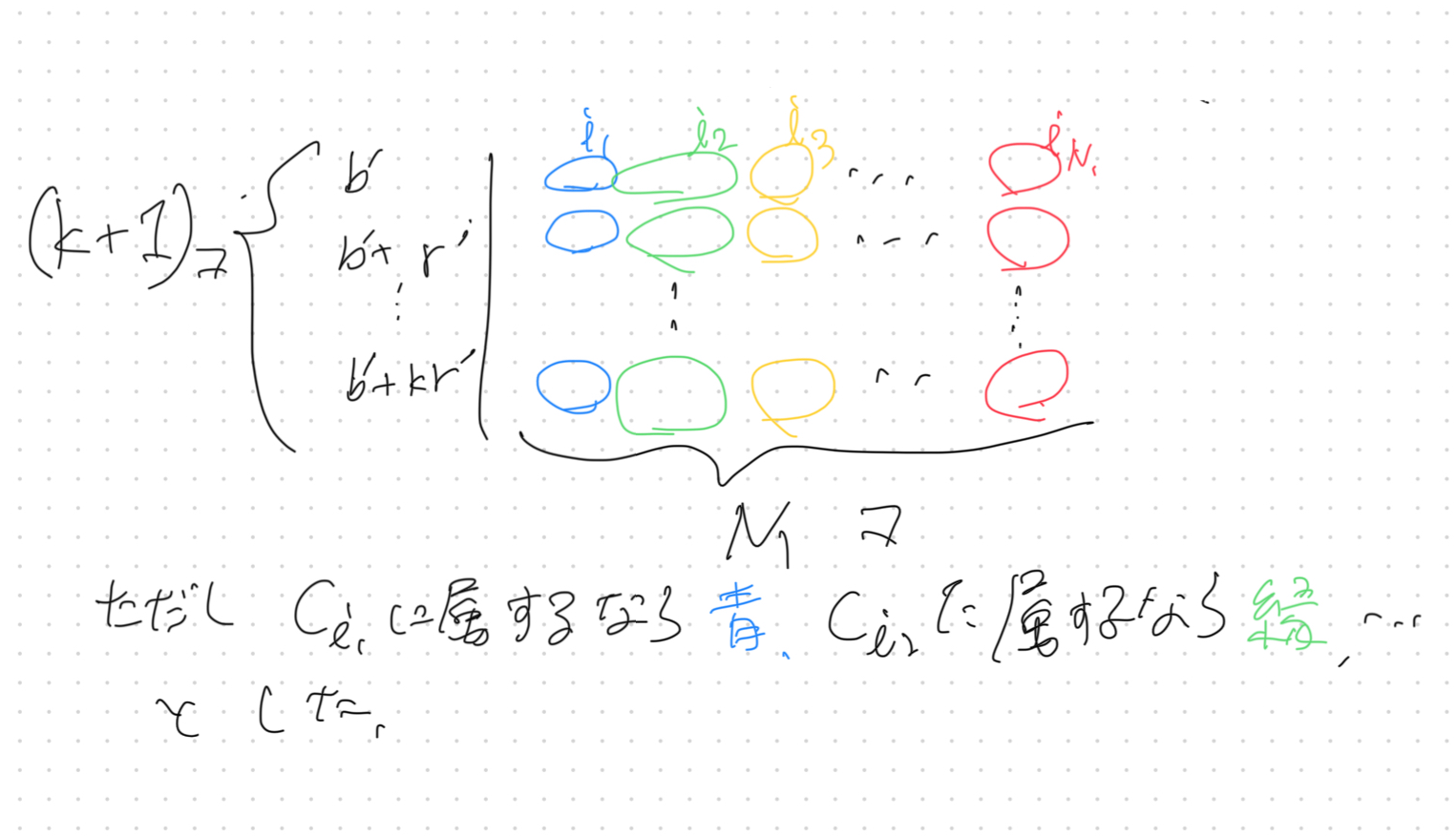図2

$N_1$は$m$よりも十分大きいので,$i_j$の中には同じものが複数含まれうることに注意して下さい.

従って
各$l\in [N_1]$に対して
\begin{align} \{l+(b'+ar'-1)N_1:a\in[0,k]\}\subset C_{i_l}\tag{5}\label{5} \end{align}
であることが分かります.

ここまで来たらもう少しです.最後にある$L\in [N_1]$が存在して$C_{i_L}$の中に所望の$(k+1,d+1)$の等差数列が含まれることを確認しましょう.

ここで以下の補題を示します.

$GR(k+1,d)$は平行移動の原理を満たすので,$N_1$の定義より区間$[N_1]+(b'-1)N_1$に対して$GR(k+1,d)$を適用することで(ここでようやく仮定を使います)
\begin{align} (b'-1)N_1+1\leq b+\sum_{j\in [d]}a_jr_j \leq b'N_1,\quad (a_1,\cdots a_d)\in [0,k+1]^d \end{align}

を満たす$b,r_1,\cdots r_d$が存在し,$[0,k+1]^d$の$(k+1)$同値に関する各同値類$A$ごとに$i(A)\in[m]$があって

\begin{align} \left\{ b+\sum_{j\in [d]}a_jr_j :(a_1,…,a_d)\in A \right\}\subset C_{i(A)}\tag{6}\label{6} \end{align}

が成立します.このとき,
\begin{align} &b+\sum_{j\in [d]}(k+1)r_j +(k+1)r'N_1\\ &= b'N_1+(k+1)r'N_1 \\ \tag{7}\label{7} &\leq N_1N_2\leq N \end{align}
であることに注意して,$[0,k+1]^{d+1}$の$(k+1)$同値に関する任意の同値類$A'$に対して$i'(A')\in [m]$が存在し,

\begin{align} \left\{ b+\sum_{j\in [d]}a_jr_j +a_{d+1}r'N_1:(a_1,…,a_d,a_{d+1})\in A' \right\}\subset C_{i'(A')}\tag{8}\label{8} \end{align}
が成り立つことを確認しましょう.$A'$は$[0,k+1]^d$の$(k+1)$同値に関する同値類を用いて$A'=A×[0,k]$と表されるか,第$(d+1)$成分が$k+1$であるような1元集合です.後者の場合は自明(同値類の元が1つ,つまり等差数列の長さが1だから)なので,前者の場合を考えます.$(a_1,\cdots ,a_d)\in A$
を固定するとき,\ref{5}により,
\begin{align} \left\{ b+\sum_{j\in [d]}a_jr_j +a_{d+1}r'N_1:a_{d+1}\in [0,k] \right\}\subset C_{i_L}\tag{9}\label{9} \end{align}
が成り立ちます.ただし$L=b+\sum_{j\in [d]}a_jr_j-(b'-1)N_1\in [N_1]$です.

$A'=A×[0,k]$でしたから,$A'$は$A$の元に$(d+1)$番目の元を付け加えて作ったのでした.\ref{9}はそのようにして作った$A'$から作った等差数列がすべて同じ$[N]$の分割の部分集合に入ると言っています.
ここで,以下のことに気をつけてください.

$a_{d+1}=0$のときを考えます.(いま$(a_1,…,a_d)\in A$を固定していることに注意)
\begin{align} \left\{ b+\sum_{j\in [d]}a_jr_j :(a_1,…,a_d)\in A \right\}\subset C_{i(A)} \end{align}
\begin{align} \left\{ b+\sum_{j\in [d]}a_jr_j +a_{d+1}r'N_1:a_{d+1}\in [0,k] \right\}\subset C_{i_L} \end{align}

上の2つの集合にはともに固定した$(a_1,…,a_d)$に対し
\begin{align} b+\sum_{j\in [d]}a_jr_j \end{align}
が含まれています.よって,上の囲み枠より,$i(A)=i_L$です.
最後に$(a_1,…,a_d)$を動かしますが,$L$は$(a_1,…,a_d)$に依存していました.$\sharp A$個の$(a_1,…,a_d)$について,$i_L$が同じになります.

結局,つねに$i'(A')=i(A)=i_L$ととれることが分かりました.以上より$GR(k+1,d+1)$が成立します.

感想

二重帰納法とか出てきて楽しかったです.$N_{GR}(k,d,m)$がどのような整数になるんでしょうか.ちなみにこの内容は本書で3ページくらいです.先は長いですね.

謝辞

ここまで読んで下さりありがとうございました。誤植等指摘お願いいたします。

訂正記録

2024/04/14:$k$同値の例,誤植を訂正
2024/04/17:$k$同値の同値類の個数の誤りを訂正,等差数列の長さについての指摘を反映,最後の$i'(A')=i(A)=i_L$を得る議論を修正.