まいんの数オリ体験記後編

前編の記事は こちら
後編では2023年の春合宿とIMOについて詳しく記し、加えて競技数学を志すみなさんへ少しメッセージを書いています。

春合宿2023

問題: https://www.imojp.org/archive/mo2023/selection_camp/problems/2023.pdf

待ちに待った春合宿2023がやってきました！！！！！！

この頃には、だいたい感覚としては自分はかなり分野の偏りが小さい方ではあるもののCは少し苦手でFEが得意かもな、くらいに思っていました。
そうすると2C3FEだったときのムーブに困るな...と思いますがやはり2番の方を重視する方向でいこうという戦略を立てました。

Day0 (3/19)

この日は表彰式がありました。全体の半分以上が知り合いの人でびっくりした。自分も随分と数オリをやってきたんだな...と感慨にふけっている暇もなく春合宿が始まってしまいました。
本選の答案用紙とAPMOの答案用紙・結果が返却され、もう嘘と減点だらけの解答に発狂しました。特にAPMOは嘘をつきすぎて下から6番に入っており、逆IMOの代表になれるななどと訳の分からないことを考えて、本選も予期してはいたものの華麗なる嘘で3年連続メダルを逃し、まあでもこれらのコンテストは自分にとっての優先度が高くないわけで、春合宿に残れたからまあいいかという気分になりました。気持ちの切り替えは大事ですね。
実際本選でもAPMOでもやらかしていますが自信はありました。というのも春合宿が3回目なのは後のJPN4,5と僕だけで、経験は十分積んでいる。また自分は今まで春合宿に照準を合わせてきたのだからきっと大丈夫(?)という謎の自信がありました。とにかく自信はありました。

Day1

午前中は演習でした。楽しいですね。WBCが盛り上がっていました。日本代表として戦っている姿はかっこいいですね。

午後が試験なので昼はあまり食べれない。

試験day1

春合宿2023day1

分野はNCA。かかってこい！！！！
問題を開くとマス目の問題があってちょっとビビる。

まず1Nを考える。実験をする。
ある二数が共通素因数pを持つとき、この二数がp以上離れてないと全部がpの倍数になってしまい困る、というおおまかな構造がすぐに見えたのであとは場合分けを詰めるだけとなった。
場合分けが多いがまあ1Nというのはそういうものだろうという気分。同じ1Nでいえばイギリス選抜の方がよほど記述量は多いわけで、慣れたものですね。1時間ほどで解答を書きました。

次に2Cを見る。マス目というのはちょっと怖いが、評価と構成を与えるタイプは得意なので救い。
このタイプの問題のキーは「オーダー評価が難しい場合があるので、うまくいかないときは上と下から緩すぎると思う上界・下界を見つけ、少しづつ狭めていく」ということだ。これをすれば間違ったオーダーに固執することがなくなる。これはIMO2022-6から学んだ教訓である。

真っ先に思いつくのがL字を重ねていくやつで、これをすればn/2オーダーが達成できる。この評価をしようと考えるとやはり中央の列の取り合いに注目することになるが、それだけだとうまくいかない。
ここで1時間くらい考えるが、まだ実験をまともにやっていないことに気付く。あぶなかった。実験をやり直すと、n=7のときに別の構成が見えてきた。いろいろ試してみるとL字を四方から囲んだような構成が浮かび上がり、これによって4n/3オーダーが達成できることに気付いた。隠れ構成には要注意。
評価をしよう。評価をする時のポイントは
「構成の特徴を見つめ、どこに注目するべきかを探し出す」
ことである。とまあ今回はこれは使わず、先ほどやりたかった「真ん中の方を取り合っててもう満席なんだけど！」という評価をしよう。

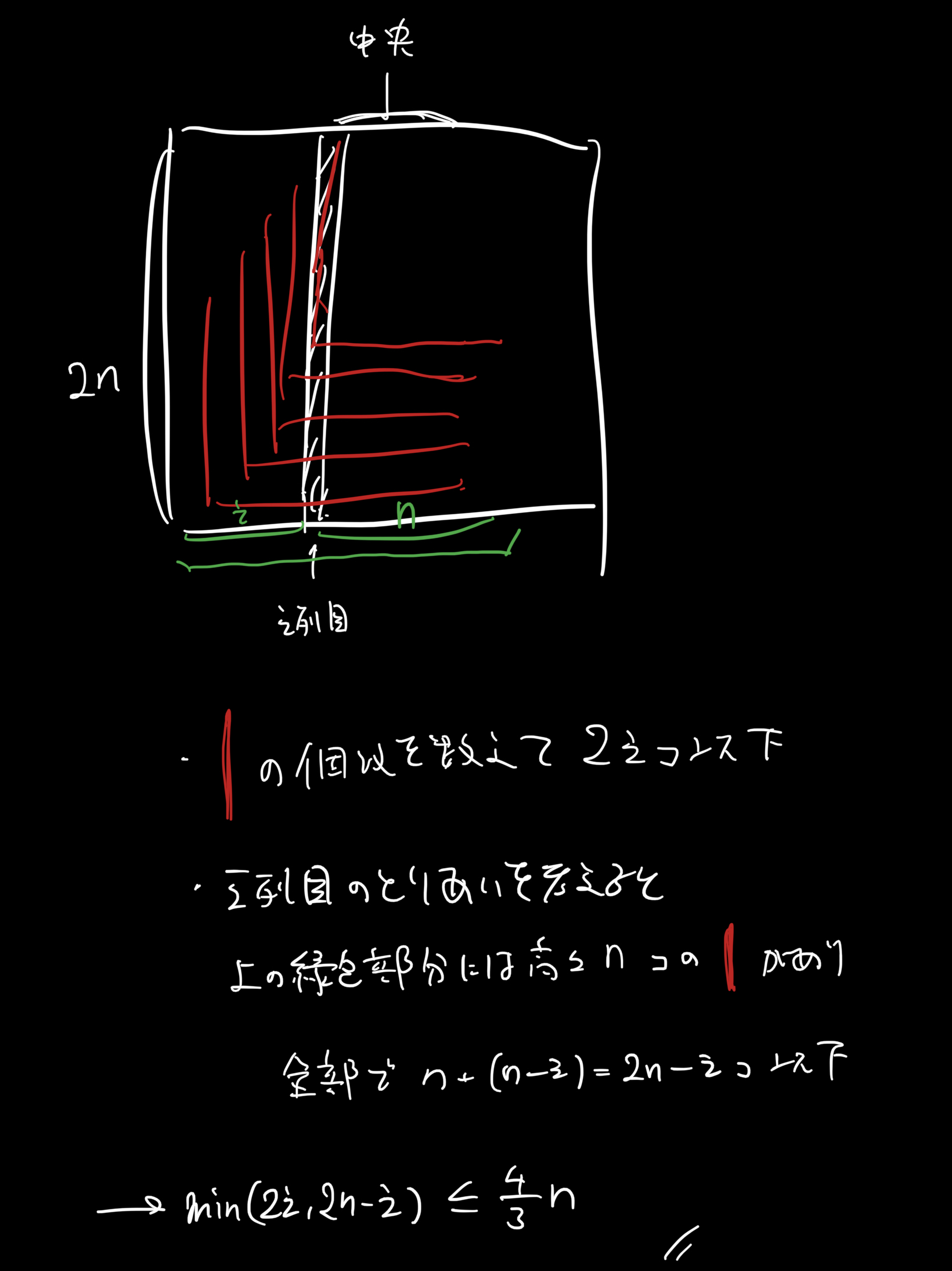問2の概略

無事評価ができました。2Cが解けたのは嬉しいね。

残り1時間で3を考える。また構成と評価か。どっちか簡単な方は取りきりたいな。
ちょっと実験してみるとすごく条件が強いことが分かる。具体値も与えられてないことから、かなり小さめの値なのかな。
ちょっと手を動かすとn=4で構成が見つかる。かなりうまい感じの構成だしこれが最適なのかな。
この後nが5以上の時の証明を試みたけどあまりうまいこと行かず、day1終了

【感想】
試験終了後, 1の値を一つ抜かしていることを知って青ざめた。これはすなわち早速嘘をついたことを意味しているのである...
それでも2を解いている人が少なさそうだったのでなんとか耐えた。何より2Cが早々に消えたのがでかい。
571くらいかなという印象だった。

Day2

春合宿2023day2

分野はGACかな(実はNだった)。6が無理そうな見た目をしているなあ。
4はすぐ解けた。春1Gというのは毎年易しめな印象がありますね。
5は不思議な見た目ですね。よく見たら
「fはImf上で周期的」ということを言ってるんですね。
Imfは加法で閉じているので、Zとして設定するのが最も自然なのかな。そうすると条件式が単純になって、あとは図を書いてどうにかしたいところ。
1周期で整数値のみを値に取るfを考えればいいことになる。図を書くとガウス記号の面影のある図が出てくる。それにしてもこれかなり自由度が高いからさすがに0だけなんじゃないかという気がしてくる。
次々に反例を作っていくことで簡単な大小評価により2より大きい範囲などはダメということがわかる。
とここで、問題文に与えられている「有理数q」を求めよという制約が引っかかる。今自分が考えていることはこれが実数でも成り立つわけで、なぜ有理数の話をしているのか...？
いろいろ試してみると2とか3/2とかはどうしても通ってしまうことが分かって、すなわち(n+1)/nなら必ず通ることが分かった。
これらは本当に必ず通るのかなと考えてみると、f(0)周りを考えることであっさりと示せた。これで解けたのかな。

とこの時点で残り30分。見直しをしたら残り5分ほどになったので、6はほとんど考察できずに終わった。

【感想】
770かなという感じ。ここまでで4問解いている人は6人未満っぽかったので安心した。順調ですね。
夜に残りの分野を考えたら、AGCの日とCNGがあることが分かった。AGCの日は1A2Gの二完、CNGの日は1C2Nの二完を目指していこうという戦略だった。

Day3

春合宿2023day3表
春合宿2023day3裏

衝撃的なことに両面印刷らしい。去年のDay3のような怖さがある。
分野はCNGだ。ここが勝負どころだね。
7を見る。どうやっても解けそう。
8を見る。問題文が長くてよくわからない。
9を見る。図を書いて唖然とする。
「これ直交座標で解けない？」
怖かったので二等分は内角の二等分なのかを質問してしまった。YESとの返事だったので計算をした。意外に手こずってしまったが、直前に直交座標の計算には触れていたので1時間くらいで解き終わることができた。
3番級が1時間で終わるととても気持ちに余裕ができる。続く1時間で7を解いた。
残り2時間半で8か。また去年の8Cみたいに怖い問題なのかな、と問題文の解読をしていると見掛け倒しであることに気付く。というのもこの問題、modpの世界に落とし込むと加減乗除ができるということを言っていて、これでできる操作は一次分数変換と等しいことが知られているため、あとは文字で置いて処理するだけになった。コーナーケースの処理は手こずってしまったが、なんとか時間内に解答することができた。

【感想】
777かな。全完というのは気持ちがいいですね。幸せです。
りぼーすも3完と言っていたが、他に3完の人は見当たらなかった。そもそも僕とりぼーすはここまでで7完ほど取っており、例年のボーダーとされる6完半をすでに超えていてびっくりだった。
正直ここまで来れば代表はなれそうな気もするが、Day4には2Gが残っていたのでそれが楽しみで仕方なかった。

コンテスト終了後は9の件で荒れていた。

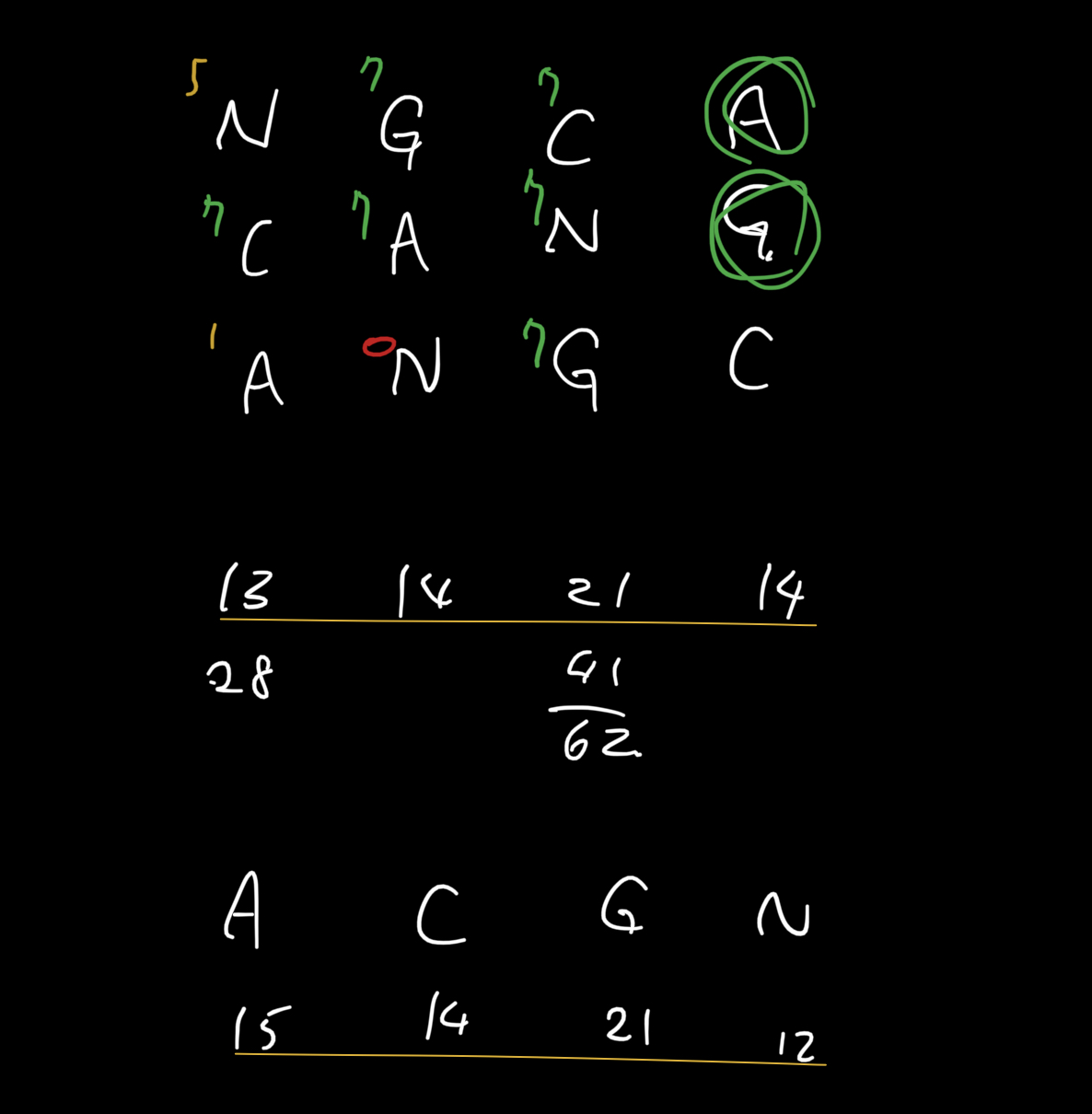Day3が終わった時のメモ。かなりいい感じ？

Day4

春合宿2023day4

分野はすでに分かっており、AGC。2完すれば大丈夫だろう。

1Aを見る。標準的な1Aで、普通の問題だったので1時間くらいで解けた。
次に2Gを見る。2Gなんだからどうせ回転相似だろうと思いながら考えていたら無事回転相似が見つかって安心した。
「分からない線は伸ばす」(by まいん)に従っていろんな直線と円との交点をとっていたらうまくいった。
3Cは構成だけやった。

【感想】
770かな。全部で9完だしおそらく通ったでしょう。自分含め8完以上を主張していた人が5人もいたので異常回なのかなとも思ったが、おそらく6人目は少し点数が離れて密集している様子だった。

結果を見ると61点だった。
Gが一部Gじゃないのはおいといて、やはりNの嘘をついてしまったことが悔やまれた。しかし、代表選考は通ることが目的なのでひとまずいい結果で安心した。

春合宿～IMO

春合宿が終わり、しばらくは春合宿ロスに明け暮れていた。しかし息つく間もなく通信添削や強化合宿が始まり、あわただしい日々だった。
6月になるとIMOが近づいてきたためUSAのコンテストをやった。Evan Chenの解説も丁寧で、面白い技法に日々感心していた。

気づいたら7月、IMOがやってきました。

IMO2023

Day1

問題は こちら から見れます。
2023年の行で言語をJapaneseにすることで日本語の問題文が手に入ります。
IMO2023day1

試験中のムーブ

分野はNGN?...ではなくNGAか。AG好きの僕としては嬉しいセットだ。
まず1を解く。 以下がファーストインプレッションだ（解答用紙から引用。）

よく見ると約数の順番は固定されているので、条件が強すぎることが分かる。ということはうまいところを見つけてきて記述する感じなのかな...と考えていたら2番目に小さい素因数とその周りに注目すればできた。
ここまで30分。1番級は45分を目標にしていたのでかなりいいペース。

次に2を見る。

いつも通り二等分線は内角のなのかを質問するとYESの返答。BSとPでの接線の交点(Xとおいた)は宙に浮いているので、二等分線は劣孤弧BCの中点とAを結ぶ直線として定義するのかな　などと思う。
主人公はさすがに$\Omega$なので,そっちの方に引き寄せていきたい。まずは角度計算をすることでP,D,(Aの対蹠点)が共線であることが分かる。
次に $\omega$を消したいなという気分になる。実際点Lはお飾りであって、PXと$\Omega$の交点をQとすればSQ//PDがわかる。これで完全に$\Omega$上の問題になった。
円上の平行線がたくさん現れて、初等であと一歩だと思って30分ほど格闘するがどうもうまくいかない...とそのとき複素を思い出した。なぜ最初から複素をしなかったのかという気分になったが、最初に書いた方針リストに複素が入っていなかったからであろう。まあここまででまだ1時間15分くらいなので、ここから先が一瞬であることを見た僕はそんなに焦らなかった。
複素があまりにも軽かったので15分で解答を書き上げ、残り3時間弱となった。いいペース！！

3を見る

え、ってかこれAなの？そしたら数列的な見方をするのが良さそうで、そうすると一番現実的なのが大小評価なのかな。
隣り合う式を比較すると$a_1$と$a_2$の大小関係は$a_2$と$a_{k+2}$の大小関係に一致することが分かって、これをいじればすんなりと狭義単調増加の場合に帰着された。Pが非負の係数であることを使えたので嬉しい。ここまではいいペースだが、ここからが本質なんだろうな。
ところでこの場合の解ってあるのかな。ないとしたらオーダー評価で矛盾なんだろうけどどうにもうまくいかないなあ。
あああああ嫌な予感がする。この数列にはやれることがたくさんあって、例えば隣り合う項の商はもう見たけど他にも隣り合う項の差とかオーダー評価であるとかより整数的にみて$a_2| P(a_1)$などの条件を取り出すとか...これらのうちどれが刺さるかを時間内に当てるゲームになってきた。
この中だったらどれがいいだろうと考えると、やはりA分野であるという事実を信じて隣り合う項の差を見るのが賢明だろう。実際項の商と差を順にみることで解けるというのはかなり面白い部類に入るのではないか。
そこで$a_{n+1}-a_n$を見てみると、なんと十分先においてはこれの-1倍がPの根になることが分かった。同様にして$a_{n+i}-a_n(1\leq i \leq n)$も同じことが成り立つことが分かった。もうあと一歩なのでは？
ここからすぐに導かれることとして
\begin{equation} P(x)= \prod_{i=1}^{n}{(x+id)} \end{equation}
がわかり、かつ$a_i$は十分先において公差$d$の等差数列になっていることがわかった。
解答を書き始め、終わったころには残り20分ほどになっていた。
見直しをしていると、最後の「十分先で等差」の後処理ができていないことに気付く。慌てふためいていると試験が終了してしまい、せっかく全完チャンスだったのに～とかなり悔しい気持ちになった。
まあ、それまでの部分でかなり非自明なことをやっているし、全体で775くらいなのかなという体感だった。

試験が終わり、何人かと喋ったところ2完が多かった。明日2完すれば金もあるかな～などと皮算用をし、明日に向けて気持ちを切り替えた。

Day2

IMO2023day2

分野はACGだ！全完したいな～
4を見よう。(最初のコメントは特にない)
3034ってのは$\frac{3}{2}n$オーダーなのかな。となると強化帰納法になるのだろうか。
実験してみると何も考えず相加相乗するだけではオーダー感がぜんぜん足りないことが分かる。ということは帰納法のようにより低次の式を利用していきたいと考えるのが自然だろう。
気合で展開すると、$x_n$の周りだけ取り出して相加相乗をすると二段階で仮定が使えて、いけました！あまり迷走はしていないのだが50分ほどかかった気がする。

5番を見よう。面白そう。6番を見よう。5番の方がまだわかりそうだな。というかこれanti-pascal(IMO2018-P3のこと)？

「実験だーーー！！」(答案用紙より引用)

...実験がうまくいかない。こういうときは自明に上下から挟んでいくといい感じになることが分かっています

まずは上から。$n$は自明。$\frac{1}{2}n$くらいも構成できるな。
もうちょいうまく詰めようとすると三角数くらいで切り替わりそう...みたいな感じになった。これは実験結果と整合するけど、さすがに$\log_2$かなって感じ。ここまでは2022-春4と全く同じですね(苦い思い出)。
とまあここで無事$\log_2 n$くらいの構成ができて、あとは評価です。

「評価こそ構成の特徴をみつめよう」(by まいん)という信条に基づいて考えてみましょう。僕の構成は上から順に
$1,1,3,1,3,5,7,1,3,5,7,9,...$という感じでした
まあなんとなく上から$1,3,7,15,...$番目で切りたくなりますよねー！
んーーーー。
ところで今はずっと上から下に下る勢いで考えていたので、今度は下から上に上っていきましょう。すなわち、
各マスについて、そのマスから上に見たときにどのくらい赤丸を通るかを考えましょう。あ、終わりました。
やった！(残り45分)

6を見る。自明なことをやる。coaxicalな円たちについては重心座標が扱いやすいが試してみてもだめ。残りの見直しをする。とここでコンテストが終わってしまいました。

試験後

すっきり。気分が爽快です。なにより5が解けたことで成長を感じます。あとは嘘さえついてなければ満足ですね。

結果など

なんと777770の35点で金メダルでした。初参加で金なんて取っちゃっていいの？とは思いましたが何はともあれ金です。嬉しいです。
とはいうもののまだあまり受け入れることができていません。あまりのあっという間の出来事だったので。P3で7点が来たのも納得できていません。
これからゆっくりと時間を使って向き合っていきたいと思います。

未来の若者へ

嘘について

・嘘は徹底的に避ける
本番で嘘を避けなければならない理由は明確で、悔しいからです。解けないことよりも何よりも悔しい。
高一の間はあまり嘘をついたことがありませんでしたが、JMO22-1(C), JMO23-3(A), APMO23-3(G) で致命的な嘘をついてそれぞれ悲惨な感じになっていました。とりわけ春23の直前に複数の嘘が発覚したので、APMOから春までの5日間はどうやって嘘をなくせるかばかりを考えていました。
・不等号の向き
・非自明な同値性(いわゆる"言い換え")
・「さっきは何も得られなかったのにもう一回同じ式をいじってみたら有意な式が得られた」←とても嬉しい状況ですが、嘘の可能性が高いです。前の自分と少しでも食い違う状況があれば、もう一度慎重に検討しましょう。
・floorとかceilingまわり

自分がどの辺の嘘をつきやすいのかを知っていれば、見直しがスムーズになります。これを知るために場数を増やして日々の練習でたくさん嘘をついておくといいですね。

結果的に春の1(N)はしっかりと嘘をついてしまったのは悔しいものです。この問題は代表全員が7点を逃しています(4~6点に収まっています)。減点を味わってみたい人はぜひ取り組んでみましょう。

解答用紙の書き方について

僕の書き方はたぶん独特なものだと思います。刺さった部分があれば使ってみてください。
(とはいえ、本番のコンテストではちゃんとページ数は1から小さい順に連続する自然数を書きましょう。採点官が困ります)
P5の解答用紙1枚目
P5の解答用紙41.5枚目

僕は割と解答用紙を広く使います。というのも春合宿以降のコンテストは解答用紙・計算用紙が無制限に与えられるので、紙をケチる必要がありません。
なお予選・本選においては紙の枚数に制限がありますが、頑丈な消しゴムを持っていくことで実質的に無制限に使えます。僕はいつもこのテクニックを使って紙の枚数を増やしています。
おすすめの消しゴム

また、僕がやっていた方法として「思いついた方針を全て書き出す」というのがあります。上のIMOの箇所で実践を見せた通りです。
これをすると知ってる知識をフル活用することができるので有効です。特に一発ゲーが早く解けます。

以下に参考になる記事を載せておきます。
Evan Chenの記事

今まで解いた問題

僕は高2になってから今まで解いたSLPの問題をまとめるようになりました。
例えば EGMO はこんな感じ(←このリンクからスプレッドシートが見れます。)
EGMO

また SLP はこんな感じです
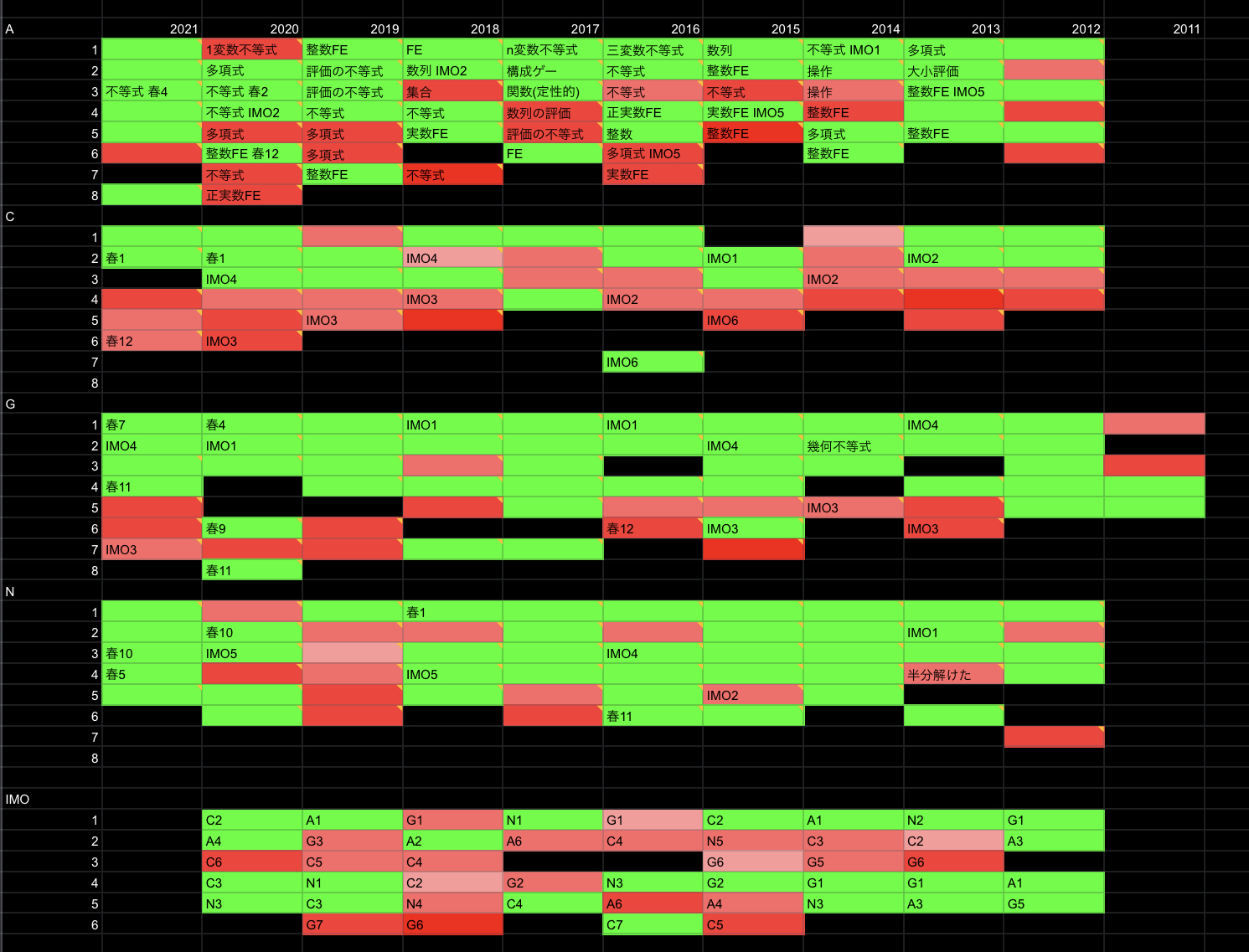SLP
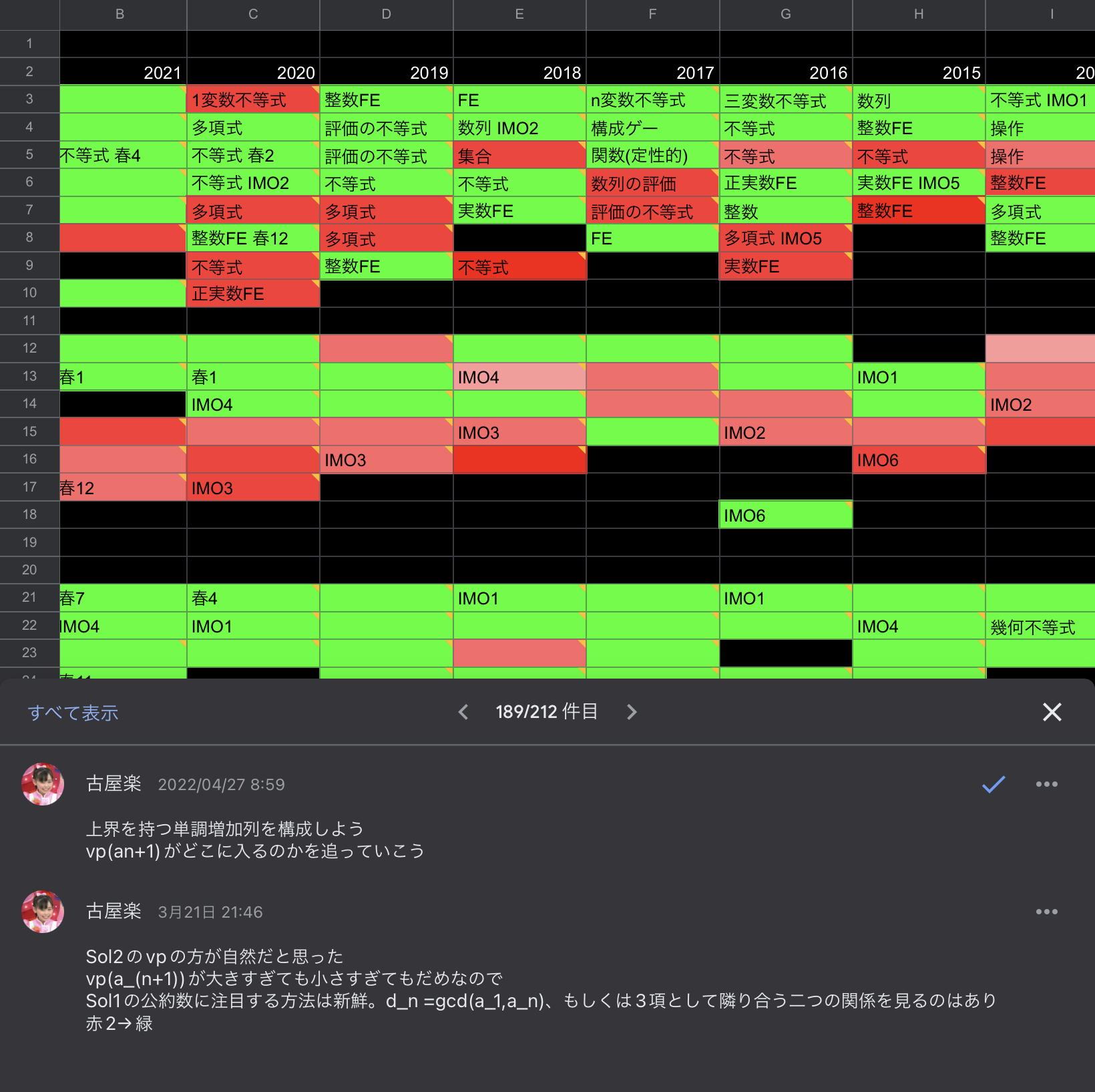コメント例

一つ一つの問題にコメントを付けています。

何をすればいいかわからないという人へ

この記事を読んで貰えばわかるであろう通り、僕は春合宿に行くまでは迷走していましたが、一度春合宿に行ってからは一本道の対策をやっていました。
ほとんどの人は春合宿に行ったことがないと思うのでその層に向けて話すとしたら、まずtwitterなどで仲間を作っておくというのは一つの手だと思います。今は OMC などの共通の話題もありますし、比較的容易に馴染めると思います。同年代で数オリに詳しい仲間がいればいろいろアドバイスがもらえますし、お互いにとって良い影響をもたらすはずです。
僕は今まで過去問を中心に取り組んできたので、あまりいろんなものをやらなきゃいけないと焦る必要はないと思います。やりたいものをやりましょう。それが一番です。

メッセージ

数オリファンの君へ。
春合宿やIMOなどの憧れの舞台を目指すなら、ひたむきに数オリをもっと愛しましょう。
問題、コンテスト、数オリ仲間、...愛すべき存在はたくさんあります。
現段階では、数オリ対策には確立されたメソッドがありません。
だからこそ、その好き度合いが結果に表れてきます。
がむしゃらにやっているその時間は決して無駄にはなりません。
もっと、もっと愛してください。
春合宿で会えるのを楽しみにしています！！！！！！！

おわりに

僕が競技数学を生活の中心に置いていた2年半の間、さまざまな人の支えがあってやってこれました。僕のこの環境には感謝してもしきれません。
今後は一数オリファンとして、そしてチューターとして未来の数オリファンを応援したいと思っています。
今までありがとうございました。