そこそこ美しい等式 atan(1)+atan(2)+atan(3)=π
そこそこ美しい等式
数学では様々美しい等式がある。時々思い出す等式について書く。
$\atan(1)+\atan(2)+\atan(3)=π$
という式が成り立つ。
ここで、$\atan$は$y=\tan \theta$の逆関数のある分枝で、$\theta = \atan (y) , 0 < \theta < \pi,とする。\atan \infty = \frac{\pi}{2} $とみなす。
また、
$\atan(1)+\atan(\frac{1}{2})+\atan(\frac{1}{3})=\frac{π}{2}$という式も成り立つ
図で説明すると、
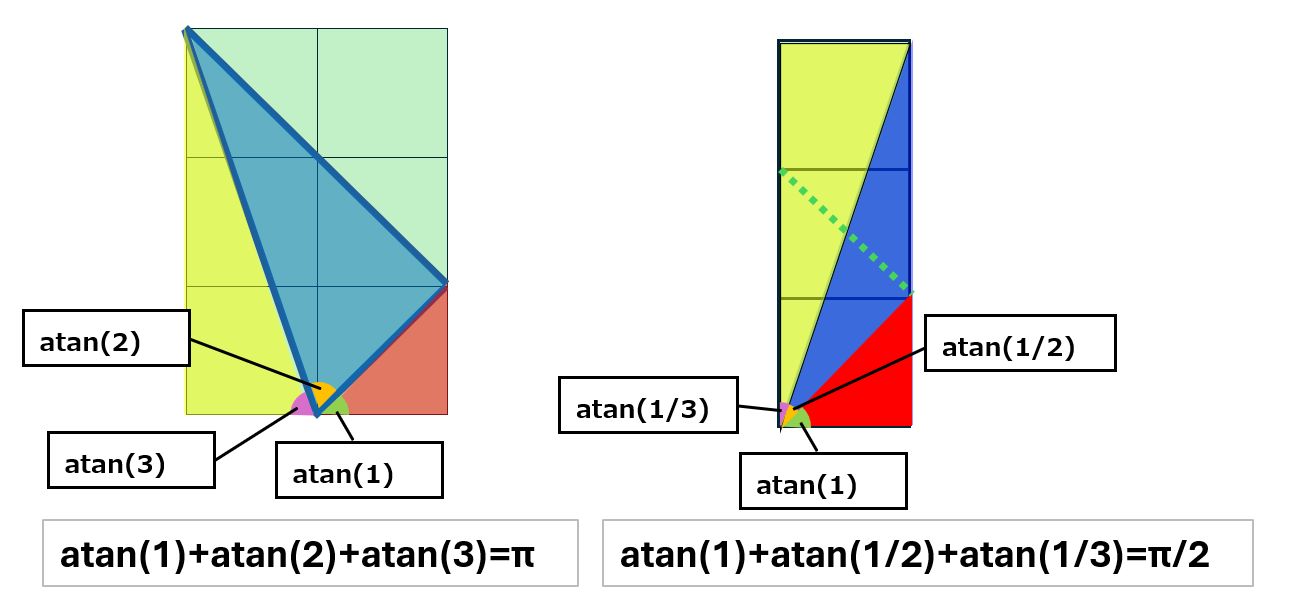atanの不思議
である。
ある一般化を考えてみた
$\atan(A)+\atan(B)+\atan(C)=\pi$や $\atan(A)+\atan(B)+\atan(C)=\frac{\pi}{2}$が成り立つような$A,B,C$を求める
| 図 | 説明 |
|---|---|
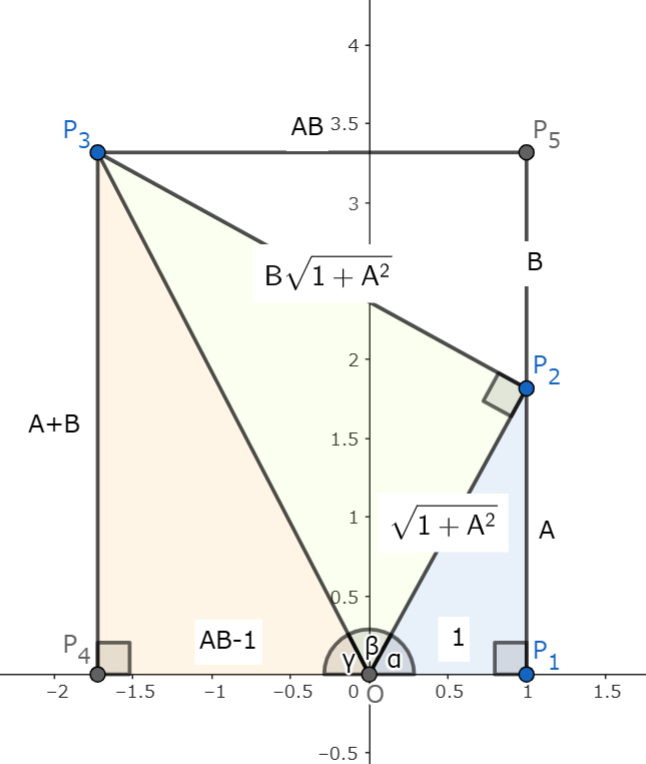α+β+γ=π
| 原点$O$の周りに角$\alpha, \gamma, \beta$があって、 $\alpha+ \gamma+ \beta=\pi$となっているとする。 $A=\tan \alpha,B=\tan \beta,C=\tan \gamma$とする 原点$O$と点$P_1(1,0)$を直角に接する一辺とする $\alpha$になる角を含む直角三角形$OP_1P_2 $について、 $P_1P_2=A$ なので斜辺は $OP_2=\sqrt{1+A^2}$ 直角三角形$OP_2P_3$を考えると、 $P_2P_3=B\sqrt{1+A^2}$ 直角三角形$P_2P_5P_3$は$OP_1P_2$と相似なので、 $P_2P_5=B$, $P_5P_3=AB$ 直角三角形$OP_4P_3$で $OP_4=AB-1$,$P_4P_3=A+B$ $\tan \gamma =\frac{A+B}{AB-1}$となるので$C=\frac{A+B}{AB-1}$となる。 |
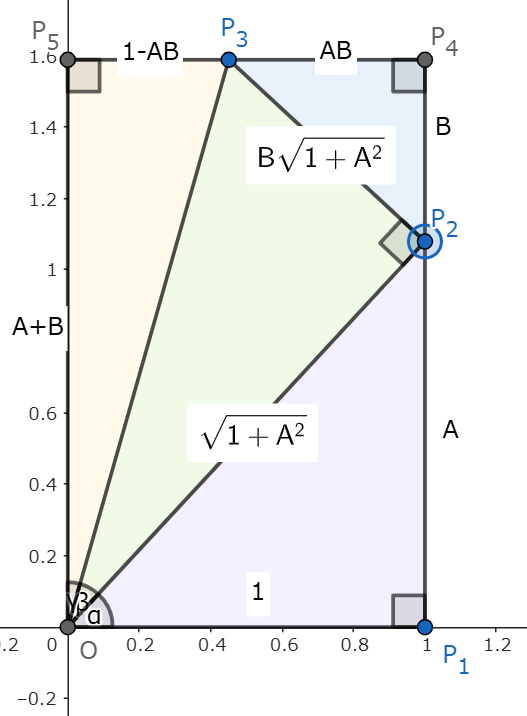α+β+γ=π/2
| 原点$O$の周りに角$\alpha, \gamma, \beta$があって、 $\alpha+ \gamma+ \beta=\frac{\pi}{2}$となっているとする。 $A=\tan \alpha,B=\tan \beta,C=\tan \gamma$とする 原点$O$と点$P_1(1,0)$を直角に接する一辺とする $\alpha$になる角を含む直角三角形$OP_1P_2 $について、 $P_1P_2=A$ なので斜辺は $OP_2=\sqrt{1+A^2}$ 直角三角形$OP_2P_3$を考えると、 $P_2P_3=B\sqrt{1+A^2}$ 直角三角形$P_2P_4P_3$は$OP_1P_2$と相似なので $P_2P_4=B$, $P_4P_3=AB$ $P_5P_3=1-AB$,$OP_5=A+B$ $\tan \gamma=\frac{1-AB}{A+B}$ $C=\frac{1-AB}{A+B}$となることがわかる。 |
（別の求め方）複素平面で考える
原点の周りの角度は、複素数の偏角に対応していることを利用する。
$Z=(1+Ai)(1+Bi)(1+Ci)$
$=(1-AB+(A+B)i)(1+Ci)$
$=(1-AB-BC-CA)+(A+B+C-ABC)i)$
- $\atan(A)+\atan(B)+\atan(C)=\pi$となるのは
$Z$が実数になるとき、つまり虚部が$0$になるときなので、
$A+B+C-ABC=0$
$C$について解くと$C=\frac{A+B}{AB-1} $である - $\atan(A)+\atan(B)+\atan(C)=\frac{\pi}{2}$となるのは
$Z$が純虚数になるとき、つまり実部が$0$になるときなので、
$1-AB-BC-CA=0$
$C$について解くと$C=\frac{1-AB}{A+B} $である
逆に$A,B,C=\frac{A+B}{AB-1}$であれば、$atan(A)+\atan(B)+\atan(C)=π$
$0< A<\pi ,0< B<\pi ,AB>1$とするとき
$\atan(A)+\atan(B)+\atan(\frac{A+B}{A B -1})=π$
$A=\tan \alpha, B=\tan \beta $とする。
以下の2つの事実を使う。
- $\tan (\alpha + \beta)=\frac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)}=\frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta }{\cos \alpha \cos \beta - \sin \alpha \sin \beta }=\frac{\tan \alpha + \tan \beta }{1 - \tan \alpha \tan \beta }$
（$\tan$の加法定理） - $0<\gamma<\pi$に対して
$\tan (\pi - \gamma) =\frac{\sin (\pi - \gamma)}{\cos (\pi - \gamma)} =\frac{\sin \gamma}{-\cos \gamma}=-\tan \gamma$
なので$\atan (-\tan \gamma)=\pi - \gamma$
$\atan(A)+\atan(B)+\atan(\frac{A+B}{A B -1})$
$=\alpha + \beta+\atan(\frac{A+B}{A B -1})$
$=\atan (\tan (\alpha + \beta))+\atan(\frac{A+B}{A B -1})$
$=\atan (\frac{\tan \alpha + \tan \beta }{1 - \tan \alpha \tan \beta })+\atan(\frac{A+B}{A B -1})$
$=\atan (\frac{A + B }{1 - A B})+\atan(\frac{A+B}{A B -1})$
$=\pi-\atan(\frac{A+B}{A B -1})+\atan(\frac{A+B}{A B -1})$
$=\pi$∎
図にすると、単位半円弧上の2点と原点を結ぶ直線と$x$軸がなす3つの角と2直線の傾き(各点からの隣の線分への各垂線の長さ)の関係である。
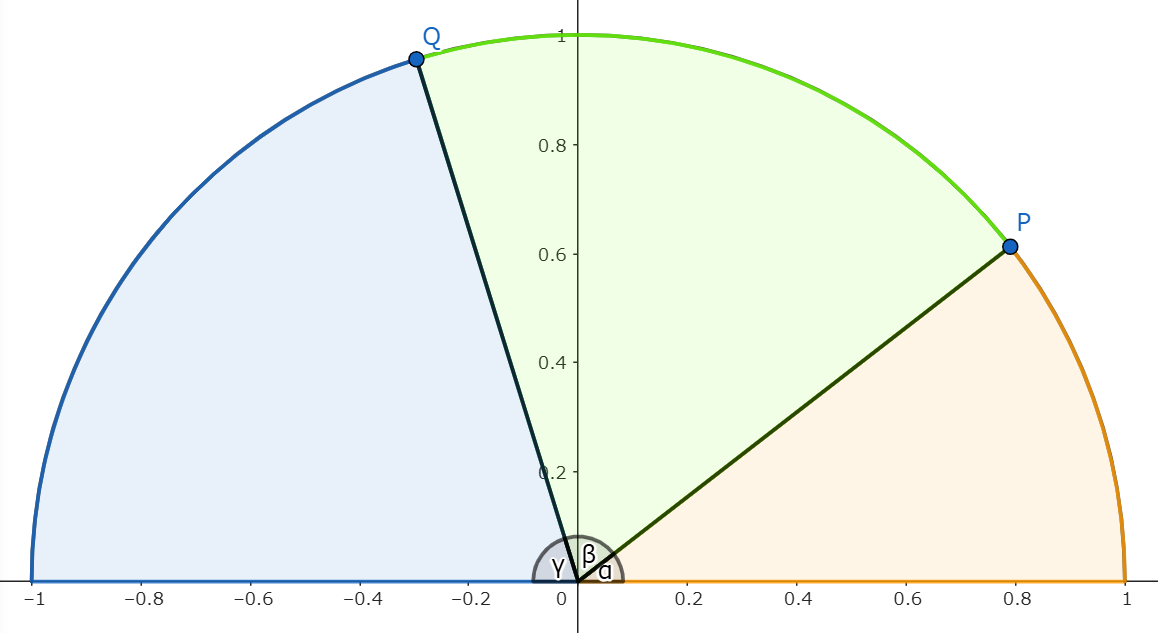半円上の2点と原点を結ぶ線とx軸のなす角度
逆に$A,B,C=\frac{1-AB}{A+B}$であれば、$atan(A)+\atan(B)+\atan(C)=π/2$
$\atan(A)+\atan(B)+\atan(\frac{1-A B}{A + B})=\frac{\pi}{2}$
$A=\tan \alpha, B=\tan \beta $とする。
- $0<\gamma<\frac{\pi}{2}$に対して
$\tan (\frac{\pi}{2} - \gamma) =\frac{\sin (\frac{\pi}{2} - \gamma)}{\cos (\frac{\pi}{2} - \gamma)} =\frac{\cos \gamma}{\sin \gamma}=\frac{1}{\tan \gamma} $
なので$\atan (\frac{1}{\tan \gamma})=\frac{\pi}{2} - \gamma$
を使う。
$\atan(A)+\atan(B)+\atan(\frac{1-A B}{A+B})$
$=\alpha + \beta+\atan(\frac{1-A B}{A+B})$
$=\atan (\tan (\alpha + \beta))+\atan(\frac{1-A B}{A+B})$
$=\atan (\frac{\tan \alpha + \tan \beta }{1 - \tan \alpha \tan \beta })+\atan(\frac{1-A B}{A+B})$
$=\atan (\frac{A + B }{1 - A B})+\atan(\frac{1-A B}{A+B})$
$=\frac{\pi}{2} - \atan(\frac{1-A B}{A+B})+\atan(\frac{1-A B}{A+B})$
$=\frac{\pi}{2}$∎
こちらも、図で描くと第一象限の四分円弧上の2点と原点を結ぶ直線と、$x$軸と$y$軸がなす3つの角と直線の傾き(各点からの隣の線分への各垂線の長さ)の関係である。
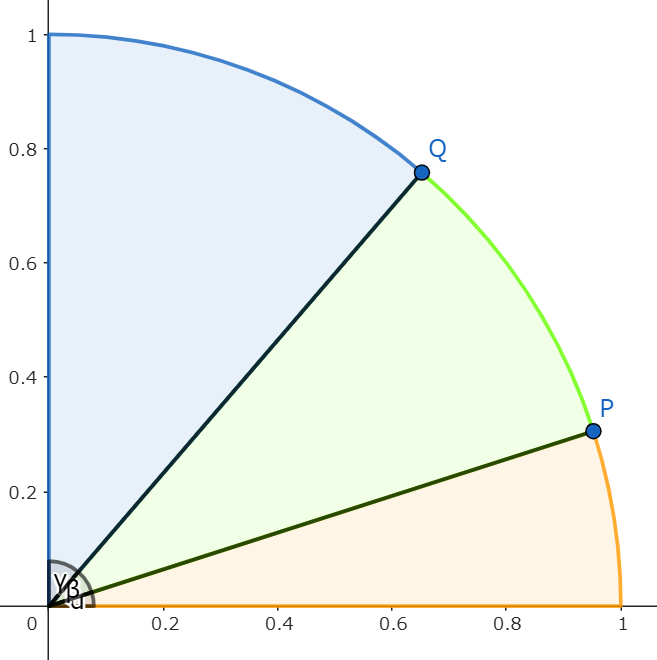四分円上の2点と原点を結ぶ線とx軸y軸のなす角度
3つの数$A,B,\frac{A+B}{A B -1}$について
半円弧の2点と原点を結ぶ直線の図でも明らかだが、
$C=\frac{A+B}{A B -1}$とすると、
$C(AB-1)=A+B$
$A(BC-1)=B+C$
$A=\frac{B+C}{B C -1}$
同様に
$B=\frac{C+A}{C A -1}$
となるので、1つが他の2の数の同様な対称式で表せる。
3つの数が対称的になっている。
実際、
$\atan(A)+\atan(B)+\atan(C)=π$
は左辺の和を並べ替えても変わらないことを考えても3つの数は対称的になっている。
3つの角を複素数の偏角として考えたときの積$(1+Ai)(1+Bi)(1+Ci)$の虚部が$0$の式
$A+B+C-ABC=0$
$A+B+C=ABC$
和と積が一致するというとても特徴的な対称性を持っている。
$A+B+C=ABC$を満たす、3つの異なる数$A,B,\frac{A+B}{A B -1}=C$がすべて正整数になるのは、これらの値が1,2,3の並べ替えだけである。
$ (A,B,C)=(1,2,3)\ or\ (1,3,2)\ or\ (2,1,3)\ or\ (2,3,1)\ or\ (3,1,2)\ or\ (3,2,1)$
$C=\frac{A+B}{AB-1}=\frac{A+B}{(A-1)(B-1)+(A+B)-2}$
$D:=(A-1)(B-1)-2$とする。
$C=\frac{A+B+D-D}{A+B+D}=1-\frac{D}{A+B+D}$
$A=1,B>3$の場合
$D=-2$
$C=1+\frac{2}{B-1}$なので$1< C<2$
$C$は整数ではない。$A>1,B>3$の場合
$D=(A-1)(B-1)-2 \geq 3-2=1>0$
$C=1-\frac{D}{A+B+D}<1$
$C$は整数ではない。
$A,B$を入れ替えてもこれまでの事が成り立つから、$A \leq 3,B \leq 3$である。
$A=1,B=2$の時、$C=\frac{3}{2-1}=3$
$A=1,B=3$の時、$C=\frac{4}{3-1}=2$
$A=2,B=3$の時、$C=\frac{5}{6-1}=1$
$C$の式で、$A,B$は対称的なので入れ替えても$C$は同じなので、$(A,B,C)$は、
$ (1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1)$のどれか∎
$\atan(1)+\atan(2)+\atan(3)=π$
を一般化して、
$\atan(A)+\atan(B)+\atan(C)=π$,$C=\frac{A+B}{A B -1}$
を考えたが、正整数という条件を付けると、結局並べ替えを除いて同じ式
$\atan(1)+\atan(2)+\atan(3)=π$
に戻ってきてしまい、この式の美しさが際立っていることが分かった。
では、
$\atan(1)+\atan(\frac{1}{2})+\atan(\frac{1}{3})=\frac{π}{2}$
に関しての一般化、
$atan(A)+\atan(B)+\atan(C)=\frac{π}{2}$,$C=\frac{1-A B}{A + B}$
についても同様に以下が成り立つ。
$\atan(\frac{1}{a})+\atan(\frac{1}{b})+\atan(\frac{1}{c})=\frac{π}{2}$
3つの異なる数$a,b,c$がすべて正整数になるのは、これらの値が1,2,3の並べ替えだけである。
$ (a,b,c)=(1,2,3)\ or\ (1,3,2)\ or\ (2,1,3)\ or\ (2,3,1)\ or\ (3,1,2)\ or\ (3,2,1)$
証明
$C=\frac{1-A B}{A + B}$
に$A=\frac{1}{a},B=\frac{1}{b},C=\frac{1}{c}$を代入すると、
$\frac{1}{c}=\frac{1-\frac{1}{a}\frac{1}{b}}{\frac{1}{a}+\frac{1}{b}}=\frac{ab-1}{b+a}$
$c=\frac{a+b}{ab-1}$
$a,b,c$は上で示したものと全く同じ形の3つ組になるので、条件を満たすものは1,2,3の並べ替えだけである。∎
$atan(A)+\atan(B)+\atan(C)=\frac{\pi}{2}$の方の式も、ある意味$atan(A)+\atan(B)+\atan(C)=\pi$の式と同じことだったのである。
別々の式$\atan(1)+\atan(2)+\atan(3)=π$と$\atan(1)+\atan(\frac{1}{2})+\atan(\frac{1}{3})=\frac{π}{2}$とがつながった。
そして、これらの美しい等式は「偶然」ではない背景を感じさせてくれる。
正整数に限れば、最初の$3$つの数だけが満たす関係式という意味でも美しかったことが分かった。
終わりに
逆正接に関する一見たまたま成り立つ美しいと思える関係式から初等的知識で考えるだけでも結構面白いと思える事実が分かった。何か更なる背景があるのかもしれない。有識者から見れば当たり前の事なのかもしれないが、一人遊び的にこれだけでも十分に楽しむことができた。数学は少ない知識でも結構遊ぶことができるのがとても素晴らしい。