奈良素敵大学模試(自作模試)大問4〜解説〜

問題

同一平面上に2つの円$C_1$と$C_2$があり、2円の半径はいずれも1で、2円の中心間距離は4である。円$C_1$上に動点$P$をおき、点$P$から円$C_2$に2本の接線$l_1,l_2$を引く。また、$l_1,l_2$と円$C_2$の接点をそれぞれ$Q,R$とする。点$P$が円$C_1$上を動くとき、
(1)線分$QR$が通過する領域$X$を図示せよ。
(2)領域$X$の面積$S$を求めよ。

まだ解いていない方はこちらから 記事 へ飛べます。答えを見たくない場合はどうぞ。

作問の意図

設定がシンプルで明快です。これは2つの茶碗の上で箸を滑らせていたときに思いつきました。(！！！)
初めは2円の距離$r$でやっていたのですが、逆三角関数が出てきてしまうので、有名角になるように$r=4$としてみましたが、問題に比べて答えはなかなか煩雑になってしまいました。
本番で出たなら間違いなく時間食い虫の大問でしょう……。
ただ、使う道具は多岐に渡るのでそこは気に入っていたりします。
では解説に移りましょう。

解説

(1)まず、座標に置く方針を取ることとする。(図示せよ、なので図形というより座標では？それに領域が円や$n$角形にはならそうだし……と勘づきたい)
$C_1:x^2+y^2=1,C_2:x^2+(y-4)^2=1,P(\cos t,\sin t)$とおき、$C_1,C_2$の中心をそれぞれ$O(0,0),O'(0,4)$とおく。
$O'P^2=\cos^2 t+(4-\sin t)^2$であるから三平方の定理より、
$PQ=\sqrt{O'P^2-1}=2\sqrt{4-2\sin t}$だから、中心を$P$、半径を$PQ$とする円$C_3$は
$(x-\cos t)^2+(y-\sin t)^2=8(2-\sin t)$と表される。
直線$QR$の方程式は$C_2,C_3$の差をとって、$(4-y)\sin t-x\cos t=15-4y$
合成を行って、$\sqrt{(y-4)^2+x^2}\sin(t-\alpha)=15-4y \ (\sin\alpha=\frac{x}{\sqrt{(y-4)^2+x^2}})$
$-1\leq \sin(t-\alpha)\leq 1$かつ$(y-4)^2+x^2\geq 0$より$-\sqrt{(y-4)^2+x^2}\leq 15-4y\leq \sqrt{(y-4)^2+x^2}$
場合分けする。
(i)$15-4y\geq 0$のとき、左辺と中辺の大小関係は常に成り立つ。
中辺と右辺の両辺を2乗して(両辺正なので同値のまま)
$x^2-15y^2+112y-209\geq0$
(ii)$15-4y< 0$のとき、中辺と右辺の大小関係は常に成り立つ。
左辺と中辺の両辺を2乗して(両辺負なので反転させれば同値のまま)
$x^2-15y^2+112y-209\geq0$
ゆえに領域は$x^2-15y^2+112y-209\geq0,x^2+(y-4)^2\leq1$
境界線を描くと次のようになる
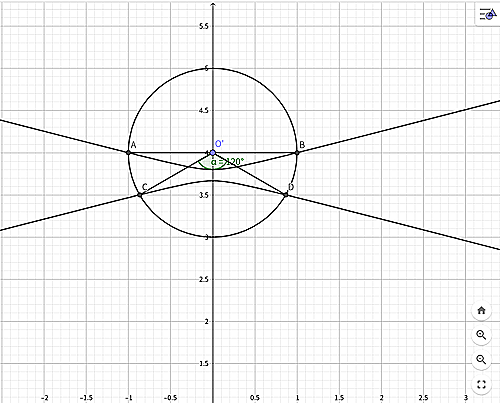図示した結果(境界のみ)

(2)$y$軸方向に積分する。$x^2-15y^2+112y-209=0$と$y$軸の交点を求めると、$\displaystyle(0,\frac{11}{3}),(0,\frac{19}{5})$より、
$S=\displaystyle\frac{\pi}{2}-(T+T'+U),T=2\displaystyle\int_{\frac{19}{5}}^{4}\sqrt{15y^2-112y+209}dy,T'=2\int_{\frac{7}{2}}^{\frac{11}{3}}\sqrt{15y^2-112y+209}dy,U=\frac{\pi}{3}-\frac{\sqrt{3}}{4}$
となる。まず$\displaystyle\int\sqrt{15y^2-112y+209}dy=\int\sqrt{15\left(y-\frac{56}{15}\right)^2-\frac{1}{15}}dy$を計算する。
$\displaystyle u=15\left(y-\frac{56}{15}\right)$と置換すれば、$\displaystyle\frac{du}{dy}=15$より、
$\displaystyle\frac{1}{15\sqrt{15}}\int\sqrt{u^2-1}du=\frac{1}{30\sqrt{15}}\left(u\sqrt{u^2-1}-\log|u+\sqrt{u^2-1}|\right)+C$($C$は積分定数)
したがって、おのおの区間を$\displaystyle u=15\left(y-\frac{56}{15}\right)$と置換することにより、
$T=\displaystyle\frac{1}{15\sqrt{15}}\left[u\sqrt{u^2-1}-\log|u+\sqrt{u^2-1}|\right]_1^4=\frac{4}{15}-\frac{1}{15\sqrt{15}}\log(4+\sqrt{15})$
$T'=\displaystyle\frac{1}{15\sqrt{15}}\left[u\sqrt{u^2-1}-\log|u+\sqrt{u^2-1}|\right]_{-\frac{7}{2}}^{-1}=\frac{7}{20\sqrt{3}}+\frac{1}{15\sqrt{15}}\log\left(\frac{7-3\sqrt{5}}{2}\right)$
ゆえに整理して$\displaystyle S=\frac{\sqrt{15}}{225}\log{\frac{8+2\sqrt{15}}{7−3\sqrt{5}}}+\frac{π}{6}+\frac{2}{15}(\sqrt{3}−2)$である。

はい。お疲れさまでした。

これ以外に別解などあればぜひコメントください。指摘も歓迎です。