エックマン-ヒルトンの定理の視覚的証明が面白い
最近面白いと感じた証明
今回は完全にWikipediaの記事にあることの受け売り(紹介)です。
数学のWikipediaをいろいろ辿っていて、面白いと感じたことの紹介になります。
素人ですので間違いがあるかもしれませんので、鵜吞みにはしないでください。また問題個所があればご指摘お願いいたします。
この記事を書いたキッカケはWikipediaの記事で難しい話題中に、予備知識不要で数行で「証明」が終わる命題を見つけたからです。
それが登場したWikipediaのページとして、$2$次以上のホモトピー群の可換性のところにリンクがあって、それを眺めてみたら実に「算数」的に証明を追えるものだ!一目でわかる!と思ったからで、あまり話題になってるのを見たことなかったので、一般世間の数学ファンに「そういうものがあるんだ!」というのが広まってほしいと思ったからです。難しい話題の中に出てくる命題だけど実は証明を追うのは簡単という「体験」を共有したかったのです。
この記事の本題はエックマン-ヒルトンの定理なので、その見出しまでは読み飛ばしていただいて構いません。
ホモトピー群
位相幾何学で、「
ホモトピー群 - Wikipedia
」という、2つの図形(位相空間)に対してそれぞれそれから定まる群を対応させて、その群が同型でないことを示して、元の図形と図形が同相でないことを示すことができたりする
不変量
概念があります。
n次元ホモトピー群は、n次元球面から図形への写像をもとに定義されます。詳細はWikipediaをご参照ください。
基本群
特に1次元ホモトピー群は「
基本群 - Wikipedia
」と呼ばれてるもので、ある点からロープを図形内にはわせてもとの点に戻ってくるように置いた時に、空間のどこかに引っかからないように動かせる置き方は同じ置き方だとして分類して本質的に異なる物を要素とした(ロープの置き方)の集合にその要素のロープを連結することを演算として入れたもので、群になります。
NHKのポアンカレ予想に関するNHKスペシャルや
笑わない数学のポアンカレ予想回
等で「回収できるロープ」と言っていたのは、ロープが図形内の円板の境界に配置されている場合など図形内を通ってロープを始点に回収できてしまうもので、基本群の単位元に当たるものです。逆元は逆向きのロープになります。1点からどの点を終点としてロープを置くことができて、このロープの動かしたものしかありえない(回収できる置き方しかない)図形(空間)を
単連結
といいます。
円周の基本群
例えば、円周の基本群は$\mathbb{Z}$(整数全体)になります(厳密な証明は大変長い)。直観的には、円周上のある始点から1回左回り1周するロープを置くのが+1で1回右回りに1周するロープを置くのが-1に対応して、円周にロープを1回左回りに置いた1周するロープにつなげて右回りに置いたロープを始点から引っ張ると最終的には回収できる(0に対応)のがイメージできると思います。
円周の基本群はロープを繋げる演算が結局整数の足し算なので、可換になります。
8の字図形の基本群は非アーベル群
ところが、8の字図形(文字の8を図形と考えたもの、2つの円周が1点でくっついた形)では、上下の2つの円周を通る順番が異なるロープの置き方(上→下と下→上)は互いに図形内の移動で移りあわないため可換ではありません。
生成元が2個の「
自由群 - Wikipedia
」 と呼ばれるものになります。群の公理のみの関係式(単位元になる非自明な式)しかない群。$x 1=1 x=x $,$x^{-1}x=xx^{-1}=1$などしか関係式を持たない群。
自由群は「
Free monoid(自由モノイド) - Wikipedia
」において、各元の逆元を形式的に考えて導入したものです。
自由モノイドは、$n$種類の文字をつかった文字列の集合に文字列の連結で演算を入れたものです。単位元は空文字列。
$n=1$の時は1種類の文字なので、例えば文字の種類集合$\{a\}$として
$aa+aaa=aaaaa=aaa+aa$
となり可換となります。(結局、文字列の長さという非負自然数を考えていることと同じ)
$n>1$の場合例えば$n=2$の時、文字の種類集合$\{a,b\}$として
$a+b=ab\neq ba=b+a$
なので可換ではありません。
この自由モノイドの各元xに逆元$x^{-1}$が「ある」と考えたものが自由群なので、
$n=1$の時は円周の基本群で整数全体と同じものになり($a$の数-$a^{-1}$の数が整数に対応している)、
$n=2$の時は8の字の基本群の生成元が2つの自由群になるわけです。
円周と8の字は一般に「
ブーケ (花束) - Wikipedia
」と呼ばれる図形のそれぞれ、1弁、2弁の場合です。n弁のブーケの基本群は、生成元がn個の自由群となります。
8の字のように比較的簡単な図形でも2元生成の自由群といった非アーベル群(非可換群)となってしまうのです。
n次元ホモトピー群(n>1)はアーベル群(可換)
名前に基本とついている基本群(1次元ホモトピー群)には、非アーベル群となる場合がある、というかむしろ単連結な図形とか円周とかトーラス(複数の円周の直積)のような図形はアーベル群ですが、それ以外は非アーベル群になってしまいます。
ところが、意外なことに$n \geq 2$のn次元ホモトピー群は全てアーベル群(可換群)になってしまいます。
エックマン-ヒルトンの定理
歴史的には、高次のホモトピー群が定義されてすぐに、直接的にアーベル群だと証明されたそうです。後になって、もっと一般的な代数系の定理を使えば導けるとわかったようです。その定理が次の エックマン-ヒルトンの定理(論法) です。論文でこの論法を最初に使用した2人の数学者 エックマン と数学者 ヒルトン の名前が付けられたようです。初等数学(算数)的に証明を追えます。
ある集合$M$に2つの二項演算
$◇,◆:M \times M \longrightarrow M $
があり、それぞれの演算に単位元
$1_◇、1_◆$があり ($a◇1_◇=1_◇◇a=a、a◆1_◆=1_◆◆ a=a$)、
任意の元$a,b,c,d \in M$に対して、等式
$(a◇b)◆(c◇d)=(a◆c)◇(b◆d)$
を満たすならば、以下が成り立つ。($M$は可換モノイドになる)
- 2の演算の単位元は同一$\quad 1_◇=1_◆$
- これらの演算は同一$\quad (a◇b)=(a◆b)$
- (これらの)演算は可換である$\quad (a◇b)=(b◇a)$
- (これらの)演算は結合律を満たす$\quad (a◇(b◇c))=((a◇b)◇c)$
3.可換律や4.結合律は仮定してないのに仮定から自動的に成り立つことがわかるのがとても面白いと思います。
ある集合$S$と、その元の$a,b$に対して、二項演算$・$があって、
- (閉じている)演算結果がまた$S$の元になる: $a・b \in S$
- (結合律)$ \forall a,b,c \in S ; a・(b・c)=(a・b)・c$
- (単位元の存在)$ \exists e \in S, a \in S ; a・e=e・a=a$
- (逆元の存在)$e$を単位元として、$ \forall a \in S, \exists a'\in S;a・a'=a'・a = e $
- (可換性)$ \forall a,b \in S; a・b=b・a$
[1]を満たす$S$と演算の組をマグマという
[1][2]を満たす$S$と演算の組を半群という
[1][2][3]を満たす$S$と演算の組をモノイドという
[1][2][3][4]を満たす$S$と演算の組を群という
[5]を満たすものを可換〇〇という。〇〇には上記の代数系が入る
例:可換モノイド、可換群
また、可換群の事をアーベル群ともいう
つまりアーベル群とは[1]-[5]まですべて満たす代数系である
エックマン-ヒルトンの定理(論法)は、一つの集合$M$で2つの演算があり、
そのそれぞれで[1]閉じていることと[3]単位元の存在と、
$(a◇b)◆(c◇d)=(a◆c)◇(b◆d)$
を仮定するだけで、
[2]結合律と[5]可換性が導かれてしまうという事です。
エックマン-ヒルトンの定理(論法)を言い換えると
$M$が演算$◇,◆$で単位的
マグマ
をなしていて、等式
$(a◇b)◆(c◇d)=(a◆c)◇(b◆d)$
が成り立つならばこれらの演算$◇,◆$は同一で$M$は(その演算で)可換モノイド
定理の単位マグマとなっているところは、モノイド(結合律が最初から成り立つ)に変えてももちろん成り立ちます。さらに群に置き換えると、結論はアーベル群になります。(群は逆元が存在するモノイドです。逆元の存在はこの定理の証明には不要です。)
$M$が演算$◇,◆$でモノイドをなしていて、等式
$(a◇b)◆(c◇d)=(a◆c)◇(b◆d)$
が成り立つならばこれらの演算$◇,◆$は同一で$M$は(その演算で)可換モノイド
$G$が演算$◇,◆$で群をなしていて、等式
$(a◇b)◆(c◇d)=(a◆c)◇(b◆d)$
が成り立つならばこれらの演算$◇,◆$は同一で$G$は(その演算で)アーベル群
定理の証明は以下のWikipediaページ
[Link]「
Eckmann–Hilton argument - Wikipedia
」
にわかりやすい証明が載っていますが、改めてこちらにも書きます。(受け売り)
仮定の等式が不自然ではないことも以下に書きます。
表し方と定理の仮定
2つの要素a,bに対して、a◇bは横につなげることで表す(水平結合)
2つの要素a,bに対して、a◆bは縦につなげることと表す(垂直結合)
 2つの演算
2つの演算
◇での単位元$1_◇$をeと書き、◆での単位元$1_◆$をfと書くことにすると、$a◇e=e◇a=a、a◆f=f◆a=a$
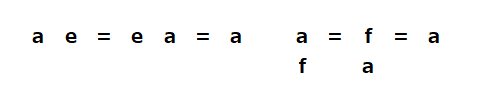 単位元e,f
単位元e,f
仮定の等式$(a◇b)◆(c◇d)=(a◆c)◇(b◆d)$ の
左辺は下図の上段の式で、水平結合したもの2つを垂直結合したものになり、
右辺は下図の中段の式で、垂直結合したもの2つを水平結合したものになり、
括弧を消すと$2 \times 2$行列風の同じ並びになっているので、等しいとみなす事は自然な仮定であることがわかる。
これらは同じものなので、以降は下段の$2 \times 2$行列風の並びで表す。
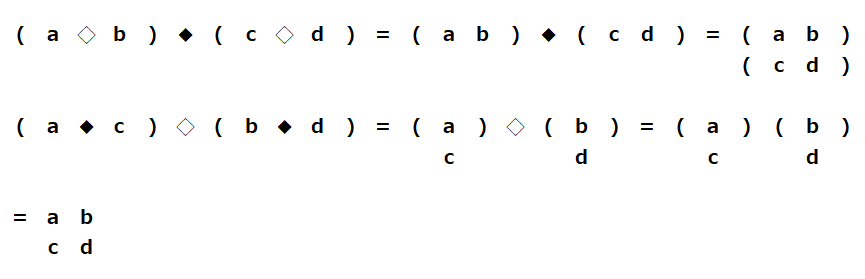 水平結合→垂直結合と垂直結合→水平結合
水平結合→垂直結合と垂直結合→水平結合
ここまでが定理の仮定である。これらを使用すると、以下が導かれる。
導かれること
1. 2つの演算の単位元が同じ元である
 単位元の同一性
単位元の同一性
| 式で証明 |
|---|
| $f=f◆f=(f◇e)◆(e◇f)=(f◆e)◇(e◆f)=e◇e=e$ |
2つの演算の単位元が等しいこと(e=f)がわかる
2. これらの演算は同一
3. 演算の可換性
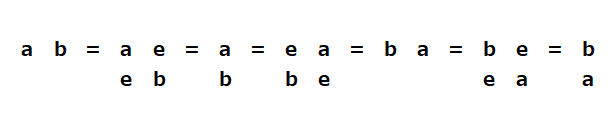 演算の同一性と可換性
演算の同一性と可換性
| 式で証明 |
|---|
| a◇b =(a◆e)◇(e◆b)=(a◇e)◆(e◇b) =a◆b =(e◇a)◆(b◇e)=(e◆b)◇(a◆e) =b◇a =(b◆e)◇(e◆a)=(b◇e)◆(e◇a) =b◆a |
水平合成◇と垂直合成◆は同じ演算で、可換(交換法則が成立、2項の順序を変えても等しい)がわかる
4. 演算の結合性
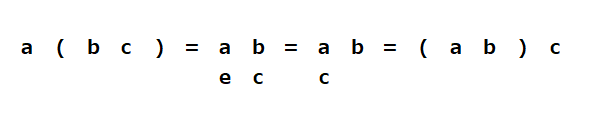 演算の結合性
演算の結合性
結合律も自動的に満たされてしまう事がわかる。
| 式で証明 |
|---|
| a◇(b◇c) =(a◆e)◇(b◆c) =(a◇b)◆(e◇c) =(a◇b)◆c =(a◇b)◇c |
よって結局◇と◆は同一の演算で可換で結合律を満たす。∎
図で視覚的に表したものでの証明の方が式よりも直観的にわかりやすいと感じました。$a◇b=a◆b=b◇a=b◆a $の図ではあたかも回転するようにして、可換性が証明されます。
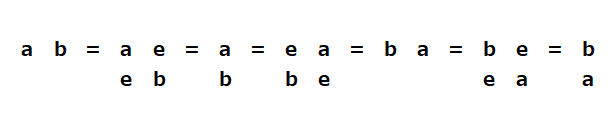 可換性(再掲)
可換性(再掲)
この議論が$n \geq 2$のn次元ホモトピー群が可換であることの証明に使用できるようです。
$n \geq 2 $の$n$次元ホモトピー群において、
各類の写像の定義域の$n$次元球面上の第1座標方向での結合を◇(水平結合)、
各類の写像の定義域の$n$次元球面上の第2座標方向での結合を◆(垂直結合)、
基点への定値写像の類を単位元としたとき、$n \geq 2 $なので第1座標と第2座標を入れ替える$n$次元球面の回転(これは可換性を示した図がそのまま類の結合演算に対応するイメージ)が存在するので、
$(a◇b)◆(c◇d)=(a◆c)◇(b◆d)$
が成立し、系によりアーベル群となる。
まとめ
集合$M$に閉じた二項演算が2つ($◇,◆:M \times M \longrightarrow M $)があり、以下の等式
$(a◇b)◆(c◇d)=(a◆c)◇(b◆d)$
が成り立つという仮定から、演算が同一で$M$はこの演算でモノイドになることがわかりました。
◇を水平結合、◆を垂直結合で図で表すと、仮定の等式は以下のように水平結合→垂直結合、垂直結合→水平結合の順によらない並びの行列と考えると自然な仮定であるとわかり、
 表し方と仮定
表し方と仮定
その行列を経由して、単位元の同一性、演算の同一性、可換性、結合性が自動的に導かれてしまう事を確認しました。この部分を図でまとめると以下のようになります。
 単位元と演算の同一性、可換性、結合性が導かれる
単位元と演算の同一性、可換性、結合性が導かれる
終わりに
数学は、面白い様々な概念や命題がありますが、難しい議論の果てにあったりするので、なかなかたどり着くことができません。実は面白い概念や命題は簡単でだれにも理解可能なものも潜んでいたりします。今回の命題も実は簡単な事実ですがあまり有名ではない非自明で話題にのぼりにくいものと感じました。そして、地道に参考書を最初から1方向に読んでいたらなかなかたどり着きにくい面白い話題の例だと感じました。その点、Wikipediaはリンクで1方向ではない辿り方ができるものです。ただし間違いや捏造もまぎれている可能性もあるので、鵜呑みにはせず慎重になる必要はありますが、数学の事実の場合は、自分で証明を追えば真偽が検証できる可能性もあるので、こういう数学の楽しみ方もアリだなと感じました。