気ままな物理の小文（１）フェルマーの原理：光学の中に潜む最適化問題

はじめに

この原稿は大昔、私がまだ大学院生だったときに書いた連載原稿の第一弾です。第７弾まではあって、探せば第１２弾まであるかもしれません。以前からきれいに書き直したいと思っていましたが、Mathlogがちょうどいい置き場なのかなと思い、アップする次第です。

まずは第一回は光の性質に関するフェルマーの原理を取り上げています。若干、お恥ずかしいところもありますが、ちょっと背伸びしたい高校生にちょうどいいかな、と思います。楽しんでいただければ幸いです。

なお、物理の法則や原理が「定理」という括りででてくるのは、ご愛嬌。いい見出しがなかったためなので、お見逃しください。

いろいろな最小化問題

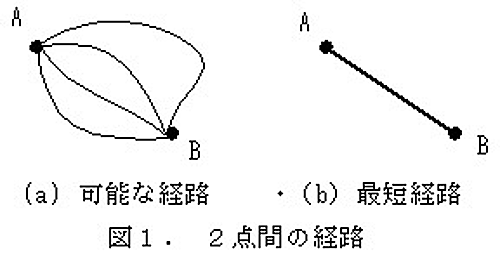fig1-1

まず、簡単な最小化問題から図1のように2点A, Bをとります。AからBに至る経路はいろいろ考えられますが、では「2点を結ぶ最短経路」はどうなるでしょうか。

答えは当然、ABを結ぶ線分ですね。

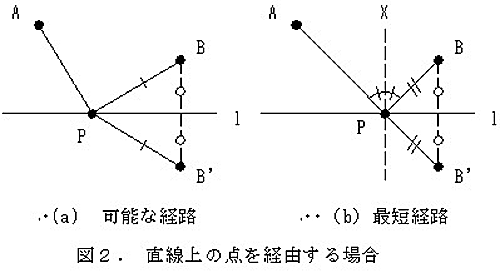fig1-2

では次。図2のように2点A, Bと直線をとります。直線$l$上に点Pをとって、折れ線APBを作ります。折れ線APBの長さを最小にするには、点Pをどこのとったらいいでしょうか。これも答えは簡単ですよね。点Bを直線$l$に対して対称移動した点B'をとります。PB=PB'ですから、折れ線APBを最小にするかわりに折れ線APB'を最小にすればよい。結局A, P, B'が一直線に並んだ時が、最短経路になります。この時、直線$l$に垂直な直線をPXとすれば、$\angle {\rm APX}=\angle {\rm BPX}$が明らかに成立します。

これらの2つの最小化問題は、数学の問題として解くことができるわけですが、実はとても深く関連した現象があります。

それは「光」です。

まず2点A, Bを通る光の経路を考えてみましょう。2点A, Bを通る光の経路は頭の中ではいろいろと考えることが出来ます。しかし実際に観測される光の経路は、ABを結ぶ直線となります(光の直進性)。これは始めに考えた問題(図1)と関連がありそうです。

次に点Aから出発し、鏡$l$上の点Pを経由して、点Bに到達する光を考えてみましょう。ここでもやはり光の経路を頭の中ではいろいろと想像することができ、それに応じて反射する点Pの位置もいろいろと考えられますが、実際に観測される点Ｐの位置はただ一つです。つまりPXを$l$に垂直な直線として、$\angle {\rm APX}$(入射角)$=\angle {\rm BPX}$(反射角)が成り立つような点Pで光は反射されるはずです。この光の性質のことを「反射の法則」と呼びますが、そんな法則を聞いたことがなくても、この性質は有名ですよね。これは先ほど考えた2番目の問題(図2)の答と一致していますね。

このように考えていくと、この光の２つの性質(直進性および反射の法則)は次の1つの原理にまとめることが出来そうです。

この原理はとても面白い。仮にこの原理を信じることにすると、光はまず伝搬する前に可能な経路をすべて試してみて、(中にはとんでもなく通回りな経路もあるだろうに)その中でもっとも最短な経路を見つけて、実際に通る道を決定していることになります。実際に光がそんなことをしているのかどうなのかは議論の余地がありますが、結果としてこんな変わった考え方で現象が説明できてしまうのです。

フェルマーの原理

さて、先に述べた原理を使って光の性質のすべてを説明できるでしょうか？残念ながら、そんなにうまくことは運びません。すぐに反例を見つけることが出来ます。皆さんは、プールサイドから見たプールの底の深さよりも、実際のプールの深さが深くて驚いたという経験はありませんか? この現象は次のように説明できます。プールの底から出た光は、図3のように水と空気の境界面で折れ曲がってしまいます。そのためにプールサイドから見たみかけ上の底の深さは、本当の深さより浅く見えてしまうのです。このように2つの異なる物質の境界面で光の進行方向が変わってしまう現象のことを、「光の屈折」といいます。この現象は先に述べた「原理？」では説明できません。もし光が最短経路を進むとするならば、光の経路が折れ線になることはないはずですから。

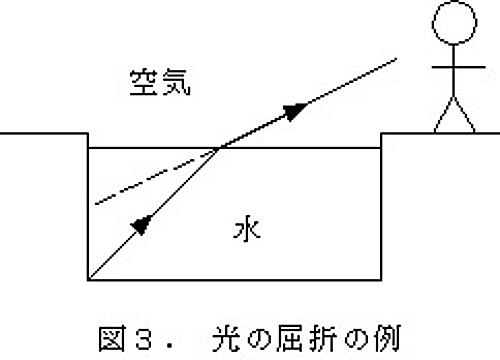fig1-3

では、この現象を一体どのようにして説明すれば良いでしょう？少なくとも最短経路ではだめです。この問題に答を与えたのが、１７世紀の物理学者フェルマーです。彼は次のように考えました。

先ほど述べた原理(?)と決定的に違うのは、最短経路というのをやめて最短時間としたことです。これによって、屈折の法則を次のように説明することが出来ます。図4を見て下さい。領域1と領域2はことなる物質によってできており、境界面Pによって隔てられているとします。プールの例では、領域1が空気で、領域2が水にあたっています。一般に物質中を通り抜ける時の光の速さは物質の種類によって異なります。ここでは領域1での光の速さの方が速いと仮定しましょう。（図3の例でいうと、空気中での光の速さの方が、水中での光の速さより速い、とするわけです。）領域1内の点Ａから出発して、境界面を通り、領域2内の点Bに到達する光を考えてみましょう。2点A, Bを通る光の経路は、頭の中ではいろいろ考えることが出来ます。では、最短時間でAからBに到達するような光の経路はどうなるでしょうか?

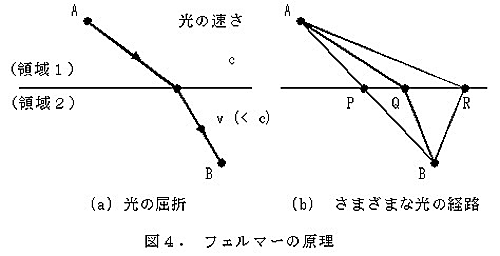fig1-4

この問題は、次のように例えることもできます。「領域1は舗装道路、領域2は荒れ地である。舗装道路では人は速く走ることができるが、荒れ地では速くは走れない。点Aから点Bまで人が最短時間で走るにはどういう経路でいけばよいか。」良く考えてみるとわかるように、この問題では、最短経路、すなわちABを結ぶ線分が答えにはなりません。図4に最短経路APBが描いてあります。しかし領域1の方が速く進めるので、できるだけ長く領域1内を進んだ方が、より早く点Bに到達できます。言い替えると、できるだけ長く「舗装道路」を進んだ方がいいのです。ですから、折れ線AQBのように進んだ方が、より短い時間でBに行けます。折れ曲がっている分、経路の長さは長くなりますが、領域1を長い時間進んでいるので、全体としてかかる時間は短くなります。しかし、領域1を進む時間をあまりに長くしまうと、今度は本当に遠回りになってしまいます。図4の折れ線ARBがその例です。そうして考えていくと、どこかに最短時間でＡからＢに到達する経路が存在しそうです。フェルマーの原理は、まさしくその最短時間で行けるような経路が実際に観測される光の経路であると、主張しているのです。

このようにフェルマーの原理を信じると、光の経路は自然と折れ線になります。また光が折れ曲がるのは、物質の種類によって光の速さが異なることが原因になっているのがわかるでしょう。また光の折れ曲がり方から、どちらの物質の方が光の速さが速いかもわかります。プールの例でしたら、水の中での光の速さは、空気中での光の速さに比べて、遅いことになります。実際に光の速さを測らずに、光の速さの大小関係が議論できてしまいました。

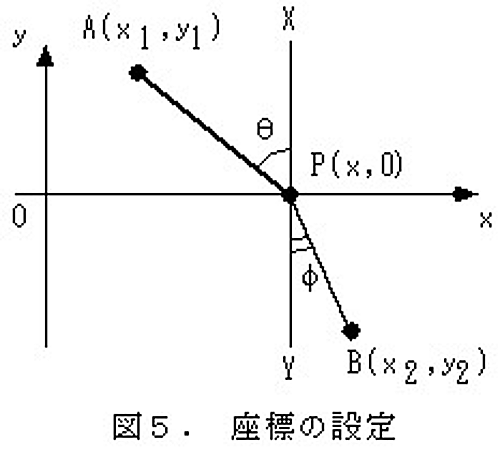fig1-5

今度は数式を使ってちゃんと考えてみましょう。領域1, 2での光の速さをそれぞれ$c$, $v$とおきます。図5のように境界面に沿って$x$軸をおき、点A, Bの座標を$(x_1,y_1)$, $(x_2,y_2)$とそれぞれおきます。$x$軸上に点Pをとって、折れ線APBを作ります。点Pの座標を${\rm P}(x,0)$とおいて、経路APBを光が進むにかかる時間$T$を計算してみると、

$\displaystyle{T=\frac{{\rm AP}}{c} + \frac{\rm BP}{v}=\frac{\sqrt{(x-x_1)^2+y^2}}{c} + \frac{\sqrt{(x-x_2)^2+y^2}}{v}}$

となります。これを最小にするように、$x$の値を決めればよいのですが、それには$T$を$x$で微分して0とおけばよい:

$\displaystyle{ \frac{dT}{dx} = \frac{x-x_1}{c\sqrt{(x-x_1)^2+y^2}}+ \frac{x-x_2}{v\sqrt{(x-x_2)^2+y^2}} = \frac{x-x_1}{c \cdot {\rm AP}} + \frac{x-x_2}{v \cdot {\rm BP}} = 0}$

ここで点Pにたてた垂線をPXYとおき、$\angle {\rm APX}=\theta$, $\angle {\rm BPY}=\varphi$とおくことにします（$\theta$: 入射角, $\varphi$: 屈折角）。ここで$\sin \theta=(x-x_1)/{\rm AP}$, $\sin \varphi =(x_2-x)/{\rm BP}$に注意すると、先ほどの式は、

$\displaystyle{ \frac{dT}{dx} = \frac{\sin \theta}{c} - \frac{\sin \varphi}{v} = 0}$

と変形され、最終的に入射角と屈折角の間には、

$\displaystyle{ \frac{\sin \theta}{\sin \varphi} = \frac{c}{v} = {\rm 定数}}$

なる関係式が成り立つことがわかります。この式は「スネルの法則」として、実験でよく確かめられています。こうしてフェルマーの原理は、全く異なる形をしたスネルの法則と等価であることが示せました。これほど違う形をしているのに、全く同じ主張なのです！ついでに、スネルの公式の右辺を$c/v=n$とおいたとき、$n$を屈折率といいますが、これは領域1と領域2の光の速度の比になっています。これもフェルマーの原理からの帰結です。

一般相対性理論への道

こうして、光の性質（光の直進性、反射、屈折）は、フェルマーの原理「光は可能なすべての経路のなかで最短時間で行ける経路を通ってくる」にまとめることができました。自然がなぜそのようなことをしているのかを説明できる人は誰もいません。でも、自然はそのようになっているのです。不思議なことですよね。

最後にもうひとつ、フェルマーの原理の適用例をお目にかけましょう。

皆さんは、光は直進するということを、経験的に知っていますよね。しかし、重力が強く働くところでは、光は重力によって曲げられてしまうことがわかっています。このことを最初に考えたのは、アインシュタインでした(一般相対性理論と呼ばれます)。でも光は重さを持っていないのですから、「重力によって引き寄せられる」という言葉は正確ではありません。本当のところは、次のようなことが起こっているのです。

まず質量が存在すると、回りの空間が曲げられます。「空間が曲がる」なんて、頭でとても想像がつきませんから、例として2次元の空間を考えましょう。質量が何もない時は、空間は平坦なもの、つまり平面になります。ところが質量が存在すると、質量の回りの空間は曲げられて、質量付近が凹んで曲面になります。そして(ここが重要なことですが)このような曲がった空間においても、「フェルマーの原理」が使えるのです! つまり、この曲がった空間で2点を結ぶ可能なあらゆる経路のうち最短時間で行けるものを、光は選んでやってくるのです。平面上では2点を結ぶ直線が最短経路となりますが、空間が曲がってしまっている場合は、光は曲面上を進むので、最短経路は曲線になります。よって、光は見かけ上、重力に引かれて曲げられるように見えるのです。

アインシュタインは、光の性質が空間の性質と密接に関係していることを、早い時期から察知していました。そして、フェルマーの原理の重要性も良く理解していたのです。もし、フェルマーの原理が知られていなかったなら、この偉大な発見はもっと遅れていたかもしれません。光が太陽の重力によって曲げられるのを観測したのは、アインシュタインが一般相対性理論を発表して、数年後のことでした。

たった一つの原理が、さまざまな物理現象を鮮やかに説明することが、物理ではしばしば起こります。これがが物理の面白さの一つなのです。ここで紹介した光の性質は、その代表的な例であるといえます。

次回は、力学における最小化の問題を考えてみましょう。