2019年の阪大入試（理系）第4問（1）をめちゃくちゃ遠回りして解くその1

1078

概要

皆さんは2019年の阪大前期日程の2次試験で出題された次の問題を知っていますか？

下の図のように, $\dfrac{1}{1}$から始めて分数$\dfrac{p}{q}$に$\dfrac{p}{p+q}$と$\dfrac{p+q}{q}$がつながっている樹形図を考える．このとき，この樹形図に現れる分数は全て既約分数である．
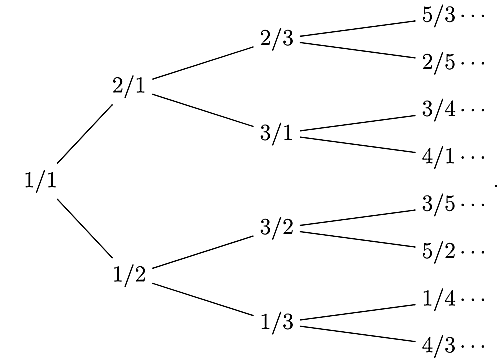calkin-wilf

入試問題としてはあまり見ない傾向の問題だと思われます．面白いですね．
この問題を解くこと自体は，得意な人にとってはそんなに難しくはないと思います．今回は，この問題を敢えて最短ルートで解かずに，このツリーの背景にある興味深い数学的現象を経由して証明を与えたいと思います．かなり長いので何回かに分割して執筆する予定です．この話の内容は論文[Gyo20]に基づいているので，僕の執筆が待ちきれない人は（そんな人いるのかわからないけど）この論文を参照してもらえるとありがたいです．
ちなみに，このツリーにはCalkin-Wilfツリーという名前がついています．その名の通り，CalkinさんとWilfさんが2000年に[CW00]の中で導入しました．素朴な定義の割に結構新しい概念なんですね．今回は右上右下の位置関係はあまり気にしません．$\dfrac{p}{q}$に$\dfrac{p}{p+q}$と$\dfrac{p+q}{q}$が繋がってるということだけ気にしておけばOKです．

Stern-Brocotツリー

まず，Calkin-Wilfツリーによく似たStern-Brocotツリーというツリーを導入します．いろんな定義がありますが，今回は位置関係までガッチガチに定めずに，どの分数にどの分数がつながっているかだけを定める定義を採用したいと思います．そのための準備として，まずFareyトリプルツリーを定義します．

Fareyトリプルツリー

$\left(\dfrac{0}{1},\dfrac{1}{0},\dfrac{1}{1}\right)$から始めて，$\left(\dfrac{a}{b},\dfrac{c}{d},\dfrac{e}{f}\right)$に繋がる2つの三つ組を以下のルールで定める：真ん中の大きさの分数が (i) $\dfrac{a}{b}$, (ii) $\dfrac{c}{d}$, (iii)$\dfrac{e}{f}$であるとき，それぞれ
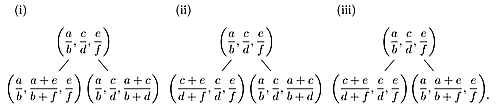Fareytriple
でつながっているとする．このような樹形図を，Fareyトリプルツリーという．

要は，3つ組のうち，最大の分数か最小の分数のどちらかを，残りの2つの分数の分母同士分子同士を足し算した分数に取り替えましょうという話ですね．分数覚えたての小学生がついやってしまう，「間違った分数の足し算」です．$\dfrac{1}{0}$というなにやらちょっといろいろマズそうな分数が登場しておりますが，ここではあまり深い事は考えずに$\infty$の既約分数表示だと思ってもらえばいいです．数としての大きさは，他のどんな分数よりも大きいとします．このツリーの最初の方はこんな感じになってます．
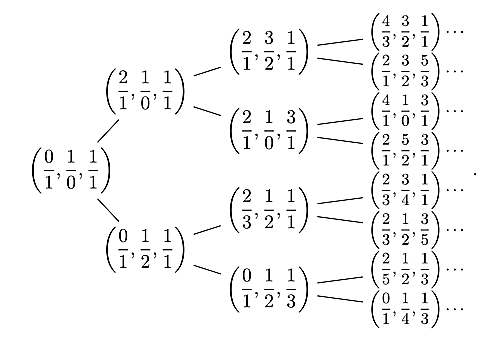Fareytripleinitial
これを使ってStern-Brocotツリーを定めましょう．

Stern-Brocotツリー

Fareyトリプルツリーの各頂点を，その3つ組のうち真ん中の大きさの分数で置き換えたツリーをStern-Brocotツリーという．

Stern-Brocotツリーの最初の方はこんな感じ．
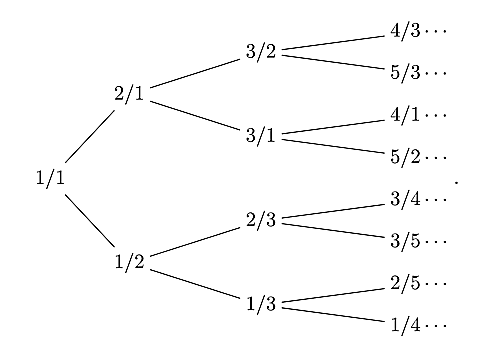stern-brocot
なにやら雰囲気はCalkin-Wilfツリーに似ていますがちょっと違いますね．こちらのルーツはCalkin-Wilfツリーが誕生するよりももっと昔，1800年代まで遡ります．あまり詳しくは知らないのですがSternさんの研究[Ste58]やBrocotさんの研究[Bro62]に因んで名付けられたそうです．

定理1の証明の方針

さて，この記事はひとまず主題である定理1の基本方針だけ述べて締めることにしましょう．まず，当面は以下の事実を証明することを目指します．

Stern-Brocotツリーの各頂点の分数は全て既約分数である．

これを示した後で，次の事実を示します．これがこのシリーズの肝と言ってもよい超重要な部分です．

Stern-BrocotツリーとCalkin-Wilfツリーは双対的な関係にあるツリーである．

なんのこっちゃという感じですね．とりあえず，さっき紹介したStern-BrocotツリーとCalkin-Wilfツリーはなんかいい感じの対になっていて，この事実とStern-Brocotツリーの各頂点が既約分数であることを使って最終的に定理1を示そうという方針だということは覚えておいてください．
ここで，この双対性を与えるのに必要なツールを一つ紹介しておきたいと思います．それがこちら．
torus torus
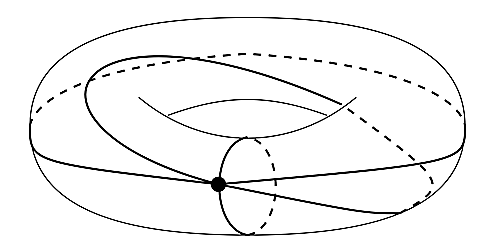
はい，謎は深まるばかりですね．これはトーラス（ドーナツの表面）に1点印をつけて，この点を基準としてトーラスの表面を三角形に分割した図です．まだ何を言っているかわからないかもしれません．そもそも頂点が1つしかないのに三角形も何もありゃしないじゃないかという方もいると思います．ていうか我々はそもそも分数の樹形図の話をしていたんじゃないのか！？これらの話は，順を追って次回以降の記事で解説していこうと思います．ということで，謎に次ぐ謎を残したところで，この記事を終わりにしたいと思います．ここまでお読みいただきありがとうございました．

次の記事： 2019年の阪大入試（理系）第4問（1）をめちゃくちゃ遠回りして解くその2

参考文献

[Bro62] A. Brocot, Calcul des rouages par approximation: nouvelle méthode, Brocot, 1862
[CW00] N. Calkin and H. S. Wilf, Recounting the rationals, Amer. Math. Monthly 107 (2000), no.4, 360–363.
[Gyo20] Y. Gyoda, Cluster duality between Calkin-Wilf tree and Stern-Brocot tree, 2020. preprint, arXiv:2009.06473 [math.NT]
[Ste58] M. S. Stern, Üver eine zahlenteoretische funktion, J. Reine Angew. Math. 55(1858), 193–220