二重根号に関する不思議な等式

二重根号に関する初歩的な知識

二重根号とは？

とは、根号の中に根号がネストされて2重になった構造のことである。二重根号の例として、$\sqrt{1+\sqrt{2}}$や$\sqrt[3]{4+\sqrt[5]{6}+\sqrt[7]{89}}$などが挙げられる。($\sqrt[n]{m}$で$m$の正の$n$乗根、つまり$n$乗して$m$になる正の数を表す。)
　また、根号が3重にネストされた$\sqrt{1+\sqrt{2+\sqrt[3]{4}}}$のような式は三重根号と呼ばれ、より一般に、根号が$n$重にネストされた式を$n$重根号と呼ぶ。2重以上の根号をまとめて多重根号と表現することもある。

多重根号の中には、等式$\sqrt{a^2}=|a|$を用いてネストの回数を減らすことができるものがある。例えば、
$$ \left(1+\sqrt{3}\right)^2=4+2\sqrt{3}$$であるから、以下の等式が成立する。
$$\begin{eqnarray} \sqrt{2+\sqrt{3}}=\sqrt{\frac{4+2\sqrt{3}}{2}}=\frac{\sqrt{\left(1+\sqrt{3}\right)^2}}{\sqrt{2}}=\frac{1+\sqrt{3}}{\sqrt{2}}\end{eqnarray}$$　このようにしてネストの回数を減らすことをディネスティングと呼ぶ。上の例のように、ディネスティングの結果根号のネストが解消される場合は多重根号を外す(一重化、脱多重化)という表現も存在する。二重根号はディネスティングすると必ず一重化される。
　ただし、ディネスティングはすべての多重根号に対して行えるわけではなく、さらにディネスティングの操作は概して非常に困難である。具体例を挙げると、$\sqrt{5+2\sqrt{5}}$はディネスティングができない。
$$ \\ $$

二重根号を外すテクニック

$$ \left(\sqrt{a}\pm\sqrt{b}\right)^2=(a+b)\pm 2\sqrt{ab} \,\,\,\,\,\, (a\geq b\geq 0)$$
という等式を考えると、二重根号$\sqrt{s\pm 2\sqrt{t}}$について、$s=a+b$、$t=ab$となるような$a$、$b$を求められれば、二重根号をディネスティングすることができるとわかる。このような$a$、$b$は2次方程式を解くことによって求められ、
$$\begin{eqnarray} a=\frac{s+\sqrt{s^2-4t}}{2}\, , \; b=\frac{s-\sqrt{s^2-4t}}{2}\end{eqnarray}$$となる。
　ただし、$a$、$b$が求められることとディネスティングができることは同値ではない。先に挙げた$\sqrt{5+2\sqrt{5}}$の場合を考えると、上の式で$s=t=5$として、
$$\begin{eqnarray} a=\frac{5+\sqrt{5}}{2}\, , \; b=\frac{5-\sqrt{5}}{2}\end{eqnarray}$$が得られるが、これを用いて書き直しても
$$\begin{eqnarray} \sqrt{5+2\sqrt{5}}=\frac{\sqrt{5+\sqrt{5}}+\sqrt{5-\sqrt{5}}}{\sqrt{2}}\end{eqnarray}$$
となってしまい、結局根号は2重のままである。即ち、$s^2-4t$が有理数の平方となる場合にしかこの方法は適用できない。

二重根号の有名な式

有名な式を列挙する。
$$ \sqrt{4+3\sqrt{2}}=\sqrt[4]{2}+\sqrt[4]{8}$$　この等式は、左辺に2乗根しか登場しないにもかかわらず右辺に4乗根が登場する点で有名である。
$$\begin{eqnarray} \sqrt[3]{\sqrt[3]{2}-1}=\frac{1-\sqrt[3]{2}+\sqrt[3]{4}}{\sqrt[3]{9}}\end{eqnarray}$$　この等式はインドの数学者、シュリニヴァーサ・ラマヌジャンが発見したとされる。ラマヌジャンはこの他にも多くの発見をしているので、興味があれば調べてみるとよい。
$$ \sqrt{10+2\sqrt{6}+2\sqrt{10}+2\sqrt{15}}=\sqrt{2}+\sqrt{3}+\sqrt{5}$$　この等式はインドの数学者兼天文学者、バースカラ2世が発見したとされる。誰でも見つけられる平易な等式である。
　以上の等式が成立することは、右辺をそれぞれ2乗、3乗、2乗することで確かめられる。

二重根号の不思議な等式とその応用

以下は、研究によって筆者が発見した等式である。(先行研究などを御存知の方がいらっしゃったら、コメントで御教授ねがいたい。)

一見複雑そうな見た目をしているが、その本質は驚くほど単純である。まずは2つの式に$x=0$を代入してみよう。
$$\begin{eqnarray} &&\sqrt{18+8\sqrt{2}}&=&\left(\sqrt{2}+1\right)\left(\sqrt{2}\right)+2&=&4+\sqrt{2} \\ &&\sqrt{18+8\sqrt{2}+2\sqrt{5}}&=&\left(\sqrt{2}+1\right)\left(\sqrt{5}+1\right)-2&=&\sqrt{2}+\sqrt{5}+\sqrt{10}-1 \end{eqnarray}$$　次に、$x=1$を代入してみる。
$$\begin{eqnarray} &&\sqrt{28+10\sqrt{3}}&=&\left(\sqrt{3}+1\right)\left(\sqrt{3}\right)+2&=&5+\sqrt{3} \\ &&\sqrt{28+10\sqrt{3}+4\sqrt{6}}&=&\left(\sqrt{3}+1\right)\left(\sqrt{6}+1\right)-2&=&3\sqrt{2}+\sqrt{3}+\sqrt{6}-1 \end{eqnarray}$$　お気付きだろうか。左辺と右辺の一部が、上下の式で共通している。加えて、下の式の左辺には$x+1$から$x+6$までの整数係数の1次式がすべて1回ずつ登場する。
　
　さらに、以下の関係も成り立っている。

$({\rm B'})$、$({\rm B'''})$の右辺に絶対値記号が付いているのは、その中身が負になりうるためである。(等式$\sqrt{a^2}=|a|$を参照)
　これらを用いると、以下のように、より不思議な等式を導くことも可能である。

※$({\rm P})$、$({\rm Q})$について、根号の中身を「無理式の2乗+根号」という形に整理した。これは$({\rm A})$、$({\rm A'})$の両辺を2乗したものをそれぞれ$({\rm B})$、$({\rm B'})$に代入することで得られる。

余談

上の等式のいずれにも当てはまらない二重根号$\sqrt{\left(7+\sqrt{2}\right)^2+4\sqrt{15}}$について、
$$ \sqrt{\left(7+\sqrt{2}\right)^2+4\sqrt{15}}=2\sqrt{3}-\sqrt{5}+2\sqrt{6}+\sqrt{10}$$のようにディネスティングが可能である。根号の中身が「無理式の2乗+根号」である二乗根号のうち、上の等式に従っていないものについては今後の研究課題としたい。
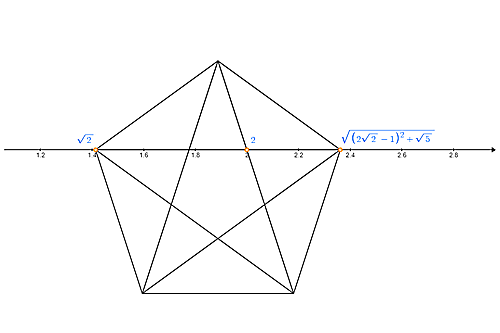
　なお、$\displaystyle{\frac{1+\sqrt{5}}{2}}$は一辺が$1$の正五角形の対角線の長さであるから(証明略)、$({\rm P})$より下図の関係が明らかになる。

pentagon_root2