気ままな物理の小文（２）ハミルトンの原理：力学の中に潜む最適化問題

はじめに

我々にとって過去と未来は全く違うものです。過去の記憶はありますが、未来に起きることを知ることができません。10分前のことは良く覚えていても、10分後に何が起こるかはわかりません。それでも「もしも未来が予測できたら」と考えてみたくなるものです。サイエンスフィクション(SF)の世界では、そのような「もしも」はよく取り上げられる題材です。SF小説の巨匠であるフィリップ・K・ディックは、短篇小説「ゴールデンマン」のなかでそのような「もしも」を実現してみせました。主人公のクリスは、未来を予知する能力を備えた人間の変種（ミュータント）であり、その能力ゆえに国家機構から追われる身となります。彼は自分の行動によってひきおこされるあらゆる可能な未来を見ることができ、その中から自分にとってもっとも適した未来を選ぶことができます。

しかしそれはSFの世界の中だけの話ではなく、物理現象の中にも「ありとあらゆる仮想未来のなかで最適なものを選んでいる」ようにみえるものがあります。その一例は前回お話した、光学におけるフェルマーの原理なのですが、もっと身近な例が存在します。これが今回のテーマです。

力学における最小化問題

重力のもとでの物体の運動を考えてみましょう。物体を時刻$t=0$に初速度$v_0$で鉛直上方へ投げ上げたとします。物体は図1のように初めのうちは、上向きに動きますが、だんだんと減速していってどこかで折り返し、その後は落下を始めます。図1のように鉛直上向きに座標$x$をとり、物体の位置を座標$x$で表わすことにしましょう。ただし物体の始めの位置を$x=0$とします。横軸を$t$ 、縦軸を$x$として物体の運動の様子をグラフで表わすことにすると、図1のようになります。実験を繰り返して物体の運動を解析すると、時刻$t$での物体の位置は、
\begin{equation} x(t)=v_0 t - \frac{1}{2} g t^2 \ \ \cdots \ \ (1) \end{equation}
という$t$の二次関数で書けることがわかります（$g$は重力加速度）。ここまでは、高校の物理の範囲内です。

さて、この問題を全く違う視点でとらえてみることにしましょう。物体は時刻$t=0$に位置$x=0$にあります。さらに物体が時刻$t=t_1$に位置$x=x_1$を通過したとしましょう。このとき、物体は$x$-$t$グラフ上で二点${\rm O}(0,0)$, ${\rm A}(x_1,t_1)$を通らなくてはいけません。ところでO, A を通るような曲線$x(t)$はいろいろあります。頭のなかでは図2のように、O, Aの間をさまざまな形の曲線でつなぐことができます。しかし実際におこる物体の運動を表わす曲線は、もちろんただ一つ（式(1)で表される運動）です。では、実際に時刻tでの物体の位置$x(t)$のグラフの形はどうやって決まるのでしょうか。

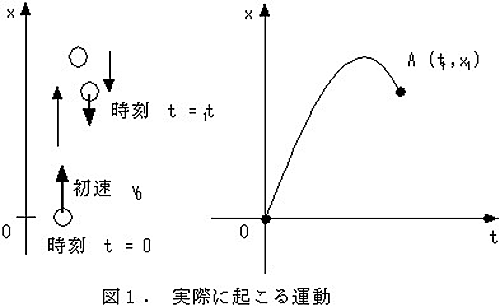fig2-1

ここまでくると、物体の運動の決定（つまり、位置$x(t)$の決定）が、先月解説した光の経路の決定と、とても似ていることが分かるでしょう。光の場合は、可能なあらゆる経路のうちで到達時間を最小にするような経路を選びました。物体の運動も、あらゆる可能なグラフ$x(t)$のうち何かを最小にするような曲線を選んでいるんでしょうか？。
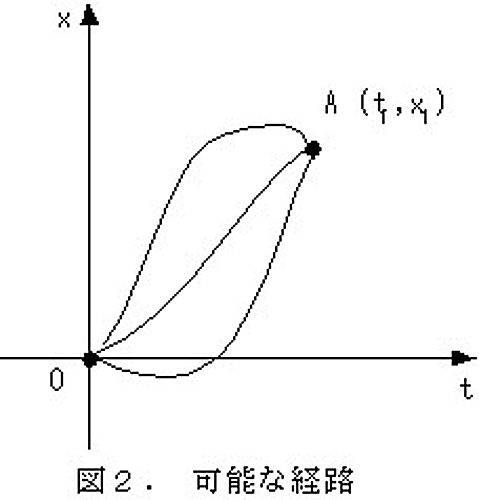fig2-2
この問いに対する答えは、19世紀の物理学者ハミルトンによって次のように与えられました。

ここで$m$は物体の質量、$v=dx/dt$は物体の速度です。急に積分が出てきたので、引いてしまうかもしれませんが、大体の感じをつかむだけなら、ある程度簡単にできます。

まず、物体の運動$x(t)$が決まれば、積分量$S$はただ一つに決まることに注意しましょう。逆に$x(t)$のグラフの形を変化させれば積分量$S$の値もどんどん変化します。変化します。（これはちょうど、経路の長さは経路の形が決まるとただ1つに決まり、経路の形を変えていくと経路の長さが変化することと、とてもよく似ています。）

次に、被積分関数が、運動エネルギーと位置エネルギーの差の形をしていることに注意しましょう。積分量$S$を最小にするには、できるだけ運動エネルギーを小さく、位置エネルギーを大きくしなくてはいけません。

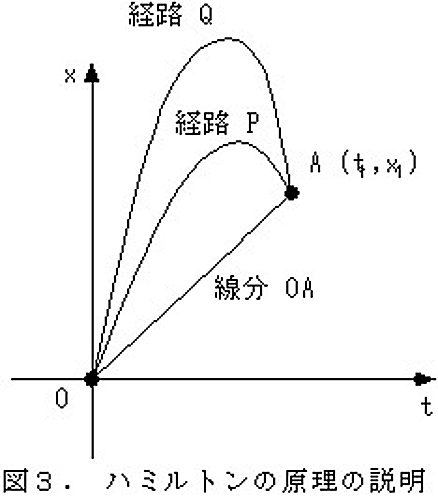fig2-3

これだけ指摘しておいて、実際の物体の放物運動がハミルトンの原理からどのように説明されるかを説明してみましょう。図3を見てください。まず$x$-$t$グラフ上の二点${\rm O}(0,0)$と${\rm A}(t_1,x_1)$を結ぶ線分OAを考えて見ましょう。とりあえず頭のなかでは、このような経路を考えることができるし、経路を決めたので積分量$S$も計算できます。しかしこの経路は積分量$S$を最小にしません。なぜなら、図3のようにちょっと経路を上にずらして経路Pとすれば、その分位置エネルギーを大きくすることができるからです。そうすれば、式(2)の積分の第2項が大きくなって、積分量$S$の値を小さくできます。

しかしどんどん上にずらせばよいというものではありません。例えば経路Qのように極端に経路を上にずらすと曲線$x(t)$の傾き$dx/dt$の大きさが、かなり大きくなります。この傾きが物体の速度$v$にあたりますから、それによって運動エネルギー$mv^2/2$が大きくなります。すると積分の第1項が大きくなって、積分量$S$も大きくなってしまいます。「過ぎたるは及ばざるがごとし」なのです。

さてこのように考えていくと、うまく位置エネルギーを大きく、かつ運動エネルギーがそれほど大きくならないようにして、積分量$S$を最小にする経路$x(t)$が存在しそうですよね。まさにその$S$を最小にする経路$x(t)$が実際に実現される経路なのです！

実際に計算してみる

ハミルトンの原理が本当に正しく物体の運動を記述するかどうかを、確かめてみましょう。経路$x(t)$に対する積分量$S$の値を$S[x(t)]$と表わすことにします。（この書き方には「経路の形$x(t)$が決まると$S$の値がただ一つに定まる」という気持ちがこめられています。）この積分量$S$を最小にするような経路を求めてみましょう。その求め方は変分法と呼ばれています。

fig2-4

まず適当な経路$x(t)$をとります。次に経路を図4のように$x(t)$から$x(t)+h(t)$とわずかにずらしてみましょう。ここで$h(t)$は$t$の関数で、経路の微小なずれを表わす関数です。ただし、経路の両端の座標${\rm O}(0,0)$, ${\rm A}(t_1,x_1)$はずらしてはいけないので、
\begin{equation} h(0) = h(t_1) = 0 \ \ \cdots \ \ (3) \end{equation}
が成り立つ必要があります。ここで、経路を$x(t)$から$x(t) + h(t)$に変化させたときの$S$の値の変化を考えてみます。
\begin{eqnarray} S &=& S[x(t)+h(t)]-S[x(t)] \\ &=& \int_0^{t_1} \left[\frac12 m \left(\frac{dx}{dt} + \frac{dh}{dt}\right)^2 -mg(x+h)\right] dt -\int_0^{t_1} \left[ \frac12 m \left(\frac{dx}{dt}\right)^2 -mgx \right]dt \\ &=& \int_0^{t_1} \left( m \frac{dx}{dt} \frac{dh}{dt} - mgh \right) dt \ \ \cdots \ \ (4) \end{eqnarray}
最後の変形では経路のずれ$h(t)$は十分小さいとして、$(dh/dt)^2$の項は、無視しました。積分の第１項は、部分積分によってさらに変形することができます。
\begin{equation} \int_0^{t_1} \left( m\frac{dx}{dt} \frac{dh}{dt}\right) dt = \left[m \frac{dx}{dt} h \right]_0^{t_1} - \int_0^{t_1}\left( m \frac{d^2x}{dt^2} h \right) dt \end{equation}
右辺の第１項は、$h(0)=h(t_1)=0$より消えてしまいます。よって式(4)は結局、
\begin{equation} \Delta S = \int_0^{t_1} \left(-m\frac{d^2 x}{dt^2} -mg\right) h\, dt\ \ \cdots \ \ (5) \end{equation}
変形されます。

この式の意味を考えて見ましょう。今、経路$x(t)$から経路$x(t)+h(t)$にわずかにずらしたときに、$S$の値が減少したとしましょう。つまり、$\Delta S < 0$だったとします。このときは、経路$x(t)$は$S$を最小にしていません。ずらした経路$x(t)+h(t)$の方が、$S$の値が小さいからです。

逆に経路$x(t)$から経路$x(t)+h(t)$にずらしたときに$S$の値が増加した（$\Delta S>0$）としましょう。この場合も経路$x(t)$は$S$の値を最小にしていません。なぜなら、経路を逆の方向にずらせば、$S$の値は減少するからです。具体的には、経路$x(t)$に対して経路$x(t)-h(t)$を作ってやったほうが$S$の値が小さくなります。これを式の上で確かめるのは簡単です。経路のずれ$h(t)$と$S$の値の変化$\Delta S$との間には、式(5)の関係があります。ある経路のずれ$h(t)$に対して、$S$が増加（$\Delta S>0$）したとしましょう。式(5)の被積分関数は、$h(t)$に比例していますから、$h(t)$を$-h(t)$に置き換えると$\Delta S$の符号はひっくりかえります。よって、経路のずれ$-h(t)$に対して$\Delta S<0$となり、$S$の値は減少します。

以上のことから、経路$x(t)$が積分量$S$を最小にするためには任意の経路のずれ$h(t)$にたいして$\Delta S >0$ でも$\Delta S < 0$でもだめで、
\begin{equation} \Delta S = \int_0^{t_1}\left(-m\frac{d^2x}{dt^2}-mg \right)h(t)\,dt = 0 \end{equation}
が成立しなくてはならないことが、分かります。さらに、どのような経路のずれ$h(t)$に対してもこの式が成り立つためには、このとき$h(t)$の前にかかっている式は常に0にならなければいけないことが証明できます。結局、
\begin{equation} m\frac{d^2x}{dt^2}=-mg \end{equation}
が成り立たないといけません。これはまさしく運動方程式です！この式を2回積分して、初期条件（$t=0$で$x=0$, $v=v_0$）を用いて積分定数を決めると、式(1)が導かれます。こうして、ハミルトンの原理は正しく現象を記述することがわかりました。

ここまでの話で興味が湧いた人は、ぜひ「ファインマン物理学」第3巻（岩波書店）を読んでみてください。もっと詳しく、情熱的な解説があります。

終わりに

ちょっと身の回りの適当なものをとって投げてみて下さい。放物線を描いて運動しますよね。実際に起こる物体の運動は、あなたが見た運動ただ一つです。ここでちょっと想像してみて下さい。物体は投げ出された瞬間から着地するまで、あらゆる運動の可能性があります。なかにはとんでもない（超常現象のような）運動だって含まれています。投げ出した瞬間には物体には無数の未来があるわけです。ところが実際に起こる未来ただ一つで、ここまで説明してきたハミルトンの原理に従えば、その運動は積分量$S$を最小にしています。ですからこんな見方が可能です。「物体は未来のあらゆる可能な運動を試してみて、その一つ一つの未来に対して積分量$S$の値を計算し、そのなか$S$を最小にするやつを選び出して未来を決定している！」冒頭でお話したディックの小説での話と似た現象が身の回りでも起こっている、と見ることも可能なのです。

物体が本当に可能な未来をすべて試してみているのか、本当のところは良くわかりません。そこは人の見方によりけりでしょう。でもこんな考え方で物体の運動が説明できてしまうところがとても魅力的だと思いませんか？ハミルトンのまえにこの原理の原型を発見したモーペルテュイは、この原理に基づいて、神の存在を証明しようとしました。気持ちはわからないでもないですよね。

このような「何かを最大にしている」という考え方は、気体分子運動論でも大活躍します。気体分子の速度分布を求めるときに、実は「場合の数が最大になるべし」という法則を使うとマックスウェルの速度分布則が導出できたりします。ほかにもいろいろな場面で「何かを最大にしている」ということがうまく使われています。経済学や数理工学、統計学などがそうですね。さらに最近流行りの機械学習やAIも「ある量を最大にすべし」という定式化をよく行います。

ところで、人間の行動原理にも、同じようなことがあるでしょうか？その場合、一体何を最大にしようとして行動しているのでしょうか。あなたの行動原理は？まぁ、そんなことを思い浮かべながら、この小文を閉じることにしましょう。